随着未来无线通信多媒体和交互式应用业务的深入推广，移动用户对通信系统的高传输率和可靠性的需求越来越高. MIMO中继通信系统可充分利用时间、空间、频率及协同中继等分集技术，进一步提高通信系统的覆盖范围和信道容量^[1-2].

在MIMO中继通信系统中，无论是发射端功率优化、中继节点选择或是符号检测，多是以已知信道矩阵为前提的^[3].因此对MIMO中继系统信道估计的研究已引起了越来越多的重视.传统方法通过监督训练序列来得到信道矩阵，此时，信道估计是被监督的，或者说是非盲的.一方面，训练序列的使用降低了频谱利用效率，另一方面，如果信道系数变化较快时，难以估计出较为准确的CSI.盲接收则在接收端不需要任何信息的情况下，就能估计出信道信息和符号.而半盲接收仅要求已知编码矩阵和中继增益矩阵，因此可提升系统的频谱利用效率.

在监督估计算法方面，Rong提出了监督序列的双线性交替最小二乘方法(Bilinear Alternating Least Square，BALS)来估计中继单向AF(Amplify and Forward)系统的信道^[4].该算法由源节点向中继节点发送接收端已知的正交训练序列，中继节点采用满秩的增益矩阵对信号进行放大转发，接收到的信号满足PARAFAC模型，可利用基于交替最小二乘算法对信道矩阵进行估计. Lioliou提出了LS-SVD(Least-Square Singular Value Decomposition)估计算法，该算法考虑接收信号的模3展开，利用最小二乘与奇异值相结合的方法进行信道估计^[5].值得一提的是，有文献表明这两种算法性能相同^[6].

在半盲估计算法方面，Ximenes提出基于PARATUCK2模型的半盲估计算法，该算法在信源端利用KRST(Khatri-Rao Space Time)编码，中继端采用放大转发策略，接收端利用最小二乘算法进行信道估计^[6]. Ximenes提出基于嵌套NP(Nested PARAFAC)张量模型的半盲接收算法^[7]，该算法在信源端及中继端均利用KRST编码提高分集和复用增益，在接收端利用最小二乘算法方法进行信道和符号估计.由于接收信号为四维张量，每次迭代过程中涉及多次求逆运算，计算复杂度较高.文献[9]提出基于DKRF(Double Khatri-Rao Factorization)的接收算法，相比交替最小二乘算法，该算法避免迭代操作，在一定程度上降低计算复杂度，但唯一性条件要求比较严苛.在降低复杂度方面，有关张量分解算法已提出了许多优化的低复杂度非线性求解算法，如NLS、部分最小二乘(Partial Least Square，PLS)等，但相对于ALS，在多峰存在情况下，往往只能局部收敛^[8].

可看出，目前在单向双跳MIMO中继系统中，基于张量分解的半盲估计大都采用确定性的算法.当研究信道的统计特性已知的情况下(如瑞利衰落信道)，确定性算法无法引入信道的先验统计特性.因此需建立信道估计的概率模型.常见的概率模型有最大似然估计(Maximum Likelihood，ML)、期望最大(Expectation Maximum，EM)、马尔科夫链蒙特卡洛(Markov Chain Monte Carlo，MCMC)等^[10-11]. EM和ML都无法利用已有的先验信息，而MCMC虽可利用已有先验信息，但收敛速度慢，且马尔科夫链的收敛性难以保证，难以在实际工程中应用和推广^[12].近年来，一种能适应张量数据环境，以较少运算量进行参数估计的变分近似方法逐渐被关注. Attias最早提出了将变分近似思想应用于图像模型的参数推断中^[13]，成为了变分贝叶斯方法的雏形，人们将此方法用于不同领域的参数估计^[14-15]，都取得了不错的成果.相比同样作为逼近方法进行参数估计的MCMC，变分贝叶斯在较好估计精度的前提下有更快的估计速度^[16].

本文基于Attias的变分推断思想，提出了一种贝叶斯结构的MIMO中继系统信道估计算法.该算法基于Nested-PARAFAC张量模型，引入有效精度、噪声精度等隐性超参数，建立信道估计概率模型，在最大化模型证据意义上，采用变分贝叶斯推断逼近信道参数及符号矩阵的后验分布.算法可通过隐性超参数将信道先验信息引入到概率模型中，同时计算复杂度与数据维度呈线性关系，明显小于传统NP-ALS算法.仿真结果表明：算法与传统基于监督序列的BALS算法，基于ALS及NLS的算法相比，具有较高的估计性能.

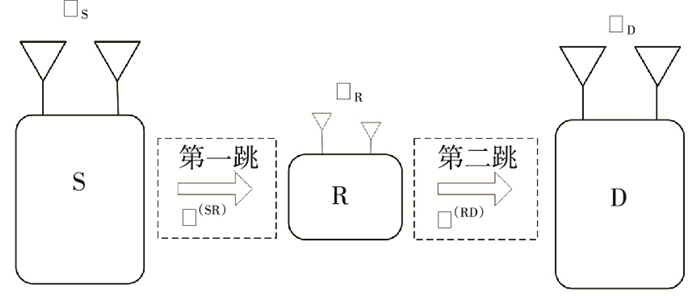
1 系统模型

单向双跳MIMO中继系统的基本框图见图 1^[9].其中S，R，D分别为信源节点，中继节点，目的节点; M_S，M_R，M_D分别表示信源、中继节点及目标节点的天线数量.

源节点至中继节点信道矩阵H^(SR)∈C^M_R×M_S，中继节点至目的节点的信道矩阵H^(RD)∈C^M_D×M_R.传输信道均为平稳瑞利衰落信道.符号矩阵S ∈ C^N_S×M_S，其中N_S为传输符号数.整个传输过程分为两跳：第一跳，每个源天线经过空时KRST编码后，向中继节点发送信号; 第二跳，源节点保持静默，中继节点将接收到的信号进行放大转发至目的节点.

假定源节点和中继节点的天线是独立的(在没有干扰的情况下)，节点可看作是多天线的单个终端，或者是单天线的多个终端.图 1所示系统能适用于很多实际需求.比如：M_S $ \gg $ M_R的场合对应于蜂窝移动通信系统，它是一种高度集中的中继网络，大量的用户共享几个转发器，以使信息发送至基站.而M_S $ \ll $ M_R适用于Ad hoc网络，点对点的通信会经过多个中继节点.在文献[5]的基础上，对信息源模型和中继链路模型进行建模.

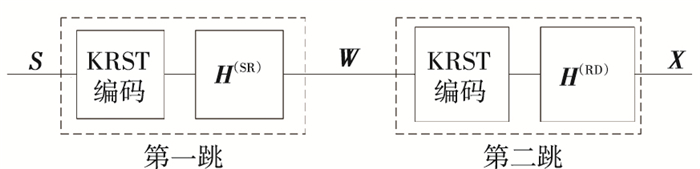
NP-AF方案基本原理见图 2.在第一跳时，利用编码矩阵对符号矩阵S进行KRST编码，编码后信号经SR信道达到中继节点，此时信号为W∈C^M_R×PN_S; 第二跳时，中继端利用编码矩阵G对信号W进行KRST编码，编码后信号经RD信号到达目的节点，此时接收信号矩阵X∈C^M_D×JPN_S可表示为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{H}}^{\left( {{\rm{RD}}} \right)}}{{\left( {{\mathit{\boldsymbol{W}}_{P{N_{\rm{S}}} \times {M_{\rm{R}}}}} \odot G} \right)}^{\rm{T}}} = }\\ {{\mathit{\boldsymbol{H}}^{\left( {{\rm{RD}}} \right)}}{{\left( {\left( {\mathit{\boldsymbol{S}} \odot \mathit{\boldsymbol{C}}} \right){{\left( {{\mathit{\boldsymbol{H}}^{\left( {{\rm{SR}}} \right)}}} \right)}^{\rm{T}}} \odot G} \right)}^{\rm{T}}}.} \end{array} $

(1)

式中：J和P为编码矩阵 G 和编码矩阵 C 的编码长度，T表示矩阵的转置，⊙为Khatri-Rao算子.值得一提的是，为保证系统分解的唯一性，通常要求编码矩阵 C ，中继矩阵 G 为列满秩，信号矩阵 S 不包含零列，且信道矩阵为强散射条件下的瑞利信道，其元服从连续复高斯分布.

式(1)可看作是四阶张量 X ∈C^{M_D×J×N_S×P}的模1展开.其它展开形式见文献[5].

2 基于变分贝叶斯的半盲信道估计 2.1 基本模型

假设 Y 为四阶张量数据，其维度为M_D×J×N_S×P，它是发送数据夹杂有噪声的观测张量，即 Y= X + ε，其中 X 代表真实的接收数据张量，ε 为加性高斯白噪声.

对于四阶张量 X ，其Nested-PARAFAC分解的因子矩阵可表示为

$ \mathit{\boldsymbol{X}} = 〖 {{\mathit{\boldsymbol{H}}^{\left( {{\rm{RD}}} \right)}},{\mathit{\boldsymbol{H}}^{\left( {{\rm{SR}}} \right)}},\mathit{\boldsymbol{G}},\mathit{\boldsymbol{S}},\mathit{\boldsymbol{C}}} 〗. $

式中：增益矩阵 G、编码矩阵 C为已知，H^(SR)矩阵的维度为M_R×M_S，H^(RD)矩阵的维度为M_D×M_R，S矩阵的维度为N_S×M_S.

构建在概率框架下的张量分解模型，需基于一定的假设引入以下模型.一般地，观测张量Y的似然函数可表示为

$ p\left( {\mathit{\boldsymbol{Y}}\left| {\left\{ {{\mathit{\boldsymbol{H}}^{\left( {{\rm{RD}}} \right)}},{\mathit{\boldsymbol{H}}^{\left( {{\rm{SR}}} \right)}},\mathit{\boldsymbol{S}}} \right\},\tau } \right.} \right), $

(2)

式中τ代表噪声精度.式(2)可表示为一系列高斯分布函数乘积，表明接收张量的元素由多个因子的行向量产生，并受噪声精度的影响.进一步地，为有效利用因子矩阵的先验信息，引入有效精度的后验分布

$ \begin{array}{*{20}{c}} {p\left( {\left. {\left\{ {{\mathit{\boldsymbol{H}}^{\left( {{\rm{RD}}} \right)}},{\mathit{\boldsymbol{H}}^{\left( {{\rm{SR}}} \right)}},\mathit{\boldsymbol{S}}} \right\}} \right|\lambda } \right) = }\\ {\prod\limits_{{i_n} = 1}^{{I_{N}}} {N\left( {\left\{ {h_{{i_n}}^{\left( {{\rm{SR}}} \right)},h_{{i_n}}^{\left( {{\rm{RD}}} \right)},{s_{{i_n}}}} \right\}\left| 0 \right.,{\Lambda ^{ - 1}}} \right)} ,}\\ {p\left( \lambda \right) = \sum\limits_{r = 1}^R {{\rm{Ga}}\left( {{\lambda _r}\left| {{c_0}} \right.,{d_0}} \right)} .} \end{array} $

式中：λ为因子矩阵的有效精度，N(·)为高斯分布，i_n为因子矩阵的行向量个数.随着λ值的增大，p(λ)趋近于0，所分解的因子矩阵有效性降低.而当p(λ)达到最大时，所分解的因子矩阵最有效.另外，R为数据张量的k秩.超参数λ服从独立同分布的Gamma分布Ga(x|a, b)=(b^ax^a－1e^－bx/Γ(a))，其中Γ(a)是Gamma函数. Λ =diag(λ)代表逆协方差矩阵，代表因子矩阵交互关系.

在实际应用中，应结合具体场景指定，这里假定信道为平稳瑞利衰落信道，信道参数服从高斯分布，其有效性由精度参数λ所控制.同时也引入噪声精度的先验信息，可表示为

$ p\left( \tau \right) = {\rm{Ga}}\left( {\tau \left| {a_0^\tau } \right.,b_0^\tau } \right). $

(3)

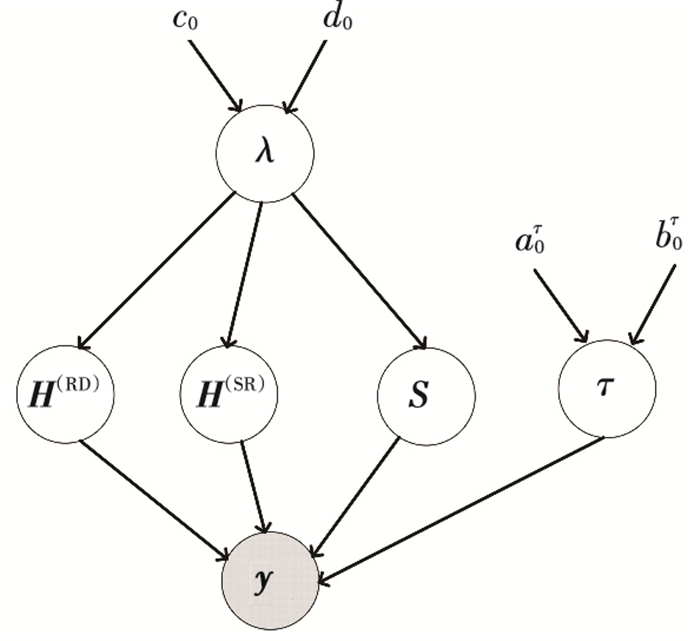
最终Nested-PARAFAC张量分解的概率图模型见图 3.

为简化表示，所有需估计的因子矩阵和超参数表示为 Θ ={ H^(RD), H^(SR), S, λ, τ}，模型的联合概率分布为p(Y, Θ).事实上，可采用最大似然或最大后验等点估计的方式，基于对数联合概率分布计算 Θ 的后验估计.由于联合概率分布函数较为复杂，上述方法难以实现.本文利用变分贝叶斯推断计算 Θ的后验分布，即

$ p\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left| \mathit{\boldsymbol{Y}} \right.} \right) = \left( {p\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }},\mathit{\boldsymbol{Y}}} \right)/\int {p\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }},\mathit{\boldsymbol{Y}}} \right){\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} } \right). $

(4)

2.2 变分贝叶斯估计

当似然分布和先验分布为共轭分布时，后验分布于先验分布为统一分布.基于此，采用变分贝叶斯推断寻找具有因子分解形式的概率分布逼近未知参数的后验概率分布.

寻求q分布来近似真正的后验分布p(Θ | Y)，以使KL距离最小，即

$ \begin{array}{*{20}{c}} {{\rm{KL}}\left( {q\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)\left\| {p\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }},\mathit{\boldsymbol{Y}}} \right)} \right.} \right) = \ln p\left( \mathit{\boldsymbol{Y}} \right) - L\left( q \right),}\\ {L\left( q \right) = \int {q\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)\ln \left\{ {\frac{{p\left( {\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)}}{{q\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)}}} \right\}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} .} \end{array} $

(5)

式中: lnp(Y)代表模型证据(Model Evidence)，是个常量，它的下限为L(q); KL距离的最小值意味着L(q)的最大值.采用平均场近似理论^[17]，假设后验可以分解为

$ q\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right) = \sum\limits_{n = 1}^3 {q\left( {{\mathit{\boldsymbol{A}}^{\left( n \right)}}} \right)q\left( \lambda \right)q\left( \tau \right)} . $

最小化式(4)可得:

$ \ln q\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_k}} \right) = {\mathbb{E}_{\mathit{\Theta \backslash }{\mathit{\Theta }_k}}}\left[ {\ln p\left( {\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)} \right]. $

式中${{\mathbb{E}}_{\mathit{\Theta} \backslash \mathit{\Theta} k}}\left[\cdot \right] $表示关于分布q(Θ _j), $\forall j \ne k $的期望.然后交替优化q(Θ_k)直到收敛.据此，可进一步推导未知参数的更新方式.

1) 因子矩阵的后验分布

由于因子矩阵的推导具有一致性，令$\mathit{\boldsymbol{A}}{\rm{ }} = \left\{ {{\rm{ }}\mathit{\boldsymbol{A}}{^{(n)}}} \right\}_{n = 1}^3 = \{ {\rm{ }}\mathit{\boldsymbol{H}}{^{({\rm{RD}})}}, {\rm{ }}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{}}^{({\rm{SR}})}}, {\rm{ }}\mathit{\boldsymbol{S}}\} $，从图 3中可看出，因子矩阵的推断可利用式(3)中似然函数中观测数据中信息，并结合式(4)先验知识进行推导，可得因子矩阵$ \mathit{\boldsymbol{\tilde A}}{^{(n)}}$的后验参数更新公式

$ \begin{gathered} {{\mathit{\boldsymbol{\tilde A}}}^{\left( n \right)}} = {\mathbb{E}_q}\left[ \tau \right]\left( {{\mathit{\boldsymbol{Y}}_{\left( n \right)}}} \right){\mathbb{E}_q}\left[ {{\mathit{\boldsymbol{A}}^{\left( {\backslash n} \right)}}} \right]{\mathit{\boldsymbol{V}}^{\left( n \right)}}, \hfill \\ {\mathit{\boldsymbol{V}}^{\left( n \right)}} = {\left( {{\mathbb{E}_q}\left[ \tau \right]{\mathbb{E}_q}\left[ {{\mathit{\boldsymbol{A}}^{\left( {\backslash n} \right){\rm{T}}}}{\mathit{\boldsymbol{A}}^{\left( {\backslash n} \right)}}} \right] + {\mathbb{E}_q}\left[ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \right]} \right)^{ - 1}}. \hfill \\ \end{gathered} $

(6)

式中：Y_(n)代表张量数据 Y 的模n矩阵，V⁽ⁿ⁾为辅助矩阵，${{\mathbb{E}}_{q}}\left[\cdot \right] $代表涉及所有变量后验期望.式(6)中 V⁽ⁿ⁾首先利用因子先验${{\mathbb{E}}_{q}}\left[\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \right] $和其它因子矩阵的协方差更新，而这两项的权重通过${{\mathbb{E}}_{q}}\left[\tau \right] $控制调节，因此${{\mathbb{E}}_{q}}\left[\tau \right] $与模型的拟合度相关.相对因子先验信息，较优的拟合应从现有模型中获取更多的信息，较大的观测值意味着模型与隐性因子具有更多相似性.然后$\mathit{\boldsymbol{\tilde A}}{^{(n)}} $通过V⁽ⁿ⁾旋转，并根据模型的拟合度${{\mathbb{E}}_{q}}\left[\tau \right] $进行尺度变换.

2) 超参数λ的后验分布

从图 3可看出，λ的推断可利用因子矩阵的信息和参数的先验信息.假设λ_r, $\forall $ r∈[1, R]的后验是独立的Gamma分布，$ q\left( \lambda \right) = \prod _{r = 1}^R{\rm{Ga}}({\lambda _r}|c_M^r, d_M^r)$，其中R为张量的k秩，$ c_M^r, d_M^r$代表从M个观测值中学习到的后验参数，且能够通过下式更新：

$ \begin{array}{*{20}{c}} {c_M^r = {c_0} + \frac{1}{2}\sum\limits_{n = 1}^N {{I_n}} ,} \\ {d_M^r = {d_0} + \frac{1}{2}\sum\limits_{n = 1}^N {{\mathbb{E}_q}\left[ {\mathit{\boldsymbol{a}}_{ \cdot r}^{\left( n \right)T}\mathit{\boldsymbol{a}}_{ \cdot r}^{\left( n \right)}} \right]} .} \end{array} $

(7)

式(7)中的后验期望项可利用式(6)中的后验参数计算，有

$ {\mathbb{E}_q}\left[ {\mathit{\boldsymbol{a}}_{ \cdot r}^{\left( n \right)T}\mathit{\boldsymbol{a}}_{ \cdot r}^{\left( n \right)}} \right] = \mathit{\boldsymbol{\tilde a}}_{ \cdot r}^{\left( n \right)T}\mathit{\boldsymbol{\tilde a}}_{ \cdot r}^{\left( n \right)} + \sum\nolimits_{{i_n}} {{{\left( {\mathit{\boldsymbol{V}}_{{i_n}}^{\left( n \right)}} \right)}_{rr}}} . $

可进一步简化${\mathit{\boldsymbol{d}}_M} = {\left[{d_M^1, \ldots, d_M^R} \right]^{\rm{T}}} $的计算，有

$ {\mathit{\boldsymbol{d}}_M} = \sum\limits_{n = 1}^N {\left\{ {{\rm{diag}}\left( {{{\mathit{\boldsymbol{\tilde A}}}^{\left( n \right){\rm{T}}}}{{\mathit{\boldsymbol{\tilde A}}}^{\left( n \right)}}} \right) + {{\rm{I}}_n}{\mathit{\boldsymbol{V}}^{\left( n \right)}}} \right\}} . $

3) 超参数τ的后验分布

噪声精度τ的更新可利用超参数信息先验和观测数据联合估计信息推导得出，它的变分后验是Gamma分布，即$q\left( \tau \right) = {\rm{Ga}}(\tau |a_M^\tau, b_M^\tau ) $，其后验参数可利用下式更新

$ \begin{array}{*{20}{c}} {a_M^\tau = a_0^\tau + \frac{M}{2},} \\ {b_M^\tau = b_0^\tau + \frac{1}{2}{\mathbb{E}_q}\left[ {\left\| {\left( {\mathit{\boldsymbol{Y}} - 〖 {{\mathit{\boldsymbol{H}}^{\left( {{\rm{RD}}} \right)}},{\mathit{\boldsymbol{H}}^{\left( {{\rm{SR}}} \right)}},\mathit{\boldsymbol{S}},\mathit{\boldsymbol{G}},\mathit{\boldsymbol{C}}} 〗} \right)}~~ \right\|~_{\rm{F}}^2} \right].} \end{array} $

(8)

式中τ的后验期望可通过${\mathbb{E}_q}\left( \tau \right) = a_M^\tau /b_M^\tau $更新，其中a_M^τ与观测值数量相关，b_M^τ与模型残差的F范数后验相关.

4) 模型证据的下界

可计算式(5)的变分下界.由于在迭代重新估计过程的每一步，这个值是增加的，可以通过监视这个值来检测是否收敛. Log的边缘似然下界可表示为^[18]

$ L\left( q \right) = {\mathbb{E}_q}\left[ {\ln p\left( {\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)} \right] + H\left( {q\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)} \right). $

(9)

式中:第一项表示联合概率密度的后验期望，第二项表示q分布的熵.根据式(3)~(6)的表达式，式(9)可表示为

$ \begin{gathered} L\left( q \right) = {\mathbb{E}_q}\left[ {\ln p\left( {\mathit{\boldsymbol{Y}}\left| {\left\{ {{\mathit{\boldsymbol{A}}^{\left( n \right)}}} \right\},{\tau ^{ - 1}}} \right.} \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;{\mathbb{E}_q}\left[ {\sum\limits_{n = 1}^N {\ln p\left( {{\mathit{\boldsymbol{A}}^{\left( n \right)}}\left| \lambda \right.} \right)} } \right] + {\mathbb{E}_q}\left[ {\ln p\left( \lambda \right)} \right] + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;{\mathbb{E}_q}\left[ {\ln p\left( \tau \right)} \right] - {\mathbb{E}_q}\left[ {\sum\limits_{n = 1}^N {\ln q\left( {{\mathit{\boldsymbol{A}}^{\left( n \right)}}} \right)} } \right] - \hfill \\ \;\;\;\;\;\;\;\;\;\;\;{\mathbb{E}_q}\left[ {\ln q\left( \lambda \right)} \right] - {\mathbb{E}_q}\left[ {\ln q\left( \tau \right)} \right]. \hfill \\ \end{gathered} $

(10)

将式(6)~(8)的更新关系式代入上式，可得出精确解，在此不再展开.

5) 模型推断的初始化

避免迭代过程中的跟踪停滞问题，选择一个初始值较为关键^[17].模型中$ a_{0}^{\tau }, b_{0}^{\tau }, {{c}_{0}}, {{d}_{0}}$设定为10^-6，使之产生非信息的先验.此时超参数的期望初始值为$\mathbb{E}\left[\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \right]=I, \mathbb{E}\left[\tau \right]=I $.对因子矩阵$\mathbb{E}\left[{\mathit{\boldsymbol{A}}{^{(n)}}}\right] $来说，可采用两种不同初始化方案.一种是对每个行向量$\{ {\rm{ }}\mathit{\boldsymbol{a}}_{{i_n}}^n\} $，从N(0, I)中随机选择; 另一种是设定为$\mathit{\boldsymbol{A}}{^{(n)}} = {\rm{ }}\mathit{\boldsymbol{U}}{^{(n)}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{\left( n \right)1/2}} $，其中 U⁽ⁿ⁾代表左奇异向量，Σ^(n)1/2代表奇异值的对角阵，它们从接收数据的模n矩阵的SVD分解中得到. V⁽ⁿ⁾设定为$ \mathbb{E}\left[{{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{{\rm{-1}}}}} \right]$.张量的秩R为信源节点的发射天线数.

整个算法推断过程见表 1.

3 仿真分析

在计算复杂度方面，由于本文算法与ALS及NLS算法均属于迭代类算法，在每次迭代计算复杂度和收敛速度方面可进行对比; 而文献[4~5, 9]属于非迭代类算法，与本文算法不具有可比性，值得强调的是，这些算法的复杂度要小于本文算法.在信道估计性能方面，本文算法可与基于监督序列的BALS算法，基于ALS和NLS半盲算法进行对比.

设定信道矩阵 H^(SR)及 H^(RD)是独立同分布的，其元服从复数高斯分布，分布的均值为零，方差分别为1/M_S，1/M_R.信道噪声为零均值，单位方差的加性高斯白噪声.信息源符号矩阵$\mathit{\boldsymbol{S}} = \sqrt {{E_{\rm{S}}}} {S_0} $从8PSK字母表随机产生，服从高斯分布，其中S₀为单位能量的符号矩阵，E_S为每个符号的平均能量. S 和 H^(RD)的第一行是已知的，这样满足了消除尺寸模糊的条件.选用的编码矩阵为截断DFT矩阵，保证了 C 是列满秩.中继增益 G 为随机生成器产生的范德蒙矩阵.这种设计避免了 H^(RD)和 H^(SR)的置换模糊.

3.1 计算复杂度

对算法每次迭代过程中运算复杂度进行分析比较.算法式(6)中因子矩阵的计算成本为$o({R^2}{M_{\rm{D}}}JP{N_{\rm{S}}}{\Sigma _n}{I_n} + M_{\rm{S}}^3{\Sigma _n}{I_n}) $，式(7)中λ的计算成本是$ o({M_{\rm{S}}}^2{\Sigma _n}{I_n})$，式(8)中τ的计算成本是$o({M_{\rm{S}}}^2{M_{\rm{D}}}JP{N_{\rm{S}}}) $.因此在本文算法总的计算复杂度是$o\left( {\left( {{M_{\rm{S}}}^3 + {M_{\rm{S}}}^2{M_{\rm{D}}}JP{N_{\rm{S}}}} \right)\left( {{M_{\rm{D}}} + P + {N_{\rm{S}}}} \right)} \right) $，与接收数据的维度大小呈线性关系，而与源天线数成多项式关系.算法NP-NLS与NP-ALS的计算复杂度见表 2.设定一定场景对三种算法的单次迭代运算复杂度进行对比，场景参数为：P = J = 4，N=8，计算结果如图 4所示.从图中可看出，本文算法计算复杂度明显低于NP-ALS，但高于NP-NLS，这是因为NLS采用了非线性搜索方法.值得一提的是，当M_S等于1和2时，计算复杂度仅为ALS的一半左右，此时计算复杂度的优势较为明显.

3.2 收敛速度

验证算法的收敛速度，并将其与NP-ALS及NP-NLS算法进行对比.仿真参数为：M_S=M_D=M_R=2，E_S=15 dB，N_S=8.因子矩阵$\{ {\rm{ }}{{\mathit{\boldsymbol{\tilde H}}}^{({\rm{RD}})}}, {\rm{ }}\mathit{\boldsymbol{\tilde H}}{^{({\rm{SR}})}}, {\rm{ }}\mathit{\boldsymbol{\tilde S}}{\rm{ }}\} $的初始值分别采用以下两种赋值方法：1)从高斯分布中随机取值(Randn); 2)对接收数据进行SVD分解后，对其进行赋值(SVD).引入平均重建误差(Reconstruction Error)，并将其与迭代次数建立联系.重建误差定义为^[7]

$ {\varepsilon _k} = \left\| {\mathit{\boldsymbol{x}} - {{\left( {\mathit{\boldsymbol{S}}_k^{\rm{T}} \otimes {\mathit{\boldsymbol{G}}^{\rm{T}}}} \right)}^{\rm{T}}} \odot \left( {\mathit{\boldsymbol{C}} \otimes \mathit{\boldsymbol{\hat H}}_k^{\left( {{\rm{RD}}} \right)}} \right)h_k^{\left( {{\rm{SR}}} \right)}} \right\|_2^2. $

式中 x 为接收张量的向量表示形式，$ \otimes $为Kronecker积.

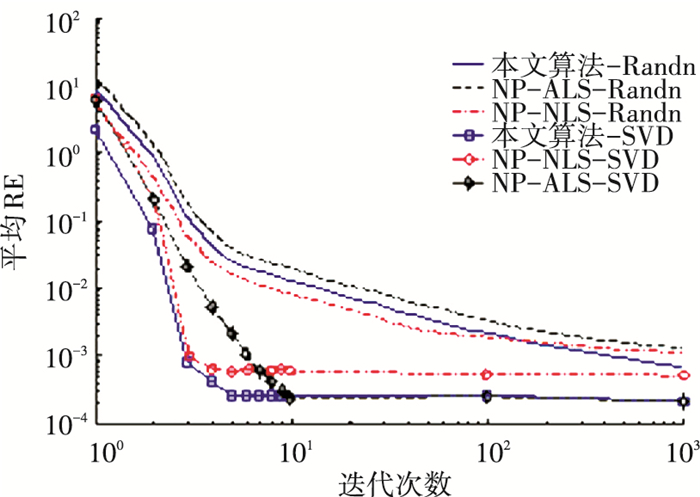
仿真结果如图 5所示.从图中可看出：整体上看，第二种赋值方法的收敛速度要明显快于第一种，这是因为DKRF首先对接收数据进行主成分分析，锁定了因子矩阵所在取值区域，然后再进行局部搜索.上述过程省去了全局搜索的迭代过程.两种赋值方法中，本文算法的收敛速度要快于NP-ALS，接近NP-NLS.但值得注意的是，虽然NP-NLS的收敛速度较快，但收敛时的平均RE要明显大于另二者，从另一角度来说，NP-ALS的信道估计精度要差于本文算法.

3.3 估计性能

对算法的估计性能进行分析，将其与基于监督序列的BALS算法，基于ALS和NLS半盲算法进行对比.具体方式是通过在CSI完全已知的场景下，利用提出的接收算法完成符号和信道估计，并对结果进行评估，评估的指标为误符号率(Symbol Error Rate，SER)性能和信道均方误差(Normalized Mean Square Error，NMSE). SER为多次Monte Carlo仿真的SER取平均，而信道的NMSE定义为

$ {\rm{NMSE}} = \frac{1}{K}\left( {\sum\limits_{k = 1}^K {\frac{{\left\| {{\mathit{\boldsymbol{H}}_k} - {{\mathit{\boldsymbol{\hat H}}}_k}} \right\|_{\rm{F}}^2}}{{\left\| {{\mathit{\boldsymbol{H}}_k}} \right\|_{\rm{F}}^2}}} } \right). $

式中:K为Monte Carlo运行次数，K=10 000，每次运行数据流NKM_S=10 000 NM_S. H_k为第k次运行所产生的模拟信道，$ {{\mathit{\boldsymbol{\hat H}}}_k}$为经过算法估计后的信道，其余仿真参数为：M_S=M_D=M_R=2，N_S = P = J = N = 2，ALS及NLS收敛误差为10^-3，a₀^τ，b₀^τ，c₀，d₀设定为10^-6，噪声方差为1.

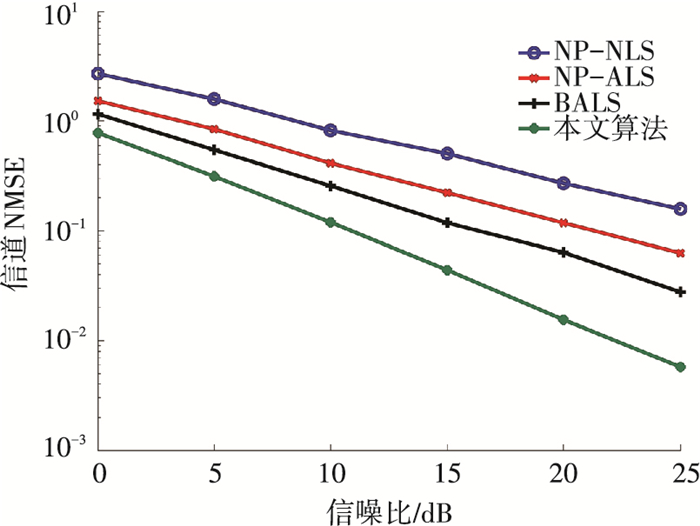
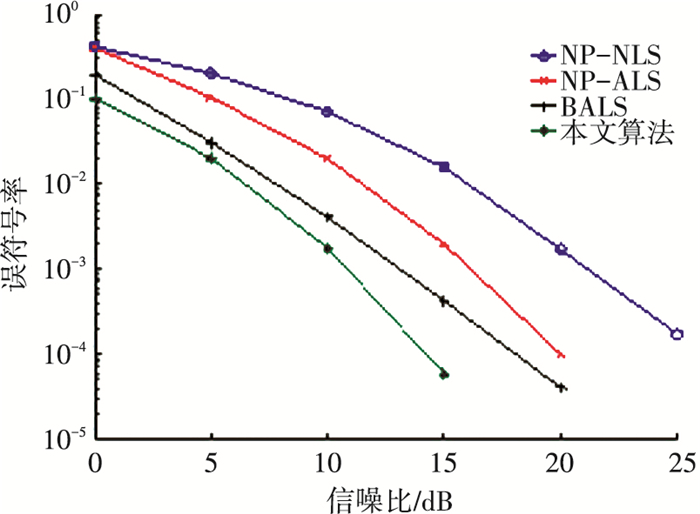
信道NMSE和SER分别见图 6、7.由于采用的噪声方差为1，图中的信噪比即为符号能量.从图中可以看出：信道NMSE方面，在相同信号能量情况下，算法引入了信道的先验信息，其信道估计性能优于BALS，NP-ALS及NP-NLS算法，由于非线性搜索易产生局部收敛，NP-NLS性能较差; 当符号能量增大时，NP-NLS的性能提升有限，而本文算法的估计性能要大幅优于其它三种算法.在SER方面，由于符号矩阵与信道矩阵同为接收数据的因子矩阵，本文算法的估计性能也优于其它三种方法，另一角度的解释是，仿真场景假设了符号矩阵也服从随机高斯分布，并将其引入因子矩阵的先验信息.从以上可以看出，本文算法的估计性能优于其它三种算法.尤其是在符号能量较大时，本文算法性能优势更为明显.

值得一提的是，该仿真中的信道特性为平稳瑞利衰落，在实际应用中，可根据实际信道特性对概率模型分布进行修正; 若没有真正的先验知识或要使估计更客观，可选择无信息的先验，比如Jeffrey先验等; 另外，该算法分析了基于Nested-PARAFAC张量分解的信道估计模型，在分析过程中，推导过程不失一般性，即该算法可推广至其它的张量分解模型，如Nested-Tucker张量分解中^[7].

4 结语

本文设计一种基于贝叶斯架构的信道估计方法.该算法基于Nested-PARAFAC张量模型，引入因子矩阵精度、噪声精度等隐性超参数，建立信道估计概率模型，在最大化模型证据意义上，采用变分贝叶斯推断逼近信道参数及符号矩阵的后验分布.该算法可通过隐性超参数将信道先验信息引入到概率模型中，并具有闭环解的后验近似及计算高效率的优势.仿真结果表明算法与现有监督序列的估计算法，基于ALS及NLS的算法相比，具有较高的估计性能.本文所提算法的推导过程具有一般性，可推广至基于其它张量分解的MIMO中继系统的半盲信道估计中.