2. 深部岩土力学与地下工程国家重点实验室(中国矿业大学), 江苏 徐州 221116;
3. 江苏省建筑工程质量检测中心有限公司, 南京 210008
2. State Key Laboratory for Geomechanics & Deep Underground Engineering(China University of Mining and Technology), Xuzhou 221116, Jiangsu, China;
3. Jiangsu Testing Center for Quality of Construction Engineering Co., Ltd., Nanjing 210008, China
大跨屋盖结构具有质量轻、柔度大、自振频率低和阻尼小等特点,属于风致敏感型结构,因而风荷载成为控制屋盖结构设计的主要荷载.当来流非垂直于迎风墙面到达屋盖迎风前缘处,边界层将发生流动分离且在屋盖表面两侧迎风前缘出现一对锥形涡结构.虽然屋盖迎风前缘分离流动区范围较小,但其形成的卷吸力却达到整个屋盖的最大值,此外在风压脉动作用下可能致使屋盖产生疲劳破坏,在两者的综合作用下最终导致屋盖被掀翻.
国内外学者对于锥形涡诱导下风压的时域和频域特性已开展了一系列的研究工作.Kawai[1]通过风洞试验研究了均匀流和湍流场中平屋盖表面平均和脉动风压分布,发现锥形涡作用下屋面风压呈现钟形分布规律,并通过测点风压定位了两种流场下锥形涡位置,指出湍流场下锥形涡涡轴的位置更偏向于迎风前缘,此外还比较了两种工况下屋面风压数值差异.Bank等[2-3]对平屋盖模型同时进行了流动显示和测压试验,结果表明屋面最大风吸力点位置一般位于锥形涡涡核之下.Wu等[4]指出锥形涡诱导下的风压脉动是由锥形涡涡轴的低频摇摆和高频旋转运动形成,此外,由于瞬时风向的不断变化,旋涡形状也在发生改变,因此屋面风压也随之发生脉动.陈学锐等[5]通过风洞测压试验研究了立方体屋盖结构锥形涡诱导下屋面风压分布特征,结果表明屋盖对角线两侧形成两个瓣状的强吸力区,吸力幅值随着与迎风角距离的增加而逐渐衰减.孙瑛等[6]对平屋盖锥形涡进行了探讨,给出了如何通过风洞试验数据识别其特征参数的方法,对锥形涡的涡心位置、作用范围以及运动模式等特征参数进行详细研究,并给出了定量结果.Kasperski等[7]研究了在最不利风向下低矮房屋迎风墙面、迎风屋面、下风屋面及背风墙面的风压谱,给出其各自的谱形状,但未给出具体的风压谱公式.
本次研究是以均匀流、格栅紊流和B类地貌3种不同来流为载体,利用刚性模型风洞测压试验研究了不同来流工况下平屋盖模型在典型风向下屋面的平均和脉动特性,分析不同来流工况、不同风向角下旋涡涡轴的运动特征,重点研究了锥形涡作用下涡轴方向各测点的风压脉动自功率谱和互功率谱特性,利用脉动风压频谱特性解释了旋涡运动与湍流尺度之间的演变关系.
1 大跨屋盖测压试验方案 1.1 试验模型设计风洞测压试验在湖南大学风工程试验研究中心大气边界层风洞HD-2高速试验段完成.如图 1所示,试验所用的屋盖模型均为刚性模型,采用有机玻璃制成.平屋盖底面为正方形,边长780 mm×780 mm,高度312 mm.参考点高度处风速控制在10 m/s,试验中每个测点采集6 600个数据.考虑到风洞试验段的截面尺寸,将屋盖模型的几何缩尺比设为1:200,阻塞率约为3%,模型相似比设计见表 1.

|
图 1 平屋盖试验模型 Figure 1 Model of the flat roof |
| 表 1 模型相似比 Table 1 Scaling laws for the model |
对于均匀流场,模型前方来流入口处未放置任何尖塔和矩形质量块,整个流场截面上各点的风速与来流风速基本一致,试验测得的顺风向、横风向和竖向湍流度分别为0.449%、0.277%和0.213%,可见均匀流场的湍流度非常小,可以忽略不计.
对于格栅紊流场,来流入口处放置由有4个水平和3个竖向板条正交组成的格栅网,水平和竖向板条宽度均为20 cm.文献[8]指出在格栅开口处形成射流,在距格栅一定范围内生成近似各向同性的紊流,本次试验测得的模型高度处顺风向、横风向和竖向湍流度分别为9.95%、8.47%和9.09%.
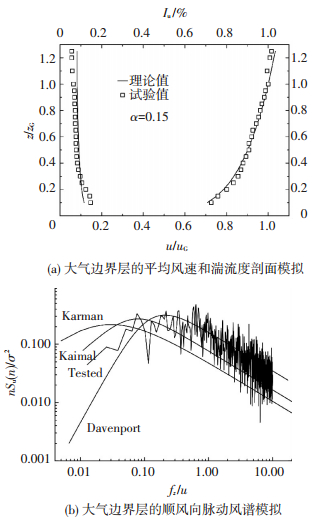
试验模拟B类地貌的平均风速剖面及湍流度剖面分布见图 2.
|
图 2 风洞中对B类风场的模拟 Figure 2 Wind tunnel simulation of the terrain B |
图 2(a)的平均风速剖面曲线理论值取自中国建筑结构荷载规范,湍流度剖面曲线理论值取自日本AIJ建筑规范.其中,ZG和UG分别为梯度风高度和梯度风高度处的风速,Iu为湍流度.图 2(b)给出了3种经典理论脉动风速谱和试验实测风速谱的对比.图中横坐标为折减频率,纵坐标为无量纲化的功率谱密度值,其中,n和z分别表示脉动风频率和屋盖的特征高度,u为特征高度处的平均风速,σ2为顺风向风速脉动值的方差.
本次风洞试验的测压信号采样频率为331 Hz,采样时长一般以保证对应于原型值不小于10 min为宜.根据表 1,该采样时间换算到原型为1 993 s,即33 min,大于荷载规范规定的10 min.综上所述,所测得的试验结果准确可信.
1.3 测压点布置及数据处理如图 3所示,屋盖表面共布置336个测点,规定向下压力为正,向上吸力为负.

|
图 3 风向和模型测点分布(mm) Figure 3 Definition of flow directions and tap locations (mm) |
测点的风压值采用风压系数来表示[9]:
| $ {C_{p,i}} = \frac{{{P_i} - {P_{静}}}}{{{P_{总}} - {P_{静}}}} $ |
式中:Pi为模型第i个测孔测得且修正后的表面风压值;P总和P静分别为参考点处的平均总压和平均静压.对数据进行处理得到平均风压系数Cp, mean和脉动风压系数Cp, rms.
2 试验结果分析 2.1 不同风场下屋面风压分布特征图 4给出了30°典型风向下3种来流工况屋面的平均和脉动风压系数分布.图中上三角区和下三角区界限是以迎风顶点处对角线划分的.

|
图 4 锥形涡作用下屋盖表面风压系数等值线(30°风向) Figure 4 Pressure coefficient contour on flat roof surface under the action of conical vortex (30° wind direction) |
由图 4可见:1)3种不同流场下,屋面的平均和脉动风压系数均呈现不对称的三角形分布,下三角区域的锥形涡尺寸和强度明显强于上三角区[10]; 2)屋面最大平均、脉动风压系数均出现在下三角区的迎风顶点附近,风压梯度大且变化剧烈.沿着锥形涡涡轴方向,随着与迎风顶点距离的增大,锥形涡的作用范围也在扩张,但风压系数在不断减小; 3)对比3种不同来流工况下的风压可以看出,均匀流和格栅紊流下的平均风压系数最大值达到了-4.5,而B类地貌只有-3.2,相反,格栅紊流场和B类地貌下的脉动风压系数是均匀流场的两倍左右.分析其原因是由于B类地貌下由于质量块的阻挡导致来流有一部分风能转化为湍动能,导致到达屋面后平均风压系数较小,而风压脉动得到加强;格栅紊流既没有任何阻挡又人为干预保持屋面高度处湍流度稳定在10%,因此其风压系数达到了均匀流和B类地貌两种工况的峰值.
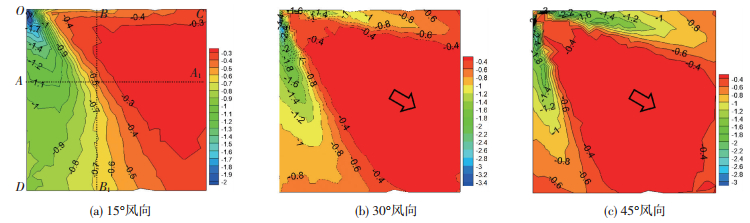
2.2 不同风向角下屋面风压分布特征图 5和图 6分别给出了B类地貌下屋盖表面平均、脉动风压分布的风洞试验结果随风向角(15°、30°、45°)的变化趋势,图中箭头代表风向.为了更加细致把握屋面流动结构特征,在屋面上选取分别与迎风边缘垂直的两个线段AA1和BB1,截面A-A1和截面B-B1分别与各自平行的迎风边缘距离0.4L(图 5(a)),两截面上的平均风压分布曲线如图 7所示(鉴于对比分析,图中也给出了0°风向下风压分布曲线).
|
图 5 不同风向角下平屋盖平均风压系数 Figure 5 Wind pressure coefficient on flat roofs with different wind directions |

|
图 6 不同风向角下平屋盖脉动风压系数 Figure 6 Wind fluctuation pressure coefficient on flat roofs with different wind directions |
|
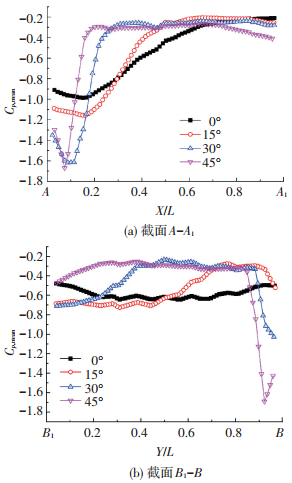
图 7 不同风向角下关键截面处平均风压系数 Figure 7 Average wind pressure coefficient at the critical cross section with different wind directions |
如图 7(a)所示,风向角θ为0°时,分离泡在0.18L位置处诱导出最大平均吸力-1.0,呈现出二维特征.随着θ增大至15°,沿着迎风前缘OD风向的轴向速度分量也随之增大,导致分离剪切层强度得到加强,具有一定的三维效应.由图 5(a)可见,屋面的下三角区风压呈现明显的多层级阶梯状分布,证明在下三角区形成了单侧锥形涡结构.θ=15°时截面A-A1压力分布曲线峰值吸力与θ=0°相比有所提高.此外,OC一侧由于气流量和卷吸速度的不足难以形成旋涡结构,导致其最大风吸力只有-0.5(图 7(b)).
随着θ继续增大至30°,沿着OD边缘的轴向分速度进一步加大,锥形涡的卷吸速度和强度也因此得到增强,从图 7(a)的平均风压曲线看,30°风向下的峰值风压陡然增大,最大风吸力逐渐向迎风边缘OD靠近以致高负压区范围减小.同时注意到,OC侧也开始出现多层级阶梯状风压分布,说明分离的剪切层卷吸强度已达到形成锥形涡的条件,OC边缘峰值吸力也由-0.4增至-1.0(图 7(b)).根据国外流动显示试验结果[11],在靠近来流一侧的下三角区域的锥形涡尺寸较大,而远离来流的上三角区域锥形涡尺寸较小.
当θ为45°时,对角线两侧的风压基本一致,呈现对称分布,说明两侧的锥形涡强度相当.对比图 5各子图可知,锥形涡的强度是在30°时达到最强,原因是斜风向下来流在迎风顶点O点速度可以分解为沿OD和OC两个方向的分速度,随着θ的逐渐增大,对下三角区锥形涡强度起增强作用的OD方向速度持续增大,而对锥形涡强度起削弱作用的OC风向分速度在持续减小.可以看出,下三角区域锥形涡是在两种此消彼长的相反机制作用下发展的,30°是两种速度机制对锥形涡共同作用达到最佳状态的风向角.
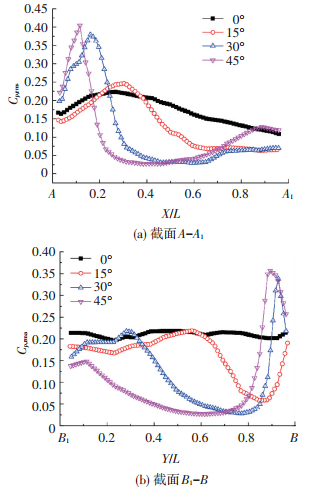
图 8给出了截面A-A1和截面B1-B上脉动风压曲线分布,可见风向角的增大导致脉动极值区域的缩小且逐渐向迎风边缘靠近.值得注意的是,斜风向下各曲线的脉动峰值点与迎风边缘的距离要大于平均峰值点与迎风边缘的距离,这是由锥形涡的再附点位置与涡核中心的位置决定.
|
图 8 不同风向角下关键截面处脉动风压系数 Figure 8 Fluctuation wind pressure coefficient at the critical cross section with different wind directions |
根据以往研究表明[12-13],锥形涡运动模式具有两个重要特征:围绕涡轴的圆周运动(涡轴是旋涡运动中心的连线)和旋涡再附作用的范围,最大平均风吸力一般位于各涡中心位置处,因此可以根据屋面风压分布的极值判断旋涡中心的位置.如图 9所示,当来流风向角为θ时,选取6个代表性截面,根据各截面内屋面最大风吸力值确定锥形涡涡心位置,定义涡轴与下三角区的迎风前缘平均夹角为α,再附线与下三角区的迎风前缘平均夹角为λ.

|
图 9 锥形涡结构关键特征点 Figure 9 Key features of conical vortex flow structures |
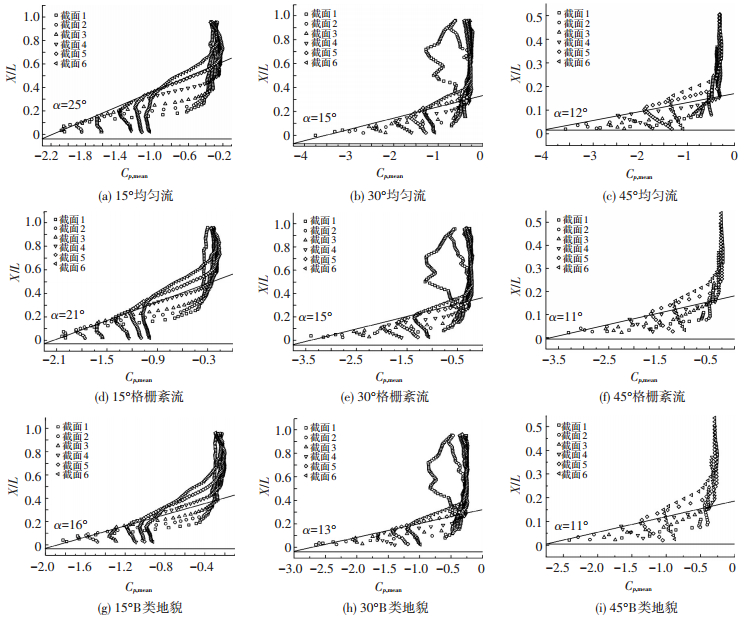
图 10给出了3种来流工况在风向角15°、30°和45°下的6个截面内风压分布曲线,X表示各截面测点与左侧边缘的垂直距离,L为屋面边长.由图可见,各个截面的平均风吸力值均是由迎风顶点处沿着迎风边缘先增大后逐渐减小的发展模式,这也是风压值在涡中心处达到极值的重要体现.15°风向下3种来流工况的涡轴与迎风边缘夹角α分别为25°、21°和16°,由此可见,当锥形涡尚未成熟时,随着湍流度的增大,涡轴是逐渐向迎风边缘靠拢.当风向角为30°和45°时,风吸力的峰值走向更加清晰,3种来流工况下α分别维持在15°、11°.此外,在同一来流工况下,随着风向角的增大,涡轴与迎风前缘的夹角在逐渐减小,这意味着锥形涡的影响范围也在缩小.
|
图 10 不同风向角和不同来流下锥形涡涡轴位置 Figure 10 The scroll axis position with different wind direction and different flow conditions |
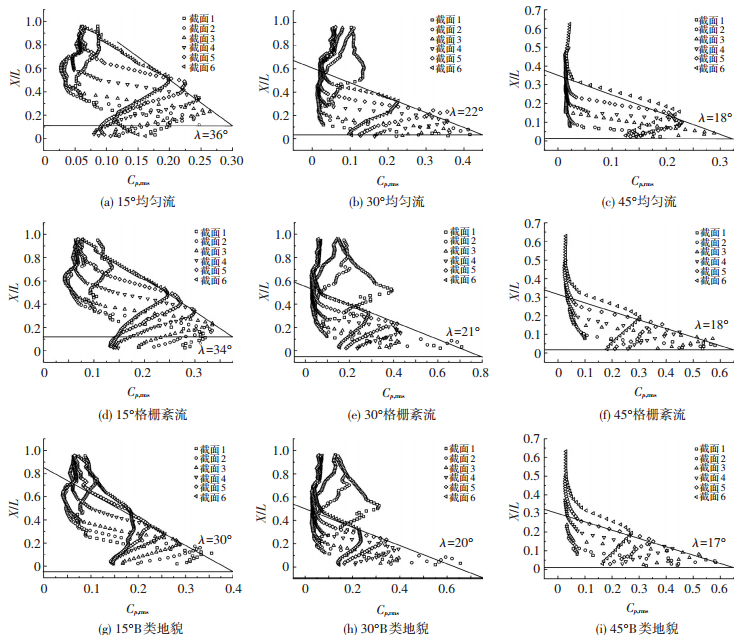
如图 11所示,通过各截面的最大脉动风压值确定锥形涡的再附作用范围.3种来流工况下15°风向锥形涡的再附作用范围与迎风前缘的夹角λ分别为36°、34°和30°,同涡轴与迎风边缘的夹角α具有相同的特征,随着湍流度增大,再附作用范围逐渐缩小;当锥形涡发展稳定后不同来流工况同一风向角的再附范围基本一致,在风向角为30°时旋涡的再附作用范围大于45°工况,但风吸力在30°风向达到极大.15°下锥形涡作用范围较大是由于此时旋涡同时具有分离泡和锥形涡特征.从30°开始,上三角区锥形涡的再附作用范围开始逐渐增大,对应的风吸力也在增大,从来流的能量守恒角度看,下三角区锥形涡作用范围和风吸力均在不断减小,因此锥形涡的再附作用范围与风吸力大小成正比关系.
|
图 11 不同风向角和不同来流下锥形涡再附作用范围 Figure 11 The attachment area with different wind direction and different flow conditions |
为了进一步考察锥形涡作用下测点在涡轴方向和横风向波动的频谱特征,基于均匀流、格栅紊流和B类地貌3种来流工况分析30°风向下涡轴方向测点列Col-3和横风向测点列Row-4在锥形涡诱导下的脉动风压功率谱(行和列的编号均取该行或该列的首个测点编号,各测点位置见图 12).由于30°风向平屋盖下三角区锥形涡诱导的风压最为强劲,此处仅研究屋盖下三角区涡轴测点的脉动风压谱.
|
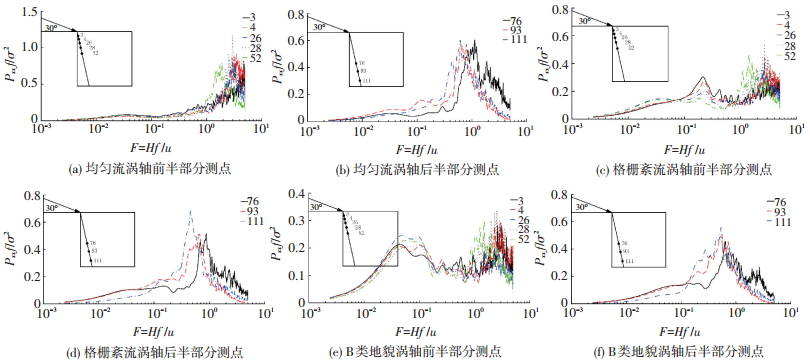
图 12 3种来流工况涡轴方向测点脉动风压谱 Figure 12 Three kinds of fluctuate wind pressure spectrum in the direction of vortex axis |
如图 12所示,由于锥形涡沿涡轴方向经历形成与发展的强吸力和旋涡脱落弱吸力两个阶段,因此将涡轴方向测点分为前半段和后半段两种情况进行探讨.由图 12(a)可看出,在均匀流场作用下,平屋盖涡轴方向测点脉动能量在低频段(F < 0.1)接近于零,分析其原因是均匀流场中湍流尺度成分单一且均匀,导致其脉动能量很小.相比之下,风压谱在高频段(F>1)表现特别突出,各测点的谱能量都接近于1,说明来流风能量大部分转化成锥形涡的高频旋转运动,风压表现为在迎风顶点处极值达到-4.8(表 2).沿涡轴方向往下游发展时,锥形涡能量在不断消耗,因此从图 12(b)可看出,屋盖后方测点的谱能量降低至0.6,且不断在往中频段(0.1 < F < 1)发展,屋面的平均、脉动风压系数均在不断减小.
| 表 2 平屋盖涡轴方向测点风压时程统计值 Table 2 Statistical value of wind pressure time history in vortex axis direction |
由图 12(c)、(e)可看出,格栅紊流和B类地貌下的测点风压谱能量在中低频段显著强于均匀流,但在高频段谱峰值有所降低,分析原因:湍流场中小尺度涡成分促使分离剪切层卷吸成锥形涡,大尺度涡成分则是加快锥形涡的旋转速率和维持涡轴左右摇摆的低频运动[14],锥形涡的这种运动形式造成了屋面的剧烈震荡.从风压表现上看,B类地貌由于旋涡涡轴的频繁运动导致平均风压最低,但风压脉动现象最为显著;而格栅紊流场是具有一定湍流度大小的均匀流场,其风压表现介于均匀流和B类地貌两者之间.
综上分析可看出,风压谱谱峰值与其对应的屋面风吸力存在一定关系.具体叙述如下:对于涡轴方向迎风点附近测点(锥形涡形成发展阶段),在高频段(F>1)范围内,相应频率对应的谱能量峰值越大,则屋盖在锥形涡诱导下的平均风吸力越大;在低频段(F < 0.1)范围内,相应频率对应的谱能量峰值越大,则屋盖在锥形涡诱导下的脉动风吸力越大,同时高频段对应的能量谱峰值显著强于低频段.对于涡轴方向后方测点(锥形涡脱落阶段),由于脱落后形成大量微尺度涡,中高频能量大,但其平均和脉动风压均表现较弱.
图 13给出了3种来流工况下涡轴方向各测点间的脉动风压互谱.在均匀流作用下,涡轴方向各测点间的脉动风压互谱曲线整体看比较平稳且相关性较弱,测点3与测点26的谱峰值只有0.02,测点3与其他各点的功率谱均是接近于零的平直线,说明虽然均匀流作用下在迎风顶点处表现最强吸力,但屋面各测点间同时达到风压极值的概率小;而对于两类紊流场,迎风顶点附近测点互谱曲线均呈现指数衰减模式.从图 13(b)、(c)可知,测点3、26的互谱曲线高频段的相关性为负值,这是由于锥形涡的二次再附形成次级旋涡所致,主涡和次级涡脉动方向相反,两种旋涡的共同工作引起迎风顶点附近区域的强劲风压.

|
图 13 3种来流工况涡轴方向各测点间的脉动风压互谱 Figure 13 Pressure fluctuation power spectrum between each point with three flow conditions |
图 14给出了3种来流工况下横风向Row-4各测点间脉动风压谱.由图 14(a)、(c)、(e)可知,横风向锥形涡作用范围内测点的风压谱在3种来流工况的频谱特征同图 12涡轴方向前半测点相同,均匀流下为高频的锥形涡旋转运动,风吸力最强,随着来流湍流度的增大,低频风压脉动开始占优.对于未受到锥形涡影响的测点(图 14(b)、(d)、(f)),均匀流下的测点频谱能量分布在中高频段,低频能量依然微弱.从风压上看,旋涡内测点平均风压约是旋涡外测点的6倍之多(表 3).值得一提的是,对于旋涡内测点,湍流度增大使中低频能量显著增大;而对于旋涡外测点,湍流度增大并未促使低频段能量有较大上升.

|
图 14 3种来流工况横风向测点脉动风压谱 Figure 14 Pressure power spectrum of the cross wind fluctuation with three flow conditions |
| 表 3 横风向测点风压时程统计值 Table 3 Wind pressure time-history statistical values of cross wind direction |
1) 3种不同流场下,屋面的平均和脉动风压均呈现不对称的三角形分布,15°风向只在下三角区形成单侧锥形涡,随着风向角增大,迎风前缘两侧出现一对锥形涡结构.屋面最大平均和脉动值均出现在下三角区的迎风顶点附近,格栅紊流下屋面平均和脉动风压达到3种来流工况中最强.
2) 当锥形涡尚未成熟时(15°风向),随着湍流度的增大,涡轴是逐渐向迎风边缘靠拢,再附作用范围逐渐缩小;当锥形涡发展稳定后(30°和45°风向),不同来流工况下涡轴位置基本保持不变.对于同一来流工况下,随着风向角的逐渐增大,涡轴与迎风前缘的夹角和再附作用范围均在逐渐减小.
3) 涡轴方向迎风点附近测点风压谱谱峰值与其对应的屋面风吸力成正比例关系:在高频范围内,测点风压谱相应频率对应的谱能量峰值越大,屋盖平均风吸力也越大;在低频范围内,相应频率对应的谱能量峰值越大,其脉动风吸力也越大.均匀流下涡轴方向各测点间的相关性较弱,紊流下测点间的互谱曲线为指数衰减模式.
| [1] |
KAWAI H. Structure of conical vortices related with suction fluctuation on a flat roof in oblique smooth and turbulent flows[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1997, 69(97): 579-588. |
| [2] |
BANK S D, MERONEY R N, SARKAR P P. Flow visualization of conical vortices on flat roofs with simultaneous surface pressure measurement[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2000, 84(1): 65-85. |
| [3] |
BANK S D, MERONEY R N. A model of roof-top surface pressures produced by conical vortices: Evaluation and implications[J]. Wind & Structures An International Journal, 2001, 4(4): 279-298. |
| [4] |
WU F, SARKAR P P, MEHTA K C. Influence of incident wind turbulence on pressure fluctuations near flat-roof corners[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2001, 89(5): 403-420. |
| [5] |
陈学锐, 顾志福, 李燕. 锥形涡诱导下建筑物顶面风荷载[J]. 力学学报, 2007, 39(5): 655-660. CHEN Xuerui, GU Zhifu, LI Yan. Conical vortex induced wind loading on the roof of a building[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(5): 655-660. |
| [6] |
孙瑛, 武岳, 林志兴, 等. 大跨屋盖结构风压脉动的非高斯特性[J]. 土木工程学报, 2007, 40(4): 1-5. SUN Ying, WU Yue, LIN Zhixing, et al. Non-Gaussian features of fluctuating wind pressures on long span roofs[J]. China Civil Engineering Journal, 2007, 40(4): 1-5. |
| [7] |
KASPERSKI M, KOSS H, SAHLMEN J. Wind action on low-rise buildings[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1996, 64(2): 101-125. |
| [8] |
闫静, 唐洪武, 程年生. 振动格栅紊流及其应用综述[J]. 水利学报, 2005, 26(12): 153-159. YAN Jing, TANG Hongwu, CHENG Niansheng. Survey of turbulence in vibration grille and its application[J]. Journal of Hydraulic Engineering, 2005, 26(12): 153-159. |
| [9] |
孙晓颖, 武岳, 沈世钊. 大跨屋盖风压分布的数值模拟及拟合方法研究[J]. 哈尔滨工业大学学报, 2006, 38(4): 553-557. SUN Xiaoying, WU Yue, SHEN Shizhao. Numerical simulation of wind pressure distribution on long span roofs and curve fitting method[J]. Journal of Harbin Institute of Technology, 2006, 38(4): 553-557. |
| [10] |
WU F, SARKAR P P, MEHTA K C. Understanding the conical-vortex flow on roofs[J]. Wind engineering into the 21st century, 1999, 3(10): 1867-1874. |
| [11] |
MIN C H, YANG L X, CHENG-YING Q I, et al. PIV measurement of flow field in a rectangular channel with longitudinal vortex generators[J]. Journal of Hebei University of Technology, 2011, 15(3): 15-26. |
| [12] |
PINDADO S, MESEGUER J, FRANCHINI S. Influence of an upstream building on the wind-induced mean suction on the flat roof of a low-rise building[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2011, 99(8): 889-893. |
| [13] |
LIN J X, SURRY D, TIELEMAN H W. The distribution of pressure near roof corners of flat roof low buildings[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1995, 56(2): 235-265. |
| [14] |
TRYGGESON H, LYBERG M D. Stationary vortices attached to flat roofs[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2010, 98(1): 47-54. |
 2018, Vol. 50
2018, Vol. 50


