冷却塔作为一种空间高耸薄壳混凝土结构,其在风荷载作用下的安全性历来受到工程界的高度重视[1-2].已有研究主要采用风洞试验、数值模拟和有限元方法对冷却塔风荷载效应进行系统分析,涉及内外风荷载分布特性[3]、干扰效应[4]、风荷载作用下受力性能和稳定性[5]等,而现有针对冷却塔结构的现场实测研究主要集中在塔筒表面的风荷载分布特性[6-7].
文献[8]基于冷却塔内外表面测压风洞试验,在冷却塔表面多点脉动风荷载相关性分析的基础上,获得了冷却塔表面压力极值分布曲线; 文献[9]采用时程方法进行了结构动力响应计算,依据Davenport理论或由经验指定峰值因子,或者以时程最值为极值分别计算响应极值; 文献[10]基于高斯假定,对比分析了考虑不同导风装置下冷却塔峰值因子和极值风压分布的差异.
文献[11-12]前期在分析冷却塔表面风荷载随机特性时发现,壳体表面分离点和负压极值区域存在明显的非高斯特性,并提出了划分高斯及非高斯分布的定量标准; 文献[13]对某167 m高冷却塔进行了动态风压现场实测,给出了迎风面、侧面和背风面3个区域的概率密度函数,并对其高斯和非高斯特性进行了判别.近年来中国冷却塔建设日益朝着高大化发展,目前中国宁夏地区已建成220 m世界最高的超大型冷却塔,此类超大型冷却塔风致动态响应会呈现一定非高斯和非平稳特性,现有的基于高斯假定的极值估算方法[14]已不能完全适用,急需开展此类大型冷却塔结构动态响应的现场实测和极值分布研究.
为研究该问题,以中国西北地区某179 m大型冷却塔为对象,采用现场实测方法获取环境激励下塔筒典型部位的加速度振动信号,首先结合RDT(随机减量法)和NExT(自然激励技术)对信号进行预处理,再采用ARMA、ITD和STD三种模态识别方法获取冷却塔前10阶自振频率和阻尼比,并与有限元动力特性结果进行对比,再借鉴振型组合思路提出结构等效综合阻尼比.采用峰值因子和Sadek-Simiu两种极值估算方法计算加速度响应极值,并给出响应极值单一取值.最后基于完全瞬态时域法进行了实测阻尼比2%和规范阻尼比5%下的风振响应分析,对比两种阻尼比下平均、脉动和极值响应,并将有限元结果与实测响应极值进行对比和误差分析.
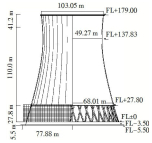
1 现场实测及结果分析 1.1 工程概况测试塔塔高179 m,喉部标高137.8 m,进风口标高27.8 m,塔顶直径103.2 m,喉部直径98.6 m,零米直径153.2 m.塔筒采用48对X型支柱支撑并与环板基础连接,X型支柱采用矩形截面,环板基础为现浇钢筋混凝土结构,宽为9 m,高为2 m.冷却塔所处地貌类别为B类,10 m高50 a一遇10 min平均最大风速为23.7 m/s.图 1给出了测试冷却塔及周边布置平面图, 表 1给出了测试塔主要尺寸参数列表.

|
图 1 测试冷却塔及周边布置平面示意 Figure 1 Cooling tower and the surroundings |
| 表 1 测试塔主要尺寸参数列表 Table 1 Main parameters of measured cooling towers |
测试仪器主要包括加速度传感器、动态信号测试分析系统、信号传输导线、电脑.其中传感器选择美国PCB压电式低频加速度传感器,灵敏度范围为900~1 100mV/g,频响范围可达0.025~800 Hz,满足采集冷却塔低频多向振动信号的试验要求.信号采集仪为DH5927动态信号测试分析系统,可实现实时控制、采集、存储和分析.该系统配备了完整的硬件和软件环境,具有极强的抗干扰能力,通过以太网通道扩展,实现多通道并行同步采样,并且具有信号长时间实时高速记录功能.
为精确识别测试塔主要低阶模态参数,沿塔筒外表面子午向和环向布设相应测点,具体布置如下:
1) 沿塔筒子午向高度共布设4个测点层,对应高度分别为145、110、70和30 m;
2) 测点层1和3沿环向均匀布置8个测点.
测点编号定义为A-B,其中A为子午向测点层号,B为环向测点编号.图 2给出了现场测试冷却塔测点布置示意图,图 3给出了冷却塔现场测试传感器安装示意图.

|
图 2 现场实测冷却塔测点布置示意 Figure 2 Arrangement of measuring points in the measured cooling tower |

|
图 3 冷却塔测试现场传感器安装示意 Figure 3 The diagram of sensors installation for field measurements |
采用上述实测系统进行环境激励下冷却塔风致响应现场实测,信号采集系统的采样频率设置为5 Hz,并对冷却塔塔筒典型部位的加速度响应振动信号进行连续观测.
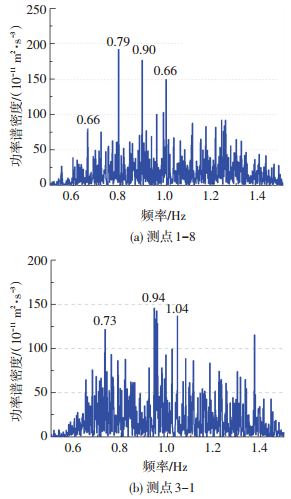
图 4给出了测试塔典型测点实测加速度响应功率谱密度曲线.由图可知,冷却塔多模态参与了振动,其中个别典型模态集中了较高的能量.现场实测所获得的振动加速度功率谱密度曲线出现了多处毛刺,峰值包含了结构自身的频率信息.为进一步准确获取结构模态参数,仍需结合多种方法进行模态识别.
|
图 4 典型测点实测加速度功率谱密度曲线 Figure 4 Power spectral density of acceleration responses of typical measuring points |
基于大型通用有限元分析软件ANSYS建立冷却塔结构有限元模型,塔筒离散为空间壳单元,环基及与环基连接的48对X型柱均离散为空间梁单元模拟,X型柱和下环梁处采用节点多自由度耦合约束,每个环基下部采用combin14单元模拟弹性地基,各方向弹簧刚度按照地基弹簧系数70 000 kN/m3取值,弹簧单元一端与环基刚性连接,另一端固结约束.
环境激励不同模态识别方法均可能存在丢失模态或虚假模态的情况[15],考虑到冷却塔具有自振频率分布密集的特点,为确保不丢失模态以及模态参数识别的正确性,本文主要采用两阶段时域识别方法,首先采用RDT[16]和NExT[17]从实测响应中提取结构的自由响应曲线或互相关函数,再结合ITD[18]、STD[19]和ARMA法[20]进行模态参数识别.
采用Block Lanczos方法求解冷却塔自振频率,图 5给出了实测与有限元分析冷却塔前10阶自振频率和阻尼比对比曲线.分析可知,实测与有限元方法拾取的冷却塔自振频率较为接近,基频最大相差6%,前10阶自振频率最大误差9%;不同识别方法得到的阻尼比结果离散性较大,多种方法在一定程度上填补了模态缺失,实测冷却塔前10阶阻尼比均在3.5%以下,小于规范值5%[21];前10阶阻尼比随振型的分布规律差异明显,采用RDT结合ITD和ARMA方法识别的结果与已有实测数据[22]分布规律较为一致.

|
图 5 实测与有限元前10阶自振频率和阻尼比对比曲线 Figure 5 First 10 order frequencies and damping ratios under measurement and finite element |
针对阻尼比识别结果具有离散性较大的特点,同时为便于设计取值,借鉴振型组合[23]的思路,采用前10阶模态的质量参与系数所占的百分比作为对应模态阻尼比的附加权重值,进而加权得到测试塔的整体结构等效综合阻尼比.
| $ {\xi _{{\rm{eq}}}} = \sum\limits_{i = 1}^{10} {{\eta _i}{\xi _i}} . $ | (1) |
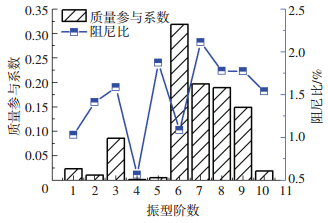
式中:ξeq为等效综合阻尼比,单位为%;ηi为第i阶模态的质量参与系数所占的百分比;ξi为第i阶模态阻尼比,单位为%.图 6给出了测试塔前10阶质量参与系数和阻尼比分布曲线.综合考虑不同方法识别结果的离散性,计算得到冷却塔等效综合阻尼比为2%.
|
图 6 冷却塔前10阶质量参与系数及阻尼比分布曲线 Figure 6 First 10 order proportion coefficients and damping ratios distribution curve of measured cooling tower |
冷却塔加速度响应极值计算公式为
| $ {a_{i,{\rm{peak}}}} = {a_{i,{\rm{mean}}}} + {\rm{sign}}\left( {{a_{i,{\rm{mean}}}}} \right) \cdot g \cdot {\sigma _i}. $ | (2) |
式中:ai, peak为加速度响应极值,ai, mean为加速度响应均值,σi为加速度响应均方差,g为峰值因子.
1) 峰值因子法
Davenport[24]假设脉动风压服从高斯分布,并基于高斯过程的零值穿越理论给出峰值因子.峰值因子表达式为
| $ g = \sqrt {2{\rm{ln}}\left( {\nu T} \right)} + \frac{\gamma }{{\sqrt {2{\rm{ln}}\left( {\nu T} \right)} }}. $ | (3) |
式中:γ为欧拉常数,取值为0.577 2;T为时程的时距;ν为单位时间内高斯时程的越零率.
2) Sadek-Simiu法
Sadek等[25]在零值穿越理论的基础上提出了非高斯过程的极值计算方法.在时距T内,时程y(t)的极值ypk, T的概率分布函数为
| $ {F_{{y_{pk,T}}}}\left( {{y_{pk,T}}} \right) = {\rm{exp}}\left[ { - {v_{0,y}}T{\rm{exp}}\left( { - y_{pk,T}^2/2} \right)} \right]. $ | (4) |
根据上式可得到指定概率Fiypk, T下的极值:
| $ y_{pk,T}^{{\rm{max}},i} = \sqrt {2{\rm{ln}}\frac{{ - {v_{0,y}}T}}{{{\rm{ln}}y_{pk,T}^i}}} , $ | (5) |
| $ y_{pk,T}^{{\rm{min}},i} = - \sqrt {2{\rm{ln}}\frac{{ - {v_{0,y}}T}}{{{\rm{ln}}y_{pk,T}^i}}} , $ | (6) |
式中v0, y为高斯过程y(t)的零值穿越率.
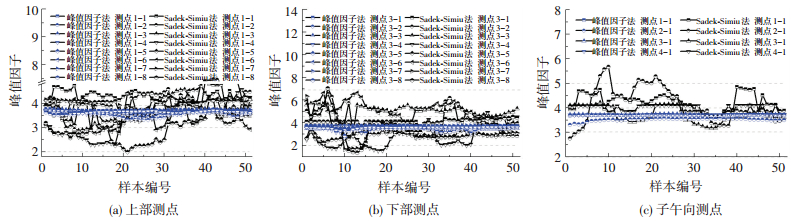
2.2 峰值因子取值图 7给出了不同极值估算方法冷却塔加速度响应峰值因子随样本变化曲线.图 8给出了不同极值估算方法冷却塔加速度响应峰值因子特征值.对比可知,采用Sadek-Simiu法计算的峰值因子对样本的敏感性较大,具体表现为随着样本的改变程度峰值因子波动显著.其中,采用峰值因子法获取的峰值因子数值在2.70~3.76,均值较为接近且数值最大相差0.23,不同样本的脉动程度较小;Sadek-Simiu法计算结果分布在1.38~7.47,均值在2.82~5.01,且不同样本计算的峰值因子脉动值最小为0.167,接近峰值因子法最大脉动值0.19.局部测点的峰值因子随样本变化产生明显的突变和跳跃现象,塔筒上部以测点1-2尤为显著,塔筒下部以测点3-7和3-8较为明显,子午向以测点4-1较为平稳,测点2-1峰值因子变化较大.
|
图 7 不同极值估算方法加速度峰值因子随样本变化曲线 Figure 7 Peak factors change with the sample of acceleration responses by different extremum estimation methods |

|
图 8 不同极值估算方法加速度峰值因子特征值 Figure 8 Feature values of peak factors change of acceleration responses by different extremum estimation methods |
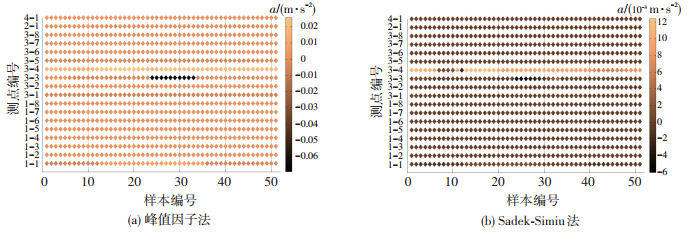
图 9给出了两种极值估算方法获得的结果随样本变化二维分布图,其中图 9(a)给出了加速度响应极值,图 9(b)给出了峰值因子法与Sadek-Simiu法的加速度响应极值差.由图可知,加速度极值响应随样本变化呈现出连续的变化趋势,仅局部时间点处受到大脉冲信号影响产生大突变现象;两种极值估算方法获得的加速度响应极值较为接近,仅局部测点和样本的极值分布差异显著.表 2给出了不同极值估算方法计算得到的实测加速度响应极值列表.可以看出两种极值估算方法计算得到的加速度极值响应接近,二者数值最大相差32.02%.
|
图 9 不同极值估算方法冷却塔加速度响应极值二维分布图 Figure 9 Extremums of acceleration responses for cooling tower by different extremum estimation methods |
| 表 2 不同极值估算方法冷却塔实测加速度响应极值 Table 2 Extremum acceleration responses of cooling tower by different extremum estimation methods |
采用完全瞬态法求解冷却塔瞬态动力学平衡方程,其核心是使用隐式方法Newmark和HHT来直接求解瞬态问题.在一个时间间隔内:
| $ \mathit{\boldsymbol{M\ddot u}} + \mathit{\boldsymbol{C\dot u}} + \mathit{\boldsymbol{Ku}} = {\mathit{\boldsymbol{F}}^a}, $ | (7) |
| $ {{\mathit{\boldsymbol{\dot u}}}_{n + 1}} = \left[ {{{\mathit{\boldsymbol{\dot u}}}_n} + \left( {1 - \delta } \right){{\mathit{\boldsymbol{\dot u}}}_n} + \delta {{\mathit{\boldsymbol{\ddot u}}}_{n + 1}}} \right]\Delta t, $ | (8) |
| $ {\mathit{\boldsymbol{u}}_{n + 1}} = {\mathit{\boldsymbol{u}}_n} + {{\mathit{\boldsymbol{\dot u}}}_n}\Delta t + \left[ {\left( {\frac{1}{2} - \alpha } \right){{\mathit{\boldsymbol{\ddot u}}}_n} + \alpha {{\mathit{\boldsymbol{\ddot u}}}_{n + 1}}} \right]\Delta {t^2}. $ | (9) |
式中α和δ为Newmark积分参数.仅采用Newmark方法计算有限元离散空间域无法满足算法要求,而结合HHT法可以弥补该弊端.
采用风洞试验获取的表面风压系数时程作为测试冷却塔的风荷载输入参数[26],选取实测等效综合阻尼比2%和规范[21]阻尼比5%分别作为阻尼比输入值,基本风速为实测平均风速6.78 m/s,计算时间积分步长为0.323 s,时间步数为2 048步,采用完全瞬态分析方法进行时域求解.
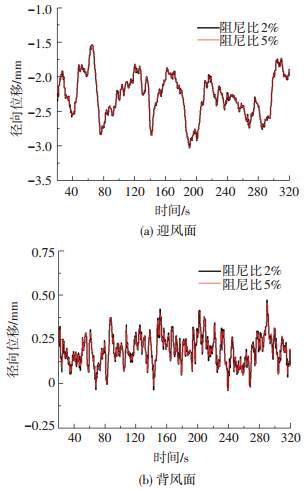
3.2 塔筒风致响应分布特性图 10给出了不同阻尼比塔筒喉部典型测点径向位移时程曲线.由图可知,响应时程均围绕均值上下一定范围波动,阻尼比的改变使得脉动程度产生变化.
|
图 10 不同阻尼比塔筒喉部典型测点径向位移时程曲线 Figure 10 Time histories of radial displacements of the typical measurement point at the throat under different damping ratios |
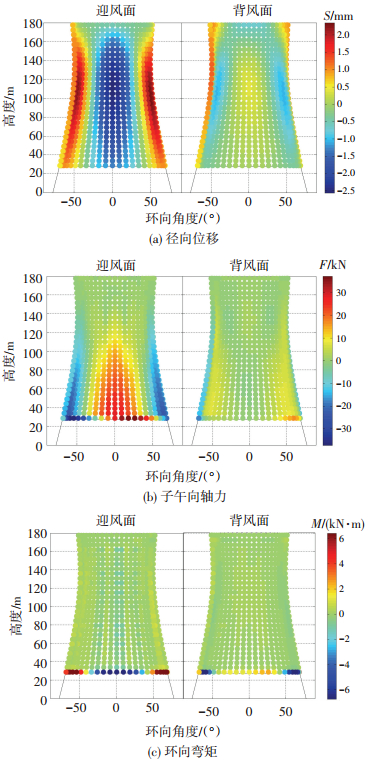
图 11给出了冷却塔塔筒平均响应分布图.由图 11可知:1)径向位移沿环向基本呈对称分布,沿环向呈现3个峰值,分别对应0°迎风面和±70°负压极值区域,背风区平均响应较小;2)径向位移分布具有明显的“三维效应”,刚性环的约束作用下呈现出中段大两端小的分布特征,最大位移出现在喉部位置;3)塔筒喉部以下位置子午向轴力较大,环向弯矩分布较均匀,塔筒下环梁与支柱连接区域产生局部应力集中现象.
|
图 11 冷却塔塔筒平均响应分布云图 Figure 11 Average responses of cooling tower cylinder |
图 12给出了不同阻尼比下塔筒脉动响应分布图.对比可知,阻尼比显著影响了脉动响应的分布,且塔筒不同位置脉动响应的变化程度不一致.阻尼比2%工况下塔筒径向位移较阻尼比5%下增加0.04%~2.76%,其中增量最值区主要集中在环向150~200°,且以塔筒中下部的增加较为显著.阻尼比2%下塔筒子午向轴力较5%阻尼比下增量最大为2.72%,72.3%数据的增量分布在0.2%~2%;阻尼比2%工况下环向弯矩增量分布在0.10%~5.49%,其中78.5%的数据增量集中在0.5%~3%.
|
图 12 不同阻尼比冷却塔塔筒脉动响应分布云图 Figure 12 Pulsation response of different damping ratios cooling tower cylinder |
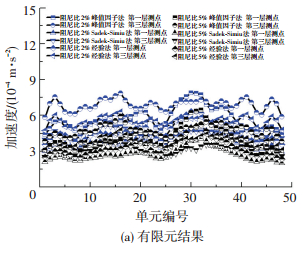
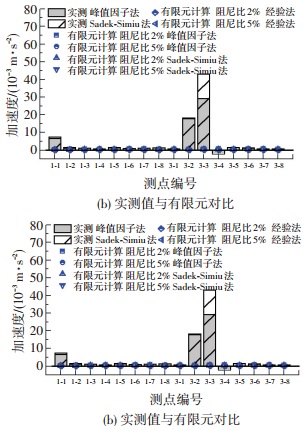
有限元风致响应极值计算中分别采用峰值因子法、Sadek-Simiu法和经验值2.5[27],图 13给出了实测与有限元计算的加速度响应极值对比示意图.由图 13可知,3种极值估算方法的有限元风致响应极值大小为:Sadek-Simiu法<经验取值<峰值因子法,阻尼比2%下第一层和第三层测点高度处加速度响应极值较阻尼比5%下增加最大分别为60.56%和66.79%.测点1-1、3-2、3-3和3-4的实测与有限元结果相差较大,测点1-4、1-6、3-1、3-7和3-8的加速度极值较为一致.其中测点3-7采用峰值因子法计算的实测极值与阻尼比2%下峰值因子法有限元极值结果仅相差2.29%.
|
图 13 实测与有限元计算加速度响应极值对比示意 Figure 13 Comparison of extreme value of the acceleration responses between measured and finite element |
1) 环境激励下冷却塔现场测试采用了合理的技术路线和先进仪器,获得的振动加速度曲线真实可靠,对类似的工程结构具有一定的参考价值,实测时冷却塔结构混凝土仍处于弹性变形阶段,分析所得的低阶频率和阻尼比均为冷却塔弹性变形阶段时的结果.
2) 实测与有限元分析两种方法获得的冷却塔自振频率较为接近,前10阶自振频率最大相差9%;实测冷却塔前10阶阻尼比均小于3.5%,小于规范值5%.本文所建立的塔筒-支柱-环基一体化冷却塔仿真模型具有可靠性,且为后续的风振瞬态分析提供有效支撑.
3) Sadek-Simiu法对样本的敏感性较峰值因子法明显,峰值因子法计算得到的峰值因子数值在3.49~3.72,Sadek-Simiu法得到的峰值因子在2.82~5.01;加速度响应均值、方差和极值均同步表现出显著的时变特性,两种极值估算方法获得的实测加速度响应极值最大相差32.02%.
4) 两种阻尼比下风振完全瞬态分析结果表明,阻尼比取值影响脉动响应,局部测点的有限元风致响应极值估算结果与实测极值较为一致.
| [1] |
VILADKAR M N, KARISIDDAPPA, BHARGAVA P, et al. Static soil-structure interaction response of hyperbolic cooling towers to symmetrical wind loads[J]. Engineering Structures, 2006, 28(9): 1236-1251. DOI:10.1016/j.engstruct.2005.11.010 |
| [2] |
ORLANDO M. Wind-induced interference effects on two adjacent cooling towers[J]. Engineering Structures, 2001, 23(8): 979-992. DOI:10.1016/S0141-0296(00)00110-3 |
| [3] |
沈国辉, 张陈胜, 孙炳楠, 等. 大型双曲冷却塔内表面风荷载的数值模拟[J]. 哈尔滨工业大学学报, 2011, 43(4): 104-108. SHEN Guohui, ZHANG Chensheng, SUN Bingnan, et al. Numerical simulation of wind load on inner surface of large hyperbolic cooling tower[J]. Journal of Harbin institute of technology, 2011, 43(4): 104-108. DOI:10.11918/j.issn.0367-6234.2011.04.021 |
| [4] |
张军锋, 葛耀君, 赵林. 群塔布置对冷却塔整体风荷载和风致响应的不同干扰效应[J]. 工程力学, 2016, 33(8): 15-23. ZHANG Junfeng, GE Yaojun, ZHAO Lin. Interference effects on global wind loads and wind included responses for group hyperboloidal cooling towers[J]. Engineering Mechanics, 2016, 33(8): 15-23. |
| [5] |
柯世堂, 赵林, 葛耀君. 超大型冷却塔结构风振与地震作用影响比较[J]. 哈尔滨工业大学学报, 2010, 42(10): 1635-1641. KE Shitang, ZHAO Lin, GE Yaojun. Comparison of super-large cooling towers under earthquake excitation and wind load[J]. Journal of Harbin Institute of Technology, 2010, 42(10): 1635-1641. DOI:10.11918/j.issn.0367-6234.2010.10.025 |
| [6] |
SUN T F, ZHOU L M. Wind pressure distribution around a ribless hyperbolic cooling tower[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1983, 14(1): 181-192. |
| [7] |
赵林, 刘晓鹏, 高玲, 等. 大型冷却塔表面脉动风压原型实测与分布准则[J]. 土木工程学报, 2017, 50(1): 1-11. ZHAO Lin, LIU Xiaopeng, GAO Ling, et al. Full-scale measurement and distribution rules of surface fluctuating wind pressure of a large cooling tower[J]. China Civil Engineering Journal, 2017, 50(1): 1-11. |
| [8] |
赵林, 李鹏飞, 葛耀君. 等效静风荷载下超大型冷却塔受力性能分析[J]. 工程力学, 2008, 25(7): 79-86. ZHAO Lin, LI Pengfei, GE Yaojun. Numerical investigation on performance of super lage cooling towers under equivalent static wind load[J]. Engineering Mechanics, 2008, 25(7): 79-86. |
| [9] |
张军锋, 葛耀君, 赵林. 冷却塔风振响应时程计算和风振系数分析[J]. 振动与冲击, 2017, 36(3): 163-171. ZHANG Junfeng, GE Yaojun, ZHAO Lin. Wind induced responses of a hyperboloidal cooling tower in time-domain and gust effect factor analysis[J]. Journal of vibration and shock, 2017, 36(3): 163-171. |
| [10] |
柯世堂, 朱鹏. 不同导风装置对超大型冷却塔风压特性影响研究[J]. 振动与冲击, 2016, 35(22): 136-141. KE Shitang, ZHU Peng. Impact of different air-deflector on the wind pressure on super-large cooling towers[J]. Journal of vibration and shock, 2016, 35(22): 136-141. |
| [11] |
柯世堂, 葛耀君, 赵林. 大型双曲冷却塔表面脉动风压随机特性--非高斯特性研究[J]. 实验流体力学, 2010, 24(3): 12-18. KE Shitang, GE Yaojun, ZHAO Lin. Research on features of fluctuating wind pressure on large hyperbolic cooling tower: features of non-Gaussian[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(3): 12-18. |
| [12] |
柯世堂, 赵林, 邵亚会, 等. Wavelet_Huang和Hilbert_Huang方法用于非高斯风压信号分析的比较研究[J]. 土木工程学报, 2011, 44(6): 61-67. KE Shitang, ZHAO Lin, SHAO Yahui, et al. Comparasion of WHT and HHT methods for analyzing non-Gaussian wind pressure signals[J]. China Civil Engineering Journal, 2011, 44(6): 61-67. |
| [13] |
CHENG X X, ZHAO L, GE Y J, et al. Wind pressures on a large cooling tower[J]. Advances in Structural Engineering, 2015, 18(2): 201-220. DOI:10.1260/1369-4332.18.2.201 |
| [14] |
KE S T, GE Y J. Extreme wind pressures and non-Gaussian characteristics for super-large hyperbolic cooling towers considering aeroelastic effect[J]. Journal of Engineering Mechanics, 2015, 141(7): 04015010. DOI:10.1061/(ASCE)EM.1943-7889.0000922 |
| [15] |
刘宇飞, 辛克贵, 樊健生, 等. 环境激励下结构模态参数识别方法综述[J]. 工程力学, 2014, 31(4): 46-53. LIU Yufei, XIN Kegui, FAN Jiansheng, et al. A review of structure modal identification methods through ambient excitation[J]. Engineering Mechanics, 2014, 31(4): 46-53. |
| [16] |
罗钧, 刘纲, 黄宗明. 基于随机减量法的非平稳激励下模态参数识别[J]. 振动与冲击, 2015, 34(21): 19-24, 64. LUO Jun, LIU Gang, HUANG Zongming. Modal parametric identification under non-stationary excitation based on random decrement method[J]. Journal of Vibration and Shock, 2015, 34(21): 19-24, 64. |
| [17] |
韩建平, 李达文. 基于Hilbert-Huang变换和自然激励技术的模态参数识别[J]. 工程力学, 2010, 27(8): 54-59. HAN Jianping, LI Dawen. Modal parameter identification based on Hilbert-huang transform and natural excitation technique[J]. Engineering Mechanics, 2010, 27(8): 54-59. |
| [18] |
杨佑发, 李帅, 李海龙. 环境激励下结构模态参数识别的改进ITD法[J]. 振动与冲击, 2014, 33(1): 194-199. YANG Youfa, LI Shuai, LI Hailong. Improved ITD method for structural modal parameter identification under ambient excitation[J]. Jornal of Cibration and Shock, 2014, 33(1): 194-199. |
| [19] |
王海军, 郑韩慈, 周济芳. 水电站厂房结构密集模态识别研究[J]. 水力发电学报, 2016, 35(2): 117-123. WANG Haijun, ZHENG Hanci, ZHOU Jifang. Study on modal identification of powerhouse strctures with closely spaced modes[J]. Journal of Hydroelectric Engineering, 2016, 35(2): 117-123. DOI:10.11660/slfdxb.20160214 |
| [20] |
郇滢, 兰惠清, 林楠, 等. 基于小波变换的GM(1, 1)-ARMA组合预测模型对悬索管桥的应变预测[J]. 应用科学学报, 2016, 34(1): 95-105. XUN Ying, LAN Huiqing, LIN Nan, et al. Prediction of suspension pipeline strain by GM(1, 1)-ARMA modal based on wavelet transform[J]. Journal of Applied Sciences-Electronics and Information Engineering, 2016, 34(1): 95-105. |
| [21] |
建筑结构荷载规范: GB 50009-2012[S]. 北京: 中国建筑工业出版社, 2012. Load code for the designs of buildingstructures: GB 50009-2012[S]. Beijing: China Architecture & Building Press, 2012. |
| [22] |
WINNEY P E. The modal properties of model and full scale cooling towers[J]. Journal of Sound & Vibration, 1978, 57(1): 131-148. |
| [23] |
曾森, 高龙涛, 陈少峰, 等. 钢管混凝土拱桥多振型组合pushover方法可行性例证[J]. 土木工程学报, 2016, 49(1): 80-85. ZENG Sen, GAO Longtao, CHEN Shaofeng, et al. Example verification of the feasibility of multi-modal pushover method for concrete-filled steel tube arch bridges[J]. China Civil Engineering Journal, 2016, 49(1): 80-85. |
| [24] |
DAVENPORT A G. Note on the distribution of the largest value of a random function with application to gust loading[J]. Proceedings of the Institute of Civil Engineers, 1964, 28(2): 187-196. DOI:10.1680/iicep.1964.10112 |
| [25] |
SADEK F, SIMIU E. Peak non-Gaussian wind effects for database-assisted low-rise building design[J]. Journal of Engineering Mechanics, 2002, 128(5): 530-539. DOI:10.1061/(ASCE)0733-9399(2002)128:5(530) |
| [26] |
柯世堂, 朱鹏, 余玮, 等. 冷却塔阻尼特性研究报告[R]. 南京: 南京航空航天大学, 2016. KE Shitang, ZHU Peng, YU Wei, et al. Research study of damping characteristics for cooling towers[R]. Nanjing: Nanjing University of aeronautics and astronautics, 2016. |
| [27] |
柯世堂, 赵林, 葛耀君. 大型双曲冷却塔表面脉动风压随机特性--风压极值探讨[J]. 实验流体力学, 2010, 24(4): 7-12. KE Shitang, ZHAO Lin, GE Yaojun. Research on features of fluctuating wind pressure on large hyperbolic cooling tower: discussions on extreme wind pressure[J]. Journal of Experiments in Fluid Mechanics, 2010, 24(4): 7-12. |
 2018, Vol. 50
2018, Vol. 50