2. 德克萨斯理工大学 土木与环境工程系,德克萨斯州拉伯克,TX 9409
2. Department of Civil and Environmental Engineering, Texas Tech University, Lubbock, TX 9409, U.S.A
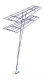
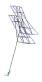
当前,随着城市化进程,大型单立柱广告牌作为新型户外媒体结构,已被广泛建造于市区、高速公路以及铁路的周边.广告牌结构由上部面板结构和单立支撑柱两部分组成.通常设计中,立柱采用焊接钢管,上部面板支撑结构是由各种型钢构件组装成的桁架或型钢框架.在中国,其结构形式发展为双面和三面两种,总高度可达30 m以上,上部面板宽达20 m,高可达10 m.由于这种结构高耸、轻柔、牌面迎风面积大,风荷载集中作用在上部牌面,整个结构的荷载和质量都呈现出头重脚轻的特点,风振响应往往显著,因此,已成为一类典型的城市风易损性结构.近年来,有关其强风作用下的破坏及次生灾害的报道屡见不鲜,已经引起研究者的关注[1-2].经过大量灾害调查,将单立柱广告牌风致破坏模式分为:面板蒙皮撕裂、面板支撑结构的屈曲、单立柱的失稳或整体倾覆三类[3-4],如图 1所示.

|
图 1 大型户外广告牌的3种典型风灾破坏模式 Figure 1 Three typical failure modes of large billboards |
目前,国内外关于刚性的低矮户外单面板广告牌结构风荷载特性研究已经比较成熟.20世纪90年代,Letchford等[5-6]通过风洞试验研究得到了不同高宽比、净空率和孔隙率的单面板广告牌的阻力和表面法向风压系数,并被多个国家的抗风设计规范所采纳[7-8].中国也结合建筑结构风荷载规范给出了单面广告牌的抗风设计方法[9-10].近年来,Warnitchai等[11]通过对单面板和双面板广告牌的风洞测力试验的比较研究,详细讨论了阻力系数、偏心距随风向角变化.Smith等[12-13]针对美国常见的低矮实体液晶面板广告牌进行了现场实测和刚性测力风洞试验,并把二者的试验结果进行了对比研究.顾明等[14-15]进行了双面和三面广告牌风洞测压试验研究,给出各面板内外两侧的风压分布特性;并通过有限元模拟计算了广告牌的风振响应.Wang等[16]针对强风下的面板撕裂破坏,通过测压试验,详细讨论了双、三面广告牌各面板净风压力及其极值的分布特征.Meyer等[17]对一横跨高速公路的箱型广告牌的涡振和驰振进行了气弹风洞试验研究.
综上所述,相对于中国广告牌应用的迅速发展,现有的广告牌风荷载计算及设计方法有待完善,尤其缺乏面板气动力荷载特征,以及整体风振动力响应规律的试验研究.鉴于此,本文选取代表性的双面广告牌结构作为研究对象,通过刚性模型的面板测压风洞试验和气动弹性模型的高频天平测力风洞试验,系统性地研究了双面广告牌上部面板结构的气动力荷载及整体结构的风振响应规律.为大型广告牌结构的风荷载计算和抗风设计提供理论依据和数据支撑.
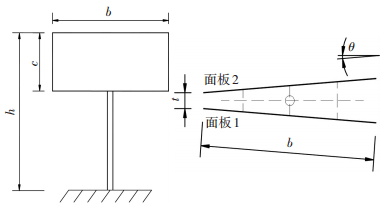
1 刚性模型的面板测压风洞试验 1.1 刚性模型设计根据中国建筑标准设计研究院《户外钢结构独立柱广告牌图集》[18]选取具有代表性的双面G2-5×14型广告牌作为本次试验的对象,结构高度为18 m.广告牌结构立面和平面图见图 2;模型缩尺比为1:20,模型上部结构面板长、宽、结构整体高度以及面板之间的夹角列于表 1.
|
图 2 双面广告牌结构示意 Figure 2 Elevation and top view of model of two-plate billboard |
| 表 1 广告牌模型结构尺寸 Table 1 Structural size of two-plate billboard model |
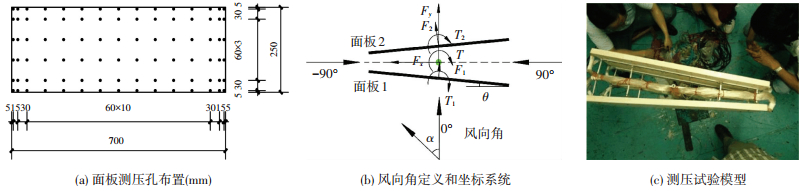
刚性测压模型中,面板由轻质松木制作而成.立柱采用直径为40 mm粗的刚性圆截面铝合金杆与法兰盘底座焊接,再固定于风洞转盘中心.测压模型结构具备足够的结构刚度.考虑到风压分布在气流分离处的变化,面板测点布置采取了边密中疏、对称满布的方式.为获得真实的面板净风压力分布,每个面板两侧表面上测压孔的位置保持一致布置了90个测点,总测点数为90×4=360个,如图 3(a)所示.试验在同济大学土木工程防灾国家重点实验室大气边界层风洞中进行.风压扫描阀采样频率为300 Hz,每个工况的采样时长为135 s,对应的实际采样时长约为10 min.试验模型见图 3(c).试验风速为10 m/s,风洞试验风场平均风和湍流度剖面见图 4,面板中心高度处的风速湍流度为9%.考虑结构对称性,测压试验风向角为-90°至90°,增量为15°,共13个风向角,如图 3(b)所示.
|
图 3 广告牌测压模型 Figure 3 Pressure test of rigid model |

|
图 4 平均风和湍流度剖面 Figure 4 Mean wind speed profile and longitudinal turbulence intensity profile |
基于测压数据,规定测点压力以指向板面为正,背离板面为负,取面板上内外两侧相同位置测点压力差为该点的净风压.力的坐标系统如图 3(b)所示.单个面板力系数和扭矩系数定义为:
| $ \begin{array}{l} {C_{{F_i}}}\left( t \right) = \sum\limits_{j = 1}^n {{p_{ij}}\left( t \right){A_{ij}}/\left( {0.5\rho U_{{\rm{ref}}}^2bc} \right)} {\rm{ }},\\ {C_{{T_i}}}\left( t \right) = \sum\limits_{j = 1}^n {{p_{ij}}\left( t \right){A_{ij}}{d_{ij}}/(0.5\rho U_{{\rm{ref}}}^2{b^2}c)} . \end{array} $ | (1) |
式中:pij(t)为第i个面板的第j个测压孔的净压力(i=1~2,j=1~90),ρ为空气密度,Uref为参考高度100 cm处的平均风速,Aij和dij分别为测点从属面积和测点i到面板竖向中轴线的力臂,b和c分别为面板的宽度和高度.
由各面板力系数,通过图 3(b)所示力的坐标系和式(2)可以得到面板结构的平行面板方向(x向)、垂直面板方向(y向)以及扭转方向的风力系数CFx、CFy及CT.
| $ \begin{array}{l} {C_{Fx}}\left( t \right) = \left( {{C_{{F_2}}}\left( t \right) - {C_{{F_1}}}\left( t \right)} \right){\rm{sin}}\theta ,\\ {C_{Fy}}\left( t \right) = \left( {{C_{{F_1}}}\left( t \right) + {C_{{F_2}}}\left( t \right)} \right){\rm{cos}}\theta ,\\ {C_T}\left( t \right) = \sum\limits_{i = 1}^2 {{C_{{T_i}}}\left( t \right)} . \end{array} $ | (2) |
水平合力系数CF(t)可由CFx、CFy得到
| $ {C_F}\left( t \right) = \sqrt {C_{Fx}^2\left( t \right) + C_{Fy}^2\left( t \right)} . $ | (3) |
面板水平风力系数,包括CFx、CFy及二者的合力系数CF,以及扭矩风力系数CT的均值、均方根和极值如图 5(a)~(d)所示,其中极值的计算采用Davenport[27]提出的峰值因子法.峰值因子的计算公式为
| $ {g_{{C_F}}} = \sqrt {2{\rm{ln}}({\nu _0}T)} + 0.577\;2/\sqrt {2{\rm{ln}}({\nu _0}T)} , $ | (4) |
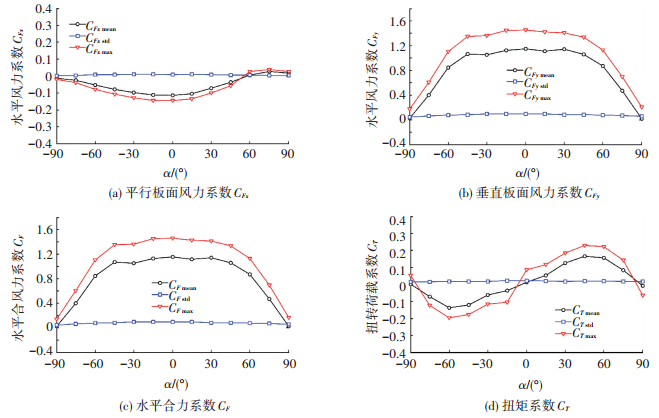
|
图 5 风力系数随风向角变化曲线 Figure 5 Wind force coefficients of two-plate configuration versus wind direction |
式中:ν0=[∫0∞n2SCF(n)dn/∫0∞SCF(n)dn]1/2为平均穿越率,T为采样时长,SCF(n)为风力系数时程的功率谱密度.可以发现,垂直面板方向风力系数CFy的均值、均方根和极值在-45°~45°风向角范围内变化不大,在0°风向角时达到最大,分别为1.15、0.09和1.45,对应的峰值因子为3.3.相对于垂直面板方向风力,平行面板方向风力系数总体上偏小.由图 5(c)可知水平合力系数CF的数值和变化规律与垂直面板方向风力系数CFy几乎相同,表明平行面板方向风力的作用可以忽略.扭矩系数较大值发生在±(45°~60°)范围内,最大扭矩系数的均值、均方根和极值分别为0.17、0.02和0.23,对应的峰值因子为3.2.上述面板结构的风力系数的结果与文献[11, 13]中的试验结果均能吻合较好.
在设计中,作用在整体结构上的扭矩,通常以作用力的偏心表示,定义水平合力的偏心系数为
| $ e\left( t \right) = {C_T}\left( t \right)/{C_F}\left( t \right). $ | (5) |
参照现有各国规范中低矮刚性单板结构的设计方法,针对实际中可能出现的低矮刚性双面广告牌结构的立柱设计,考虑两种最不利荷载状态[7-8, 19],如图 6所示.最大合力系数CF max=1.42及对应时刻的扭矩系数CT corr,此时emin为0.01, 出现风向角为0°;最大扭矩系数CT max=0.22及对应时刻的合力系数CF corr=0.95,此时emax为0.23,出现风向角为60°.
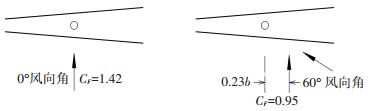
|
图 6 刚性立柱广告牌两种最不利风荷载示意 Figure 6 Two unfavorable wind load cases on plates |
此外,针对广告牌面板的支撑结构的设计,在上述两种最不利状态下,对两个面板上的平均风压系数做简化和近似,分布见图 7.
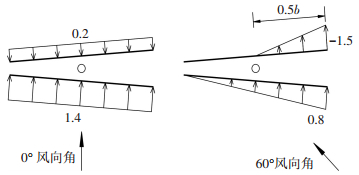
|
图 7 0°和60°风向角时面板的净压分布 Figure 7 Net pressure on plates in 0° and 60° wind directions |
与封闭的实体建筑不同,广告牌这类开敞的板式结构,在0°风向角下,背风面板受到压力而不是吸力.这与前后板面的大小及间距有关.一些高层建筑风洞测压试验也表明,在正面来风工况下,屋顶平台的背风处围护墙面的风压有可能会为正值.将上述系数与中国现有风荷载规范中阵风系数公式结合,即可分别按上述两种最不利工况计算双面广告牌面板支撑结构及刚性立柱的水平及扭转风荷载.
1.4 风荷载功率谱分析不同风向角下垂直面板方向风力系数CFy的功率谱如图 8(a)所示.横坐标为折减频率, 其中B=bcos α, 基于0°风向角下风荷载的气动导纳χa(n),风力系数功率谱可表示为
| $ {S_{{C_{Fy}}}}\left( n \right) = (4C_{Fy\;{\rm{mean}}}^2/U_{{\rm{ref}}}^2)\chi _a^2\left( n \right){S_u}\left( n \right), $ | (6) |
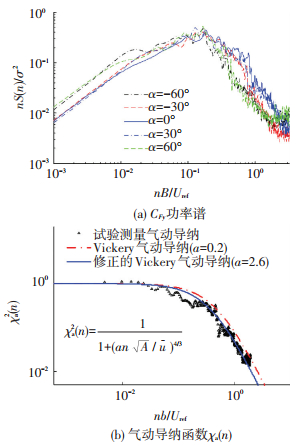
|
图 8 垂直面板方向风荷载 Figure 8 Properties of wind load perpendicular to plates |
式中Su(n)为纵向脉动风速谱.由式(6)可计算得到气动导纳函数χa(n).将之与Vickery气动导纳函数(参数a=2)比较如图 8(b)所示,A=bc为面板迎风面积,可以发现试验中导纳稍为偏低,该结论与文献[11]的结论一致.改变参数(a=2.6)对Vickery气动导纳函数进行修正,可以得到与试验结果更为切合的导纳函数.
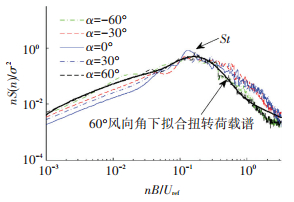
图 9给出了不同风向角下的矩扭系数谱.可以发现,在0°风向角附近时,双面广告牌的扭矩谱在折减频率0.13附近有明显的谱峰出现,与单面板的斯托罗哈数St (Strouhal number) 0.145[20]略有不同.一般来说,结构扭转荷载由湍流和脱落漩涡及尾流再附引起,对于广告牌结构,在扭转荷载较大的偏角范围-60°~60°之间,因结构深宽比不大,尾流再附引起的高频部分贡献微小.针对最大扭矩荷载出现在60°风向角,扭矩功率谱可拟合为
| $ \begin{array}{l} \frac{{n{S_T}\left( n \right)}}{{\sigma _T^2}} = \frac{{{{\left( {n/{n_{\rm{f}}}} \right)}^\mu }}}{{{{\left[ {1 - {{\left( {n/{n_{\rm{f}}}} \right)}^2}} \right]}^2} + \beta {{\left( {n/{n_{\rm{f}}}} \right)}^2}}} + \\ \quad \quad \frac{\gamma }{{\sqrt \pi }}{\rm{exp}}( - {\left[ {\frac{{{\delta ^2} - {\rm{ln}}(n/{n_{\rm{s}}})}}{\delta }} \right]^2}), \end{array} $ | (7) |
|
图 9 CT功率谱 Figure 9 PSDs of CT |
式中:右侧第一项为湍流贡献的低频段部分,采用频响函数形式[21-24];第二项为漩涡脱落频率附近部分,采用Gauss正态分布函数的形式[21-22, 24-26];其中,ns为漩涡脱落频率,nf为低频峰值对应频率,系数β、δ为带宽参数,δ与纵向湍流有关,β与结构深宽比有关,μ、γ为峰值调整系数.考虑到60°风向角时面板迎风面宽度以及前述St可以得到,ns=2.74.根据式(7)拟合得到系数nf=0.20,μ=3.03、β=30.2,γ=0.85,δ=0.76.图 9给出的拟合扭矩谱与试验谱二者吻合良好.
2 气弹模型高频天平测力风洞试验 2.1 气弹模型设计对于常见的柔性单立柱广告牌结构,本文进一步采用气弹模型风洞试验深入研究其风振动力响应.原型结构的有限元动力特性分析表明,标准图集[18]给出的结构设计合理,整体性较好,前五阶振型均未发现局部振动,结构的刚度由主体结构提供.基于此,气弹模型设计时候进行了合理简化,采用铝合金材料焊接制作模型骨架,骨架截面按照主体结构杆件刚度相似准则计算得到.质量不足通过均匀布置铅丝配重来实现.广告牌面板蒙皮实际中一般采用纤维布或者铝制的蒙皮,这里采用轻质的松木板进行模拟,固定于骨架.模型各项缩尺比参数见表 2.实际原型和模型的有限元动力特性对比见表 3.表明无论是振型还是频率,都能很好吻合.模型实际的频率及结构阻尼也在表 3中给出.相对于实际结构(阻尼通常为1%~3%),气弹模型结构阻尼偏小,其中主要振动方向(垂直板面方向)的阻尼为8.4‰,本次气弹动力试验结果偏于保守.
| 表 2 模型各物理参数缩尺比 Table 2 Physical parameters scaling of model type |
| 表 3 双面广告牌动力特性 Table 3 Dynamic characteristics of two-plate billboard |
试验采用美国ATI公司的Delta F/T六分力高频动态测力天平测得模型立柱底部各方向力,天平放置在风洞转盘中心,通过螺母把天平和立柱底部的法兰盘刚性连接,试验模型如图 10所示.测力天平信号采集系统的采样频率为200 Hz.试验风向角为-90°~90°,增量为30°,共7个风向角,力的坐标系和风向角示意与前图 3(b)一致.

|
图 10 气弹模型风洞试验 Figure 10 Wind tunnel test of aero-elastic model |
此外,上述动力分析表明,由于面板结构质量集中在两侧对称的面板和长边主梁上,虽然左右两侧短向横梁的质量不同,如图 2所示,但由于面板9°的夹角较小,两者差异很小.因此,认为结构质心与扭转刚度中心基本重合,都位于立柱的中心.
2.2 试验数据分析利用天平测得基底各方向内力响应时程,可以得到各剪力对应的力系数:
| $ \begin{array}{l} {C_{Vx}}\left( t \right) = {V_x}\left( t \right)/\left( {0.5\rho U_{{\rm{ref}}}^2bc} \right),\\ {C_{Vy}}\left( t \right) = {V_y}\left( t \right)/(0.5\rho U_{{\rm{ref}}}^2bc),\\ {C_{Tr}}\left( t \right) = {T_r}\left( t \right)/(0.5\rho U_{{\rm{ref}}}^2{b^2}c). \end{array} $ | (8) |
式中:Vx为平行面板方向基底剪力,Vy为垂直面板方向基底剪力,Tr为基底扭矩.
基底水平合剪力系数CV可由CVx、CVy得到
| $ {C_V}\left( t \right) = \sqrt {C_{Vx}^2\left( t \right) + C_{Vy}^2\left( t \right)} . $ | (9) |
图 11给出了Vx、Vy和Tr的均值、均方根、极值系数随风向角变化规律.为便于比较,将前节刚性模型测压试验的风力系数的均值结果也一并绘制在该图中.

|
图 11 风振基底响应力系数 Figure 11 Coefficients of wind-induced force response at the column bottom |
结果分析表明,垂直面板方向基底剪力系数CVy的均值与刚性测压试验得到的平均风力系数CFy分布规律非常吻合,最大均值为1.20;极值出现在0°风向角,约为1.80.平行面板方向的CVx与测压试验的结果CFx趋势有所不同,主要由于测压试验是对面板法向压力的测量,而对平行板面表面摩擦力产生的风荷载难以测出,所以存在着一定偏差,并且风向角越靠近±90°,此偏差越明显.此外,基底水平合剪力系数CV与垂直面板方向基底剪力系数CVy几乎相同,表明平行面板方向基底剪力对水平合剪力的贡献不大,这与前述测压试验得到的合风力系数表现是一致的.同样,基底扭矩风振响应也表现出与测压试验风力系数的高度一致性.扭矩响应的均值与极值在60°风向角时达最大,分别为0.20和0.39.
2.4 基底反力功率谱分析图 12(a)、(b)给出了不同风向角下垂直面板方向剪力系数CVy和扭矩系数CTr的功率谱,可以发现,由于阻尼较小,结构气弹响应的共振响应显著,其中又以各向的第一阶模态响应为主,此结论与文献[15]中广告牌垂直面板方向和扭转风振响应的数值结果一致.如前风力系数的研究所述,相对于脉动风引起的垂直面板方向抖振力荷载,扭矩风力荷载的形成更为复杂,其功率谱的低频段随风向角不同存在较大的差异,因此,基底扭矩的风振响应功率谱的背景部分差异较大.通过式(4)可以计算基底反力响应的峰值因子,结果表明各风向角下垂直面板方向剪力系数CVy和扭矩系数CTr的峰值因子均在3.0~3.5, 其中扭矩系数峰值因子基本不随风向角变化,约为3.3.

|
图 12 基底反力功率谱 Figure 12 PSDs of the column bottom response |
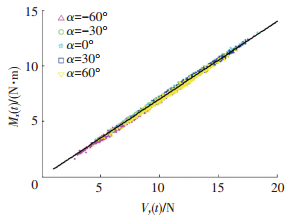
为分析风振基底弯矩的动力响应,图 13给出了各风向角下所有时刻垂直面板方向基底剪力Vy(t)与对应的平行面板方向弯矩Mx(t)的散点图,可见二者存在显著的线性相关,其拟合斜率为0.7,即与面板中心离地高度Hc=h-0.5c=0.72 m接近.基于以上分析,对于悬臂的单立柱广告牌结构,可以把整体结构视为在垂直面板方向及扭转方向分别以第一阶频率的结构来进行风振响应的分析和计算.基底剪力的响应与对应弯矩响应具有同步一致性.
|
图 13 不同风向角下Vy(t)~Mx(t)散点图 Figure 13 Scatter plot of Vy(t)~Mx(t) in different wind directions |
如前所述,气弹动力响应的基底反力的均值系数与前述测压试验风荷载力均值系数的比较可以发现,除了可以忽略的平行面板方向之外,垂直面板方向、水平方向合力、扭矩响应均表现出良好的一致性.由于整个结构的风荷载和质量都集中在上部面板结构上.作为悬臂的单立柱支撑结构,其侧移和扭转刚度由单立柱提供.因此,广告牌结构的风振动力学模型可简化为上部结构以两个水平方向和一个扭转向以基阶振型振动的三自由度体系.且由于对称性,刚心和质量中心一致,可不考虑各方向运动的耦合.
3.1 垂直面板方向风振响应为分析结构风振气动阻尼,在0°最不利风向角下垂直面板方向风振响应的准定常气动阻尼比ζaero理论值为
| $ {\zeta _{{\rm{aero}}}} = (\frac{{{C_{Fy\;{\rm{mean}}}}}}{{4\pi }})\left( {\frac{{\rho Ab}}{m}} \right)/(\frac{{b{n_0}}}{{\bar u}}), $ | (10) |
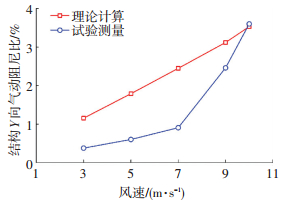
式中:ρAb/m为质量比,bn0/u为折减频率,m为上部结构总质量,n0为自振频率.利用随机减量法(RDT)对不同风速下垂直面板方向基底剪力CVy的气动阻尼进行识别和提取,与理论公式(10)计算的结果比较如图 14所示,在试验风速10 m/s附近(对应实际风速约45 m/s)吻合.比较表 3中结构阻尼ζs,可以发现在试验风速10 m/s时,气动阻尼约为结构阻尼的4倍,因此气动阻尼对广告牌风振影响不可忽略.
|
图 14 垂直板面方向气动阻尼比 Figure 14 The aerodynamic damping ratio in 0° wind direction |
根据随机振动理论,由参考高度处脉动风速,代入z=90 cm高度处(略高于结构高度Hc)的脉动风速谱Su及对应的平均风力系数CFy mean,以此计算得到Hc处的响应位移,位移响应功率谱为:
| $ \quad {S_y}\left( n \right) = {\left| {H\left( n \right)} \right|^2}{({C_{Fy\;{\rm{mean}}}}\rho A\bar u)^2}\chi _a^2\left( n \right){S_u}\left( n \right),\\ {\left| {H\left( n \right)} \right|^2} = \frac{1}{{{m^2}{{\left( {2\pi {n_0}} \right)}^4}\left\{ {{{\left[ {1 - {{\left( {n/{n_0}} \right)}^2}} \right]}^2} + 4{\zeta ^2}{{\left( {n/{n_0}} \right)}^2}} \right\}}}. $ | (11) |
式中ζ为风振总阻尼比,ζ=ζs+ζaero.进而得到垂直面板方向基底剪力功率谱为
| $ {S_{Vy}}\left( n \right) = {[m{(2\pi {n_0})^2}]^2}{S_y}\left( n \right). $ | (12) |
则垂直面板方向基底剪力均方根为
| $ {\sigma _{Vy}} = \sqrt {\int_0^\infty {{S_{Vy}}\left( n \right){\rm{d}}n} } . $ | (13) |
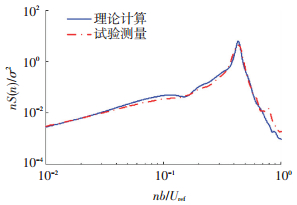
图 15给出了按式(12)代入试验测量气动导纳和阻尼得到SVy的理论结果,与试验测量结果吻合.事实上,考虑试验测量气动导纳的频域非定常理论计算方法与将风压时程荷载作用于结构的时域非平稳响应的计算方法一致.响应均方根系数及其背景和共振分量(分别用B和R表示)在表 4中列出.结果显示,考虑气动导纳和气动阻尼的抖振响应理论计算方法可以与气弹试验的结果吻合较好.理论方法的精度主要取决于气动导纳和气动阻尼取值的准确性.
|
图 15 垂直面板方向的基底剪力系数功率谱 Figure 15 The PSDs of shear force coefficient at the column bottom in 0° wind direction |
| 表 4 垂直面板方向基底剪力系数CVy均方根 Table 4 The RMS of shear force coefficient at the column bottom in 0° wind direction |
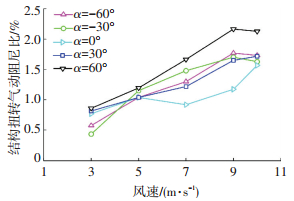
对不同风速、风向下扭矩风振响应的气动阻尼比进行识别和提取,如图 16所示.同样,可以发现结构阻尼比气动阻尼小,后者对广告牌扭转风振影响不可忽略.
|
图 16 扭转气动阻尼比 Figure 16 Torsional aerodynamic damping ratio |
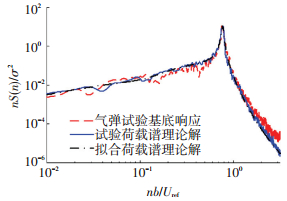
同样,运用式(11)~(13), 分别代入刚性模型试验中的扭转荷载谱和拟合扭转荷载谱,采用图 16中的扭转气动阻尼,计算了扭转最不利60°风向角、试验风速10 m/s工况的基底扭矩响应CTr的功率谱.图 17给出了上述二者结果与气弹试验功率谱的比较,表 5列出了三者均方根的比较.可以发现,理论计算与气弹试验测量结果吻合.理论计算的精度取决于气动阻尼.
|
图 17 60°风向角扭矩系数功率谱 Figure 17 The PSDs of torsional moment coefficient at the column bottom in 60° wind direction |
| 表 5 60°风向角时扭矩系数CTr均方根 Table 5 The RMS of torsional moment coefficient in 60° wind direction |
1) 垂直面板方向基底剪力系数和水平合剪力系数及基底扭矩系数的均值与刚性模型测力试验结果基本一致.水平风荷载及风振响应均以垂直面板方向为主.平行面板方向响应及荷载可以忽略.垂直面板方向及扭转风荷载最不利风向角分别出现在0°和60°.基于此,给出了刚性立柱及面板支撑结构的风荷载的建议计算方法.
2) 气弹性动力试验表明,对于柔性悬臂的单立柱广告牌结构,风振响应的共振分量显著.整体结构可视为在垂直面板方向和扭转方向分别以第一阶频率的集中质点结构来进行风振响应的分析和计算.
3) 在计算垂直面板方向理论风荷载谱时建议考虑气动导纳的影响;在拟合扭转荷载谱时需要考虑低频湍流和高频漩涡脱落激励的贡献.考虑气动阻尼后,利用理论方法计算的风振响应与气弹动力试验的结果能吻合.理论方法的精度主要取决于气动导纳和气动阻尼取值的准确性.
本研究为完善大型广告牌结构的抗风设计,提供了风荷载计算理论方法的探索及风洞试验数据的支撑.
| [1] |
安水晶. 单立柱广告牌结构风灾易损性研究[D]. 哈尔滨: 哈尔滨工业大学, 2009. AN Shuijing. Wind disaster vulnerability study of single-column billboard structure[D]. Harbin: Harbin Institute of Technology, Harbin, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10213-2010026430.htm |
| [2] |
TAMURA Y, CAO Shuyang. Climate change and wind-related disaster risk reduction[C]// Proceedings of the APCWE-Ⅶ. Taipei, Taiwan: [s. n. ], 2009.
|
| [3] |
宋芳芳, 欧进萍. 城市巨型广告牌台风损伤成因与动力分析[C]//第十四届全国结构风工程学术会议论文集. 北京: 中国建筑科学研究院, 2009: 829-834. SONG Fangfang, OU Jinping. Study on the dynamic causes of damage of large billboard by typhoon[C]//14th National Conference of Structural Wind Engineering. Beijing: China Academy of Building Research, 2009: 829-834. |
| [4] |
宋芳芳, 欧进萍. 台风"黑格比"对城市建筑物破坏调查与成因分析[J]. 自然灾害学报, 2010(4): 8-16. SONG Fangfang, OU Jinping. Investigation and analysis of structures damage caused by typhoon Hagubit[J]. Journal of Natural Disasters, 2010(4): 8-16. DOI:10.13577/j.jnd.2010.0402 |
| [5] |
LETCHFORD C W, HOMELS J D. Wind loads on free-standing walls in turbulent boundary layers[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1994, 51: 1-27. DOI:10.1016/0167-6105(94)90074-4 |
| [6] |
LETCHFORD C W. Wind loads on rectangular signboards and hoardings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89: 135-151. DOI:10.1016/S0167-6105(00)00068-4 |
| [7] |
Minimum design loads for buildings and other structures: ASCE/SEI 7-10[S]. Reston: VA, 2010.
|
| [8] |
Structural Design Actions Part 2: Wind actions: AS/NZS 1170. 0: 2011[S]. Sydney & Wellington: Standards Australia Limited & Standards New Zealand, 2011.
|
| [9] |
户外广告设施钢结构技术规程: CECS 148-2003[S]. 北京: 中国建筑工业出版社, 2003. Technical specification for steel structures of outdoor advertisement facility: CECS 148-2003[S]. Beijing: China Architecture & Building Press, 2003. |
| [10] |
建筑结构荷载规范: GB 50009-2012[S]. 北京: 中国建筑工业出版社, 2012. Load code for the design of building structures: GB 50009-2012[S]. Beijing: China Architecture & Building Press, 2003. |
| [11] |
WARNITCHI P, SINTHUWONG S. Wind tunnel model test of large billboards[J]. Advance in Structural Engineering, 2009, 12(1): 103-109. DOI:10.1260/136943309787522650 |
| [12] |
SMITH D A, ZUO D L, MEHTA. Characteristics of wind induced net force and torque on a rectangular sign measured in the field[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 133: 80-91. DOI:10.1016/j.jweia.2014.07.010 |
| [13] |
ZUO D L, SMITH D A, MEHTA. Experimental study of wind loading of rectangular sign structures[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2014, 130: 62-74. |
| [14] |
顾明, 陆文强, 韩志惠, 等. 大型户外独立柱广告牌风压分布特性[J]. 同济大学学报(自然科学版), 2015, 43(3): 337-344. GU Ming, LU Wenqiang, HAN Zhihui, et al. Characteristics of wind pressure distribution on large single column supported billboards,[J]. Journal of Tongji University (Natural Science), 2015, 43(3): 337-344. DOI:10.11908/j.issn.0253.374x.2015.03.003 |
| [15] |
韩志惠, 顾明. 大型户外独立柱广告牌风致响应及风振系数分析[J]. 振动冲击, 2015, 34(19): 131-137. HAN Zhihui, GU Ming. Wind-induced response and wind vibration coefficient of large single column-supported billboards[J]. Journal of Vibration and Shock, 2015, 34(19): 131-137. |
| [16] |
WANG Dahai, CHEN Xinzhong, LI Jie, et al. Wind load characteristics of large billboard structures with two-plate and three-plate configurations[J]. Wind and Structures, 2016, 22(6): 703-721. DOI:10.12989/was.2016.22.6.703 |
| [17] |
MEYER D, CHOWDHURY A G, IRWIN P. Investigation of wind-induced dynamic and aeroelastic effects on variable message signs[J]. Wind & Structures An International Journal, 2015, 20(6): 793-8. |
| [18] |
户外钢结构独立柱广告牌图集: 07SG 526-2007[S]. 北京: 中国计划出版社, 2007. Collective drawing of outdoor steel structure advertisement board supported by single column: 07SG 526-2007[S]. Beijing: China Planning Press, 2007. |
| [19] |
MOHAMED E, KHALED G, TED S. Torsional and shear wind loads on flat-roofed building[J]. Engineering Structure, 2015, 84(3): 313-324. |
| [20] |
SIMIU E, SCANLAN R H. Wind effects on structures. [M]. 3rd ed. New York: John Wiley and Sons, 1996: 105-106.
|
| [21] |
唐意, 顾明, 全涌. 高层建筑的扭转风荷载功率谱密度[J]. 同济大学学报(自然科学版), 2007, 35(4): 435-439. TANG Yi, GU Ming, QUAN Yong. Power spectral densities of torsional wind loads on tall buildings[J]. Journal of Tongji University (Natural Science), 2007, 35(4): 435-439. |
| [22] |
LIANG Shuguo, LI Qiusheng. Torsional dynamic wind loads on rectangular tall buildings[J]. Engineering Structure, 2004, 26: 129-137. DOI:10.1016/j.engstruct.2003.09.004 |
| [23] |
章李刚, 楼文娟, 申屠团兵. 不规则结构扭转风荷载[J]. 浙江大学学报(工学版), 2011, 45(6): 1094-1099. ZHANG Ligang, LOU Wenjuan, SHENTU Tuanbing. Torsional wind load with irregular shape[J]. Journal of Zhejiang University (Engineering Science), 2011, 45(6): 1094-1099. |
| [24] |
SOLARI G. Mathematical model to predict 3-D wind loading on building[J]. Engineering Machinery, 1985, 111(2): 254-276. |
| [25] |
KAREEM A. Model for predicting the across-wind response of buildings[J]. Engineering Structure, 1984, 6: 136-141. DOI:10.1016/0141-0296(84)90006-3 |
| [26] |
BASU R I, VICKERY B J. Across-wind vibrations of structure of circular cross-section. Part Ⅱ. Development of a mathematical model for full-scale application[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1983, 12(1): 75-97. |
| [27] |
DAVENPORT A G. Gust loading factors[J]. Journal of Structural Division, 1967, 93(3): 11-34. |
 2018, Vol. 50
2018, Vol. 50