2. 河北建筑工程学院 土木工程学院,河北 张家口 075000;
3. 哈尔滨鸿盛节能体系研发中心,哈尔滨 150036
2. School of Civil Engineering, Hebei Institute of Architecture and Civil Engineering, Zhangjiakou 075000, Hebei, China;
3. Harbin Hongsheng Building Research Energy System R&D Center, Harbin 150036, China
地震作用下,框架结构中的砌体填充墙破坏严重甚至外闪倒塌.学者们以震害调查、模型试验和理论分析等方法对框架新型墙体结构开展了大量研究.Ganesan等[1]对框架内填钢丝网水泥墙板结构进行了抗震试验;Akin等[2]对框架内填2 mm厚薄钢板结构进行了抗震对比试验与理论分析;Mohammadi[3]研究了框架带洞设摩擦滑动“保险丝”填充墙结构的抗震性能; Onat等[4]对两层框架内填带洞双页空心墙体进行了振动台试验和数值模拟;魏文晖等[5]研究了框架嵌入50 mm厚混凝土墙体结构;郭宏超等[6]进行了框架内填90 mm厚再生混凝土墙板结构抗震性能试验;陈晓等[7]对开洞柔性连接叠合填充墙板框架结构进行了抗震研究;金晓飞等[8]研究了内嵌墙板框架等效单斜撑简化模型;Asteris等[9]提出了改进宏观模型,考虑开洞和竖向荷载对结构的影响;Nasiri等[10]对框架填充墙结构进行了数值模拟与试验验证.
目前,中国相关规范、规程对剪力墙采用双排、多排配筋的要求主要是针对高层、超高层,对多层结构不尽合理.因此,课题组提出单排配筋剪力墙结构.研究表明:其抗震性能优于带端部约束配筋砖砌体[11];相同配筋率的单排配筋剪力墙与双排配筋剪力墙承载力相当而延性更好[12].课题组主编的北京地方标准正在编制中,部分成果已推广应用.
基于前期研究,提出框架内填单排配筋墙体结构.与框架内填砌体结构相比:抗侧刚度和水平承载力提高,耗能良好,后期承载力稳定;单排配筋拉结下,破坏后的墙体具有良好的平面外稳定性.以往学者多以单层结构的理论分析和数值模拟为主,框架带洞口墙体多层整体结构抗震性能试验研究较少.因此,本文对2榀带洞口、两层单跨1/2缩尺整体结构进行低周反复试验,研究洞口对钢筋混凝土框架内填单排配筋墙体结构抗震性能的影响.
1 试验概况 1.1 试件设计模型取自武汉光谷动力某建筑结构,按1/2缩尺设计并制作两榀试件,编号为KJQ3、KJQ4.KJQ3为右侧带门洞构件,门洞高1 050 mm,宽900 mm,洞口与墙体面积比0.16;KJQ4为带窗洞构件,每层对称设置两个窗洞,窗洞高600 mm,宽900 mm,洞口与墙体面积比为0.18.
试件几何尺寸、配筋及梁柱应变测点布置见图 1.两个试件的梁、柱、楼板尺寸与配筋相同.试件总高4 475 mm,一层层高1 800 mm,二层层高1 975 mm,跨度4 200 mm.洞口两侧设置暗柱,洞口上部设置暗梁,窗洞下设置洞口加强筋.暗柱截面100 mm×50 mm(宽×墙厚),暗梁截面200 mm×50 mm(高×墙厚).内填墙体采用单排配筋混凝土墙体,水平和纵向钢筋均为ϕ4@120,配筋率为0.21%.3次立模分层浇筑,在试验室内进行养护.

|
图 1 试件几何尺寸及构造 Figure 1 Dimensions and details of specimens |
试件模型采用C30细石混凝土,用料为P.O42.5硅酸盐水泥、Ⅱ级粉煤灰、S95级矿粉、中砂、粒径小于10 mm的细石、CKL聚羧酸防冻剂,质量配合比见表 1.实测一层立方体抗压强度平均值为36.65 MPa,二层为35.74 MPa.地梁采用C50普通混凝土,立方体抗压强度平均值为53.76 MPa.
| 表 1 混凝土材料用量 Table 1 Concrete mix designs per cubic meter |
梁、柱、暗梁纵筋采用

| 表 2 钢筋力学性能 Table 2 Mechanical properties of steel bars |
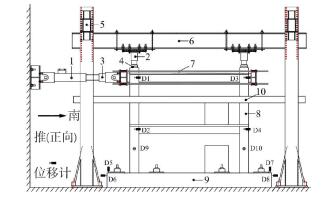
试验在中国地震局工程力学研究所恢先综合实验室内完成,加载装置见图 2.竖向千斤顶与反力梁之间设有滑动装置,试验前调整对中,保证水平侧移不受竖向加载装置的约束.在二层中部设置2道侧向支撑,支撑与试件间设置滑动滚轴, 保证试件平面外稳定.高强拉杆穿过加载端板装置固定夹紧试件,水平作动器连接试件,实现水平加载.
|
1.水平作动器;2.竖向千斤顶;3.水平荷载传感器;4.竖向荷载传感器;5.侧梁;6.反力梁;7.高强拉杆;8.试件模型;9.地梁;10.侧向支撑 图 2 加载装置 Figure 2 Text setup |
试验时,每个柱端的轴向压力为900 kN, 试验轴压比为0.21.首先施加轴向压力,加载至设计轴压力的30%后卸载,重复3次,待仪表读数正常、加载装置稳定后加至满载,并保持恒定.在距地梁顶面3 600 mm高度处施加水平荷载,预加载3次,一切正常后进行正式加载.水平加载规定以推(向右)为正,拉(向左)为负.
采用力-位移混合加载制度,屈服前按荷载控制,当骨架曲线出现明显拐点时,认为进入屈服阶段,开始按位移进行控制,每级循环一次.出现明显破坏或承载力下降到峰值的85%,停止加载.
1.4 测点布置主要测量内容包括:1)水平、竖向荷载的数值;2)层间和整体位移,距地梁顶1 625、3 600 mm高度各布置2个水平位移计;3)地梁两端布置位移计,监测水平滑移和竖向翘起;一层柱中部布置位移计,监测面外位移;4)钢筋应变测点见图 1、3(KZZ表示柱纵筋,KZG表示柱箍筋,KLZ表示梁纵筋,KLG表示梁箍筋,QH表示墙水平筋,QV表示墙纵筋,AZZ表示暗柱纵筋,AZG表示暗柱箍筋,ALZ表示暗梁纵筋,ALG表示暗梁箍筋,JQ表示窗洞加强筋).人工观测裂缝并记录损伤过程.

|
图 3 钢筋应变测点布置 Figure 3 Determination of the steel strain |
荷载控制阶段:当正向加载至82.63 kN,一层门洞角部出现裂缝;当正向加载至246.32 kN,二层出现2条45°贯穿墙面的斜裂缝;当负向加载至282.11 kN,一层墙面出现1条45°斜向贯穿裂缝,二层墙体中部形成交叉裂缝.
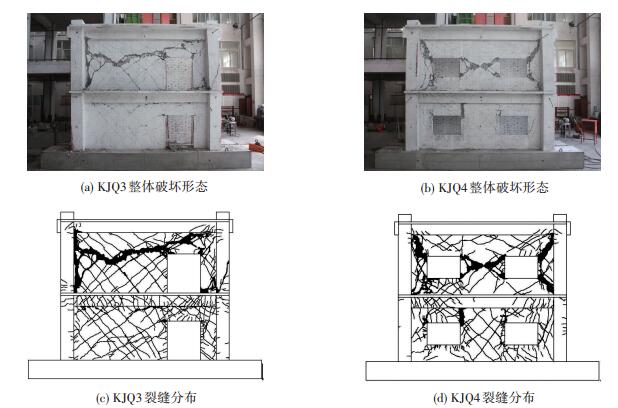
位移控制阶段:随位移增加,墙体、梁、楼板裂缝逐渐增多.当正向加载至19.43 mm(整体位移角θ=1/185),达到正向峰值785.26 kN,二层墙体与梁边、柱边裂缝较多,二层左侧数条平行的斜向贯穿墙面的裂缝宽度明显加大;当负向加载至20.81 mm(θ=1/173),达到负向峰值618.42 kN,一层、二层墙面斜裂缝宽度增大;二层门洞左上角部出现多条斜裂缝,混凝土起皮脱落;正向加载至22.03 mm(θ=1/163),二层墙体沿A柱边起皮褶皱,裂缝向二层门洞角部及上部墙体延伸,形成墙体破坏的主要区域.当负向加载至79.61 mm(θ=1/45),二层B柱斜裂缝导致柱轴力下降,考虑安全,停止加载.最终破坏形态及裂缝分布见图 4(a)、(c).
|
图 4 试件破坏形态 Figure 4 Failure patterns of specimens |
荷载控制阶段:正向加载至59.47 kN,一层北窗洞左上侧墙体出现多条裂缝;正向加载至198.95 kN,一层窗间墙出现第1条贯穿斜裂缝;正向加载至296.32 kN,二层窗间墙出现1条45°贯穿墙体的斜裂缝.正向加载至362.63 kN,有梁端钢筋屈服,此后梁端纵筋逐渐均屈服,梁端裂缝发展充分.
位移控制阶段:负向加载至5.64 mm(θ=1/638),二层窗间墙形成交叉裂缝;正向加载至8.12 mm(θ=1/443),一层窗间墙形成交叉裂缝;正向加载至13.44 mm(θ=1/268),达到正向峰值504.74 kN,墙体斜裂缝增多,梁侧裂缝增多,二层窗间墙混凝土掉渣脱落;负向加载至16.68 mm(θ=1/216),达到负向峰值545.26 kN,墙体主要裂缝已形成,一、二层梁侧面出现多条裂缝;B柱南侧水平裂缝有延伸.一层南侧梁柱节点出现2条斜裂缝.负向加载至71.25 mm(θ=1/51),墙体破坏严重,停止加载.破坏形态及裂缝分布见图 4(b)、(d).
破坏特征分析:1)内填单排配筋墙体是第一道抗震防线,墙体破坏退出工作后,框架仍具有良好的承载和变形能力; 2)洞口对墙体破坏形态影响较大.带门洞试件无洞口侧沿梁边、柱边区域形成裂缝,向右延伸与门洞上部墙体裂缝形成拉通;带窗洞墙体窗间墙、窗洞口两侧墙体破坏较严重而逐渐退出工作; 3)与框架内填砌体结构相同之处是墙体先出现裂缝,而后框架梁、柱、节点逐渐出现裂缝;不同之处为墙体多为交叉斜裂缝,框墙交界裂缝拉通后,承载力明显下降;而普通框架内填砌体结构墙体多为阶梯状交叉斜裂缝,墙角破坏严重,框墙裂缝出现较早,随荷载增大而增宽; 4)钢筋混凝土框架内填带洞口单排配筋墙体结构中,梁端的纵筋均屈服,柱端的纵筋部分屈服,梁、柱的箍筋均未屈服,框架实现了“强柱弱梁”、“强剪弱弯”、“强节点”的设计原则.
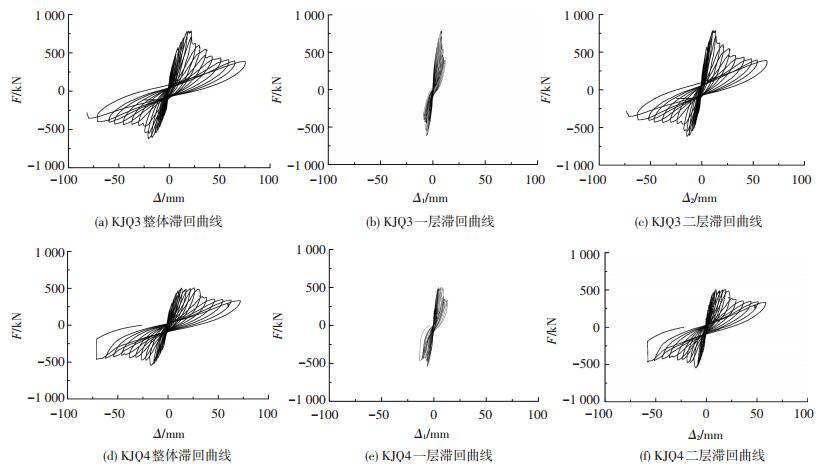
2.2 滞回性能试件水平荷载-顶部侧向位移、水平荷载-层间侧向位移的滞回曲线见图 5,图中F为顶部水平荷载,Δ为顶部加载点高度处水平位移,取顶部位移计表 1和表 3的均值,Δ1为一层层间水平位移,取一层位移计表 2和表 4的均值,Δ2为二层层间水平位移,取顶部与一层层间位移的差值.由图 5可知:
|
图 5 荷载-位移滞回曲线 Figure 5 Load-displacement hysteretic loops of specimens |
| 表 3 试件的特征荷载 Table 3 Character load of specimens |
| 表 4 KJQ3位移延性系数 Table 4 Ductility coefficient of KJQ3 |
| 表 5 KJQ4位移延性系数 Table 5 Ductility coefficient of KJQ4 |
1) 试件KJQ3的整体结构滞回曲线不对称,正向比负向的滞回曲线包围的面积大,正向比负向的承载力约高27%,表明因右侧洞口削弱墙体,导致负向承载力下降,致使滞回曲线形状不对称.
2) 试件KJQ4的整体结构滞回曲线,屈服前,滞回曲线残余变形较小;屈服后,滞回环面积逐渐增大,曲线形状由弓形向反S形发展;峰值前滞回曲线基本对称,峰值后随水平位移的增加,正向承载力在峰值处较稳定,体现了一定的延性性能.
3) 两个试件二层比一层的滞回曲线要饱满,滞回环包围的面积大,耗能较多,一层滞回曲线捏拢严重,变形较小.与试件一层侧移较小破坏较轻、二层侧移较大破坏较严重的试验现象相一致.
2.3 骨架曲线F-Δ、F-Δ1、F-Δ2骨架曲线见图 6.试件特征荷载见表 3,表 3中Fcr是墙体最初开裂时对应的荷载,Fy是按等效能量法确定的屈服荷载,Fm是实测的峰值荷载,Fu是根据峰值荷载下降到85%对应荷载确定的破坏荷载.由表 3和图 6可知:

|
图 6 骨架曲线 Figure 6 Skeleton curves of specimens |
1) 试件KJQ3、KJQ4的骨架曲线可分为弹性、屈服、峰值、下降段4个阶段.
2) 加载初期,骨架曲线为线性,试件呈弹性状态,2个试件正、负向骨架曲线分别基本重合.表明2个试件的正、负向初始刚度很相近.
3) 随荷载增加,试件进入弹塑性状态,KJQ3骨架曲线正向斜率大于KJQ4,而2个试件负向斜率几乎一致,表明峰值前,KJQ3正向刚度高于试件KJQ4,而2个试件负向刚度退化幅度基本一致.
4) 峰值后,损伤累积增加,进入下降段.2个试件骨架曲线后期承载力基本稳定,表明墙体退出工作后,逐渐演化为承载力稳定的框架结构.
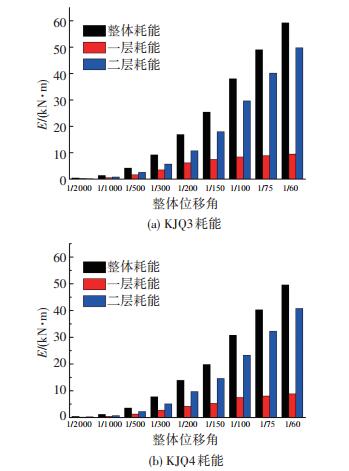
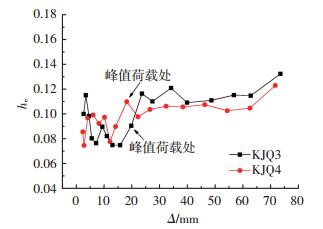
2.4 耗能能力采用骨架曲线与位移轴所围面积的耗能代表值E与等效黏滞阻尼系数he来反应结构的耗能.图 7给出了试件的耗能对比图,图 8给出了he随整体位移Δ的变化图.由图 7、8可知:
|
图 7 试件耗能对比 Figure 7 Comparison of energy dissipation |
|
图 8 等效黏滞阻尼系数 Figure 8 Equivalent viscous damping ratio |
1) 相同整体位移角时,KJQ3耗能能力高于KJQ4.当整体位移角为1/200时,KJQ3整体耗能约为KJQ4的1.22倍,当整体位移角为1/100时,KJQ3整体耗能约为KJQ4的1.24倍.
2) 整体位移角1/200之后,二层耗能增加较快,一层耗能增加缓慢.当整体位移角为1/200时,KJQ3二层耗能约占整体耗能的63.5%,KJQ4二层耗能约占整体耗能的69.8%.当整体位移角为1/100时,KJQ3二层耗能约占整体耗能的78.0%,KJQ4二层耗能约占整体耗能75.7%.表明在峰值后,水平荷载作用下,二层墙体破坏严重,变形较大,耗能较多.
3) 峰值荷载后,KJQ3、KJQ4的等效黏滞阻尼系数he比峰值前有所增大,表明峰值后墙体因破坏退出工作,试件中的框架耗能比重增加,整体结构耗能能力增强;与KJQ4相比,峰值后KJQ3的黏滞阻尼系数he略大,表明峰值后KJQ3的耗能能力略高于KJQ4.
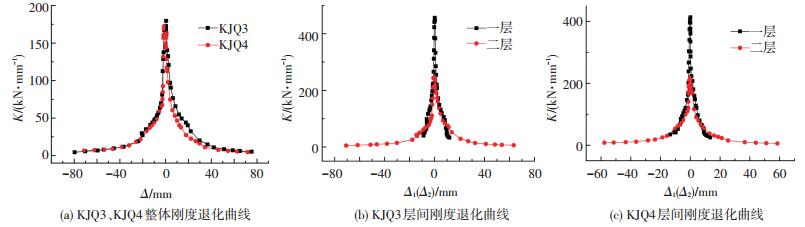
2.5 刚度退化采用各级加载峰值点的割线刚度来反映刚度的衰减变化规律,即Ki=Fi/Δi,Ki为第i级割线刚度,Fi为第i级加载的峰值荷载,Δi为第i级峰值荷载对应位移.由图 9试件整体、层间刚度退化曲线可知:
|
图 9 刚度退化曲线 Figure 9 Curves of stiffness degradation |
1) KJQ3整体结构的正向初始刚度、屈服刚度、峰值刚度,分别比负向高7.37%、30.43%、35.97%, 表明门洞使墙体初始刚度略有降低,对屈服、峰值刚度均影响较大,因破坏了墙体的整体性,屈服刚度和峰值刚度降低较多.
2) 加载前期,KJQ3的正向刚度比KJQ4要大,表明KJQ3左侧无洞口削弱,整体性较好,因而正向刚度大于KJQ4.KJQ3、KJQ4的负向刚度曲线几乎一致,表明负向加载时,两个试件的抗推刚度很接近.
3) KJQ3、KJQ4二层层间刚度小于一层层间刚度,因二层比一层高175mm,顶部水平荷载作用下,比一层水平侧移大,裂缝多,破坏严重.
4) 按公式D=1-P/k0u来计算结构的整体损伤变量[13].其中,D为结构整体损伤变量, P为外力,k0为结构初始刚度,u为与外力P对应结构位移.KJQ3正向峰值时D=0.775,负向峰值时D=0.822;KJQ4正向峰值时D=0.770,负向峰值时D=0.810.表明试件负向加载损伤较严重;墙体对初始刚度贡献比较大,峰值时墙体损坏较严重.
2.6 位移延性延性性能反映了结构屈服后的变形能力,采用位移延性系数μ=Δu/Δy来表示.表 4、5给出了试件的位移延性系数.其中,Δy为屈服位移、Δu为极限位移,μ为位移延性系数.由表 4、5可知:
1) KJQ4整体结构正向、负向位移延性系数分别为3.07、2.44,均大于KJQ3整体结构正向、负向位移延性系数2.20、1.72.KJQ4的正、负向延性系数分别比KJQ3大39.55%、41.86%.表明在洞口与墙体面积比相差不大时,对称布置窗洞比一侧带门洞的结构延性好,墙体洞口设置对延性影响较大,合理设置墙体洞口可改善结构延性.
2) KJQ3一层正向、负向的μ为1.79、1.62,二层正向、负向的μ为2.49、1.77;KJQ4一层正向、负向的μ为2.52、1.68,二层正向、负向的μ为3.35、2.94.表明2个试件二层的位移延性好于一层.
3) KJQ3整体、一层、二层结构平均延性系数分别为1.95、1.71、2.09;KJQ4整体、一层、二层结构平均延性系数分别为2.75、2.05、3.14;延性系数普遍小于3,对延性性能还需进一步研究.
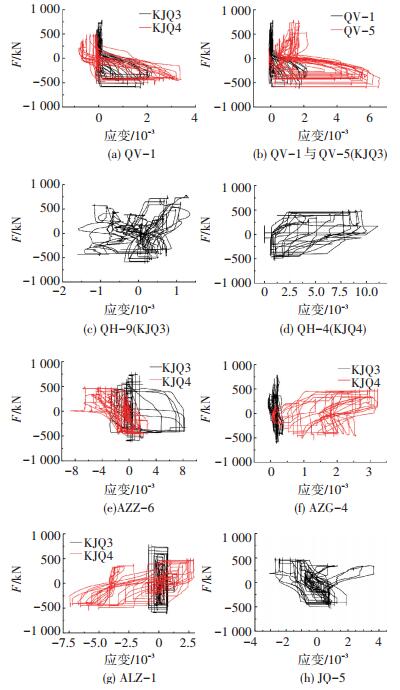
2.7 钢筋应变对单排配筋墙体钢筋和洞口周边暗柱、暗梁、窗洞下加强钢筋等典型应变测点进行分析,如图 10所示.规定拉应变为正,压应变为负.
|
图 10 钢筋应变滞回曲线 Figure 10 Hysteretic loops of strains of steel bars |
1) 2个试件墙体纵筋QV-1测点应变见图 10(a).KJQ3该点有拉有压,以拉应变为主,拉应变较大.KJQ4该点应变有拉有压,拉应变趋于屈服,表明2个试件墙体外侧纵筋的拉应变均较大.KJQ3中QV-1与QV-5测点应变对比图 10(b)中,QV-5纵筋应变较大,表明构件受拉时,门洞附近墙体底部纵筋拉应力较大,应适当加强.
2) KJQ3中QH-9测点应变见图 10(c),该测点墙体水平钢筋有拉有压但未屈服.KJQ4中QH-4测点应变见图 10(d),该测点均为拉应变,拉应变已远超屈服应变,与窗间墙墙体开裂、混凝土脱落等破坏严重的试验现象相一致.表明墙体水平钢筋在墙体开裂后,充分参与整体工作,且处于主要破坏区域的水平钢筋应变发展更充分.
2.7.2 洞口周围钢筋应变1) 暗柱纵筋AZZ-6测点应变见图 10(e).KJQ3该点后期拉应变较大,超过屈服应变1 981×10-6.KJQ4该点拉压应变均较大,后期压应变较大,受压屈服.暗柱箍筋AZG-4测点应变见图 10(f),KJQ3该点应变有拉有压,拉压均未屈服.KJQ4该点拉应变较大,超过屈服应变2 018×10-6.表明洞口角部暗柱纵筋、箍筋应力均较大,暗柱对增强洞口周边墙体的整体性、延缓洞口周边墙体破坏起到了一定作用.
2) 暗梁纵筋ALZ-1测点应变见图 10(g).KJQ3该点拉压应变较大,但均未屈服.KJQ4该点拉压均屈服,超过屈服应变2 124 ×10-6.表明洞口角部应力较大,洞口设置暗梁的必要性.KJQ4窗洞下加强筋KJQ-5应变见图 10(h),拉压应变均较大,超过屈服应变2 303 ×10-6.与二层窗洞左下角部加强筋鼓起裸露,混凝土开裂脱落,破坏严重的现象相一致.
3 结论1) 钢筋混凝土框架内填带洞口单排配筋墙体结构具有两道抗震防线,墙体是第一道抗震防线,墙体退出工作后,演化为承载力稳定的框架结构.
2) 洞口对墙体的破坏形态影响较大.无洞口侧墙体沿梁、柱边破坏;门洞上部、角部墙体破坏严重;带窗洞墙体的窗间墙、窗洞角部墙体破坏严重.
3) 洞口对水平承载力、抗侧刚度影响较大,无洞口比带门洞一侧的承载力高27%,无洞口比带门洞一侧的初始刚度、屈服刚度、峰值刚度分别高7.37%、30.43%、35.97%;洞口布置对延性系数有较大影响,对称布置窗洞试件的正、负向延性系数分别比单侧带门洞试件大39.55%、41.86%.
4) 钢筋混凝土框架内填带洞口单排配筋墙体结构中,框架实现了“强柱弱梁”、“强剪弱弯”、“强节点”的设计原则.
| [1] |
GANESAN N, INDIRA P, IRSHAD P. Effect of ferrocement infill on the strength and behavior of RCC frames under reverse cyclic loading[J]. Engineering Structures, 2017, 151: 273-281. DOI:10.1016/j.engstruct.2017.08.031 |
| [2] |
AKIN E, KORKMAZ S Z, KORKMAZ H H, et al. Rehabilitation of infilled reinforced concrete frames with thin steel plate shear walls[J]. Journal of Performance of Constructed Facilities, 2016, 30(4): 04015098. DOI:10.1061/(ASCE)CF.1943-5509.0000840 |
| [3] |
MOHAMMADI M. Optimum engineered infilled frames and the influence of openings[J]. Structures and Buildings, 2017, 170(5): 354-361. |
| [4] |
ONAT O, LOURENCO P B, KOÇAK A. Experimental and numerical analysis of RC structure with two leaf cavity wall subjected to shake table[J]. Structural Engineering & Mechanics, 2015, 55(5): 1037-1053. |
| [5] |
魏文晖, 徐沛韬, 高湛, 等. 框架-嵌入式墙体结构抗震性能试验研究与有限元分析[J]. 建筑结构学报, 2017, 38(5): 92-99. WEI Wenhui, XU Peitao, GAO Zhan, et al. Experimental and analytical study on seismic performance of frame-embedded walls[J]. Journal of Building Structures, 2017, 38(5): 92-99. |
| [6] |
郭宏超, 孙立建, 刘云贺, 等. 内填再生混凝土墙的柔性钢框架结构抗震性能试验研究[J]. 建筑结构学报, 2017, 38(7): 103-112, 128. GUO Hongchao, SUN Lijian, LIU Yunhe, et al. Experimental research on seismic behavior of flexible steel frame with infilling recycled concrete wall[J]. Journal of Building Structures, 2017, 38(7): 103-112, 128. |
| [7] |
陈晓, 王曙光, 刘伟庆. 柔性连接叠合填充墙板-框架结构抗震性能试验研究[J]. 建筑结构学报, 2014, 35(12): 37-43. CHEN Xiao, WANG Shuguang, LIU Weiqing, et al. Experimental study on seismic behaviors of composite filling wall-frame structures with flexible connection[J]. Journal of Building Structures, 2014, 35(12): 37-43. |
| [8] |
金晓飞, 高松召, 杨晓杰, 等. 内嵌墙板钢框架等效单斜撑简化模型[J]. 哈尔滨工业大学学报, 2013, 45(6): 16-21. JIN Xiaofei, GAO Songzhao, YANG Xiaojie, et al. Equivalent single strut simplified model for steel frames with embedded retaining wall[J]. Journal of Harbin Institute of Technology, 2013, 45(6): 16-21. DOI:10.11918/j.issn.0367-6234.2013.06.003 |
| [9] |
ASTERIS P G, CAVALERI L, TRAPANI F D, et al. A macro-modelling approach for the analysis of infilled frame structures considering the effects of openings and vertical loads[J]. Structure and Infrastructure Engineering, 2016, 12(5): 551-566. DOI:10.1080/15732479.2015.1030761 |
| [10] |
NASIRI E, LIU Y. Development of a detailed 3D FE model for analysis of the in-plane behaviour of masonry infilled concrete frames[J]. Engineering Structures, 2017, 143(5): 603-616. |
| [11] |
张建伟, 杨兴民, 曹万林, 等. 单排配筋剪力墙结构抗震性能及设计研究[J]. 世界地震工程, 2009(1): 77-81. ZHANG Jianwei, YANG Xingming, CAO Wanlin, et al. Seismic behavior and design method of RC shear wall structure with single row of steel bars[J]. Word Earthquake Engineering, 2009(1): 77-81. |
| [12] |
杨兴民, 曹万林, 张建伟, 等. 三层单排配筋剪力墙结构抗震性能试验研究[J]. 地震工程与工程振动, 2009, 29(2): 92-97. YANG Xingmin, CAO Wanlin, ZHANG Jianwei, et al. Experimental study on seismic performance of a three-layer shear wall structure with single row of steel bars[J]. Journal of Earthquake Engineering and Engineering Vibration, 2009, 29(2): 92-97. |
| [13] |
吴波, 李惠, 李玉华. 结构损伤分析的力学方法[J]. 地震工程与工程振动, 1997, 17(1): 14-21. WU Bo, LI Hui, LI Yuhua. The mechanic method for damage analysis of structures[J]. Journal of Earthquake Engineering and Engineering Vibration, 1997, 17(1): 14-21. |
 2018, Vol. 50
2018, Vol. 50


