2. 亚热带建筑科学国家重点实验室(华南理工大学), 广州 510641
2. State Key Laboratory of Subtropical Building Science (South China University of Technology), Guangzhou 510641, China
钢筋混凝土(RC)剪力墙为高层建筑结构重要的承重及抗侧力构件,在实际工程中,往往会在剪力墙端部布置翼缘,使得在荷载作用下墙体与翼缘产生相互作用[1],形成T形剪力墙等.
国内外学者对T形RC剪力墙开展了相关试验研究,Thomsen等[2]、Sittipunt等[3]、Palermo等[4]根据T形RC剪力墙试验结果发现带翼缘的RC剪力墙与矩形剪力墙的抗震性能与破坏形态存在较大差异;李青宁等[5-6]通过试验发现T形短肢剪力墙存在明显的剪力滞后现象;傅剑平等[7-8]通过试验发现构件抗弯承载能力是影响其剪切效应的决定性因素;曹万林等[9]通过试验研究对比T形带暗支撑短肢剪力墙与普通剪力墙的抗震性能水平差异;朱张峰等[10]通过试验研究对比了T形预制装配式剪力墙与现浇剪力墙的抗震性能;吕西林等[11-12]通过缩尺RC剪力墙试验发现较强的约束边缘会使其延性及耗能水平有所降低.上述研究主要集中在对T形剪力墙的抗震性能方面的探讨,少有对T形剪力墙不同破坏状态与变形值之间定量关系的深入研究.
为此,本文通过改变剪跨比、设计轴压比及暗柱纵筋配筋率设计了12个T形RC剪力墙试件进行低周往复试验,分析其破坏形态、滞回性能、耗能能力、变形能力等结果,建立构件不同性能状态下损伤程度与变形值之间的定量对应关系,同时结合收集的试验结果进行回归分析,建立T形RC剪力墙不同性能状态的变形指标限值.
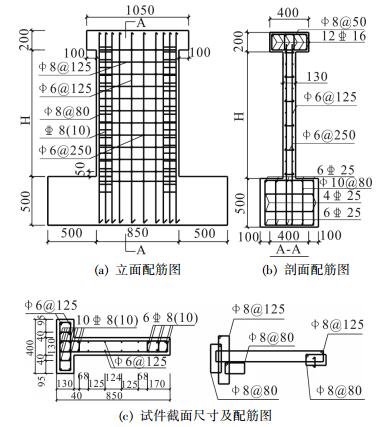
1 试验概况 1.1 试件设计与制作根据《建筑抗震设计规范》[13]和《混凝土结构设计规范》[14],设计了12个T形RC剪力墙试件,翼缘截面尺寸为400 mm×130 mm,腹板截面尺寸为720 mm×130 mm,墙体净高H分别为1 300 mm、1 700 mm、2 200 mm.试件设计了1.65、2.12、2.71三种剪跨比(λ),0.2、0.5两种设计轴压比(n)和1.55%、2.42%两种暗柱纵筋配筋率(ρ),共12种组合,分别为编号TW1~TW12的12个试件,基本参数见表 1,几何尺寸及配筋见图 1.试件所使用混凝土和钢筋材料实测性能见表 2、表 3.
| 表 1 试件基本参数 Table 1 Parameters of specimens |
|
图 1 试件几何尺寸及配筋图(mm) Figure 1 Geometry and reinforcement details of specimens(mm) |
| 表 2 混凝土实测力学性能 Table 2 Mechanical properties of concrete |
| 表 3 钢筋实测力学性能 Table 3 Mechanical properties of reinforcement bars |
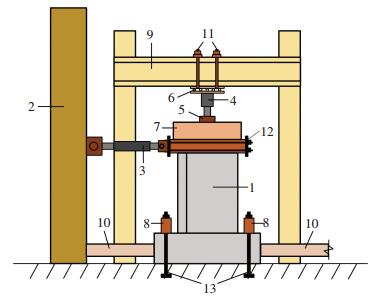
试验的加载装置见图 2.
|
1.试件2.反力墙3.MTS作动器4.液压千斤顶5.球铰6.滚轴7.刚性垫梁8.压梁9.反力架10.水平固定梁11.竖向千斤顶固定螺栓12.水平连接装置13.地锚螺栓 图 2 加载装置示意 Figure 2 Test setup |
试验首先施加轴压力并维持恒定,然后施加水平荷载进行低周往复试验,先使翼缘受压加载(正向加载),后使翼缘受拉加载(负向加载).水平荷载的施加采用荷载、位移混合控制的加载制度[15]:试件屈服前,采用力控制,每级递增20~40 kN加载,每级荷载循环一次;当试件最外层纵筋屈服或荷载-位移曲线显著偏离直线时,认为试件屈服,以正负向屈服位移平均值作为试件屈服位移Δy;试件屈服后,采用位移控制,以屈服位移Δy的倍数进行循环加载,每级位移加载循环三次,加载至试件破坏,直至试件丧失竖向承载力或者水平承载力下降至峰值承载力的50%左右.
2 结果及分析 2.1 破坏形态和破坏过程12个T形剪力墙试件的最终破坏形态见图 3.根据试验结果,试件的破坏形态主要分为弯曲破坏和弯剪破坏两种.

|
图 3 试件破坏形态 Figure 3 Failure patterns of specimens |
1) 弯曲破坏:试件屈服前,墙身裂缝以水平裂缝为主,且集中于底部塑性区.试件屈服后,在试件底部约0.5倍截面高度范围内出现塑性铰,墙身部分水平裂缝斜向延伸形成斜裂缝,但裂缝宽度较小;试件无翼缘端首先破坏.试件破坏时,全部纵筋及大部分水平筋、箍筋屈服;塑性区无翼缘端混凝土被压碎,暗柱纵筋被压曲或拉断,构件塑性区无翼缘端破坏严重,而翼缘端损伤轻微,仅出现裂缝.试件TW5~TW12发生弯曲破坏.
2) 弯剪破坏:试件屈服前,试件翼缘与腹板端部产生水平裂缝,随后有较多水平裂缝向腹板中心斜向延伸.试件屈服后,墙身产生大量交叉斜裂缝,裂缝宽度较大;与弯曲破坏相比,弯剪破坏试件剪切变形所占比例更高,斜裂缝的倾角更大,裂缝分布范围至试件全高;试件无翼缘端首先破坏,在竖向荷载作用下破坏加剧,试件承载力迅速下降.试件破坏时,墙体中部产生较大宽度的交叉斜裂缝,混凝土严重剥落;试件无翼缘端根部破坏严重,塑性区大块混凝土压碎、剥落,暗柱纵筋压曲、拉断,而翼缘端轻度损伤,有较大宽度裂缝产生.试件TW1~TW4发生弯剪破坏.
由试验结果可知,剪跨比对破坏形态的影响最大.随着剪跨比的减小,T形剪力墙的破坏形态由弯曲破坏转向弯剪破坏.
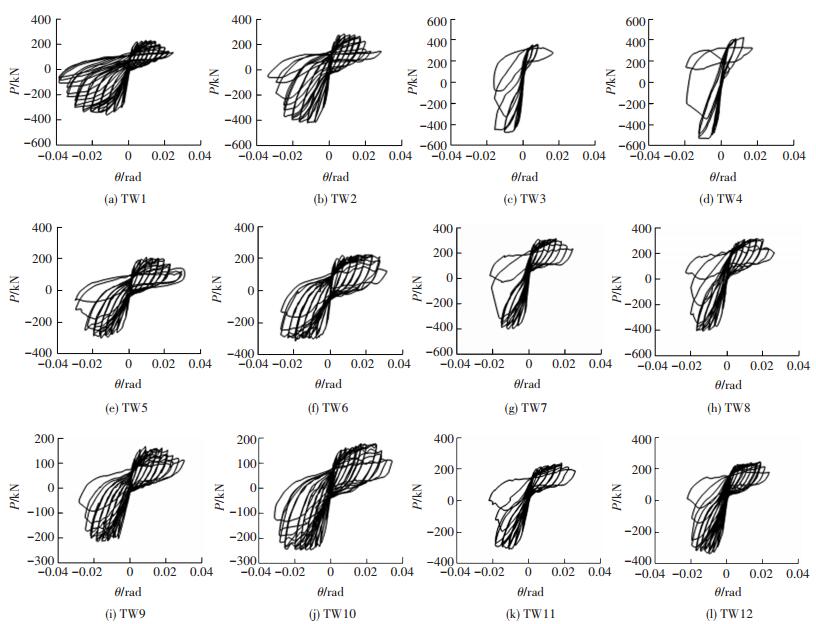
2.2 滞回曲线及骨架曲线各试件的顶部水平荷载P-位移角θ滞回曲线及骨架曲线分别见图 4、5.
|
图 4 试件顶部水平荷载P-位移角θ滞回曲线 Figure 4 P-θ hysteretic loops of specimens |

|
图 5 试件顶部水平荷载P-位移角θ骨架曲线 Figure 5 P-θ skeleton curves of specimens |
由图 4可知:1)由于设置翼缘,T形剪力墙不对称,试件滞回曲线的正、负向特征明显不同.正向加载时,翼缘受压,无翼缘端暗柱纵筋受拉,滞回曲线较为饱满,耗能能力较强;负向加载时,翼缘受拉,无翼缘端暗柱纵筋易于压曲,混凝土压碎,滞回环面积在试件承载力到达峰值后明显减小,耗能能力较弱;2)弯曲破坏试件(TW5~TW12)的滞回曲线较为饱满,在加载初期滞回环内凹呈“弓”形,后期发展为反“S”形,试件的变形及耗能能力较好;与弯曲破坏相比,弯剪破坏试件(TW1~TW4)剪切变形所占比例增大,剪切效应产生,捏缩效应增强,滞回曲线饱满程度降低,耗能能力减弱;3)随着剪跨比的增大,试件耗能能力增强;随着轴压比的增大,试件承载力显著提高,但捏缩效应增强,耗能能力减弱;随着暗柱纵筋配筋率的增大,试件滞回环特性变化不大,承载力有所提升.
由图 5可知,试件的骨架曲线正负向具有差异性.与正向加载相比,负向加载时,由于翼缘配置的竖向钢筋受拉,试件承载力明显大于正向,但试件承载力到达峰值后,无翼缘端暗柱纵筋易于压曲,混凝土过早压碎,负向迅速丧失承载力,延性降低,高轴压比时尤为明显.
对比不同参数下的骨架曲线,可以看出:1)增大暗柱纵筋配筋率,能提高试件的承载力,对弯剪破坏试件尤为明显;对弯曲破坏试件的变形能力影响不大,但会降低弯剪破坏试件的变形能力;2)增大轴压比,试件承载能力显著增大,但骨架曲线下降段变陡,变形能力变小,弯剪破坏试件尤为明显;3)增大剪跨比,试件骨架曲线的平台段变长,下降段变缓,变形能力变强.
3 变形指标限值 3.1 变形指标限值的划分采用变形指标限值定量评估T形RC剪力墙的抗震性能和变形能力.结合相关研究成果[16-17]及规范[13]对性能状态的划分标准,将T形RC剪力墙划分为6个性能状态:完好(G1)、轻微损坏(G2)、轻中等破坏(G3)、中等破坏(G4)、较严重破坏(G5)、严重破坏(G6),构件超过严重破坏状态为失效.采用以下两种方法确定构件不同性能状态的变形限值.
1) 方法一:基于骨架曲线的划分方法
根据试验骨架曲线,由Park[18]等效屈服点方法确定的位移角为“完好”状态的变形限值θ1;水平承载力下降20%对应的位移角为“较严重破坏”的变形限值θ5;“严重破坏”的变形限值θ6为构件丧失竖向承载力与水平承载力下降至峰值承载力的50%两者对应位移角的较小值;轻微损坏、轻中等破坏与中等破坏的变形限值θ2、θ3与θ4由θ1和θ5等分插值所得,见式(1)~(3)[19].基于骨架曲线的变形限值划分结果见图 6.

|
图 6 基于骨架曲线的变形限值划分方法 Figure 6 Definition of deformation index limits based on skeleton curve |
| $ {\theta _2} = {\theta _1} + 0.25\left( {{\theta _5}-{\theta _1}} \right), $ | (1) |
| $ {\theta _3} = {\theta _1} + 0.50\left( {{\theta _5}-{\theta _1}} \right), $ | (2) |
| $ {\theta _4} = {\theta _1} + 0.75\left( {{\theta _5}-{\theta _1}} \right). $ | (3) |
2) 方法二:现象特征点划分法
试验过程可归纳出的10个主要的试验现象:(1)开裂;(2)暗柱约束区受拉纵筋屈服;(3)墙面最大裂缝宽度达到1 mm;(4)墙面最大裂缝宽度达到2 mm;(5)混凝土保护层轻微剥落;(6)混凝土保护层严重剥落;(7)暗柱纵筋外露;(8)暗柱纵筋压曲;(9)暗柱纵筋拉断;(10)构件丧失轴向、侧向承载能力.根据主要试验现象出现的先后次序与损伤程度,上述(1)~(10)主要破坏现象可划分至不同性能状态中,见表 4,各性能状态的变形限值为对应试验现象位移角的最小值,分别为t1~t6.
| 表 4 剪力墙构件各性能状态对应损伤程度 Table 4 Damage extent of each performance state of reinforced concrete shear wall |
将方法一确定的变形指标限值θ1~θ6与方法二确定的变形指标限值t1~t6进行对比,统计结果见表 5.由对比结果可知,θ1/t1~θ6/t6的均值为0.96~1.18,表明根据骨架曲线划分的性能点位移角限值与试验现象位移角限值总体上十分接近;标准差为0.05~0.36,方差为0.002~0.13,表明比值离散性较小.
| 表 5 性能点与现象点变形值对比 Table 5 Comparison of deformation limits between performance points and phenomenon points |
综上所述,θ1~θ6与t1~t6吻合程度高,采用基于骨架曲线的划分方法能有效反映构件在不同性能状态下的损伤情况,得到的不同性能状态下的变形限值见表 6.
| 表 6 各试件不同性能状态的变形指标限值 Table 6 Deformation index limits for different performance states of specimens |
由3.1节基于骨架曲线确定性能状态的划分方法可知,“完好”(G1)状态、“较严重破坏”(G5)状态、“严重破坏”(G6)状态是确定试件变形限值与损伤情况的关键性能点.为进行T形RC剪力墙关键性能点变形限值的回归分析,从公开发表的文献收集了24个T形RC剪力墙试件的低周往复试验数据,收集结果见文献[17].从收集的24个试件及设计的12个试件共36个试件(翼缘与腹板的截面高度之比为0.56~1.33)中,提取控制参数剪跨比λ、设计轴压比n、暗柱纵筋配筋率ρ(%)及正负向3个关键性能点的变形限值(θ1、θ5、θ6),建立T形RC剪力墙正负向关键性能点变形限值的回归公式,其余的变形限值θ2、θ3与θ4可由θ1和θ5等分插值得到.
正向关键性能点变形限值回归公式:
θ1=0.003 9+0.000 8λ-0.006 0n+0.000 4ρ,
θ5=0.005 6+0.008 6λ-0.017 2n+0.003 7ρ,
θ6=0.009 1+0.011 1λ-0.036 1n+0.003 7ρ.
负向关键性能点变形限值回归公式为:
θ1=0.003 5+0.000 1λ-0.005 4n+0.001 2ρ,
θ5=0.014 4+0.001 6λ-0.007 0n+0.001 0ρ,
θ6=0.014 7+0.002 7λ-0.019 7n+0.002 5ρ.
T形RC剪力墙变形限值随着剪跨比、暗柱纵筋配筋率的增大呈增大趋势,随着设计轴压比的增大呈减小趋势.
4 结论1) T形RC剪力墙的破坏形态主要受剪跨比影响,随着剪跨比减小,破坏形态由弯曲破坏转向弯剪破坏.
2) 弯剪破坏剪力墙试件的变形和耗能能力低于弯曲破坏试件,但通过降低设计轴压比、降低截面抗弯承载力等措施可以适当提高弯剪破坏剪力墙的抗震变形和耗能能力.
3) 采用基于骨架曲线的划分方法能合理有效地反映T形RC剪力墙在不同性能状态下的损伤程度,由此可建立构件变形限值与损伤程度的对应关系.
4) 建立T形RC剪力墙试件关键性能点的变形指标限值的回归公式,其中变形指标限值随剪跨比、暗柱纵筋配筋率增大而增大,随设计轴压比增大而减小.
| [1] |
史庆轩, 王斌, 王朋, 等. 双轴加载下RC带翼缘剪力墙抗震性能对比分析[J]. 福州大学学报(自然科学版), 2013, 41(4): 712-716. SHI Qingxuan, WANG Bin, WANG Peng, et al. Comparison and analysis for seismic performance of RC shear wall with flanges under biaxial loading[J]. Journal of Fuzhou University (Natural Science Edition), 2013, 41(4): 712-716. DOI:10.7631/issn.1000-2243.2013.04.712 |
| [2] |
THOMSEN J H, WALLACE J W. Displacement-based design of slender reinforced concrete structural walls-experimental verification[J]. Journal of Structural Engineering, 2004, 130(4): 618-630. DOI:10.1061/(ASCE)0733-9445(2004)130:4(618) |
| [3] |
SITTIPUNT C, WOOD S L. Influence of web reinforcement on the cyclic response of structural walls[J]. ACI Structural Journal, 1995, 92(6): 745-756. |
| [4] |
PALERMO D, VECCHIO F J. Behaviour of three dimensional reinforced concrete shear wall[J]. Journal of the American Concrete Institute, 2002, 99(1): 181-189. |
| [5] |
李青宁, 李晓蕾, 闫艳伟, 等. 钢筋混凝土短肢剪力墙抗震性能试验研究[J]. 建筑结构学报, 2011, 32(4): 53-62. LI Qingning, LI Xiaolei, YAN Yanwei, et al. Experimental research on seismic performance of reinforced concrete short-leg shear wall[J]. Journal of Building Structures, 2011, 32(4): 53-62. |
| [6] |
李青宁, 李晓蕾, 雷伟宁. T形与L形短肢剪力墙破坏规律及刚度延性研究[J]. 建筑结构, 2010, 40(2): 37-39, 44. LI Qingning, LI Xiaolei, LEI Weining. Study on destruction law and stiffness ductility of T-shaped and L-shaped short shear wall[J]. Building Structure, 2010, 40(2): 37-39, 44. |
| [7] |
傅剑平, 吴雁江, 皮天祥, 等. 工字形截面延性剪力墙肢抗震抗剪性能试验[J]. 重庆大学学报(自然科学版), 2004, 27(12): 52-55, 67. FU Jianping, WU Yanjiang, PI Tianxiang, et al. Experimental research on seismic shear capacity of I-shape ductile reinforced concrete structural walls[J]. Journal of Chongqing University (Natural Science Edition), 2004, 27(12): 52-55, 67. |
| [8] |
傅剑平, 汪锦林, 白绍良. 工字形、T形钢筋混凝土剪力墙抗震抗剪试验[J]. 重庆建筑大学学报, 2008, 30(3): 22-26. FU Jianping, WANG Jinlin, BAI Shaoliang. The seismic shear capacity of I-shaped and T-shaped reinforced concrete structural walls[J]. Journal of Chongqing Jianzhu University, 2008, 30(3): 22-26. |
| [9] |
曹万林, 常卫华, 宋文勇, 等. 带暗支撑T形截面短肢剪力墙抗震性能试验研究[J]. 世界地震工程, 2005, 21(2): 25-30. CAO Wanlin, CHANG Weihua, SONG Wenyong, et al. Experimental research on seismic behavior of T-Shaped short pier shear wall with concealed bracings[J]. World Earthquake Engineering, 2005, 21(2): 25-30. |
| [10] |
朱张峰, 郭正兴. 装配式短肢剪力墙平面模型抗震性能试验[J]. 哈尔滨工业大学学报, 2012, 44(4): 94-99. ZHU Zhangfeng, GUO Zhengxing. Test research on seismic performance of plane model of new precast concrete short-limbed shear wall[J]. Journal of Harbin Institute of Technology, 2012, 44(4): 94-99. DOI:10.11918/j.issn.0367-6234.2012.04.019 |
| [11] |
龚治国, 吕西林, 姬守中. 不同边缘构件约束剪力墙抗震性能试验研究[J]. 结构工程师, 2006, 22(1): 56-61. GONG Zhiguo, LU Xilin, JI Shouzhong. Experimental study on seismic behavior of RC shear walls with different boundary restraints[J]. Structural Engineers, 2006, 22(1): 56-61. |
| [12] |
章红梅, 吕西林, 杨雪平, 等. 边缘构件配箍对钢筋混凝土剪力墙抗震性能的影响[J]. 结构工程师, 2008, 24(5): 100-104, 118. ZHANG Hongmei, LU Xilin, YANG Xueping, et al. Influence of boundary stirrup on seismic behavior of reinforced concrete shear walls[J]. Structural Engineers, 2008, 24(5): 100-104, 118. |
| [13] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [14] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [15] |
建筑抗震试验规程: JGJ/T 101—2015[S]. 北京: 中国建筑工业出版社, 2015. Specification for seismic test of buildings: JGJ/T 101—2015[S]. Beijing: China Architecture & Building Press, 2015. |
| [16] |
戚永乐. 基于材料应变的RC梁、柱及剪力墙构件抗震性能指标限值研究[D]. 广州: 华南理工大学, 2012. QI Yongle. Research on deformation limits of RC beams, columns and shear walls based on material strain[D]. Guangzhou: South China University of Technology, 2012. |
| [17] |
王骜亚. 基于材料应变的T形钢筋混凝土剪力墙变形性能指标研究[D]. 广州: 华南理工大学, 2015. WANG Aoya. Research on deformation limits of T-shaped RC shear wall based on material strain[D]. Guangzhou: South China University of Technology, 2015. |
| [18] |
PARK R. Evaluation of ductility of structures and structural assemblages from laboratory testing[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1989, 22(3): 155-166. |
| [19] |
孙典龙. 矩形截面RC剪力墙的抗震性能及其性能指标试验研究[D]. 广州: 华南理工大学, 2016. SUN Dianlong. Experimental research on the seismic performance and performance index limits of RC shear wall with rectangular section[D]. Guangzhou: South China University of Technology, 2016. |
 2018, Vol. 50
2018, Vol. 50



 8(1.55%)
8(1.55%)