2. 抗震工程技术四川省重点实验室(西南交通大学),成都 610031;
3. 中铁第六勘察设计院集团有限公司,天津 300308
2. Key Laboratory of Seismic Engineering of Sichuan Province (Southwest Jiaotong University), Chengdu 610031, China;
3. China Railway Liuyuan Group Co., Ltd., Tianjin 300308, China
近年来,中国发生的汶川地震和芦山地震造成了灾区大量建筑的破坏和倒塌[1-2].这使得地震易损性分析越来越受到重视.对建筑物进行易损性分析,震前可以预测震害情况,帮助设计人员提高结构的抗震能力;震后可以进行损失评估,为灾害估计和救灾重建提供依据.国内外学者对此问题进行了大量研究.Ozaki等[3]对基于线性和非线性响应的传统方法进行了改进,并将改进后的方法用于反应堆厂房的地震易损性分析; 尹之潜等[4]为与新的地震动参数区划图接轨,克服以烈度为依据的震害预测方法的缺陷,提出了以地震加速度谱值为输入参数的建筑物易损性分析; Schotanus等[5]对钢筋混凝土框架结构时变系统可靠度的地震易损性进行了分析; 吕大刚等[6-7]对钢筋混凝土结构进行了整体抗震能力分析和地震易损性分析,得到了该结构的概率地震需求模型和易损性曲线; Buratti等[8]考虑结构参数和地震激励的不确定性,对其地震易损性进行了评估; 刘晶波等[9]、吴巧云等[10]提出了基于结构极限破坏状态确定结构抗震性能水平的方法,并对结构进行基于性能的地震易损性分析,判断其所处的地震破坏状态.目前,对现浇钢筋混凝土框架结构(下文简称:现浇结构)地震易损性的研究较多,而鲜有对预应力装配式框架结构(下文简称:装配式结构)地震易损性进行分析.
装配式结构因具有施工工期短、施工质量易于控制、对环境影响小等优点,正得到大力推广.近年来,装配式结构的研究也广泛开展起来.Priestley等[11]对两个后张预应力装配式梁柱节点进行了低周反复加载试验,分析了装配式梁柱节点的耗能表现; 郭彤等[12]提出腹板摩擦式预应力装配式节点构造,研究了节点的力学行为和耗能能力; Deng等[13-14]通过实验研究了带预应力钢绞线的装配式自复位梁柱节点的抗震性能,实验结果表明该节点具有良好的耗能能力和承载力.目前,装配式结构的研究多集中在梁柱节点方面,而针对整体结构性能的研究还较少.
针对装配式结构地震易损性研究的不足,本文从无黏结预应力装配式节点入手,采用增量动力分析方法(incremental dynamic analysis,简称IDA)对一栋六层装配式结构进行易损性分析,并与现浇结构进行对比,预测装配式结构在不同等级的地震作用下发生破坏的概率,为装配式结构的抗震性能评估提供科学依据.
1 结构模型及地震动选取 1.1 梁柱节点模型的建立基于OpenSEES分析软件,本文采用零长度单元释放装配式结构的梁端刚度以模拟节点的半刚性,预应力钢绞线采用桁架单元,装配式结构和现浇结构的梁、柱均采用非线性梁柱单元[15].节点模型的建立如图 1所示.该模型共包含6个节点和5个单元,其中2号节点和4号节点之间是零长单元,其他单元为普通梁单元.零长单元用于模拟节点区的界面抗剪行为,释放2、4节点之间的转动自由度,约束其平动自由度.普通梁柱单元的混凝土和钢筋的本构模型分别采用修正后的Kent-Park本构模型和Pinto本构模型.
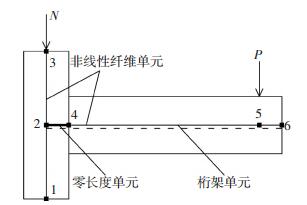
|
图 1 装配式结构节点模型 Figure 1 Beam-column joint model of assembled RC frame |
为验证本文建模方法的有效性,选取文献[16]中的3个后张无黏结预应力装配式混凝土节点试验,采用上述建模方式对这3个节点试件进行模拟分析,计算结果与试验结果的对比如图 2所示.由图 2可见,模拟结果与试验结果在峰值荷载,卸载刚度等力学特性上存在一定的误差.这些误差主要来源于纤维模型与实际结构的误差.纤维模型难以模拟出预制梁柱之间的接触效应,故滞回曲线的捏拢效应会略低于试验结果.但二者的滞回曲线特征基本吻合,说明本文采用的建模方法有效,可用于装配式结构的易损性分析.

|
图 2 梁柱节点滞回曲线比较 Figure 2 Comparison of hysteresis curves of beam-column connection |
根据中国建筑结构设计规范[17-20],设计了一栋六层无黏结预应力装配式结构,其平面、Ⅰ-Ⅰ剖面如图 3所示.该结构位于西南地区某省会城市,地震分组为第三组,Ⅱ类场地、抗震设防烈度7度(0.1g).屋面恒载为5.0 kN/m2,活载为0.5 kN/m2;楼面恒载为4.0 kN/m2,活载为2.0 kN/m2;梁间线荷载为9.6 kN/m,基本风压为0.35 kN/m2,基本雪压为0.15 kN/m2,该框架结构满足相应规程要求的适用范围[19-20].
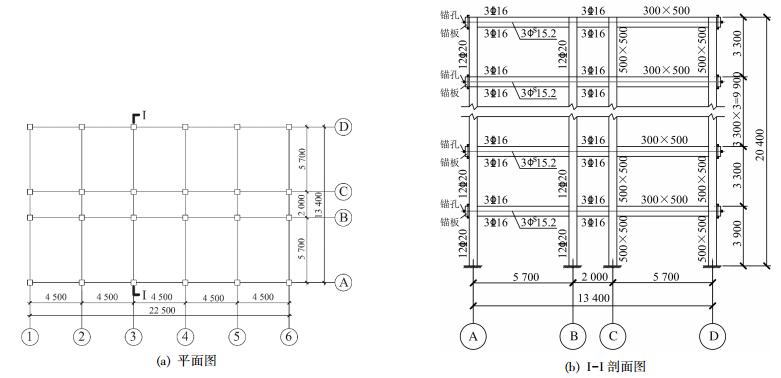
|
图 3 装配式结构(mm) Figure 3 The fabricated RC frame structure(mm) |
现浇结构的结构平面布置,梁柱截面的尺寸、配筋率均保持与装配式结构相同.两种结构均选取Ⅰ-Ⅰ剖面作为分析对象,梁、柱配筋如图 4所示.采用OpenSEES软件对结构进行非线性分析.框架梁柱按照上述建模方式在OpenSEES中建立模型,预应力筋采用桁架单元.

|
图 4 梁、柱配筋 Figure 4 Reinforcements of beams and columns |
梁、柱采用C40混凝土,轴心抗压强度为26.8 MPa,抗压应变为1.589×10-3;轴心抗拉强度为2.39 MPa,抗拉应变为1.044×10-4,弹性模量为3.25×104 MPa.无黏结预应力筋为1×7的ΦS 15.2钢绞线,预应力度为0.55,初始应力为1 023 kN,沿梁截面中性轴对称布置,钢筋的力学性能参数见表 1, 装配式结构的节点见图 5.
| 表 1 钢筋的力学性能参数 Table 1 Parameters of reinforcement mechanics performance |
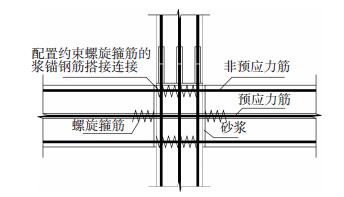
|
图 5 装配式结构节点示意 Figure 5 Diagram of fabricated frame structure node |
Ⅱ类场地类似于美国地震勘测中心(USGS)的S2类场地[21],采用美国ATC-63(2008)报告[22]中建议的选取原则.在美国太平洋地震研究中心(PEER)的强震动记录数据库中,选取了16条外国地震动记录和2条中国地震动记录,其反应谱和设计反应谱如图 6所示,选取的18条地震记录反应谱平均值与中国设计反应谱基本吻合.
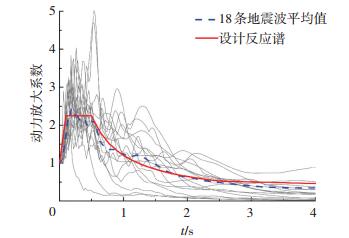
|
图 6 地震动反应谱 Figure 6 Response spectrums |
根据Vamvatsikos[23]建议,选取Sa(T1, 5%)作为地震动强度指标.
2 地震易损性分析 2.1 结构性态点的定义为了分析结构在地震作用下的性能,需要在IDA曲线上确定结构各种性能的状态.根据美国FEMA和中国《建筑抗震设计规范》的建议,本文选取4个典型性态点评估结构抗震能力:正常使用(简称NO),立即使用(简称IO),生命安全(简称LS)和防止倒塌(简称CP).
图 7为装配式结构在地震作用下的IDA曲线.对于NO、IO和LS三个性态点,均采用最大层间位移角θmax评定.由于地震作用较大时,结构出现大变形,装配式结构中预应力筋有可能屈服,导致结构的整体刚度下降,梁柱节点的残余变形过大.故本文CP性态点的判定标准为:IDA曲线斜率达到其初始斜率的20%或者最大预应力筋内力屈服,二者满足其一即认为达到CP性态点.
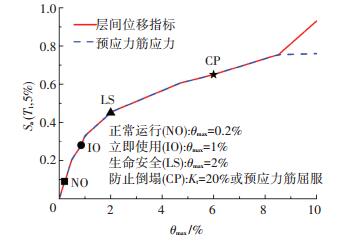
|
图 7 不同损伤指标的IDA曲线 Figure 7 IDA curve under different damage index |
对六层无黏结预应力装配式结构和现浇结构进行IDA分析.在OpenSEES中对两种结构模型进行弹塑性时程分析,根据2.1节提出的判定标准得到两种结构在18条地震动作用下的IDA曲线,见图 8.
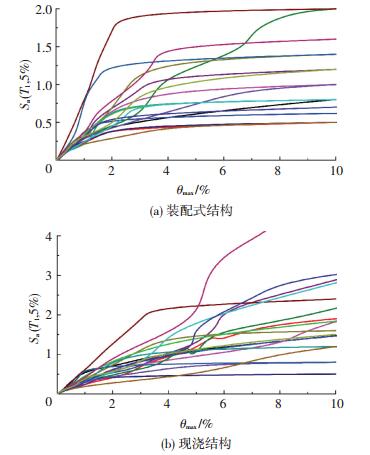
|
图 8 地震作用下的IDA曲线 Figure 8 IDA curves under earthquake |
由图 8可知,IDA曲线的特性与地震动的选取直接相关,由于地震动的不确定性,同一结构在不同地震动激励下的IDA的曲线有较强的离散性,故采用概率统计法对结构的IDA曲线进行分析.
假设IDA曲线服从正态分布,在某一结构损伤指标(Damage Measure,简称DM)下,得到不同地震动强度指标IM的均值和对数标准差,如图 9所示.当最大层间位移角超过3%时,现浇结构的地震动强度超过了装配式结构.

|
图 9 两种结构的IM均值和标准差 Figure 9 The average value and standard deviation of IM of two frame structures |
表 2统计了两种结构在NO、IO、LS和CP性态点处的最大层间位移角θmax和地震动强度Sa(T1, 5%).根据图 9和表 2可看出,在结构达到LS性态点之前,两种结构的地震动强度非常接近;当结构超过LS性能点时,现浇结构的地震动强度逐渐大于装配式结构的地震动强度;当结构达到CP性态点时,现浇结构对应的地震动强度超过了装配式结构.
| 表 2 两种结构性态点 Table 2 Performance points of two frame structures |
在CP性态点处,装配式结构的最大层间位移角(5%)和地震动强度指标(1.075g)均小于现浇结构的最大层间位移角(9.4%)和地震动强度指标(1.183g).需要说明的是,装配式结构中的预应力筋并未屈服,CP性态点为IDA曲线斜率达到其初始斜率20%的点.
装配式结构在CP性态点处的地震动强度指标低于现浇结构,主要原因有两个:1)在装配式结构的梁柱节点中,预应力筋未屈服,滞回曲线会呈现出明显的捏拢特性,表明其不能在地震中充分发挥其耗能能力.此外,梁柱分离后,预应力装配式节点的刚度显著下降,进一步增大得了结构的位移响应[13]; 2)对于现浇结构,框架梁中全部纵筋参与耗能,滞回曲线饱满,结构在地震下的等效阻尼比较大.当两个结构极限承载力相近时,现浇结构的耗能和屈服后刚度显著高于装配式结构,有利于控制结构的大震下的响应.综上所述,在罕遇地震作用下,柱截面尺寸和配筋相同、梁截面尺寸和受弯承载力相同时,在CP性态点处,装配式结构的最大层间位移角和地震动强度指标均小于现浇结构.
2.3 结构易损性曲线本文假定结构需求参数均值

|
图 10 两种结构的地震概率需求模型 Figure 10 Probabilistic seismic demand model of two structures |
| $ \hat D = \alpha {\left( {{S_{\text{a}}}\left( {{T_1}, 5\% } \right)} \right)^\beta }, $ | (1) |
| $ \ln \left( {{\theta _{\max-{\text{zp}}}}} \right) = 0.842\ln \left( {{S_a}\left( {{T_1}, 5\% } \right)} \right)-3.649, $ | (2) |
| $ \ln \left( {{\theta _{\max-{\text{xj}}}}} \right) = 1.609\ln \left( {{S_a}\left( {{T_1}, 5\% } \right)} \right)-3.409. $ | (3) |
设结构地震需求参数D与地震能力参数C均服从对数正态分布[24],结构特定阶段失效概率Pf计算公式为
| $ {P_{\text{f}}} = \varphi \left[{\frac{{\ln \hat D-\ln \hat C}}{{\sqrt {\beta _{\text{c}}^2 + \beta _{\text{d}}^2} }}} \right]. $ | (4) |
式中:
以地震动强度指标Sa(T1, 5%)为横坐标,地震动作用下结构超越极限状态的概率为纵坐标,绘制装配式结构和现浇结构的地震易损性曲线,如图 11所示.

|
图 11 装配式结构与现浇结构易损性曲线对比 Figure 11 Comparison of fragility curves of two structures |
在地震动强度较小,结构达到NO性态点和IO性态点时,两种结构的易损性曲线几乎重合.结构达到LS性态点时,在地震动强度指标Sa(T1, 5%)≤0.5g时,两种结构的易损性曲线几乎重合.在地震动强度指标Sa(T1, 5%)≥0.5g时,在相同地震动强度指标下,现浇结构的超越概率稍大于装配式结构,当Sa(T1, 5%)=1.0g时,装配式结构和现浇结构达到LS性态点的概率分别为78.9%、90.6%.这是由于装配式结构进入弹塑性阶段后,梁端约束作用减弱,节点产生一定的转动,结构整体侧向刚度进一步减小,使得构件在地震作用下的内力减小,相应的地震反应均值小于刚性连接的现浇结构.
结构达到CP性态点时,两种结构的易损性曲线差异较大,当Sa(T1, 5%)=2.0g时,装配式结构和现浇结构达到CP性态点的概率分别为74.6%、23.1%.主要原因有两个:1)装配式结构的节点采用预应力筋拼装,结构的整体性和初始刚度弱于现浇结构; 2)进行IDA分析时,装配式结构的IDA曲线刚度下降幅值大于现浇结构.
综上所述,在多遇地震作用下,地震动强度较小时,装配式框架结构和现浇框架结构的抗倒塌能力接近,随着地震动强度的增大,在CP性态点处,预应力绞线无法提供充足的耗能能力,同时分离式预应力结构的消压后刚度较小,装配式框架结构的抗倒塌能力比现浇框架结构弱.
3 结论1) 当二者柱截面尺寸和配筋相同、梁截面尺寸和受弯承载力相同时,在水平地震作用下,预应力筋在整个过程中基本保持弹性,使得装配式节点的滞回曲线呈现出明显的捏拢特性,其地震能量耗散较现浇结构少,故在防止倒塌性态点(CP)处,装配式结构的最大层间位移角和地震动强度指标均小于现浇结构.
2) 在水平地震作用下,地震动强度较小时,装配式框架结构和现浇框架结构的抗倒塌能力接近,但随着地震动强度的增大,由于装配式结构的节点采用预应力筋拼装,进入弹塑性阶段后,结构整体侧向刚度进一步减小,因此在防止倒塌性态点(CP)处,装配式框架结构的抗倒塌能力比现浇框架结构弱.建议在装配式框架结构中增设阻尼器,以提高其强震下的抗倒塌能力.
| [1] |
清华大学土木结构组, 西南交通大学土木结构组, 北京交通大学土木结构组. 汶川地震建筑震害分析[J]. 建筑结构学报, 2008, 29(4): 1-9. Civil and structural groups of Tsinghua University, Southwest Jiaotong University, Beijing Jiaotong University. Analysis on building seismic damage in Wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(4): 1-9. DOI:10.3321/j.issn:1000-6869.2008.04.001 |
| [2] |
蔡晓光, 孙有为, 郭晓云. 芦山地震建筑震害统计分析[J]. 自然灾害学报, 2015, 24(6): 112-119. CAI Xiaoguang, SUN Youwei, GUO Xiaoyun. Statistical analysis of building damage in Ms 7.0 Lushan earthquake[J]. Journal of Natural Disasters, 2015, 24(6): 112-119. |
| [3] |
OZAKI M, OKAZAKI A, TOMOMOTO K, et al. Improved response factor methods for seismic fragility of reactor building[J]. Nuclear Engineering and Design, 1988, 185(2): 277-291. |
| [4] |
尹之潜, 赵直, 杨淑文. 建筑物易损性和地震损失与地震加速度谱值的关系(上)[J]. 地震工程与工程震动, 2003, 23(4): 195-200. YIN Zhiqian, ZHAO Zhi, YANG Shuwen. Relation between vulnerability of buildings and earthquake acceleration spectra(1)[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(4): 195-200. DOI:10.3969/j.issn.1000-1301.2003.04.033 |
| [5] |
SCHOTANUS M I J, FRANCHIN P, LUPOI A, et al. Seismic fragility analysis of 3D structures[J]. Structural Safety, 2004, 26(4): 421-441. DOI:10.1016/j.strusafe.2004.03.001 |
| [6] |
吕大刚, 于晓辉, 王光远. 基于MVFOSM有限元可靠度方法的结构整体概率抗震能力分析[J]. 世界地震工程, 2008, 24(2): 1-8. LV Dagang, YU Xiaohui, WANG Guangyuan. Global probabilistic seismic capacity analysis of structures based on MVFOSM finite element reliability method[J]. World Earthquake Engineering, 2008, 24(2): 1-8. |
| [7] |
吕大刚, 于晓辉, 潘峰, 等. 基于改进云图法的结构概率地震需求分析[J]. 世界地震工程, 2010, 26(1): 7-15. LV Dagang, YU Xiaohui, PAN Feng, et al. Probabilistic seismic demand analysis of structures based on an improved cloud method[J]. World Earthquake Engineering, 2010, 26(1): 7-15. |
| [8] |
BURATTI N, FERRACUTI B, SAVOIA M. Response Surface with random factors for seismic fragility of reinforced concrete frames[J]. Structural Safety, 2010, 32(1): 42-51. DOI:10.1016/j.strusafe.2009.06.003 |
| [9] |
刘晶波, 刘阳冰, 闫秋实, 等. 基于性能的方钢管混凝土框架结构地震易损性分析[J]. 土木工程学报, 2010, 43(2): 39-47. LIU Jingbo, LIU Yangbing, YAN Qiushi, et al. Performance-based seismic fragility analysis of CFST frame structures[J]. China Civil Engineering Journal, 2010, 43(2): 39-47. |
| [10] |
吴巧云, 朱宏平, 樊剑. 基于性能的钢筋混凝土框架结构地震易损性分析[J]. 工程力学, 2012, 29(9): 117-124. WU Qiaoyun, ZHU Hongping, FAN Jian. Performance-based seismic fragility analysis of RC frame structures[J]. Engineering Mechanics, 2012, 29(9): 117-124. |
| [11] |
PRIESTLEY M J N, MACRAE G A. Seismic tests of precast beam-to-column joint subassemblages with unbonded tendons[J]. PCI Journal, 1996, 41(1): 64-81. DOI:10.15554/pcij |
| [12] |
郭彤, 宋良龙, 张国栋, 等. 腹板摩擦式自定心预应力混凝土框架梁柱节点的试验研究[J]. 土木工程学报, 2012, 45(6): 23-32. GUO Tong, SONG Lianglong, ZHANG Guodong, et al. Experimental study on beam-column connections of self-centering prestressed concrete frame with web friction devices[J]. China Civil Engineering Journal, 2012, 45(6): 23-32. |
| [13] |
DENG K, PENG P, LAM A, et al. Test and simulation of full-scale self-centering beam-to-column connection[J]. Earthquake Engineering & Engineering Vibration, 2013, 12(4): 599-607. |
| [14] |
DENG K, PAN P, WU S. Experimental study on a self-centering coupling beam eliminating the beam elongation effect[J]. Structural Design of Tall & Special Buildings, 2016, 25(6): 265-277. |
| [15] |
陈学伟, 林哲. 结构弹塑性分析程序OpenSees原理与实例[M]. 北京: 中国建筑工业出版社, 2014: 166-171. CHEN Xuewei, LIN Zhe. Structural nonlinear analysis program OpenSees theory and tutorial[M]. Beijing: China Architecture & Building Press, 2014: 166-171. |
| [16] |
王东雁. 无粘结预应力装配混凝土节点抗震及震损加固性能研究[D]. 北京: 北京工业大学, 2008: 35-54. WANG Dongyan. Research of seismic performance and reinforcement performance of precast prestressed concrete connections with unbonded post-tensioned tendons[D]. Beijing: Beijing University of Technology, 2008: 35-54. |
| [17] |
建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [18] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [19] |
预应力混凝土结构抗震设计规程: JGJ 140—2004[S]. 北京: 中国建筑工业出版社, 2004. Specification for seismic design of prestressed concrete structures: JGJ 140—2004[S]. Beijing: China Architecture & Building Press, 2004. |
| [20] |
无粘结预应力混凝土结构技术规程: JGJ 92—2016[S]. 北京: 中国建筑工业出版社, 2016. Technical specification for concrete structures prestressed with unbonded tendons: JGJ 92—2016[S]. Beijing: China Architecture & Building Press, 2016. |
| [21] |
白久林, 欧进萍. 基于IDA方法的钢筋混凝土结构失效模式优化[J]. 工程力学, 2011, 28(SⅡ): 198-203. BAI Jiulin, OU Jinping. Optimization of failure modes for reinforced concrete buildings based on ida method[J]. Engineering Mechanics, 2011, 28(SⅡ): 198-203. |
| [22] |
ATC-63. Quantification of building seismic performance factors[R]. Redwood City, USA: Applied Technology Council, 2008.
|
| [23] |
VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis[J]. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491-514. DOI:10.1002/(ISSN)1096-9845 |
| [24] |
SUCUOGLU H, YUCEMEN S, GEZER A, et al. Statistical evaluation of the damage potential of earthquake ground motions[J]. Structural Safety, 1999, 20(4): 357-378. |
| [25] |
HAZUS99 User's manual[S]. Washington D C: Federal Emergency Management Agency, 1999.
|
 2018, Vol. 50
2018, Vol. 50


