东部沿海地区多分布海相湖相软土层,地下水位高,土层含水量大,浅层土体渗透系数k总体分布在10-5~10-7 cm/s数量级,属于低渗透性土体(k < 10-5 cm/s).在基坑开挖工程中如何排除潜水层地下水是一大技术难题.宁波地铁一号线樱花公园车站场地分布较厚的低渗透性淤泥、淤泥质黏土及黏土层,采用普通真空井降水,出水量极小,降水效果差.为解决这一问题,笔者所在课题组与中铁上海工程局合作研制高真空双管疏干井降水技术,经过现场试验验证,效果良好[1].真空降水技术[2]在中国地基处理及深基坑开挖工程中已经得到大量应用,但是在工程实践中,普通真空降水设备由于施工工艺的限制,密封性通常达不到要求,真空度通常仅维持在0.02~0.04 MPa,在低渗透性土层中降水效果不佳.高真空双管疏干井降水技术解决了管井密封性问题,真空度可维持在较高水平(0.07~0.09 MPa),除宁波外,亦在其他软黏土地区的工程实践中得到应用,但关于低渗透性土层高真空降水的理论研究还处于相对初级的阶段.
杨海旭等[3]通过对松花江漫滩区域实施真空井点联合加固软土地基的试验,验证了真空预压加快软土固结的有效性;周念清等[4]通过建立地下水渗流数值模型,并且借助抽水试验反求水文地质参数,结合场地边界条件和初始条件,使用三维有限差分法模拟基坑降水,同时计算了地面沉降;黄峰[5]对于非饱和粉土中的真空渗流场进行研究,通过现场实验得到包括真空度在内的多项指标的变化规律,对非饱和土,提出把进气值作为真空降水影响极限的标准,通过理论分析建立饱和土真空渗流场模型及真空降水的沉降模型;贾向新等[6]建立三维地下水流数值模型,将数值模拟预测数据与试验数据进行对比,提出真空井点周围存在真空及重力场耦合区、耦合场与重力场过渡区和重力场区3个区的概念,得出不同负压在不同井点深度条件下对地下水渗流场的影响规律;Li等[7]对水平方向的真空降水作用进行研究,并描述土层中的真空度变化规律;Huang等[8]通过室内模型实验,结合注气和真空方法,研究砂土中孔隙水在高压力梯度下的排出情况及土体沉降,研究发现增加注气可使排水量增加,土体沉降量减小.
上述有关真空降水的研究成果为本文的研究提供基础理论与出发点,但是前述真空管井降水的研究多集中在砂土、粉砂土等渗透系数相对较高的土层,针对低渗透性土层中高真空井降水规律的研究较少.为进一步从理论上研究低渗透性土层中真空度的传递规律及影响降水效率的因素,本文依托宁波地铁一号线樱花公园站基坑降水工程,采用数值模拟方法对高真空疏干井降水过程进行研究,总结降水时间、真空度、管井长度、井间距对真空度的传递规律及降水效率的影响.
1 工程背景 1.1 工程水文地质概况宁波地铁一号线樱花公园站场地地势较为平坦,地面标高平均约为2.5 m,属中心城区,拟建场地地处宁波平原中东部,地貌类型属海相沉积平原,土层分布及各自的物理力学参数见表 1.场地沿线地表水丰富,场区地下水由浅部土层中的潜水及深部粉(砂)性土层中的承压水组成,潜水主要赋存于浅部黏土、粉质黏土中.地下水位随降雨及潮汛影响而略有变化,根据勘察资料,变化幅度不大,一般在地表以下0.5~1.0 m.
| 表 1 土层计算参数 Table 1 Parameters of the soil |
从表 1得知,场地上部潜水区分布有很厚的淤泥及淤泥质黏土层,土层的渗透系数很小,基本在10-7 cm/s数量级,这给施工降水造成困难.
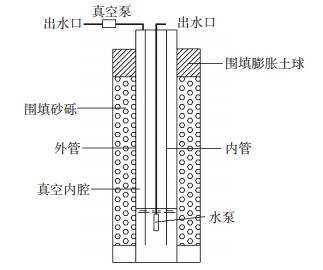
1.2 高真空双管结构简介实践表明,常规真空管井密封性较差,导致在低渗透性土层中出水量小,有时甚至难以出水,降水效率低下.高真空双管疏干井结构采用双管形成内外腔,内外管在顶部通过法兰盘焊接在一起,法兰盘上留有真空抽水孔与真空泵连接.内腔底部采用水封措施保持两管间的高真空,解决了普通管井真空度难以维持的问题.
井身结构见图 1.内、外管采用钢管材料,外管直径273 mm,由封闭段(工程上俗称“死管”)和滤水管段组成.上段(4 m)为封闭段,下段为滤管段,滤管段开孔,外包纱网或土工织物;内管直径为150~200 mm,为封闭段,其长度取决于降水深度,内管底部为开放式,为保证内、外管之间的真空状态,内管底部应永远处于井内水位以下至少1 m;内管中安装抽水泵,并使其吸水口高于内管的底部.
|
图 1 高真空双管结构示意 Figure 1 High vacuum double pipe structure schematic diagram |
高真空双管疏干井结构的工作原理是内外管间的高真空度通过滤管传递到土层后形成一定范围的真空负压区,地下水受到土层中真空负压区的影响,水力梯度增大,加速其向管井内的渗流速度,降水效率因此得到提升.抽水过程中,当地下水位与井管管口高差不超过最大真空高度,可用真空泵直接抽水,而当井管周围地下水位下降较大,与井口高程差超过最大真空高度时,需开启内管潜水泵抽水.
1.3 现场试验本次樱花公园地铁站的现场试验中[1, 9],分别进行16 m深的普通管井与高真空管井降水试验,并记录相应的出水量.从试验结果来看,普通降水井的平均出水量为0.009 8 m3/h,而高真空降水井平均出水量可达0.151 m3/h, 后者是前者的10倍以上.现场试验表明,高真空双管疏干井在低渗透性土层中具有较强的实用性,试验过程中,管井内真空度可保持在0.07 ~0.09 MPa,与普通真空降水井比较,在真空度维持及涌水量方面有较大的优势.
2 FLAC3D高真空井数值模拟 2.1 数值模拟范围与约束条件三维数值模拟中,首先合理划定计算用模型的区域范围,以此消除包括地下水边界效应在内的各种边界因素对于计算结果的影响.根据现场试验结果[1, 9],本工况下高真空井的影响半径不超过10 m,前期试算建立了不同大小的降水井模型,计算结果发现低渗透性土层真空井影响半径小于10 m,与试验结果一致.所以本次建立的模型横截面选取20 m边长的正方形,z轴方向尺寸取49.50 m,超过最大井深的1.5倍,以便消除底部边界的影响.模型尺寸为20 m×20 m×49.50 m, 降水井的直径为273 mm.以降水井为中心,井周2 m范围内网格加密,2 m范围以外,网格尺寸沿径向逐渐加大.模型示意图及网格划分见图 2、3.

|
图 2 模型土层分布 Figure 2 Schematic of soil distribution |

|
图 3 模型网格剖分 Figure 3 The subdivision of model nets |
模型土层参数采用宁波地铁樱花公园站现场土层,总共有14层,土层计算参数见表 1.
模型底部为固定位移边界,四周为水平向位移固定边界.模型计算时,首先进行初始地应力平衡,初始位移进行归零处理.当渗透系数较低时,水流汇集速度很慢,因此模型四周与底部都设置不透水边界条件.管井壁上部4 m的封闭管段设置为不透水边界,滤水段为透水边界.简化起见,地下水位设在地表,以利于观察土体中浸润线的变化.
土体应力应变关系使用摩尔库伦本构模型,该模型能反映岩土类材料的抗压和抗拉强度的不对称性及对于静水压力的敏感性,模型参数较少且其计算结果在变形不大时接近实际情况,FLAC3D流固耦合计算中常采用此本构模型[10].通过定义比奥模量考虑土粒可压缩性.管井内真空负压的模拟,是通过对井壁滤水段赋以包括上部恒定不变的一段负压边界以及下部梯度变化的一段负压边界[11]来实现.梯度变化的负压边界参考真空度在非饱和土中逐渐衰减的规律,Indraratna等[12]将真空负压绝对值视为随深度和水平距离呈线性减小,其利用此规律来模拟负压的作用.井内水位面处孔压设置为零.
程序运算开启渗流模式后,定义qflac函数来统计每秒井体整个内壁的节点流量总和,此值与相应时间积分可得不同时间下真空管井的出水总量.本文流固耦合计算中考虑到应力场对渗流场的影响,使用“修正的变单元渗透系数法”[13],用fish函数根据变化的应力值代入渗流支配方程计算变化后的渗透系数,然后用fish函数重赋渗透系数,实现渗透系数随孔压而变化的模拟.
2.2 模型合理性验证根据1.3节现场试验中管井尺寸,建立16 m的普通管井模型和真空井模型.模拟结果得到普通井(真空度为0)的出水量为0.011 5 m3/h,与现场试验得到的0.009 8 m3/h误差在20%之内.真空度最大值为0.08 MPa的真空管井模型计算得到的出水量为0.117 m3/h,与现场试验结果0.102 m3/h误差在20%之内.此处数值模拟结果偏大是由于现场试验管井在成井时有涂抹效应,导致井壁周围的土体渗透系数降低,出水量因此减少.普通井与高真空井的出水量模拟值与现场测试值均在同一数量级,因此使用此模型模拟高真空降水过程,以分析相关降水规律是可行的[14].
2.3 模拟结果与分析本文首先对单井的抽水过程进行模拟,研究不同真空度、不同井深、不同抽水时长下高真空井的降水效率和孔隙水压力的变化规律.
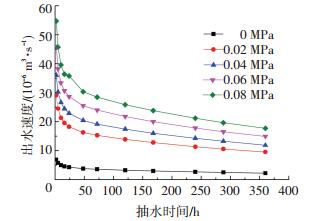
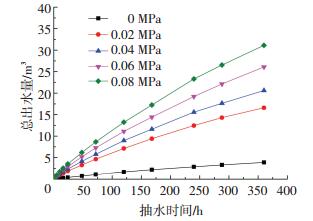
2.3.1 单井出水量变化规律图 4给出不同真空度下管井出水速度随时间的变化曲线,图 5给出不同真空度下管井出水总量随时间的变化曲线,图 6给出管井内真空度为0.08 MPa时单井日平均出水量随井深的变化曲线.
|
图 4 不同真空度下出水速度随时间变化曲线 Figure 4 The change of discharge with time under different vacuum |
|
图 5 不同真空度下出水总量随时间变化曲线 Figure 5 The change of total amount of discharge with time under different vacuum |

|
图 6 日平均出水量随井深的变化曲线 Figure 6 The change of discharge per day with well depth |
1) 由图 4可知,不同真空度下的所有工况在开始抽水时管井出水速度整体较大,在30~60 cm3/s,此时管井周围土体含水量较大.随着抽水时间增加,出水速度逐渐下降,连续抽水30 d后,出水速度稳定在5 ~15 cm3/s.出水速度随时间减小,是由于井周土体含水量随抽水的进行而减少,土体变得更加密实,渗透系数变得更小,则地下水汇集会越加困难.
2) 由图 5可知,随着管井内真空度增大,管井出水量递增.无真空普通管井降水效果较差,当管井内有0.02 MPa真空度,出水量较之无真空状态即有4倍左右的抬升,且每增加0.02 MPa的真空度,管井出水量便有25%左右的提升.当真空度达到0.08 MPa时,抽水30 d,出水总量可达47.68 m3,是真空度为0.02 MPa时出水总量的1.8倍.说明管井内的真空度越大, 与周围的土体间形成的等效水头差越大,地下水向管井渗流的速度得到加快,因此相同时间内出水总量得到提升.
3) 由图 6可知,10 m深的真空管井出水量极少,仅有0.067 m3/d, 这是由于10 m的高真空管井透水段仅有6 m,且井壁过水断面穿透的土层都是渗透系数很小的淤泥及淤泥质黏土(渗透系数在10-7 cm/s数量级),致管井出水量很小.20 m深的管井因穿透过一段渗透系数较高的粉质黏土夹粉砂层(渗透系数为10-5 cm/s数量级),较10 m的管井出水量增大100多倍,达8.96 m3/d.当井深继续增加至30 m时,可达43.2 m3/d的出水量,因井深30 m时已达渗透系数较高的含水层⑤3砂质粉土层(渗透系数在10-4 cm/s数量级),出水量上升明显.
可见土体渗透系数大小是一定时间内影响管井出水量的重要因素.
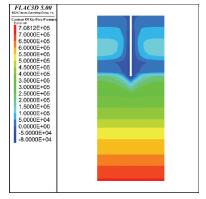
2.3.2 单井孔隙水压力变化规律图 7给出管井内真空度为0.08 MPa时抽水1 d后的单井孔压分布云图,图 8给出了管井内真空度为0.08 MPa时抽水30 d后的单井孔压分布云图.

|
图 7 抽水1 d孔压分布 Figure 7 Contours of pore pressure after 1 day pumping |
|
图 8 抽水30 d孔压分布 Figure 8 Contours of pore pressure after 30 days pumping |
1) 图 7与图 8对比发现,降水初始时出水量较大,管井周围很快形成一定的负压区,随降水时间的推进,负压区会向着真空管井上部4 m的不透水段周围土体扩散,形成一个小范围的漏斗状负压分布.真空负压在淤泥质黏土中总体传递缓慢且传递范围较小.当降水时间达30 d时,负压分布区域会比降水初始时扩大5~6倍,从两图比较中可以明显看到负压在淤泥质黏土中的传递过程.降水1 d时在井下部土层中负孔压集中分布在井周1 m范围内,随降水时间增加,负压先沿着水平方向传递,再沿竖直方向上下扩散,在降水达30 d时孔压分布达到稳定,这时水平向负压影响半径在5 m左右.负压在低渗透性淤泥质黏土中先沿管井顶部所在土层水平方向传递,之后再顺管壁在土中竖直方向传递,可见真空度在土中水和空气被排出的水位面以上区域传递较快,而负压继续向水位面以下区域传递时,由于真空渗流场中传递介质基本为水,而淤泥质黏土中地下水流动很困难,导致真空负压传递速度比较缓慢且范围较小.另外负压在③2粉质黏土夹粉砂土层中扩散速度及范围都明显增大,说明较高渗透系数有利于负压传递.
2) 管井内真空度大小对孔压分布的影响有以下两点:一是高真空管井(0.08 MPa)周围负压的分布范围是低真空管井(0.02 MPa)的1.4倍左右;二是高真空管井负压传递更快.上述现象是因为负压越大,地下水汇集速度越快,即土中孔隙水压力变化的速度更快,使得负压在土体中的传递效率得到提升,真空渗流场的影响范围随之加大.
3) 井深对于孔压分布的影响在于井深越大,负压的影响范围越大.管井下部渗透性较高的③2粉质黏土夹粉砂层、⑤3砂质粉层中负压扩散更快.上述结果反映出井深越大,管井过水断面越大,穿透渗透系数较高的含砂层,出水量与负压的分布范围都大幅提升.另外,上部淤泥质黏土的低渗透性,有利于维持井内及井周的高真空度,一定程度提高抽水效率.
2.3.3 井间距对出水量及孔压分布规律的影响以下数值模拟基于现场试验中的实际基坑尺寸,即20 m×20 m的降水区域,18 m深的高真空降水井,井内最大真空度为0.08 MPa.研究井中心间距分别为2、4、6、8、10 m时,计算降水时间为30 d的双井出水量规律.图 9给出单井日平均出水量随两井间距的变化曲线,图 10~12分别给出双井间距为4、8、10 m降水时间达1 d时的孔压分布云图,图 13给出双井间距为8 m降水30 d时的孔压分布云图.

|
图 9 日平均出水量随井距的变化曲线 Figure 9 The change of discharge per day with the distance of the double wells |
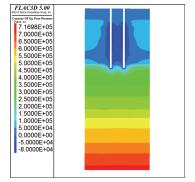
|
图 10 双井间距4 m时孔隙水压力云图 Figure 10 Contours of pore pressure of 4 m |

|
图 11 双井间距8 m时孔隙水压力云图 Figure 11 Contours of pore pressure of 8 m |
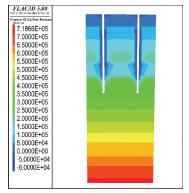
|
图 12 双井间距10 m时孔隙水压力云图 Figure 12 Contours of pore pressure of 10 m |

|
图 13 双井间距8 m时30 d孔隙水压力云图 Figure 13 Contours of pore pressure of 8 m after 30 days |
1) 根据图 9,当井间距为2 m时,每口井的日平均出水量为3.68 m3/d,当井间距增加到6 m时,每口井日平均出水量增加到4.48 m3/d, 且随两个真空井间距的增大,降水的影响区域增大,远处降深增加,该现象与文献[15]的试验结果吻合.当井间距进一步增大到8 m时,每口井日平均出水量增加至4.61 m3/d.井距越大,两井越接近各自独立降水的状态,出水总量得到提升.当井间距较小,每口井的出水量会较少,这是由于降水井的影响范围相互叠加,单井出水量受到周围井的影响,因此高真空群井设置间距不宜过小.因文中建立的数值模型基于现场试验中的实际基坑,此模型尺寸下当井间距增大到10 m时,单个井距离模型外边界只有5 m,无法避免会受到边界(基坑挡水帷幕)的影响,且此时双井间的真空负压叠加区域范围较小,不能起到加大水力梯度的作用,单井日平均出水量较间距为8 m时有所下降.所以在本文的宁波地铁樱花公园站土层下,400 m2区域内双井间距应该保持在8m左右.
图 9曲线为抽水30 d下的单井日平均出水量,计算过程中发现,抽水7 d之后,日平均出水量随时间增加略有减少,但变化不大,即图 9曲线沿y轴略有下移,但是曲线拐点横坐标基本不变,说明8 m间距在本案例中为合理双井间距.
2) 由图 10~12可知,当井间距为4~6 m时,井间土体中的负压会有较大范围的叠加区,双井下孔隙水压力传递较为快速,当双井间距为8 m(见图 11),抽水1 d,两井间的负压区还未有明显交集,可见孔压尚未完全稳定,随时间增长负孔压仍在向外扩散.观察图 13,当降水时间达到30 d时,两真空井中间的负压区明显扩大且下部的粉质黏土夹粉砂层中的水已经被大量排出,孔压分布达到稳定.从图 12可知,双井间距为10 m时,两井的影响范围交集过小,基本可看作两个独立的井在降水,无法利用真空叠加区加速渗流.因此,在宁波地铁樱花公园站场地条件下,高真空降水井间距应设置在8 m左右.
3 结论1) 土体的渗透系数对于降水效果有重要影响,低渗透性黏土中管井出水困难.管井内真空度大小对于出水量影响较明显,维持较高的真空度对于加大降水速率有作用,而高真空双管疏干井结构可以有效保持内外管间的高真空度.
2) 真空负压在低渗透性淤泥质黏土中于水位面以上传递速度较快,在水位面以下传递受限,淤泥质黏土层有利于真空度长时间的维持.
3) 在本文给定的土层条件下,400 m2区域的井间距建议设置在8 m左右,布置2口井为宜.
| [1] |
赵斌, 陈朝文, 王俊涛. 低渗透性黏土层中超真空双管疏干井降水技术的研究[J]. 建筑施工, 2015, 37(4): 422-423, 470. ZHAO Bin, CHEN Chaowen, WANG Juntao. Study on low permeability clay layer in high vacuum tube drainage wells precipitation technology[J]. Building Construction, 2015, 37(4): 422-423, 470. |
| [2] |
CASHMAN P M, PREENE M. Groundwater Lowering in Construction[M]. New York: CRC Press Inc, 2013: 285-313.
|
| [3] |
杨海旭, 王海飙, 董希斌. 真空井点降水联合加固软土地基的试验[J]. 哈尔滨工业大学学报, 2008, 40(12): 2044-2047. YANG Haixu, WANG Haibiao, DONG Xibin. Experimental study on the combined method of vacuum well-point dewatering and preloading[J]. Journal of Harbin Institute of Technology, 2008, 40(12): 2044-2047. DOI:10.3321/j.issn:0367-6234.2008.12.041 |
| [4] |
周念清, 唐益群, 娄荣祥, 等. 徐家汇地铁站深基坑降水数值模拟与沉降控制[J]. 岩土工程学报, 2011, 33(12): 1950-1956. ZHOU Nianqing, TANG Yiqun, LOU Rongxiang, et al. Numerical simulation of deep foundation pit dewatering and land subsidence control of Xujiahui Metro Station[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1950-1956. |
| [5] |
黄峰. 真空管井降水机理研究[D]. 北京: 中国地质大学, 2014. HUANG Feng. Study on the dewatering mechanism of vacuum tube[D]. Beijing: China University of Geosciences, 2014. |
| [6] |
贾向新, 聂庆科, 王英辉, 等. 真空井点降水试验分析与数值模拟[J]. 岩土力学, 2014, 35(增刊): 1950-1956. JIA Xiangxin, NIE Qingke, WANG Yinghui, et al. Analysis and numerical simulation of vacuum well point dewatering test[J]. Rock and Soil Mechanics, 2014, 35(s): 1950-1956. |
| [7] |
LI Lihui, WANG Qing, WANG Nianxiang, et al. Vacuum dewatering and horizontal drainage blankets: a method for layered soil reclamation[J]. Bulletin of Engineering Geology and the Environment, 2009, 68(2): 277-285. DOI:10.1007/s10064-009-0200-7 |
| [8] |
HUANG Feng, WANG Guihe. The influence of air injection on effects of vacuum dewatering: experimental study on vacuum-air injection dewatering method[J]. Electronic Journal of Geotechnical Engineering, 2012, 17: 2913-2923. |
| [9] |
张冬冬, 陈龙珠, 孙瑞瑞. 真空疏干降水与地表变形控制数值模拟研究[J]. 湖北大学学报, 2017, 39(3): 264-269. ZHANG Dongdong, CHEN Longzhu, SUN Ruirui. Numerical simulation of vacuum dewatering and surface deformation control[J]. Journal of Hubei University, 2017, 39(30): 264-269. |
| [10] |
CASTELLETTO N, GAMBOLATI G. A fully coupled 3-D mixed finite element model of Biot consolidation[J]. Journal of Computational Physics, 2010, 229(12): 4813-4830. DOI:10.1016/j.jcp.2010.03.018 |
| [11] |
HUANG Feng, WANG Guihe. One-dimensional experiment research on vacuum degree transmission law in unsaturated Soil[J]. Electronic Journal of Geotechnical Engineering, 2012, 17: 3313-3322. |
| [12] |
INDRARATNA B, REDANA I. Numerical modeling of vertical drain with smear and well resistance installed in soft clay[J]. Canadian Geotechnical Journal, 2000, 37(2): 132-145. DOI:10.1139/t99-115 |
| [13] |
李毅, 伍嘉, 李坤. 基于FLAC3D的饱和-非饱和渗流分析[J]. 岩土力学, 2012, 33(2): 617-622. LI Yi, WU Jia, LI Kun. Saturated-unsaturated seepage analysis based on FLAC3D[J]. Rock and Soil Mechanics, 2012, 33(2): 617-622. |
| [14] |
WANG Jianxiu, HU Lisheng, WU Lingao, et al. Hydraulic barrier function of the underground continuous concrete wall in the pit of metro station and its optimization[J]. Environmental Geology, 2009, 57: 447-453. DOI:10.1007/s00254-008-1315-z |
| [15] |
聂庆科, 王英辉, 白冰, 等. 单井点和单排井点布置的真空降水现场试验及比较研究[J]. 岩土力学, 2014, 35(2): 481-489. NIE Qingke, WANG Yinghui, BAI Bing, et al. Field test and comparative study of vacuum dewatering with single well point and single well location[J]. Rock and Soil Mechanics, 2014, 35(2): 481-489. |
 2018, Vol. 50
2018, Vol. 50


