高速公路路基的侧向位移、高边坡的侧向变形和基坑的侧壁稳定等工程力学关注的变形和强度性质中,均存在与剪切流变特性相关的时间效应问题[1-3].陈宗基[1]发现剪切蠕变变形是荷兰Wlaggemans大桥竣工两年后发生破坏的主要原因后,深刻意识到流变特性在岩土力学中的重要性,在国内外率先提出岩土流变力学.Singh等[4]和Mesri等[5]基于三轴固结排水和不排水蠕变试验,分别提出了软土的指数型和双曲线型剪应变蠕变经验公式.刘加才等[6]和周秋娟等[7]采用弹簧和黏壶等力学元件组合来建立软土的体应变和剪应变流变模型.Yin J H等[8]和Yin Z Y等[9]利用体应变流变方程和剑桥模型屈服准则来揭示非线性剪切流变性质.然而上述研究仍留存一些不完善的情况:1)Singh-Mitchell[4]和Mesri[5]经验公式只适用于恒定修正应力水平作用,难以预测变修正应力水平作用下的蠕变变形量; 2)力学元件组合流变模型只适用于线性流变特性,与软土非线性流变特性差别较大; 3)从Buisman公式[8]看体应变蠕变经验公式不存在时间与应力耦合项,而从Singh-Mitchell公式[4]看剪应变蠕变经验公式存在时间与应力耦合项.这说明剪应变流变特性具有自身特殊规律,以体应变流变速率方程和剑桥屈服准则为基础的弹黏塑性模型[8-9]难以反映它的性质.事实上,摩尔-库伦屈服准则、Matsuoka-Nakai三剪应力屈服准则和Lade屈服准则在岩土工程界得到广泛应用[10].这些屈服准则以剪应变为硬化参数,能够充分反映土的剪胀性.为了与这些岩土屈服准则相匹配,需要建立剪切流变速率直接与剪应力和黏塑性剪应变相关的流变方程,进一步完善软土弹黏塑性本构模型体系.
鉴于上述研究现状,本文采用等效时间法[11],通过修正后的Singh-Mitchell剪应变蠕变经验公式,建立了一个适用于变剪应力作用和非线性特性的等效时间线剪切弹黏塑性流变模型;通过模拟三轴固结排水试验数据,显示它能较好地模拟多级加载软土剪切蠕变试验成果.
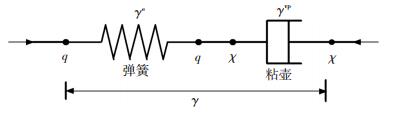
1 等效时间线剪切流变模型 1.1 采用绝对等效时间表示的流变模型表达式与Yin-Graham等效时间线体应变弹黏塑性模型[11]一样,如图 1所示,本文也选用非线性弹簧和黏壶组成的Maxwell模型来反映软土的流变特性.从图 1可知,剪应变可表示为弹性应变和黏塑性应变之和:
|
图 1 软土弹黏塑性模型元件组合图 Figure 1 Diagram of element combination for elasto-viscoplastic model |
| $ \gamma = {\gamma ^{\rm{e}}} + {\gamma ^{{\rm{vp}}}},\;\;\;\;\;即:\dot \gamma = {{\dot \gamma }^{\rm{e}}} + {{\dot \gamma }^{{\rm{vp}}}}. $ | (1) |
式中:γ为广义剪应变,简称剪应变,γe为弹性剪应变,γvp为黏塑性剪应变.
假定剪切弹性应力应变关系符合胡克定律,有:
| $ {\gamma ^{\rm{e}}} = \frac{q}{{3G}},即{{\dot \gamma }^{\rm{e}}} = \frac{{\dot q}}{{3G}}. $ | (2) |
式中:q为广义剪应力,简称剪应力,G为弹性剪切模量.
按照热力学内变量连续介质理论[12],
| $ {{\dot \gamma }^{{\rm{vp}}}} = f\left( {D,{\gamma ^{{\rm{vp}}}}} \right). $ | (3) |
式中:D=q/qf,本文把它称为修正应力水平,由于岩土材料的式(3)表达式往往比较复杂,难以根据试验数据直接归纳确定.但对于一些简单加载工况,已经总结出许多剪应变蠕变公式,如Singh-Mitchell[4]和Mesri[5]剪应变蠕变经验公式等等.如果能够根据这些经验公式获得式(3),就可以把它用于软土剪切弹黏塑性本构方程的建模工作.
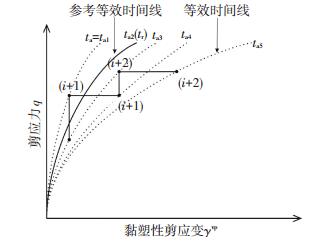
剪切流变等效时间线如图 2示意图所示.考虑到剪应力等于零时剪切蠕变量也为零,为了扩大Singh-Mitchell剪切蠕变经验公式的应用范围,把常修正应力水平下软土黏塑性剪应变随时间变化规律修正为
|
图 2 黏土的剪切蠕变示意 Figure 2 Shear creep diagram of clay |
| $ {\gamma ^{{\rm{vp}}}} = \gamma _{\rm{a}}^{{\rm{vp}}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]{\left( {\frac{{{t_{\rm{a}}}}}{{{t_{\rm{r}}}}}} \right)^m}. $ | (4) |
式中:γavp为黏塑性剪应变特征常数,ta为常修正应力水平下蠕变的持续时间,tr为参考时间,Br为基于参考时间tr的黏塑性剪切系数,α为修正应力水平影响系数,m为黏塑性剪切指数.
对式(4)按时间求导得
| $ {{\dot \gamma }^{{\rm{vp}}}} = \frac{{m{B_{\rm{r}}}}}{{t_{\rm{r}}^m}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]t_{\rm{a}}^{m - 1}. $ | (5) |
根据式(4)又可得
| $ {t_{\rm{a}}} = {t_{\rm{r}}}{\left\{ {\frac{{{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{a}}^{{\rm{vp}}}}}{{{B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]}}} \right\}^{\frac{1}{m}}}. $ | (6) |
把式(6)代入到式(5)得
| $ {{\dot \gamma }^{{\rm{vp}}}} = \frac{m}{{{t_{\rm{r}}}}}{\left\{ {{B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]} \right\}^{\frac{1}{m}}}{\left( {{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{a}}^{{\rm{vp}}}} \right)^{\frac{{m - 1}}{m}}}. $ | (7) |
由于式(4)中的D和γvp涵盖了实际可能发生的所有修正应力水平和黏塑性剪应变,故根据式(7)可以获得与任意一对(D, γvp)相对应的黏塑性剪应变速率.根据式(3)假定,软土的黏塑性剪应变速率唯一地取决于修正应力水平和黏塑性剪应变;因此式(7)必须与式(3)相同,否则就会出现同一对(D, γvp)值对应于两个不同
由于式(7)与式(3)相同,故式(7)可以用于任意一种加载历史(加载工况).从式(4)推出式(7)的过程中,ta起到了中间桥梁的关键作用,同时,式(4)中的ta值具有不会随着参考时间tr取值的改变而改变的优良性质,因此把ta称为绝对等效时间,相应地tr称为参考等效时间.把式(4)称为黏塑性剪应变—剪应力—绝对等效时间之间存在的唯一性关系方程.把式(2)和式(7)代入到式(1)中的第二式得
| $ \dot \gamma = \frac{{\dot q}}{{3G}} + \frac{m}{{{t_{\rm{r}}}}}{\left\{ {{B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]} \right\}^{\frac{1}{m}}}{\left( {{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{a}}^{{\rm{vp}}}} \right)^{\frac{{m - 1}}{m}}}. $ | (8) |
式(8)是基于绝对等效时间的软土剪切弹黏塑性模型.
1.2 采用相对等效时间表示的流变模型表达式在某些条件下,已知ta=tr和D=Dr时的黏塑性剪应变γrvp,此时根据式(4)可得
| $ \gamma _{\rm{a}}^{{\rm{vp}}} = \gamma _{\rm{r}}^{{\rm{vp}}} - {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_{\rm{r}}}} \right) - 1} \right]. $ | (9) |
定义相对等效时间te为绝对等效时间与参考等效时间之差,故有
| $ {t_{\rm{e}}} = {t_{\rm{a}}} - {t_{\rm{r}}}. $ | (10) |
等效时间te值会随着参考时间tr取值的改变而发生改变,具有相对等效时间的性质,与文献[11]一样把它简称为等效时间.把式(10)代入式(4)得
| $ \begin{array}{l} {\gamma ^{{\rm{vp}}}} = \gamma _{\rm{r}}^{{\rm{vp}}} - {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_{\rm{r}}}} \right) - 1} \right] + \\ \;\;\;\;\;\;\;\;{B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]{\left( {\frac{{{t_{\rm{r}}} + {t_{\rm{e}}}}}{{{t_{\rm{r}}}}}} \right)^m}. \end{array} $ | (11) |
把式(9)代入到式(8)可得基于参考点(Dr, tr)的剪切流变方程为
| $ \begin{array}{*{20}{c}} {\dot \gamma = \frac{{\dot q}}{{3G}} + \frac{m}{{{t_{\rm{r}}}}}{{\left\{ {{B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]} \right\}}^{\frac{1}{m}}} \times }\\ {{{\left\{ {{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{r}}^{{\rm{vp}}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_{\rm{r}}}} \right) - 1} \right]} \right\}}^{\frac{{m - 1}}{m}}}.} \end{array} $ | (12) |
式(12)是基于tr线上参考点的剪切弹黏塑性模型.当然,式(12)与式(8)是相互等价的.
2 特定条件下的流变方程解 2.1 完全排水条件下单级施荷时的流变方程解设t=0时土体所处的绝对等效时间为ta0,剪应力为q0,破坏剪应力为qf0,修正应力水平为D0=q0/qf0,剪应变为γ0.现分析三轴固结排水试验中围压σ3保持不变时剪应力从q0瞬时加载到q时的流变方程解.
完全排水条件下的超孔压接近于零,故有效应力σ′3等于围压σ3,根据摩尔-库伦强度准则可知破坏剪应力与有效围压σ′3之间的关系为
| $ {q_{\rm{f}}} = {{K'}_{\rm{p}}}{{\sigma '}_3} + C' = {{K'}_{\rm{p}}}{\sigma _3} + C'. $ | (13) |
令φ′为有效内摩擦角,c′为黏聚力,在式(13)中:
| $ {{K'}_{\rm{p}}} = \frac{{2\sin \varphi '}}{{1 - \sin \varphi '}},C' = \frac{{2\cos \varphi '}}{{1 - \sin \varphi '}}c'. $ | (14) |
由于σ3保持不变,同一种土的K′p和C′也是常数,故qf=qf0也保持不变.
第一步,瞬时加载过程.由于剪应力从q0到q是瞬时加载的,加载过程的用时为0,故瞬时加载前后的时间t都为零.对式(8)积分求解得
| $ {\gamma _1} = {\gamma _0} + \frac{{q - {q_0}}}{{3G}}. $ | (15) |
设瞬时加载到q时的绝对等效时间为ta1m,相应的黏塑性剪应变为γ1vp.把唯一性关系方程式(4)用于瞬时加载结束工况,有:
| $ \gamma _1^{{\rm{vp}}} = \gamma _{\rm{a}}^{{\rm{vp}}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]{\left( {\frac{{{t_{{\rm{a1}}}}}}{{{t_{\rm{r}}}}}} \right)^m}. $ | (16) |
根据瞬间加载前后黏塑性剪应变不变性质和式(4),有:
| $ {t_{{\rm{a1}}}} = {t_{{\rm{a0}}}}{\left[ {\frac{{\exp \left( {\alpha {D_0}} \right) - 1}}{{\exp \left( {\alpha D} \right) - 1}}} \right]^{\frac{1}{m}}}. $ | (17) |
第二步,当t>0时,是恒定修正应力水平下的蠕变变形.由式(13)可知剪应力也恒定,根据式(8)可得:
| $ \frac{{{\rm{d}}\left( {{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{a}}^{{\rm{vp}}}} \right)}}{{m{{\left( {{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{a}}^{{\rm{vp}}}} \right)}^{\frac{{m - 1}}{m}}}}} = \frac{1}{{{t_{\rm{r}}}}}{\left\{ {{B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]} \right\}^{\frac{1}{m}}}{\rm{d}}t. $ | (18) |
求解式(18)得
| $ {\gamma ^{{\rm{vp}}}} = \gamma _{\rm{a}}^{{\rm{vp}}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]{\left( {\frac{{t + {t_{{\rm{a1}}}}}}{{{t_{\rm{r}}}}}} \right)^m}. $ | (19) |
由于该阶段的剪应力保持不变,所以弹性剪应变等于瞬时加载到q时的弹性剪应变.令γ1e为瞬时加载到q时的弹性剪应变,根据γ1=γ1e+γ1vp和式(15)有
| $ {\gamma ^{\rm{e}}} = \gamma _1^{\rm{e}} = {\gamma _0} + \frac{{q - {q_0}}}{{3G}} - \gamma _1^{{\rm{vp}}}. $ | (20) |
令:
| $ \gamma _{{\rm{a0}}}^{{\rm{vp}}} = {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_0}} \right) - 1} \right]{\left( {\frac{{{t_{{\rm{a0}}}}}}{{{t_{\rm{r}}}}}} \right)^m}. $ | (21) |
由式(16)~(17)、式(19)、式(20)~(21)和γ=γe+γvp得
| $ \gamma = {\gamma _0} + \frac{{q - {q_0}}}{{3G}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]{\left( {\frac{{t + {t_{{\rm{a1}}}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (22) |
式(22)即是完全排水条件下单级瞬时施加剪应力的流变方程解.
2.2 完全排水条件下多级加载时的流变方程解设t=0时土体的初始条件如2.1节,现求三轴固结排水试验中围压σ3保持不变时剪应力从q0开始瞬时施加到q1后维持时间tc1,然后瞬时施加到q2后维持时间tc2,...然后瞬时施加到qn后维持tcn,...直到施加到qN后剪应变随时间变化的流变方程解.
根据式(13)可知围压σ3保持不变时qf也保持不变.令D1=q1/qf,根据式(22)可得剪应力从q0瞬时施加到q1后维持时间tc1时的剪应变为
| $ \begin{array}{l} {\gamma _1} = {\gamma _0} + \frac{{{q_1} - {q_0}}}{{3G}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_1}} \right) - 1} \right] \times \\ \;\;\;\;\;\;\;{\left( {\frac{{{t_{{\rm{c1}}}} + {t_{{\rm{a1}}}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. \end{array} $ | (23) |
令D2=q2/qf,由于剪应力从q1瞬时施加到q2的过程中所用的时间为零,从式(15)可知在这个过程中只有弹性变形而无黏塑性变形,故瞬时施加到q2时的黏塑性剪应变等于加载前q1荷载下维持时间tc1时的黏塑性剪应变.由此根据式(16)和式(19)可得:
| $ \gamma _{\rm{2}}^{{\rm{vp}}} = \gamma _{\rm{0}}^{{\rm{vp}}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_1}} \right) - 1} \right]{\left( {\frac{{{t_{{\rm{c1}}}} + {t_{{\rm{a1}}}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (24) |
根据瞬时施加到q2前后的唯一性关系方程式(4),可得瞬时施加到q2时的绝对等效时间ta2为
| $ {t_{{\rm{a2}}}} = {t_{{\rm{c1}}}}{\left[ {\frac{{\exp \left( {\alpha {D_1}} \right) - 1}}{{\exp \left( {\alpha {D_2}} \right) - 1}}} \right]^{\frac{1}{m}}} + {t_{{\rm{a0}}}}{\left[ {\frac{{\exp \left( {\alpha {D_0}} \right) - 1}}{{\exp \left( {\alpha {D_2}} \right) - 1}}} \right]^{\frac{1}{m}}}. $ | (25) |
重复2.1节中从式(18)~(22)的推导过程,可得瞬时施加到q2后维持时间tc2时的剪应变为
| $ {\gamma _2} = {\gamma _0} + \frac{{{q_2} - {q_0}}}{{3G}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_2}} \right) - 1} \right]{\left( {\frac{{{t_{{\rm{c2}}}} + {t_{{\rm{a2}}}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (26) |
以此类推,令Dn=qn/qf,从qn-1瞬时施加到qn时的黏塑性剪应变为
| $ \gamma _n^{{\rm{vp}}} = \gamma _{\rm{0}}^{{\rm{vp}}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_{n - 1}}} \right) - 1} \right]{\left( {\frac{{{t_{{\rm{c}}\left( {n - 1} \right)}} + {t_{{\rm{a}}\left( {n - 1} \right)}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (27) |
相应的绝对等效时间tan为
| $ {t_{{\rm{a}}n}} = \sum\limits_{i = 1}^{n - 1} {{t_{{\rm{c}}i}}{{\left[ {\frac{{\exp \left( {\alpha {D_i}} \right) - 1}}{{\exp \left( {\alpha {D_n}} \right) - 1}}} \right]}^{\frac{1}{m}}} + {t_{{\rm{a0}}}}{{\left[ {\frac{{\exp \left( {\alpha {D_0}} \right) - 1}}{{\exp \left( {\alpha {D_n}} \right) - 1}}} \right]}^{\frac{1}{m}}}.} $ | (28) |
瞬时施加到qn后维持时间tcn时的剪应变为
| $ {\gamma _n} = {\gamma _0} + \frac{{{q_n} - {q_0}}}{{3G}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_n}} \right) - 1} \right]{\left( {\frac{{{t_{{\rm{c}}n}} + {t_{{\rm{a}}n}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (29) |
故当n=N时,设多级加载从q0开始的总持续时间为t,则从瞬时加载qN后起算的持续时间为
| $ {t_N} = t - \sum\limits_{i = 1}^{N - 1} {{t_{{\rm{c}}i}}} . $ | (30) |
故施加到qN后剪应变随时间变化的流变方程解为
| $ {\gamma _N} = {\gamma _0} + \frac{{{q_N} - {q_0}}}{{3G}} + {B_{\rm{r}}}\left[ {\exp \left( {\alpha {D_N}} \right) - 1} \right]{\left( {\frac{{{t_N} + {t_{{\rm{a}}N}}}}{{{t_{\rm{r}}}}}} \right)^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (31) |
设t=0时的初始条件与2.1节相同.现在研究常规三轴条件下有效围压和剪应力分别按σ′3(t)和q(t)变化时的流变方程解.
由式(13)可知qf与σ′3(t)的关系为
| $ {q_{\rm{f}}} = {{K'}_{\rm{p}}}{{\sigma '}_3}\left( t \right) + C'. $ | (32) |
把式(32)和q(t)代入到式(8)并利用γ=γe+γvp得
| $ \begin{array}{l} {\rm{d}}\left[ {{{\left( {{\gamma ^{{\rm{vp}}}} - \gamma _{\rm{a}}^{{\rm{vp}}}} \right)}^{\frac{1}{m}}}} \right] = \\ \;\;\;\;\frac{1}{{{t_{\rm{r}}}}}{\left\{ {{B_{\rm{r}}}\left[ {\exp \left( {\alpha \frac{{q\left( t \right)}}{{{K_{\rm{p}}}{{\sigma '}_3}\left( t \right) - q\left( t \right) + C'}}} \right) - 1} \right]} \right\}^{\frac{1}{m}}}{\rm{d}}t. \end{array} $ | (33) |
令:
| $ {F_{\rm{t}}}\left( t \right) = \int_0^t {{{\left[ {\exp \left( {\alpha \frac{{q\left( t \right)}}{{{K_{\rm{p}}}{{\sigma '}_3}\left( t \right) - q\left( t \right) + C'}}} \right) - 1} \right]}^{\frac{1}{m}}}{\rm{d}}t} . $ | (34) |
对初始条件运用式(4)和式(21)可得γavp=γ0vp-γa0vp.对式(33)求解并利用式(34)和γavp=γ0vp-γa0vp得
| $ {\gamma ^{{\rm{vp}}}} - \gamma _0^{{\rm{vp}}} = {B_{\rm{r}}}{\left[ {\frac{{{F_{\rm{t}}}\left( t \right)}}{{{t_{\rm{r}}}}} + {{\left( {\frac{{\gamma _{{\rm{a0}}}^{{\rm{vp}}}}}{{{B_{\rm{r}}}}}} \right)}^{\frac{1}{m}}}} \right]^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (35) |
根据
| $ \gamma = {\gamma _0} + \frac{{q\left( t \right) - {q_0}}}{{3G}} + {\gamma ^{{\rm{vp}}}} - \gamma _0^{{\rm{vp}}}. $ | (36) |
把式(35)代入到式(36)得
| $ \gamma = {\gamma _0} + \frac{{q\left( t \right) - {q_0}}}{{3G}} + {B_{\rm{r}}}{\left[ {\frac{{{F_{\rm{t}}}\left( t \right)}}{{{t_{\rm{r}}}}} + {{\left( {\frac{{\gamma _{{\rm{a0}}}^{{\rm{vp}}}}}{{{B_{\rm{r}}}}}} \right)}^{\frac{1}{m}}}} \right]^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. $ | (37) |
现在用式(37)分析三轴固结不排水试验中的剪切蠕变发展规律.设多级剪应力的加载方式为:保持围压σ3不变,剪应力从q0开始瞬时施加到q1后维持时间tc1,然后瞬时施加到q2后维持时间tc2,再瞬时施加到q3维持时间tc3,...瞬时施加到qn后维持tcn,…直到施加到qN.设多级加载从q0开始起算的总持续时间为t,则从加载qn后起算的持续时间为
| $ {t_n} = t - \sum\limits_{i = 1}^{n - 1} {{t_{{\rm{c}}i}}} . $ | (38) |
借鉴钱寿易和符圣聪提出的三轴固结不排水试验的孔压经验公式[13],建议多级加载过程中孔压随时间的变化规律可近似按如下公式进行计算:
| $ \begin{array}{*{20}{c}} {{U_n}\left( {{t_n}} \right) = {U_{n - 1}}\left( {{t_{{\rm{c}}\left( {n - 1} \right.}}} \right) + \beta \frac{{{q_n} - {q_{n - 1}}}}{3} + }\\ {\beta \left\{ {\left[ {{b_{\rm{c}}}\frac{{{q_n}}}{{{q_{{\rm{f0}}}}}} - {a_{\rm{c}}}{{\left( {\frac{{{q_n}}}{{{q_{{\rm{f0}}}}}}} \right)}^2}} \right]{q_n} - {U_{n - 1}}} \right\}\frac{{{t_n}}}{{{t_n} + {t_{\rm{c}}}}}.} \end{array} $ | (39) |
式中:Un-1为上一级荷载结束时的孔压,U0=0;β为Skempton系数,对于饱和土取β=1.0;bc、ac和tc是与土性有关的系数.令:
| $ \left\{ \begin{array}{l} {a_n} = \beta \left\{ {\left[ {{b_{\rm{c}}}\frac{{{q_n}}}{{{q_{{\rm{f0}}}}}} - {a_{\rm{c}}}{{\left( {\frac{{{q_n}}}{{{q_{{\rm{f0}}}}}}} \right)}^2}} \right]{q_n} - {U_{n - 1}}} \right\},\\ {b_n} = {\sigma _3} - {U_{n - 1}}\left( {{t_{{\rm{c}}\left( {n - 1} \right.}}} \right) - \beta \frac{{{q_n} - {q_{n - 1}}}}{3} - {a_n}. \end{array} \right. $ | (40) |
则第n级剪应力qn作用下有效围压σ′3(t)随时间的变化规律为
| $ {{\sigma '}_3}\left( t \right) = {\sigma _3} - {U_n}\left( {{t_n}} \right) = {b_n} + \frac{{{a_n}{t_{\rm{c}}}}}{{{t_n} + {t_{\rm{c}}}}}. $ | (41) |
令:
| $ {F_{\rm{t}}}\left( t \right) = \sum\limits_{n = 1}^{N - 1} {{F_{{\rm{t}}n}}\left( {{t_{{\rm{c}}n}}} \right) + {F_{{\rm{t}}N}}\left( {{t_N}} \right)} . $ | (42) |
把式(42)代入到式(37)可得第N级剪应力qN作用下剪应变随时间变化的流变方程解为
| $ \begin{array}{l} \gamma = {\gamma _0} + \frac{{q\left( t \right) - {q_0}}}{{3G}} + {B_{\rm{r}}}\left[ {\sum\limits_{n = 1}^{N - 1} {\frac{{{F_{{\rm{t}}n}}\left( {{t_{{\rm{c}}n}}} \right)}}{{{t_{\rm{r}}}}} + \frac{{{F_{{\rm{t}}N}}\left( {{t_N}} \right)}}{{{t_{\rm{r}}}}}} + } \right.\\ \;\;\;\;{\left. {{{\left( {\frac{{\gamma _{{\rm{a0}}}^{{\rm{vp}}}}}{{{B_{\rm{r}}}}}} \right)}^{\frac{1}{m}}}} \right]^m} - \gamma _{{\rm{a0}}}^{{\rm{vp}}}. \end{array} $ | (43) |
从式(8)流变模型本身看,需要5个模型参数,分别是:剪切弹性模量G、黏塑性剪应变特征常数γavp、基于参考时间tr的黏塑性剪切系数Br、修正应力水平影响系数α和黏塑性剪切指数m.
另外计算修正应力水平时需要确定破坏剪应力,需要2个土工参数:分别是有效内摩擦角φ′和黏聚力c′.
两者加起来共7个参数.这7个参数中,φ′和c′的确定方法与经典土力学相同.G可以根据式(15)通过剪应力和骤然加载时产生的瞬时剪应变之间的关系来确定,也可以根据卸载时剪应力与剪应变的关系来确定.地基承受的修正应力水平通常在10%~60%的范围内变化,考虑到岩土剪切弹性本构关系具有一定的非线性,故把G值取为修正应力水平10%~60%的剪切割线模量.
为方便地确定参数Br,不失一般性,本文把参考时间tr取为1天(1 d),用t1d=1 d来表示,并把与参考时间t1d=1 d对应的黏塑性剪切系数用B1d来表示.由于剪切流变方程是软土剪切流变客观规律的反映,它不会随着所选用的参考时间tr的变化而发生变化,因此当选用其它参考时间tr时,与tr对应的黏塑性剪切系数Br与B1d的关系应该满足下式:
| $ {B_{\rm{r}}}{\left( {\frac{1}{{{t_{\rm{r}}}}}} \right)^m} = {B_{{\rm{1d}}}}{\left( {\frac{1}{{{t_{{\rm{1d}}}}}}} \right)^m},即\;{B_r} = {B_{{\rm{1}}d}}{\left( {\frac{{{t_r}}}{{{t_{{\rm{1}}d}}}}} \right)^m}. $ | (44) |
式(44)表明,只要知道B1d值,就可以知道其它参考时间的Br,故只要确定B1d就可以了.
为了简化剪切流变模型表达式,本文假定剪应力等于零时蠕变为零,即γavp=0.故根据式(4)和式(44)得
| $ {\gamma ^{{\rm{vp}}}} = {B_{{\rm{1d}}}}\left[ {\exp \left( {\alpha D} \right) - 1} \right]{\left( {\frac{{{t_{\rm{a}}}}}{{{t_{{\rm{1d}}}}}}} \right)^m}. $ | (45) |
令γDvp=lnB1d+ln[exp(αD)-1],对式(45)两边求对数得
| $ \ln {\gamma ^{{\rm{vp}}}} = \gamma _{\rm{D}}^{{\rm{vp}}} + m\ln \left( {{t_{\rm{a}}}/{t_{{\rm{1d}}}}} \right). $ | (46) |
对于三轴排水试验,同一级剪应力的σ3不变,D值是一个常数,故γDvp也是一个常数,根据式(46)进行线性回归可以获得m和各个修正应力水平Di下的γDivp.
令B1d*=lnB1d,根据非线性回归分析理论[14],系数B1d*和α应当使
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {\gamma _{{\rm{D}}i}^{{\rm{vp}}} - NB_{{\rm{1d}}}^ * } - \sum\limits_{i = 1}^N {\ln \left[ {\exp \left( {\alpha {D_i}} \right) - 1} \right] = 0} ,\\ \sum\limits_{i = 1}^N {\frac{{{D_i}\exp \left( {\alpha {D_i}} \right)}}{{\exp \left( {\alpha {D_i}} \right) - 1}}\left\{ {\gamma _{{\rm{D}}i}^{{\rm{vp}}} - B_{{\rm{1d}}}^ * - \ln \left[ {\exp \left( {\alpha {D_i}} \right) - 1} \right]} \right\}} = 0. \end{array} \right. $ | (47) |
对式(47)采用改进的高斯-牛顿迭代法进行求解,可以获得B1d*和α,进而获得B1d和α.
3 算例验证福建省漳州市受九龙江洪流和潮汐影响,分布有深厚软弱地层,属第四系全新世海陆交互相软土,具有高压缩性、高灵敏度、低承载力和低强度等力学特性.为了深入了解和掌握漳州市九龙江河口区域软土的蠕变特性,张先伟对漳州市开发区内九龙江出海口南岸的粉质淤泥进行了三轴固结排水蠕变试验[15].试验土样的取样深度为14 m,深灰色,滑腻光滑,含有机质,稍具臭味,其基本力学性质如表 1所示.
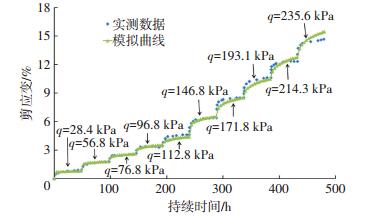
软土蠕变试验在三轴仪上按固结排水方案实施.选用的围压σ3分别为100 kPa、150 kPa和200 kPa.固结完成后保持σ3不变,再分级施加剪应力,各级剪应力作用下剪应变随时间发展的试验数据如图 3~5所示.
|
图 3 σ3=100 kPa时分级荷载下剪应变随时间变化曲线 Figure 3 Shear strain varying with time under multi-stage loading for σ3=100 kPa |
|
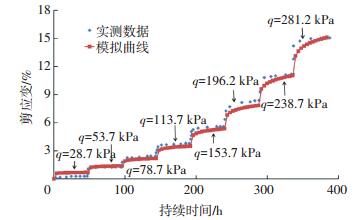
图 4 σ3=150 kPa时各级荷载下剪应变随时间变化曲线 Figure 4 Shear strain varying with time under multi-stage loading for σ3=150 kPa |
|
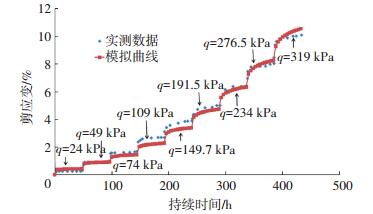
图 5 σ3=200 kPa时各级荷载下剪应变随时间变化曲线 Figure 5 Shear strain varying with time under multi-stage loading for σ3=200 kPa |
为了运用本文模型模拟图 3~5,需确定模型参数.首先,利用张先伟[15]实施的土工试验获得漳州软土的强度指标为φ′和c′,见表 2.其次,从图中可以看出,在每一级剪应力施加初期,剪应变随时间的变化较为迅速,随着时间增长,剪应变增长速度逐渐变慢.采用随时间幂函数变化模型能较为合适地反映各级剪应力作用下剪应变的增长规律.为此,把图 3中分级加载试验数据按照陈氏法[15]转化为分别加载试验数据,然后对分别加载试验数据按照式(45)~(46)和相同的m值进行线性回归分析,求得m=0.062 5和各级剪应力q作用下的γDvp值.根据式(13)~(14)和σ3计算qf值,然后根据q和D=q/qf计算D,由此可得图 6中“γDvp值”数据点.再利用式(47)进行非线性回归求得β1d=2.82和α=1.86,根据β1d和α值绘制成回归曲线如图 6所示.其它模式参数也可以按照第2.4节介绍的方法确定,并把它们全部汇总到表 2中,便于理论分析应用.
| 表 2 粉质淤泥的剪切弹黏塑性模型参数 Table 2 Parameters of shear elasto-viscoplastic model for silty sludge |
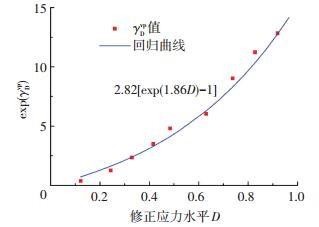
|
图 6 γDvp值及其回归曲线 Figure 6 Value of γDvp and its regression curve |
选用表 2所示的模型参数对试验结果进行模拟.由于表 2中β1d是基于24 h(1 d)测定的,而图 3~5中横坐标的单位是h,因此需要根据式(44)把β1d换成是参考时间为1 h的βr值,本文用β1h来表示,其值等于β1h=β1d(1/24)m=2.31.模拟结果表明,等效时间流变模型能较好地体现出剪切蠕变的如下发展特点:1)当围压保持不变时,随着修正应力水平的增加蠕变速率增大,剪应变增长幅值增快; 2)当修正应力水平保持不变时,随着围压的增加蠕变速率减小,剪应变增加幅值相应较小; 3)剪切蠕变量主要发生在剪应力施加初期阶段,随着时间增长,蠕变速率逐渐变慢.从图 3~5可以看出模型预测结果与试验数据相互之间较为吻合.
4 结论本文通过修正Singh-Mitchell剪应变蠕变经验公式,使之适用于低修正应力水平工况,利用Yin-Graham提出的等效时间法,建立了剪切弹黏塑性流变模型,获得了以下研究成果:
1) 发展了Yin-Graham提出的等效时间法.Yin和Graham根据黏塑性应变速率唯一地取决于应力与应变的性质提出体应变流变速率方程.本文吸收了非平衡态热力学在耗散空间中运用耗散热力学量建立材料不可逆本构方程的建模思想,根据黏塑性应变速率唯一地取决于耗散应力与黏塑性应变的性质建立剪应变流变速率方程,使等效时间法的物理概念更加严谨,扩大了等效时间法建立弹黏塑性本构模型的应用范围.
2) 根据修正Singh-Mitchell剪应变蠕变经验公式,建立了等效时间线剪切弹黏塑性流变模型,获得了完全排水条件下单级、多级加载的流变方程解以及围压和剪应力随时间任意变化条件下的流变方程解.
3) 采用本文模型与三轴固结排水分级加载剪切蠕变试验成果进行了对比,模型预测结果与试验数据较为吻合,说明本文模型具有实用性,具有反映剪应变随修正应力水平、有效围压和持续时间等影响因素变化规律的能力.
| [1] |
陈宗基. 对我国土力学、岩体力学中若干重要问题的看法[J]. 土木工程学报, 1963, 9(5): 24-30. CHEN Zongji. Views on some important problems in China soil and rock mechanics[J]. China Civil Engineering Journal, 1963, 9(5): 24-30. |
| [2] |
田光辉, 沈明荣, 周文锋, 等. 分级加载条件下的锯齿状结构面剪切松弛特性[J]. 哈尔滨工业大学学报, 2016, 48(12): 108-113. TIAN Guanghui, SHEN Mingrong, ZHOU Wenfeng, et al. Shear relaxation characteristic of serrate structure surface under stepwise loading[J]. Journal of Harbin institute of technology, 2016, 48(12): 108-113. DOI:10.11918/j.issn.0367-6234.2016.12.015 |
| [3] |
王振, 沈明荣, 顾琳琳. 以等应变速率曲线为基础的岩石长期强度确定方法[J]. 哈尔滨工业大学学报, 2017, 49(6): 77-83. WANG Zhen, SHEN Mingrong, GU Linlin. Methods for deter-mining long-term strength of rock based on iso-strain rate creep curves[J]. Journal of Harbin institute of technology, 2017, 49(6): 77-83. DOI:10.11918/j.issn.0367-6234.201602034 |
| [4] |
SINGH A, MITCHELL J K. General stress-strain-time function for clay[J]. Journal of the clay mechanics and Foundation Division, 1968, 94(SM1): 21-46. |
| [5] |
MESRI G, REBRES-CORDERO E, SCHIELDS D R, et al. Shear stress-strain-time behavior of clays[J]. Geotechnique, 1981, 31(4): 537-552. DOI:10.1680/geot.1981.31.4.537 |
| [6] |
刘加才, 赵维炳, 宰金珉, 等. 双层黏弹性地基一维固结分析[J]. 岩土力学, 2007, 28(4): 743-746. LIU Jiacai, ZHAO Weibing, ZAI Jinmin, et al. Analysis of one-dimensional consolidation of double-layered viscoelastic ground[J]. Rock and Soil Mechanics, 2007, 28(4): 743-746. |
| [7] |
周秋娟, 陈晓平. 典型基坑开挖卸荷路径下软土三轴流变特性研究[J]. 岩土力学, 2013, 34(5): 1299-1305. ZHOU Qiujuan, CHEN Xiaoping. Research on rheological properties of soft clay under typical pit unloading paths[J]. Rock and Soil Mechanics, 2013, 34(5): 1299-1305. |
| [8] |
YIN J H. Fundamental issues of constitutive modelling of the time dependent stress-strain behavior of geomaterials[J]. International Journal of Geomechanics, 2015, 15(5): A4015002, 1-9. |
| [9] |
YIN Z Y, CHANG C S, KARSTUNEN M, et al. An anisotropic elastic viscoplastic model for soft clays[J]. International Journal of Solids and Structures, 2010, 47(5): 665-677. DOI:10.1016/j.ijsolstr.2009.11.004 |
| [10] |
龚晓南. 土塑性力学[M]. 杭州: 浙江大学出版社, 2001: 223-231. GONG Xiaonan. Plasticity of soil[M]. Hangzhou: Zhejiang University Press, 2001: 223-231. |
| [11] |
YIN J H, GRAHAM J. Viscous-elastic-plastic modelling of one-dimensional time-dependent behavior of clays[J]. Canadian Geotechnical Journal, 1989, 26: 199-209. DOI:10.1139/t89-029 |
| [12] |
胡亚元. n次齐次屈服函数相关联流动法则失效的机制研究[J]. 岩土工程学报, 2013, 35(2): 243-251. HU Yayuan. Failure mechanism of associated flow rule for n th homogenous yield function[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(2): 243-251. |
| [13] |
钱寿易, 符圣聪. 正常固结饱和黏土的孔隙水压力[J]. 岩土工程学报, 1988, 10(1): 1-7. QIAN Shouyi, FU Shengcong. Pore water pressure in normally consolidated saturated clays[J]. Chinese Journal of Geotechnical Engineering, 1988, 10(1): 1-7. |
| [14] |
拉特科斯基. 非线性回归模型-统一的实用方法[M]. 洪再吉等, 译. 南京: 南京大学出版社, 1986: 1-18. RATKOWSKY D A. Nonlinear regression modeling A unified practical approach[M]. HONG Zaijie, et al. translation. Nanjing: Press of Nanjing University, 1986: 1-18 |
| [15] |
张先伟. 结构性软土蠕变特性及扰动状态模型[D]. 长春: 吉林大学, 2010. ZHANG Xianwei. Creep characteristics of structured soft clay and its DSC model[D]. Changchun: Jilin University, 2010. |
 2018, Vol. 50
2018, Vol. 50


