2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
一直以来,单轴或者三轴试验是研究冻土力学特性的主要技术手段[1].然而,常规的三轴试验只能模拟冻土试样的轴对称应力状态(σ2=σ3),即为土体施加两个方向主应力下的力学行为,不能很好反映其在复杂应力路径下的强度与变形特征,无法考察大主应力方向和中主应力系数的影响[2].
目前,复杂应力路径下土体的力学特性研究主要针对未冻土开展,对于土体应力应变性状与强度影响的研究主要分为两个方面,分别是大主应力方向和中主应力系数.对于大主应力方向的变化,文献[3-10]分别用不同的试验土质,对原状或者重塑土样不同大主应力方向的应力-应变关系及各向异性属性进行了系统的研究.对于中主应力系数的影响,文献[11-12]分别对饱和砂土与粒状砂土进行了研究,发现中主应力系数会改变土样的力学行为.文献[13-14]研究了中主应力系数与强度参数和非共轴特性的依赖性.文献[15]利用真三轴发现中主应力系数的不同会引起土体强度的变化.
综上,大主应力方向和中主应力系数对未冻土的应力-应变关系曲线、强度以及各向异性特征都有显著的影响,然而关于冻土的相关研究还未见文献报道.为此利用冻土空心圆柱仪(FHCA-300)对饱和冻结黏土进行不同大主应力方向角和中主应力系数下的定向剪切试验.通过试验结果的对比分析,研究大主应力方向和中主应力系数对冻结黏土应力应变性状、强度以及各向异性的影响.
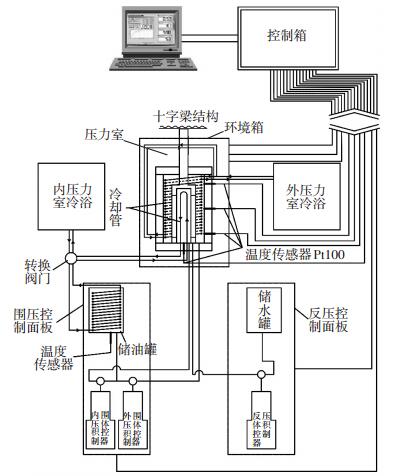
1 试验仪器、试样和方案 1.1 试验仪器及试样制备采用的仪器为中国科学院冻土工程国家重点实验室和美国GCTS公司联合研发的国内首台冻土空心圆柱仪(FHCA-300),可以模拟冻土在实际工程中的各种复杂应力路径,便于对冻土力学特性开展系统深入的研究.仪器结构如图 1所示,包括压力室及伺服主机系统、液压伺服加载系统、数字控制系统以及温度控制系统4部分,试验过程中可以独立施加和控制轴力W、扭矩MT、内围压pi、外围压po以及温度T[16].
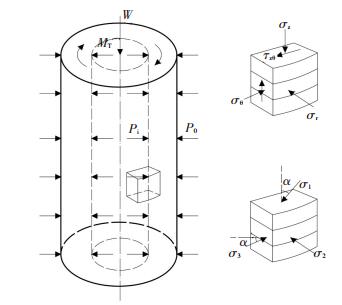
通过对空心圆柱试样施加独立控制的轴力、扭矩以及内、外围压,从而可以控制土体单元上3个主应力的大小以及大主应力方向.图 2为空心圆柱试样的受力状态.在试验过程中应力路径则是通过数学上的映射关系把加载的应力参数换算成平均主应力p、剪应力q、中主应力系数b以及大主应力方向角α来实现.其中,中主应力系数b和大主应力方向角α的计算见式(1)~(2).
|
图 2 空心圆柱仪试样的受力状态 Figure 2 Loading and stress states in hollow cylinder specimen |
中主应力系数b为
| $ b = \frac{{{\sigma _2}-{\sigma _3}}}{{{\sigma _1}-{\sigma _3}}} = \frac{{{\sigma _{\text{r}}}-\left( {{\sigma _{\text{z}}} + {\sigma _{\mathtt{θ}}}} \right)/2 + \sqrt {{{\left( {{\sigma _{\text{z}}} - {\sigma _{\mathtt{θ}}}} \right)}^2}/4 + \tau _{{\mathrm{z\mathtt{θ} }}}^2} }}{{2\sqrt {{{\left( {{\sigma _{\text{z}}} - {\sigma _{ \mathtt{θ}}}} \right)}^2}/4 + \tau _{{\mathrm{z\mathtt{θ} }}}^2} }}, $ | (1) |
大主应力方向角α为
| $ \alpha = \frac{1}{2}\arctan \frac{{2{\tau _{{\mathrm{z\mathtt{θ} }}}}}}{{{\sigma _{\text{z}}}-{\sigma _{\mathtt{θ}}}}}. $ | (2) |
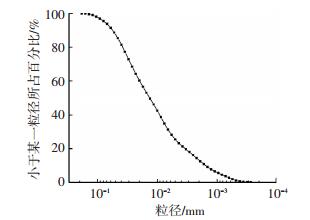
试验土样为青藏铁路沿线粉质黏土,颗粒级配见图 3,相关物理参数见表 1.土样从野外采集取回实验室,先自然风干后碾碎,再按照19.8%的含水量称取相应干土和蒸馏水进行配置,随后放入密封袋中静制24 h.根据试样压实体积和密度称取土样,分层均匀装入自制钢筒中并利用压样机变速率两头压实法制备,最终制成试样尺寸为200 mm×100 mm×60 mm(高×外直径×内直径)的空心圆柱试样,见图 4.将制备完成的试样快速装入压力室,启动制冷循环系统,将试样在-30 ℃下迅速冻结48 h,随后调节至目标温度,直到试样内外温度均达到设定值,且温度波动的范围小于±0.1 ℃,然后恒温12 h后即可开展试验,整个试验过程中温度保持恒定.
|
图 3 颗粒级配曲线 Figure 3 Grain size distribution curve of clay |
| 表 1 试验土样的物理参数 Table 1 Physical parameters of test soils |

|
图 4 空心圆柱试样 Figure 4 Hollow cylinder specimen |
为考察大主应力方向和中主应力系数对冻结黏土变形及强度的影响,开展了3组定向剪切试验,方案见表 2.整个试验过程分为两个阶段,第一阶段为初始阶段,即将所有的应力参数加载到初始设定值;第二阶段为加载阶段,即保持大主应力方向角α、中主应力系数b和平均主应力p不变,单纯增加剪应力q直至试样破坏,试验采用应力控制方式进行加载,剪切速率为30 kPa/min.
| 表 2 试验方案 Table 2 Test schemes |
空心圆柱试样的单元体在定向剪切应力路径下会产生轴向应变εz、扭剪应变γzθ、径向应变εr以及切向应变εθ,因此在变形分析过程中引入广义剪应变[17]来进行描述,见式(3)~(4).
广义剪应力
| $ {q_{\text{J}}} = \frac{1}{{\sqrt 2 }}\sqrt {{{\left( {{\sigma _1}-{\sigma _2}} \right)}^2} + {{\left( {{\sigma _2}-{\sigma _3}} \right)}^2} + {{\left( {{\sigma _3}-{\sigma _1}} \right)}^2}}, $ | (3) |
广义剪应变
| $ {\gamma _{\text{g}}} = \frac{{\sqrt 2 }}{3}{\left( {\frac{9}{2}\varepsilon _{\text{z}}^2 + \frac{3}{2}\gamma _{{\mathrm{z\mathtt{θ} }}}^2} \right)^{\frac{1}{2}}}, $ | (4) |
其中
式中:Δh为试样的轴向变形,mm;H0为试样的初始高度,mm;Δθ为试样的扭转角度;ro、ri分别为试样的外径和内径,mm.
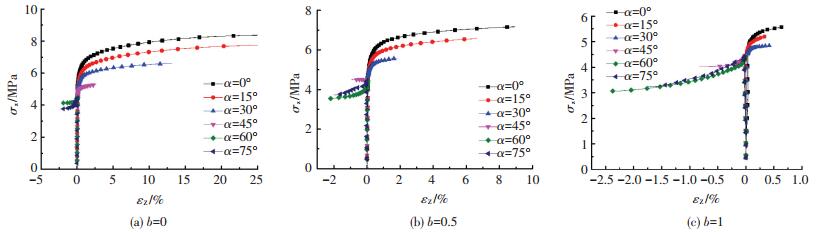
2.1 大主应力方向的影响由图 5可看出中主应力系数b为0、0.5、1.0时不同大主应力方向角α下的轴向应力-应变关系曲线各不相同.当大主应力方向角α为0°、15°以及30°时,轴向应力-应变曲线表现出明显的应变硬化特征,并随着大主应力方向角α的增加,轴向强度逐渐降低,试样发生压缩变形.而当大主应力方向角α为60°和75°时,轴向应变出现负值,且随着轴向应力的减小而持续发展,试样发生挤长变形.当大主应力方向角α为45°且中主应力系数b=0的情况时,试样被压缩,表现为应变硬化,但在中主应力系数b=0.5和b=1的情况时,轴向应变随着轴向应力的降低而逐渐减小,试样被拉伸.这是因为在大主应力方向角α=45°且中主应力系数b=0.5时,轴向力以及内外围压均在加载过程中保持不变,但随着扭矩逐渐增加,使得试样发生扭剪变形,由于试样的变形内围压会逐渐增大,轴向应力则会逐渐减小,同时试样整体被拉伸;而在大主应力方向角α=45°且中主应力系数b=1时,则是由于加载过程中轴向荷载逐渐降低,内外围压逐渐增加,导致试样被挤长,轴向应变呈现负值.
|
图 5 不同大主应力方向的轴向应力-轴向应变关系曲线 Figure 5 Axial stress-strain curves under different major principal stress directions |
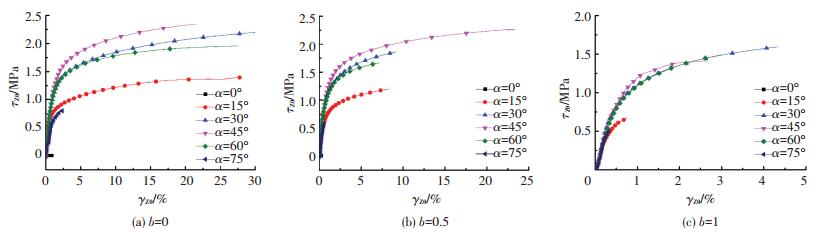
由图 6不同大主应力方向角α的扭剪分量应力-应变关系曲线可得,当大主应力方向角α=0°时,没有施加扭矩,因此中主应力系数b=0、0.5、1的试样均没有发生扭剪变形,扭剪应变始终为0.在3种不同中主应力系数b情况下,当大主应力方向角α小于45°时,冻结黏土的扭剪强度随着大主应力方向角α的增大而增大,而当大主应力方向角α大于45°时,扭剪强度则随着大主应力方向角α的增大而减小.由试验的6组大主应力方向角(α=0°、15°、30°、45°、60°以及75°)可以看出,当大主应力方向角α=45°时扭剪强度最大,而当大主应力方向角α=75°时扭剪强度最小.
|
图 6 不同大主应力方向的扭剪应力-扭剪应变关系曲线 Figure 6 Torsional stress-strain curves under different major principal stress directions |
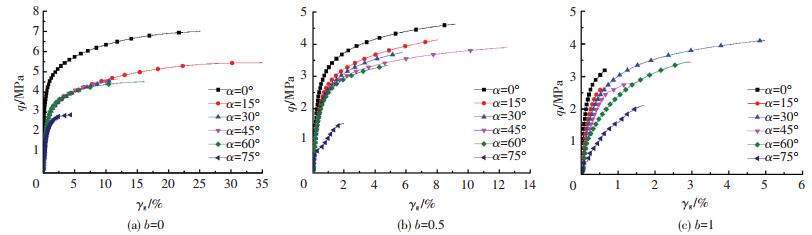
由图 7可得,不同大主应力方向角α下冻结黏土广义剪应力-剪应变关系曲线类型基本一致均为应变硬化型.整个加载过程可以分为两个阶段.在初始阶段(线性阶段),不同大主应力方向角α的广义剪应力-应变曲线陡直,斜率值较为接近且无明显变化,初始剪切模量基本相同,随着广义剪应力的增加广义剪应变的变化较小,整个第一阶段应变增加量不到1%.随着广义剪应力的持续增加,曲线出现拐点,随即进入第二阶段(非线性硬化阶段).此阶段随着广义剪应力的增加试样应变持续发展.由图 7中不同大主应力方向角α的试验结果分析可知,大主应力方向对广义剪应力-剪应变关系以及强度特性影响显著,随着大主应力方向角α的增加(大主应力方向角向横截面方向偏转),强度逐渐降低,这是由于受荷变形过程中剪切分量既界定偏转角的大小(保证应力路径),又主导土样整体的变形破坏特征.大主应力方向角α为15°、30°、45°以及60°时,不同中主应力系数b在同等广义剪应变下强度各不相同.当中主应力系数b=0且大主应力方向角α在15°~60°时,广义剪应力-剪应变曲线大致重合.当中主应力系数b为0.5和1时,大主应力方向角α在15°~60°之间的土样曲线硬化特征表现出不可忽略的方向依赖性,且随着大主应力方向角α的增大,曲线水平逐渐降低.
|
图 7 不同大主应力方向的广义剪应力-剪应变关系曲线 Figure 7 Generalized shear stress-strain curves under different major principal stress directions |
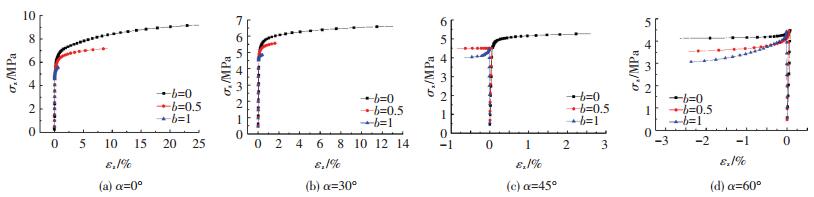
图 8显示,大主应力方向角α=0°、30°、45°、60°时不同中主应力系数b的轴向应力-应变关系曲线.可以看出,大主应力方向角α不同时,中主应力系数b对冻结黏土变形以及强度的影响也不同,表明土体的各向异性特征由初始组构异性特征和应力路径诱发各向异性特征共同决定,且后者占有主导作用[18].当大主应力方向角α=0°和α=30°时,不同中主应力系数b的轴向应力-应变曲线依然呈现应变硬化特征,且随着中主应力系数b的增加,轴向强度逐渐减小.当大主应力方向角α=45°、中主应力系数b=0时,轴向应变随着轴向应力的增加逐渐增大.但在大主应力方向角α=45°且中主应力系数b=0.5和b=1时,随着轴向应力的减小轴向应变呈现逐渐递减的趋势,即随着中主应力系数b从0增加到1,受到中主应力系数b的影响,试样从压缩状态变为拉伸状态.当大主应力方向角α=60°时,轴向应变都出现负值,试样均被拉伸,并随着中主应力系数b的增加,轴向强度逐渐降低.
|
图 8 不同中主应力系数下轴向应力-轴向应变关系曲线 Figure 8 Axial stress-strain curves under different coefficients of intermediate principal stress |
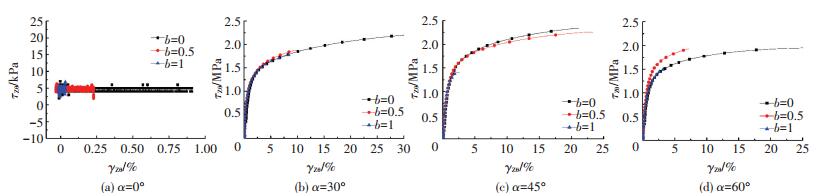
图 9为不同中主应力系数b扭剪分量的应力-应变关系曲线.在大主应力方向角α=0°时,加载过程中没有施加扭矩,因此如图 9(a)所示扭剪变形差异不是很大,均在很小的范围内波动.当大主应力方向角α<60°时(α<60°,图 9(a)~9(c)),不同中主应力系数b下的扭剪方向应力-应变曲线之间的差异不显著,曲线走势总体相似,其影响不明显;而当大主应力方向角α≥60°时(α≥60°,图 9(d)),中主应力系数b=0.5时曲线的强度略高于其他两个条件下的对应值,此时中主应力系数b的影响不可忽视.
|
图 9 不同中主应力系数下扭剪应力-扭剪应变关系曲线 Figure 9 Torsional stress-strain curves under different coefficients of intermediate principal stress |
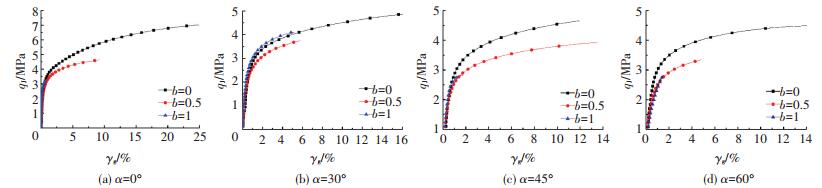
由图 10可知在不同中主应力系数b下,冻结黏土的广义剪应力-剪应变曲线特征基本相同,曲线水平及其发展特征基本一致.中主应力系数b=0.5和b=1的广义剪应力-剪应变曲线较为接近,相同的广义剪应变条件下,施加在试样上的广义剪应力水平基本相同,且强度低于中主应力系数b=0条件下的对应强度值.当中主应力系数b=0时,所有在大主应力方向角α条件下的广义剪应力-剪应变曲线水平基本高于其他中主应力系数b条件下的曲线水平.
|
图 10 不同中主应力系数下广义剪应力-广义剪应变关系曲线 Figure 10 Generalized shear stress-strain curves under different coefficients of intermediate principal stress |
1) 定向剪切路径下饱和冻结黏土应力-应变曲线基本呈现出应变硬化特征;在加载初期不同的大主应力方向角α和中主应力系数b下的初始剪切模量基本相同,随着剪应力的增加,冻结黏土的剪切模量则随着大主应力方向角α和中主应力系数b的增加而减小.广义剪应力-剪应变曲线受扭剪分量的主导.
2) 不同大主应力方向下冻结黏土应力-应变曲线水平存在一定差异,当中主应力系数b为0.5和1时广义剪应力-应变曲线水平随着大主应力方向角α的增加而降低.
3) 中主应力系数对冻结黏土扭剪分量应力应变性状影响相对较小,而对轴向分量与广义剪应力应变性状影响显著.
| [1] |
马巍, 王大雁. 冻土力学[M]. 北京: 科学出版社, 2014. MA Wei, WANG Dayan. Mechanics of frozen soil[M]. Beijing: Science Press, 2014. |
| [2] |
李广信. 高等土力学[M]. 北京: 清华大学出版社, 2005. LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University press, 2005. |
| [3] |
LADE P V, KIRKGARD M M. Effects of stress rotation and changes of b-values on cross-anisotropic behavior of natural, K0-consolidated soft clay[J]. Soils and Foundations, 2000, 40(6): 93-105. DOI:10.3208/sandf.4.6_93 |
| [4] |
LADE P V, NAM J, HONG W P. Shear banding and cross-anisotropic behavior observed in laboratory sand tests with stress rotation[J]. Canadian Geotechnical Journal, 2008, 45(1): 74-84. DOI:10.1139/T07-078 |
| [5] |
NAKATA Y, HYODO M, MURATA H H, et al. Flow deformation of sands subjected to principal stress rotation[J]. Soils and Foundations, 1998, 38(2): 115-128. DOI:10.3208/sandf.38.2_115 |
| [6] |
YOSHIMINE M, ISHIHARA K, VARGAS W. Effects of principal stress direction and intermediate principal stress on undrained shear behavior of sand[J]. Soils and Foundations, 1998, 38(3): 179-188. DOI:10.3208/sandf.38.3_179 |
| [7] |
KUMRUZZAMAN M D, YIN J H. Influences of principal stress direction and intermediate principal stress on the stress-strain-strength behaviour of completely decomposed granite[J]. Canadian Geotechnical Journal, 2010, 47(2): 164-179. DOI:10.1139/T09-0798 |
| [8] |
周建, 严佳佳, 刘正义. 原生和次生各向异性对软黏土强度和变形特性影响研究[J]. 岩土工程学报, 2013, 35(增刊2): 666-670. ZHOU Jian, YAN Jiajia, LIU Zhengyi. Effects of inherent and induced anisotropies on strength and deformation characteristics of soft clay[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(s2): 666-670. |
| [9] |
管林波, 周建, 张勋, 等. 中主应力系数和主应力方向对原状黏土各向异性的影响研究[J]. 岩石力学与工程学报, 2010, 29(增刊2): 3871-3877. GUAN Linbo, ZHOU Jian, ZHANG Xun, et al. Study of influence of parameters of intermediate principal stress and principal stress direction on anisotropy of intact clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(s2): 3871-3877. |
| [10] |
沈扬. 考虑主应力方向变化的原状软黏土试验研究[D]. 杭州: 浙江大学, 2007. SHEN Yang. Experimental study on effect of variation of principal stress orientation on undisturbed soft clay[D]. Hangzhou: Zhejiang University, 2007. |
| [11] |
YANG Z X, LI X S, YANG J. Undrained anisotropy and rotational shear in granular soil[J]. Géotechnique, 2007, 57(4): 371-384. DOI:10.1680/geot.2007.57.4.371 |
| [12] |
KANDASAMI R K, MURTHY T G. Experimental studies on the influence of intermediate principal stress and inclination on the mechanical behavior of angular sands[J]. Granular Matter, 2015, 17(2): 217-230. DOI:10.1007/s10035-015-0554-4 |
| [13] |
许成顺, 栾茂田, 何杨, 等. 中主应力对饱和松砂不排水单调剪切特性的影响[J]. 岩土力学, 2006, 27(5): 689-693. XU Chengshun, LUAN Maotian, HE Yang, et al. Effect of intermediate principal stress on undrained behavior of saturated loose sands under monotonic shearing[J]. Rock and Soil Mechanics, 2006, 27(5): 689-693. DOI:10.3969/j.issn.1000-7598.2006.05.002 |
| [14] |
杨彦豪, 周建, 温晓贵, 等. 杭州软黏土非共轴特性的试验研究[J]. 岩土力学, 2014, 35(10): 2861-2867. YANG Yanhao, ZHOU Jian, WEN Xiaogui, et al. Experimental study of non-coaxiality of Hangzhou soft clay[J]. Rock and Soil Mechanics, 2014, 35(10): 2861-2867. DOI:10.3321/j.issn:1000-7598.2014.10.2861 |
| [15] |
施维成, 朱俊高, 刘汉龙. 中主应力对砾石料变形和强度的影响[J]. 岩土工程学报, 2008, 30(10): 1449-1453. SHI Weicheng, ZHU Jungao, LIU Hanlong. Influence of intermediate principal stress on deformation and strength of gravel[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1449-1453. DOI:10.3321/j.issn:1000-4548.2008.10.005 |
| [16] |
郭妍, 王大雁, 马巍, 等. 冻土空心圆柱仪的研发与应用[J]. 哈尔滨工业大学学报, 2016, 48(12): 114-120. GUO Yan, WANG Dayan, MA Wei, et al. Development and application of frozen hollow cylinder apparatus[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 114-120. DOI:10.11918/j.issn.0367-6234.2016.12.016 |
| [17] |
沈瑞福, 王洪瑾, 周景星. 动主应力轴连续旋转下砂土的动强度[J]. 水利学报, 1996(1): 27-33. SHEN Ruifu, WANG Hongjin, ZHOU Jingxing. Dynamic strength of sand under cyclic rotation of principal stress directions[J]. Journal of Hydraulic Engineering, 1996(1): 27-33. |
| [18] |
王洪瑾, 张国平. 固有和诱发各向异性对击实粘性土强度和变形特性的影响[J]. 岩土工程学报, 1996, 18(3): 1-10. WANG Hongjing, ZHANG Guoping. Effects of inherent and induced anisotropy on strength and deformation characteristics of compacted cohesive soil[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(3): 1-10. DOI:10.3321/j.issn:1000-4548.1996.03.001 |
 2018, Vol. 50
2018, Vol. 50