2. 中国科学院大学,北京 100049;
3. 内蒙古大学 交通学院,呼和浩特 010070
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Transportation, Inner Mongolia University, Hohhot 010070, China
在多年冻土区和季节性冻土区进行工业与民用建筑、交通运输工程的建设,以及在人工冻土工程中冻结壁的设计和应用等,都会涉及冻土的强度问题.冻土作为一种特殊的岩土材料,其土颗粒的矿物成分、形状与级配等是影响强度的主要因素,含水量、加载速率及温度等外部条件的变化也会对冻土的强度产生影响[1-2].针对这些因素,国内外已开展了大量的试验研究来分析冻土的拉压强度特性,并给出相应的强度特征方程[3-7].在模型方程研究中,Zhu等[8]将冻土的应力-应变类型分为9种,分别给出相应的应力-应变方程;陈湘生[9]基于温度对冻土强度的影响提出冻土的瞬时强度模型,但此模型不能涵盖围压的影响,为此Fish[10]和马巍等[6]建议采用广义Drucker-Prager准则;王大雁等[11]利用Duncan-Chang双曲线模型分析了深部人工冻土的应力-应变行为;赖远明等[12]提出改进Duncan-Chang模型来分析冻土的应变软化现象和应变硬化现象.
以上研究大多数是在单轴压缩或三轴压缩等简单应力路径下冻土强度的试验研究成果,而开展主应力轴方向变化等复杂应力路径的试验主要在非冻土的强度特性研究中,发现土体的强度随a角的增大呈勺形变化,其最小值在a为60°左右[13-14];随着b值的增加不排水剪切强度均逐渐降低[15],应力-应变刚度呈现各向异性弱化效应,b值越大刚度弱化越显著[16];p值的改变会在试样中产生明显的剪切变形[17].由于试验仪器方面的限制,现有冻土力学的研究成果均未考虑主应力轴方向变化等对冻土强度的影响.随着冻土区工程的不断发展,对于工程中普遍存在的主应力轴方向变化等复杂应力状态,急需在室内试验中开展相关研究工作,为冻土区工程建设提供理论指导.为此,本文借助冻土空心圆柱仪,对重塑冻结黏土开展一系列主应力轴方向固定的定向剪切试验,探讨a角、b及p值的变化对冻结黏土强度特性的影响.
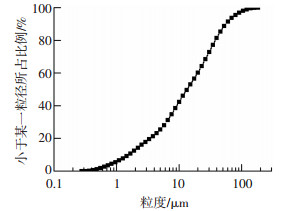
1 试样制备及试验设计 1.1 试样制备试验用土采自青藏公路沿线,为青藏粉质黏土,其基本的物理性质如表 1所示,颗粒级配见图 1.制样前,将土体在自然条件下风干碾碎过2 mm筛后密封保存.
|
图 1 土体的颗粒级配曲线 Figure 1 Grain-size distribution curve |
| 表 1 试验土的物理性质指标 Table 1 Basic physical properties of experiment soil |
为确定试样的饱和含水率,首先对试验用土进行标准实心试样(直径61.8 mm,样高125 mm)的抽气饱水试验,测定该饱和试样的干密度为1.77 g/cm3,含水率为19.8%.然后以此为标准推算所需的干土质量和制备饱和试样所需的水量.将一定量蒸馏水加入试验土并拌和均匀后过5 mm筛,在密封容器中静置24 h,使土中水均匀分布.通过自主研发的空心圆柱试样制样设备,将其制成干密度1.77 g/cm3、含水率19.8%的空心圆柱试样,试样的尺寸:高度h0=200 mm、外径d0=100 mm、内径di=60 mm、壁厚d=20 mm,见图 2.制备好的试样快速装入冻土空心圆柱试验机中,在-30 ℃条件下冻结48 h,再将温度调至试验温度,稳定24 h,使压力罐内温度均匀.

|
图 2 空心圆柱试样 Figure 2 Hollow cylinder specimen |
试验采用冻土工程国家重点实验室与美国GCTS公司联合开发的冻土空心圆柱仪(FHCA - 300),见图 3.该仪器能够独立控制和施加4个加载参数:轴力W、扭矩MT、内围压pi和外围压p0,从而控制3个主应力的大小和方向,能够更为真实的模拟冻土在主应力轴方向旋转等复杂应力路径下的应力-应变行为,其详细的仪器性能介绍见文献[18].

|
图 3 冻土空心圆柱试验机 Figure 3 Frozen soil hollow cylinder apparatus |
本次试验应力路径为定向剪切,设定应力路径时采用a、b、p及q(大小主应力值差的半值)4个参数,借鉴Hight等[13]提出的空心圆柱试样的计算公式,建立试验机加载参数与应力路径设定参数之间的映射关系:
| $ \begin{array}{l} W = \frac{q}{2}{\rm{ \mathit{ π} (}}1- 2b + 3{\rm{cos}}2\alpha ){\rm{ }}\cdot{\rm{ (}}{r_0}^2- {r_{\rm{i}}}^2) + {p_0}s, {\rm{ }}\\ {p_0} = \frac{{{r_{\rm{o}}}\left[{2p-\frac{q}{3}{\rm{(}}1-2b{\rm{)}}-q{\rm{cos}}2\alpha } \right] + q{r_{\rm{i}}}(2b - 1 + {\rm{cos}}2\alpha )}}{{2{r_{\rm{o}}}}}, {\rm{ }}\\ {p_{\rm{i}}} = \frac{{{r_{\rm{i}}}\left[{2p-\frac{q}{3}(1-2b{\rm{)}}-q{\rm{cos}}2\alpha } \right] + q{r_0}(2b -1 + {\rm{cos}}2\alpha )}}{{2{r_{\rm{i}}}}}, \\ {\rm{ }}{M_{\rm{T}}} = \frac{{\rm{ \mathit{ π} }}}{{{r_0} + {r_{\rm{i}}}}}q{\rm{sin}}2\alpha {\rm{(}}{r_0}^4 -{r_{\rm{i}}}^4). \end{array} $ |
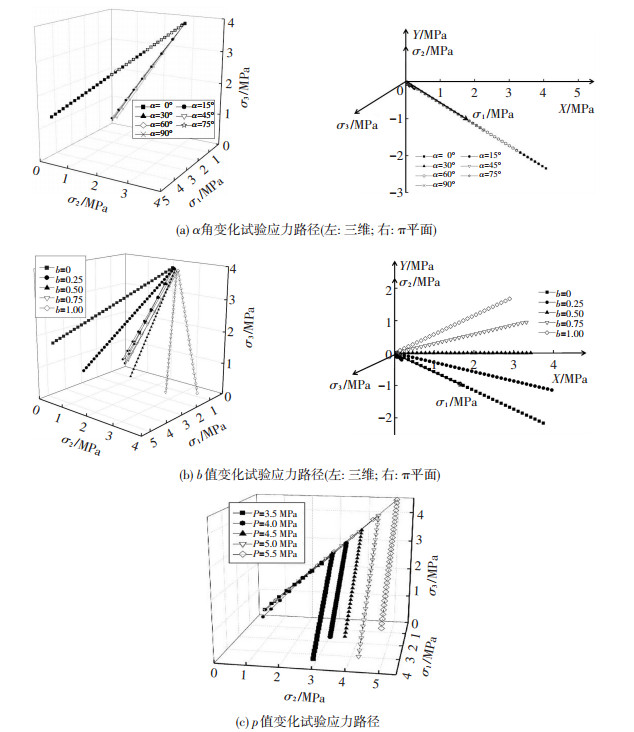
在-10 ℃条件下,开展3组试验:a角变化的试验(TA)、b值变化的试验(TB)和p值变化的试验(TP).试验过程分为两个阶段:第一阶段,将所有参数加载到应力路径设定的初始值;第二阶段,从初始值开始,保持a角、b及p值不变,控制q值以30 kPa/min的速率加载,直至试样发生破坏,具体参数设置见表 2.试验加载应力路径在主应力空间中的变化形式见图 4(图中二维坐标图为加载路径在π平面上的投影).
|
图 4 主应力空间中试验应力路径 Figure 4 The stress path in principal stress space |
| 表 2 试验应力路径表 Table 2 The stress path in tests |
试验应力路径中当有扭矩时(a ≠0°或90°),设置剪应变达到30%停止试验,当无扭矩时(a =0°或90°),设置轴向应变达到25%时停止试验.考虑到在定向剪切试验过程中,存在轴向力和扭矩的耦合加载,试样中各应变值的发展相互影响,因此采用广义剪应力qJ和广义剪应变γJ来分析冻结黏土的应力-应变行为.
广义剪应力
| $ {q_{\rm{J}}} = \frac{1}{{\sqrt 2 }}({({\sigma _1}-{\sigma _2})^2} + {{\rm{(}}{\sigma _1}-{\sigma _3})^2} + {{\rm{(}}{\sigma _2}-{\sigma _3})^2}){^{\frac{1}{2}}}, $ |
广义剪应变[19]:
| $ \begin{array}{l} {\gamma _{\rm{J}}} = \frac{{\sqrt 2 }}{3}\left( {\frac{9}{2}{\varepsilon _{\rm{a}}}^2 + \frac{3}{2}{\varepsilon _{\rm{s}}}^2} \right){^{\frac{1}{2}}}, \\ {\varepsilon _{\rm{a}}} = \frac{{{u_{\rm{a}}}}}{{{h_0}}}, {\varepsilon _{\rm{s}}} = \frac{{2\theta {\rm{(}}{r_0}^3-{r_{\rm{i}}}^3)}}{{3{H_0}({r_0}^2-{r_{\rm{i}}}^2)}}. \end{array} $ |
式中:εa为轴向应变,εs为剪应变,ua为轴向位移,θ为试样扭转角,εa和εs均为基于试样整体测量的试验结果.通过qJ-γJ曲线更能综合反映不同影响因素下冻结黏土中力学特性的变化规律.
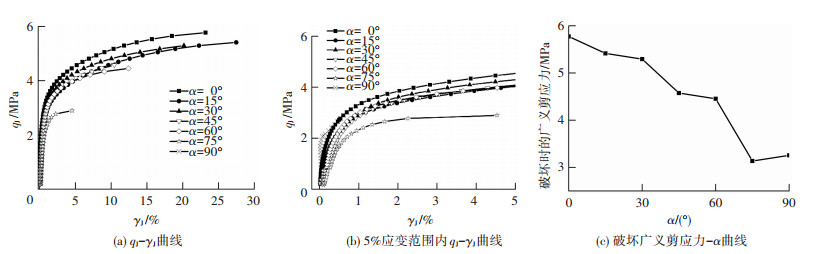
2.1 大主应力方向角a的影响大主应力方向角a表征大主应力σ1偏离竖直方向的程度.图 5为不同a角时试验结果曲线,其中图 5(b)为试样在应变值为0%~5%范围内的应力-应变特征曲线.从图 5(a)可得出不同a角下qJ-γJ曲线均呈双曲线型,且类似于弹性塑性应变硬化曲线,γJ随着qJ的增加而增加.初始加载阶段,应力-应变曲线近似呈线性变化,线性变化段的极限应变值在0.5%左右;随着变形的继续发展,应变增加的速率逐渐增大,破坏时的qJ值随着a角的增加先减小而后又出现增加的变化趋势,最小值出现在a=75°(图 5(c)).a=90°时的qJ-γJ曲线表现出随着广义剪应力的增加,应变先减小到0附近然后又开始逐渐增加,这主要是因为当a=90°时,大主应力σ1在水平方向,而与之垂直的小主应力σ3在竖直方向,试样处于拉伸应力状态,当第一阶段加载完成后,试样轴向变形为压缩变形,在第二阶段加载过程中轴向变形先减小到0然后再向拉应变方向发展,此应力路径中无扭矩,故广义剪应变在数值上等于轴向应变的绝对值,因此会出现该种现象.同时从图 5(b)也可以看出,a=0°和a=90°曲线在一定变形后趋于重合,但由于土体的抗拉强度远低于抗压强度,故在a=90°时,γJ发展到1%时试样发生破坏.
|
图 5 不同a角时试验结果曲线 Figure 5 Test result curves in different a angle stress paths |
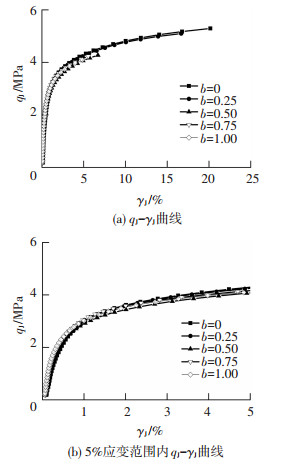
图 6为a=30°时不同b值下的qJ-γJ曲线.从图中可以看出,不同b值下的qJ-γJ曲线之间的差异很小,几乎是重合发展,破坏时的广义剪应力值随b值增加逐渐减小,破坏时的广义剪应变值也随b值的增加有较大幅度的减小.在初始加载阶段,不同b值之间的差值不是很明显,应力-应变曲线也近似为线性变化,极限应变值同样在0.5%左右.
|
图 6 不同b值时qJ-γJ曲线 Figure 6 qJ-γJ curves in different b stress paths |
平均主应力p值变化代表不同π平面上的应力路径,图 7为a=30°时不同p值应力路径下的qJ-γJ曲线.从图中可以看出,在初始加载阶段,应力-应变曲线近似为线性变化,极限应变值在0.5%左右,p值的变化对线性阶段的发展影响不大.当应变值超过0.5%后,相同γJ值对应的qJ先随p值的增加而增加,随后随着p值的继续增加,qJ值又开始逐渐减小.故在试验应力范围内,当大主应力方向角a=30°时,平均主应力p=5.0 MPa时,qJ值最大.产生这种现象是因为随着p值的增加,土体颗粒和冰逐渐被压密,增大了颗粒间的摩擦力,使土体的强度增加;随着p值的继续增大,部分冰被压融,使冻土中未冻水含量增加,减小了颗粒间的摩擦力,同时部分土颗粒也可能出现压碎的现象,使冻土土体结构发生破坏,致使冻土强度降低.
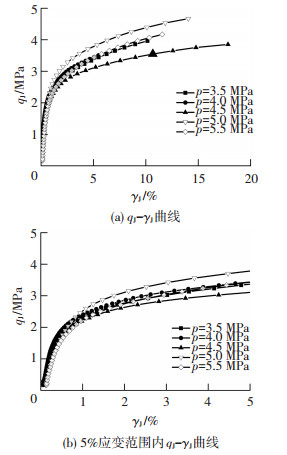
|
图 7 不同p值时qJ-γJ曲线 Figure 7 qJ-γJ curves in different p stress paths |
在定向剪切试验中,qJ-γJ曲线呈双曲线形发展.为探索冻结黏土的强度模型,分别绘制出不同应力路径下γJ/qJ-γJ曲线,如图 8所示,以γJ为横坐标,以γJ/qJ为纵坐标.从图中可以看出,γJ与γJ/qJ之间近似呈线性关系,因此二者之间的关系可用线性方程来表示:
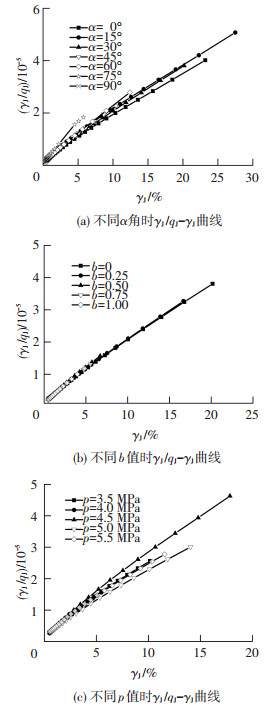
|
图 8 γJ/qJ-γJ曲线 Figure 8 γJ/qJ-γJ curves |
| $ \frac{{{\gamma _{\rm{J}}}}}{{{q_{\rm{J}}}}}{\rm{ = }}m + n{\gamma _{\rm{J}}}, $ | (1) |
式中m和n为与土质及应力路径有关的试验常数.试验数据经拟合后,可得出不同应力路径下的m和n值,且拟合度都达到0.99以上(见表 3).
| 表 3 不同应力路径下系数m和n的计算值 Table 3 Calculated values of m and n in different stress paths |
将式(1)整理,可得qJ-γJ的关系表达式为
| $ {q_{\rm{J}}} = \frac{{{\gamma _{\rm{J}}}}}{{m + n{\gamma _{\rm{J}}}}}, $ | (2) |
根据式(2)可求得广义剪切模量EJt的表达式为
| $ {E_{{\rm{Jt}}}} = \frac{{\partial {q_{\rm{J}}}}}{{\partial {\gamma _{\rm{J}}}}} = \frac{m}{{{{(m + n{\gamma _{\rm{J}}})}^2}}}, $ | (3) |
由式(3)可得,当γJ=0时,初始剪切模量EJt=1/m;当γJ→+∞时,由式(2)得极限广义剪应力值qJ|ult=1/n.因此m和n的物理意义为m为初始剪切模量的倒数,n为qJ-γJ曲线的渐近线所对应的广义剪应力值的倒数,这与Duncan-Chang[20]的双曲线模型中参数的物理意义相同.
由式(3)可以绘制出广义剪切模量随γJ的变化趋势图,如图 9所示.从图 9可得出,随着变形发展,广义剪切模量都呈递减趋势,应力路径变化对初始广义剪切模量EJt0的影响较大.随着a角的增大,EJt0先减小而后逐渐增大,增大到最大点后随着a角的继续增大然后降低,两个极值点分别为a=15°(最小点)和a=60°(最大点).EJt0随着b值增加而增大,随着p值增加,EJt0先增加而后减小.同时从图 9还可以得出,EJt0存在一个临界值E′Jt0,当EJt0 < E′Jt0,EJt-γJ曲线发展比较缓和,EJt0值越小,曲线越平缓,破坏时的γJ也较大;当EJt0>E′Jt0,EJt-γJ曲线逐渐变陡,EJt0值越大曲线斜率越大,破坏时的γJ越小,对于冻结黏土E′Jt0=6×105 kPa.
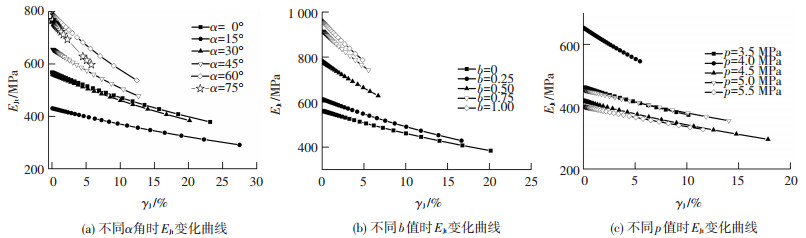
|
图 9 剪切模量EJt变化曲线 Figure 9 EJt curves in different stress paths |
1) 大主应力方向角a、中主应力系数b及平均主应力p值的变化都会对冻土的强度产生较大影响.随着a角的增加,破坏时的广义剪应力qJ值先增加后减小,最小值出现在a=75°处;b值变化对qJ值的影响较小,破坏时的广义剪应变γJ随b值的增加有较大幅度的减小;随着p值增加,相同γJ值对应的qJ值先增加后减小.
2) 冻结黏土的qJ-γJ曲线为弹性塑性应变硬化曲线.在初始加载阶段,应力-应变曲线呈线性变化,线性段极限应变值在0.5%左右,可以将该点作为冻土的初始屈服点.
3) γJ与γJ/qJ之间呈线性关系,采用Duncan-Chang双曲线模型方程作为冻结黏土定向剪切条件下的强度模型方程,试验常数m和n受a角、b值和p值变化影响较大.
4) a角、b值和p值变化对冻土的初始广义剪切模量EJt0有较大影响.EJt0存在一个临界值E′Jt0,当EJt < E′Jt0,EJt-γJ曲线发展比较缓和,EJt0值越小,曲线越平缓,破坏时的γJ也较大;当EJt0>E′Jt0,EJt-γJ曲线逐渐变陡,EJt0值越大曲线斜率越大,破坏时的γJ越小,对于冻结黏土E′Jt0=6×105 kPa.
| [1] |
马巍, 王大雁. 冻土力学[M]. 北京: 科学出版社, 2014. MA Wei, WANG Dayan. Mechanics of frozen soil[M]. Beijing: Science Press, 2014. |
| [2] |
王大雁, 马巍, 常小晓, 等. 深部人工冻土抗变形特性研究[J]. 岩土工程学报, 2005, 27(4): 418-421. WANG Dayan, MA Wei, CHANG Xiaoxiao, et al. Study on resistance to deformation of artificially frozen soil in deep alluvium[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(4): 418-421. DOI:10.3321/j.issn:1000-4548.2005.04.011 |
| [3] |
ALKIRE B D, ANDERSLAND O B. The effect of confining pressure on the mechanical properties of sand-ice materials[J]. Journal of Glaciology, 1973, 12(66): 469-481. DOI:10.1017/S0022143000031889 |
| [4] |
张锋, 林波, 冯德成, 等. 季节冻土区长期交通荷载下公路路基永久变形特性[J]. 哈尔滨工业大学学报, 2017, 49(3): 120-126. ZHANG Feng, LIN Bo, FENG Decheng, et al. Permanent deformation of subgrade induced by long-term truck traffic loading in seasonally frozen regions[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 120-126. DOI:10.11918/j.issn.0367-6234.2017.03.019 |
| [5] |
MA Wei, WU Ziwang, ZHANG Lixin, et al. Analyses of process on the strength decrease in frozen soils under high confining pressures[J]. Cold Regions Science and Technology, 1999, 29(1): 1-7. DOI:10.1016/S0165-232X(98)00020-2 |
| [6] |
马巍, 吴紫汪, 张长庆. 冻土的强度与屈服准则[J]. 冰川冻土, 1993, 15(1): 319-322. MA Wei, WU Ziwang, ZHANG Changqing. Strength and yield criterion of frozen soil[J]. Journal of Glaciology and Geocryology, 1993, 15(1): 319-322. |
| [7] |
吴紫汪, 马巍. 冻结砂土的强度特性[J]. 冰川冻土, 1994, 16(1): 15-20. WU Ziwang, MA Wei. Strength characteristics of frozen sandy soil[J]. Journal of Glaciology and Geocryology, 1994, 16(1): 15-20. |
| [8] |
ZHU Yuanlin, ZHANG Jiayi. Constitutive relations of frozen soil in uniaxial compression[C]//Proceeding of 6th Internet Conference on Permafrost. Beijing: [s. n. ], 1991: 1092-1095.
|
| [9] |
陈湘生. 人工冻土瞬时三轴剪切强度特征的试验研究[J]. 建井技术, 1992(6): 38-40. CHEN Xiangsheng. Experimental study on strength of artificially frozen soil under transient triaxial compression[J]. Mine Construction Technology, 1992(6): 38-40. DOI:10.19458/j.cnki.cn11-2456/td.1992.06.017 |
| [10] |
FISH A M. Strength of frozen soil under a combined stress state[C]//Proceedings of the 6th International Symposium on Ground Freezing. Beijing: [s. n. ], 1991: 135-145.
|
| [11] |
王大雁, 马巍, 常小晓. K0固结后卸载状态下冻土应力-应变特性研究[J]. 岩石力学与工程学报, 2004, 23(8): 1252-1256. WANG Dayan, MA Wei, CHANG Xiaoxiao. Study on behavior of stress-stain for frozen soils subjected to K0 consolidation by unloading triaxial shear tests[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(8): 1252-1256. DOI:10.3321/j.issn:1000-6915.2004.08.004 |
| [12] |
赖远明, 程红彬, 高志华, 等. 冻结砂土的应力-应变关系及非线性莫尔强度准则[J]. 岩石力学与工程学报, 2007, 26(8): 1612-1617. LAI Yuanming, CHENG Hongbin, GAO Zhihua, et al. Stress-strain relationships and nonlinear Mohr strength criterion of frozen sand clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1612-1617. DOI:10.3321/j.issn:1000-6915.2007.08.011 |
| [13] |
HIGHT D W, GENS A, SYMES M J. The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils[J]. Geotechnique, 1983, 33(4): 355-383. DOI:10.1680/geot.1983.33.4.355 |
| [14] |
姚兆明, 姜自华, 王春萌, 等. 恒定主应力偏转角下黏土不排水剪切特性分析[J]. 力学与实践, 2016, 38(1): 56-62. YAO Zhaoming, JIANG Zihua, WANG Chunmeng, et al. Characteristics of clay subjected to undrained shear with consideration of influence of deflection angle of principal stress axis[J]. Mechanics in Engineering, 2016, 38(1): 56-62. DOI:10.6052/1000-0879-15-104 |
| [15] |
柳艳华, 谢永利. 主应力轴旋转下中主应力系数对软黏土性状的影响[J]. 交通运输工程学报, 2015, 15(3): 27-33, 61. LIU Yanhua, XIE Yongli. Influence of intermediate principal stress coefficient on character of soft clay under rotation of principal stress axes[J]. Journal of Traffic and Transportation Engineering, 2015, 15(3): 27-33, 61. DOI:10.3969/j.issn.1671-1637.2015.03.005 |
| [16] |
钱建固, 杜子博. 纯主应力轴旋转下饱和软黏土的循环弱化及非共轴性[J]. 岩土工程学报, 2016, 38(8): 1381-1390. QIAN Jiangu, DU Zibo. Cyclic degradation and non-coaxiality of saturated soft clay subjected to pure rotation of principal stress axis[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1381-1390. DOI:10.11779/CJGE201608004 |
| [17] |
PRADEL D, ISHIHARA K, GUTIERREZ M. Yielding and flow of sand under principal stress axes rotation[J]. Soils & Foundations, 1990, 30(1): 87-99. DOI:10.3208/sandf1972.30.87 |
| [18] |
郭妍, 王大雁, 马巍, 等. 冻土空心圆柱仪的研发与应用[J]. 哈尔滨工业大学学报, 2016, 48(12): 114-120. GUO Yan, WANG Dayan, MA Wei, et al. Development and application of frozen hollow cylinder apparatus[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 114-120. DOI:10.11918/j.issn.0367-6234.2016.12.016 |
| [19] |
沈瑞福, 王洪瑾, 周景星. 动主应力轴连续旋转下砂土的动强度[J]. 水利学报, 1996(1): 27-33. SHEN Ruifu, WANG Hongjin, ZHOU Jingxing. Dynamic of sand under cyclic rotation of principal stress directions[J]. Journal of Hydraulic Engineering, 1996(1): 27-33. DOI:10.13243/j.cnki.slxb.1996.01.005 |
| [20] |
李广信. 高等土力学[M]. 北京: 清华大学出版社, 2005. LI Guangxin. Advanced soil mechanics[M]. Beijing: Tsinghua University Press, 2005. |
 2018, Vol. 50
2018, Vol. 50


