2. 岩土及地下工程教育部重点实验室(同济大学),上海 200092
2. Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China
粗粒土具有强度高、变形小、渗透性好等特性,广泛应用于坝体、路基等工程建设,近年来中国超高坝建设发展较快,对在髙应力下粗粒土力学和坝工特性的研究引起较多学者关注.
土体颗粒的破碎是指成岩土体的粗颗粒在外部因素作用下导致土体颗粒的结构发生碎裂,分裂成多个颗粒的现象[1].粗粒土的颗粒破碎可引起土体级配改变,导致土体本身结构发生改变,对土体的强度、内摩擦角、渗透系数等都会产生不可忽视的影响.
针对土体颗粒的破碎进行研究最早始于20世纪初,但受限于当时的试验条件,没有取得突出成果.1948年,现代土力学奠基人太沙基在砂土的压缩试验中发现颗粒破碎现象十分明显[2],随后,越来越多的研究人员开始了对颗粒破碎的研究[3-7].杨光等[8]采用大型三轴试验机,研究了粗粒料在不同应力路径下的颗粒破碎情况,分析了应力路径对颗粒破碎和强度特性的影响.王子寒[9]通过粒间接触力学试验、大型直剪试验以及离心模型试验,对粗粒土的粒间接触力学特性及细观接触模型进行了实际测试和模型验证,并提出了基于试验的接触力-变形拟合公式.Wang等[10]通过单轴压缩试验研究了砂土颗粒裂隙扩展和破碎过程,发现了破碎模式与颗粒强度之间的关系.Tejchman等[11]通过在有限元中引入局部破碎机制,模拟了粗粒料在恒定围压下的单向压缩试验,成功预测出了剪切带上土颗粒的破碎与变形特性.而离散元方法的兴起突破了细观机理研究中常规的室内土工试验的一些限制[12],为颗粒体系力学行为和颗粒破碎的研究开辟了新的方向.学者们利用DEM在研究颗粒接触力学问题上进行了诸多尝试[13].王强强[7]使用PFC3D对石膏颗粒接触试验进行了模拟,发现通过单轴压缩试验标定的数值参数并不适用于颗粒接触数值模型. Manouchehrian等[14]用离散元软件对存在不同裂隙走向的岩石样本进行模拟,研究了脆性材料在不同压力荷载下细观状态的裂隙发展趋势.过去对于粗粒料等散粒体的研究,主要是基于颗粒群概念,从平均应力角度针对颗粒集合体的物理力学性质展开研究,从颗粒接触的角度对颗粒破碎的过程、形态和机理进行的研究较少,试验数据无法直接得到颗粒破碎时与颗粒接触相关的物理力学参数,难以揭示单个颗粒的破碎过程与机理.
本文从颗粒接触的角度,利用岩石双轴流变试验机进行了大理岩球形颗粒接触的球-面接触试验和球-球接触试验,研究大理岩球形颗粒在点-面、点-点接触条件下的破碎形态及破碎机理.本文还利用PFC3D建立了大理岩颗粒接触试验的数值模型,引入带有强度折减参数的接触模型,模拟了大理岩球形颗粒接触加载和破碎的过程,得到的单颗粒破碎形态与试验结果相近.通过对接触局部破碎区发展的观察以及对数值模型基本颗粒位移的分析,为试验结果提供了良好的补充,进一步揭示了大理岩球形颗粒接触破碎过程的细观机理,也证明了强度折减参数在脆性材料颗粒接触研究中的适用性.
1 颗粒接触室内试验 1.1 试验设备与试验材料试验设备采用岩石双轴流变试验机,该仪器能够提供稳定的位移控制和伺服控制双轴加载条件.特别定制了合适尺寸的加载系统及球铰支座.测量与控制精度极高且实现了数字化操作,可实时采集、记录数据,颗粒受力与变形的量测精度分别为5 N和0.001 mm.加载部分如图 1所示.

|
图 1 接触试验装置 Figure 1 Experimental facilities for contact test |
考虑到现场粗粒土颗粒大小、形状和岩性材料均不同,难以进行重复性试验,作为机理初步研究,本文选用典型的大理石,统一加工粒径为5 cm的球形颗粒来研究粗粒土接触破碎问题.试验所用大理岩材料按标准试验实测的岩石基本力学参数如表 1所示.
| 表 1 大理岩基本力学参数 Table 1 Physical parameters of marble |
考虑到岩石材料本身较大的离散性,采用多次重复试验的方法来研究球形试样球-球接触和球-面接触条件下的破碎形态与破碎机理.
1.2 试验步骤及加载条件试验过程可分为试验前准备、装样、加载及数据采集等主要步骤.
1) 在设备启动之前先将辅助夹具进行润滑处理,在法向接触试验中所用球铰支座两个部件的接触面之间涂抹润滑油,以消除摩擦力对试验结果的影响.
2) 装样时先将球铰支座用弹簧连接到设备下部的法向加载臂上,然后将球颗粒的固定支座等尽量放置到球铰支座表面形心的位置上(由于球铰支座可以有效防止试样偏心,在对正时允许存在误差).在相应的刚性垫块或球颗粒固定支座上放置大理岩颗粒,并开启试验设备,将设备采集到的法向力置零.
为了确保加载臂与粗粒土颗粒或加载支座完全接触,通常要预施加200 N左右的法向力,然后将设备采集到的法向和切向位移置零(由于预荷载产生的位移较小,所以此时将位移置零产生的误差不会影响试验结果).
3) 试验过程中使用位移控制的加载方式,以观察破坏后接触力-位移关系的变化,球-面接触试验和球-球接触试验均采用0.002 mm/s的加载速率进行.球-面接触条件下加载位移为1 mm,因为球-球接触条件下加载位移太大会使试样从加载平台掉落,所以加载位移设为0.7 mm.所有试验数据采集频率为1 Hz.
需要说明的是,对于岩石的标准试样,国际岩石力学学会建议方法及中国水利规程要求按照0.5 MPa/s的应力速率加载.但对于颗粒之间的接触试验并没有统一的标准.课题组前期研究中是以接触力5 N/s来进行加载,当试样破坏时,由于突然卸载引起的瞬时位移会激发系统的保护限制而导致加载停止,无法测得试样破坏后的接触力-位移曲线.因此本文采用位移控制进行加载.但位移控制的方法并没有统一的试验标准,一般认为应变速率低于10 -4s-1属于低应变速率;10-4~102 s-1属于中等应变速率,其中10-4~10-2 s-1属于准静态,10-2~102 s-1属于准动态;>102 s-1属于动态加载[15].虽然接触试验中并没有应变的概念,但作为对照,将加载速率除以试样的直径,可以得到试验的加载过程属于静态或准静态过程.
1.3 球-面接触试验破碎形态为探究大理岩颗粒球-面接触的破碎形态,一共进行了40组有效的球-面接触试验.
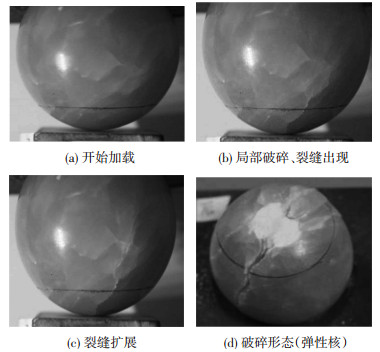
40组试验颗粒的破碎过程相似.首先,颗粒与平面接触点处由于应力集中而产生局部破碎,试验发现,局部破碎区域会逐渐形成近似圆形的平台,周围有碎屑产生.随着加载的进行,在颗粒的接触平台下形成一个锥形体,本文暂称其为弹性核[16],在弹性核附近开始产生若干裂缝并发展,裂缝贯通后颗粒整体破碎成2~4块, 如图 2所示.
|
图 2 直径5 cm大理岩球形颗粒球-面接触破碎过程 Figure 2 5 cm marble breakage process under ball-surface contact condition |
图 3所示为球-面接触整体破碎后的形态,其中(b)为弹性核的剖面放大图.可以发现,颗粒在接触处形成了一个近似圆形的平台,平台下有一个弹性核,在弹性核附近形成了3条裂缝,裂缝发展方向与接触面垂直,将颗粒分成了3块.

|
图 3 大理岩球形颗粒球-面接触破碎形态 Figure 3 Marble particle breakage morphology under ball-surface contact condition |
本小节通过球-球接触试验研究了大理岩球形颗粒接触破碎的形态,共进行了20组有效试验,每一组试验的破碎过程相似.
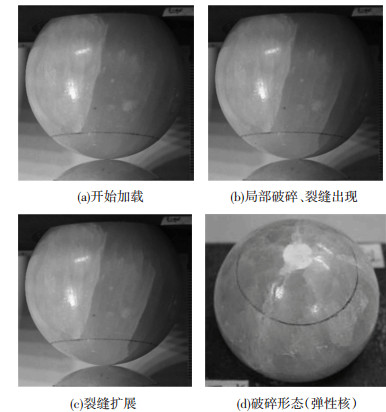
球-球颗粒接触破碎过程如图 4所示,与球-面接触类似,在两个球形颗粒接触处存在应力集中现象,颗粒首先发生局部破碎.随着加载的进行逐渐形成锥形体弹性核,在弹性核附近产生裂缝并发展,裂缝贯通后颗粒整体破碎.球-球接触试验中均为一侧颗粒发生破碎,另一侧的颗粒基本不变,但也有个别颗粒在接触点处出现了微小的白色痕迹,局部形状没有发生变化且球面依然光滑.
|
图 4 直径5 cm大理岩球形颗粒球-球接触破碎过程 Figure 4 5 cm marble breakage process under ball-ball contact condition |
图 5所示为球-球接触整体破碎后的形态,其中(b)为弹性核的剖面放大图.破碎的大理岩颗粒可被观察到弹性核以及一条贯穿的主裂缝,将球形颗粒分成了质量几乎相等的两块.

|
图 5 大理岩球形颗粒球-球接触破碎形态 Figure 5 Marble particle breakage morphology under ball-ball contact condition |
试验中接触力-位移曲线由双轴流变试验机的量测系统测得,位移为前后两个位移计记录结果的平均值,接触力通过轴向加载装置的测力系统获得.
1.5.1 球-面接触试验试验中大理岩球形颗粒的力-位移曲线如图 6所示,每张图 5组试验曲线.在试验加载开始时,当加载力达到一定值,大理岩球形颗粒接触点首先发生局部破碎,曲线的第一个上升段为颗粒局部破碎和弹性核产生并发展阶段.第一个上升段的顶点为颗粒局部破碎和整体破碎的分界点,之后为颗粒整体破碎后的加载阶段.

|
图 6 球-面接触试验力-位移曲线 Figure 6 Force-displacement curve under ball-surface contact condition |
根据试验统计结果,球-面接触形式下,大理岩颗粒发生整体破碎时的法向接触力范围为2.500~ 8.000 kN,平均值为5.156 kN,第一阶段平均斜率为26.559 kN/mm.发生颗粒整体破碎之后,由于颗粒破碎峰后强度及曲线斜率与破碎后的受力状态有关,而破碎块体数、贯通裂缝宽度等的不确定性,使得破碎后试样的受力状态具有很大随机性,表现为图中的峰后曲线离散性极大,颗粒的二次破碎没有得到明确的统计规律.
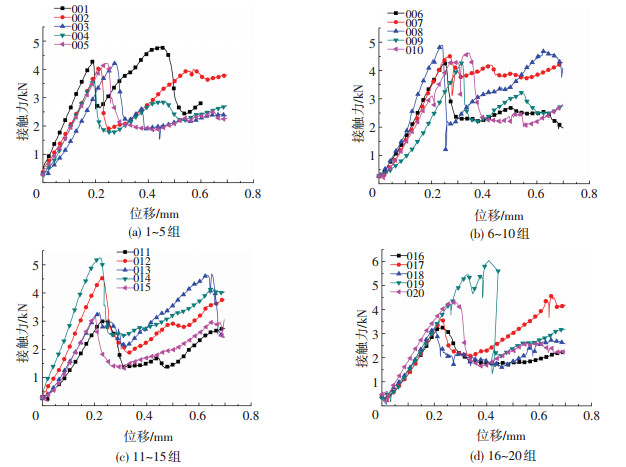
1.5.2 球-球接触试验试验中大理岩球形颗粒的力-位移曲线如图 7所示,与球-面接触类似,大理岩颗粒在加载过程中经历了局部破碎与整体破碎两个阶段,曲线的第一个转折点即两个阶段的分界点.
|
图 7 球-球接触试验力-位移曲线 Figure 7 Force-displacement curve under ball-ball contact condition |
根据试验统计结果,球-球接触形式下,大理岩颗粒发生整体破碎时的法向接触力范围为3.002~ 5.500 kN,平均值为4.001 kN,第一阶段平均斜率为16.885 kN/mm.
2 颗粒接触试验的数值模拟本文采用离散元软件PFC3D进行数值模拟.由于该软件所用的方法假定单个基本颗粒为刚性体,无法产生变形和破碎,而岩石颗粒材料在受力过程中自身会发生一定的变形并发生开裂和破碎,因此不能用单个基本颗粒来模拟大理石球形颗粒.故本文采用一群大小不一的小颗粒来模拟大理石试样.
为了使构建的数值模型能够模拟试验中表现出的宏观现象,必须建立模型的宏观力学特性与一系列细观参数之间的联系.由于两者之间没有直接的数学关系,需要通过反复计算,结合标定与交互调试才能将多组参数同时匹配成功,得到与试验相似的结果.
2.1 数值模型的选择为了便于测量球形颗粒对墙体的反力和观察接触力的变化,并考虑到对称性,使用半球模型来模拟大理石球形颗粒,数值模型的形状和尺寸与试验的大理石球形颗粒一致.半球形模型的直径为50 mm,具体颗粒数量与粒径根据实际情况调整.采用PFC3D程序中的墙(wall)单元模拟接触面,同样使用墙单元来加载.
在前期使用PFC3D内置的平行黏结模型试算时发现,半球面模型的破碎区域集中在接触点的附近,无法向下发展成整体破碎.为此,本文在平行黏结模型中引入一个强度折减参数,在模拟过程中实时降低发生黏结断裂颗粒周围区域颗粒的黏结强度,来模拟应力集中和局部破碎导致的局部强度降低,该参数对数值模拟结果的影响主要体现在最终破碎形态上.通过试算发现,强度折减影响的范围与数值颗粒的粒径分布有关,需要根据具体数值参数确定.
为了直观显示破碎区域,利用PFC3D自带的FISH语言编写了一个子程序,将模拟过程中所有发生黏结断裂的颗粒改为红色.若观察到红色连接成面,则说明试样产生了贯通裂缝.
数值模拟需要标定以下5组数值参数:
1) 接触模量Ec和平行黏结模量Ec;
2) 颗粒法向刚度与切向刚度的比值kn/ks;
3) 平行黏结法向刚度与切向刚度的比值kn/ks;
4) 平行黏结的法向和切向强度平均值(σc、τc)及破碎位置周围降低的强度值;
5) 生成试样时的各向同性应力.
根据课题组的数值参数调试经验[7, 9, 17],以上第1)组参数主要影响颗粒接触的力-位移曲线的斜率,第4)组参数主要影响破碎强度,而第5)组参数主要影响整体破碎程度.具体数值参数由对颗粒破碎试验的标定与试算获得.
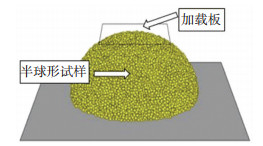
2.2 球-面接触试验的数值模拟 2.2.1 数值参数的确定半球形模型由大小不一的基本颗粒组合而成,如图 8所示.为了平衡计算精度与效率,基本颗粒最小粒径取为1.5 mm,最大粒径与最小粒径的比值取为1.8,颗粒总数约30 000个.
|
图 8 球-面接触试验数值模型 Figure 8 Numerical model of ball-surface contact test |
当取颗粒的最小粒径为1.5 mm,最大粒径与最小粒径的比值为1.8,粒径总体呈正态分布时,其强度折减影响的范围为发生黏结断裂的两个基本颗粒球半径之和的1.5倍.
课题组前期模拟及试算表明,由于存在明显的应力集中现象,通过单轴压缩试验标定的细观模量与强度参数不能直接用于接触试验模拟,因此首先建立接触试验数值模型,然后在不进行强度折减情况下进行细观参数标定,过程如下:首先标定接触模量Ec和平行黏结模量Ec,标定目标值依据为接触试验割线模量(统计均值).将材料强度固定为60 MPa高于材料抗压强度,再调整Ec和Ec使数值模型的割线模量与接触试验结果相近.接下来标定颗粒法向刚度与切向刚度的比值kn/ks,以及平行黏结法向刚度与切向刚度的比值kn/ks,标定目标值依据为接触试验割线模量(统计均值)对应的泊松比.最后标定平行黏结的法向和切向强度平均值(σc、τc),标定依据的目标值为试样抗压强度值.参数调试方法均参照PFC官方手册的建议进行.引入的强度折减参数则在实际模拟中根据破碎过程与形态调试得到.各向同性应力按岩石材料模拟经验取值.
通过数值模拟得到的大理石球-面接触模型主要参数如表 2所示.
| 表 2 球-面接触模型参数 Table 2 Modeling parameters of ball-surface contact simulation |
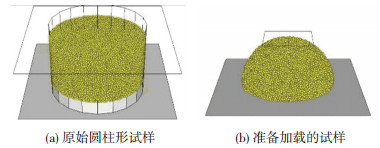
由于PFC3D程序中没有定义球形的墙单元,因此无法直接生成球形的数值模型.为解决此问题,本文采用的方法是先生成圆柱体数值模型,在颗粒之间充分接触后设置黏结,然后删除颗粒接触数小于3的颗粒,最后删除圆柱墙单元,并将圆柱体模型剪切成为半球模型,如图 9所示.
|
图 9 球-面接触数值模型示意 Figure 9 The diagram of ball-surface contact's model |
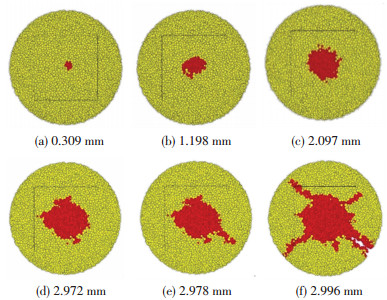
图 10所示为加载过程中半球模型球-面接触破碎形态变化俯视图.如前所述,试样中变为红色的部分表示该处的颗粒在加载过程中发生了黏结断裂,即该处发生了局部破碎.由图可知,开始加载后,半球模型的顶端由于应力集中发生局部破碎,随着加载的进行,破碎区域不断扩大.加载板向下位移2.978 mm时,在半球模型的右下方位置破碎区域连成一片,随后破碎面迅速发展,加载板向下位移2.996 mm时, 破碎面贯通,并形成次级裂缝,逐渐将试样分成4块,与室内大理岩球形颗粒球-面接触试验中颗粒整体破碎形态基本一致.
|
图 10 球-面接触破碎过程 Figure 10 The breaking process of ball-surface contact simulation |
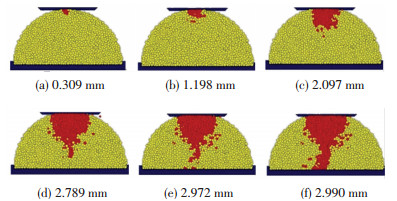
利用数值方法可以观察到半球形模型内部破碎区域的发展情况.在垂直于裂缝方向,通过接触面中心位置取剖面进行记录,即可观察到半球形模型内部破碎区域的发展情况,如图 11所示.可以观察到,破碎区域同时向水平方向和下部发展.破碎区域的剖面形状基本保持不变而范围不断扩大.破碎区域的发展速度在加载的前半段发展较慢,在加载板向下位移为2.789 mm时在局部破碎区域的前沿逐渐出现了破碎面,略早于俯视图中破碎面的出现.之后破碎面迅速发展到半球形模型底端并将半球形模型分成两半,试样整体破碎.
|
图 11 球-面接触破碎区域发展过程 Figure 11 The breaking area's development of ball-surface contact simulation |
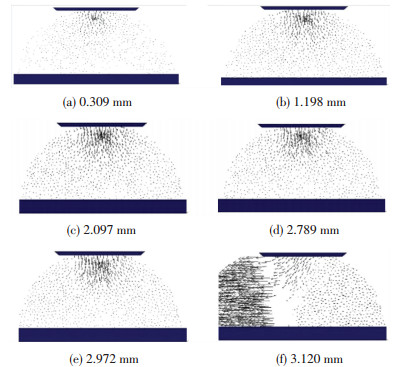
试样内部颗粒的位移可以反映试样中不同区域的局部破碎发展趋势,用以研究破碎规律.图 12为图 11剖面处一层颗粒的位移矢量图,箭头的方向代表颗粒位移的方向,箭头的长短代表位移的大小.通过观察位移矢量图,可以发现局部破碎区域的颗粒位移大于周围颗粒,局部破碎区域前端的颗粒向下运动,并使破碎区域不断向前发展.锥形的破碎区域发展到一定程度之后,逐渐挤压周围的颗粒向两侧运动,使试样发生整体破碎.
|
图 12 球-面接触颗粒位移 Figure 12 The diagram of particle displacement for ball-surface contact simulation |
图 13为数值模拟得到半球形模型的接触力-位移曲线.可以看出,在半球形模型整体破碎之前,接触力-位移曲线基本呈现线性变化,直线斜率为11.962(kN/mm).半球形模型在接触力33.78 kN时发生整体破碎.由于采用半球模型,底平面的数值基本颗粒无法与墙体生成黏结,与实际的对称模型边界条件存在差异,所以力-位移曲线与标定结果存在较大差异,但破碎形态和发展规律基本一致.

|
图 13 球-面接触数值模拟接触力-位移曲线 Figure 13 The force-displacement curve of ball-surface contact simulation |
数值模拟中采用两个直径为50 mm的半球形模型.考虑到颗粒总数的限制和计算效率问题,基本颗粒最小粒径取为3.0 mm.最大粒径与最小粒径的比值为1.8,颗粒总数约为30 000个.
在实际的计算中发现如果使用墙单元来进行加载,记录的位移为两个球变形的叠加,要远大于试验中的情况,会干扰数据分析.因此采用给其中一个半球固定的速度来进行加载.接触力通过另一个半球底部墙的反力来测量.
同样的,对于强度折减的影响范围在反复的计算中确定为发生黏结断裂的两个基本颗粒球半径之和的2.0倍.其余细观参数与球-面接触一致.
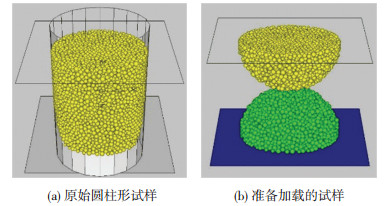
2.3.2 数值模型的生成使用和球-面接触模拟同样的圆柱体剪切法生成数值模型,高度为两个半球半径之和50 mm,见图 14.
|
图 14 球-球接触数值模型示意 Figure 14 The diagram of ball-ball contact's model |
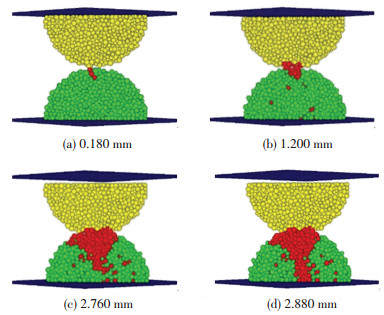
图 15为加载过程中半球形模型球-球接触破碎形态变化俯视图,图中去除了用于加载的半球.如前所述,试样中变为红色的部分,表示该处的颗粒在加载过程中发生了黏结断裂,即表示该处发生了局部破碎.加载位移为0.180 mm时,接触点处出现局部破碎,随后破碎区域不断发展扩大.加载位移为2.700 mm时在球的下部破碎区域连成一体形成了破裂面.加载位移为2.760 mm时破裂面逐渐贯通,直至2.880 mm破裂面完全贯通,试样整体破碎为两块.图 15(f)为从试样底部观察的图像,整体破碎裂缝通过底面圆心,将球分成大小基本相等的两块.从主要破碎面出现到试样整体破碎经过了0.180 mm的位移.

|
图 15 球-球接触破碎过程 Figure 15 The breaking process of ball-ball contact simulation |
利用数值方法可以观察试样内部破碎区域的发展规律.取垂直于裂缝方向且通过接触面中心位置的剖面观察,如图 16所示.与球-面接触情况相似,破碎区域同时向水平方向和下部发展.当加载位移为2.760 mm时,在破碎区域的前沿逐渐出现了破碎面,与通过俯视图判断的破碎面出现的阶段基本一致.之后破碎面迅速发展到试样底端,试样整体破碎为两半.与预期结果有所不同的是,不在接触点附近的区域也出现了局部破碎的情况.这可能是因为在试样生成过程中因局部没有完全密实而产生的小缺陷的影响,小缺陷类似于岩石材料中的天然节理.
|
图 16 球-球接触破碎区域发展过程 Figure 16 The breaking area's development of ball-ball contact simulation |
图 17为与图 16相同剖面处一层颗粒的位移矢量图,图中去除了未发生整体破碎的半球.通过观察位移矢量图,可以发现局部破碎区域呈锥形并逐渐发展,锥形区内部颗粒间位移矢量基本相同,推动前端的颗粒向下运动.锥形的破碎区域发展到一定程度之后,逐渐挤压周围的颗粒向两侧运动,使试样发生整体破碎.

|
图 17 球-球接触颗粒位移 Figure 17 The diagram of particle displacement for ball-ball contact simulation |
图 18为数值模拟得到的球-球接触模型的接触力-位移曲线,曲线在试样整体破碎前就出现了一个较大的波动.通过对数值模拟中加载过程的观察,发现曲线的波动是试样整体错动引起的.受限于建模方法,接触位置并不是规则的平滑表面,随着加载进行,球-球模型克服摩擦力发生了一定错动,这个过程被反映在了曲线的前半部分.与球-面接触试验的数值模拟相同,由于数值基本颗粒无法与墙体生成黏结,造成实际模拟中的边界条件与对称模型要求的边界条件不同,力-位移曲线与标定结果存在较大差异,但破碎形态和发展规律基本一致.

|
图 18 球-球接触数值模拟接触力-位移曲线 Figure 18 The force-displacement curve of ball-ball contact simulation |
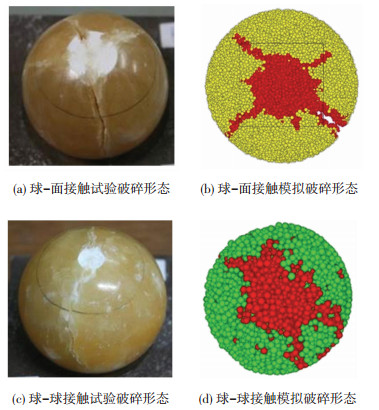
从破碎形态上来看,球-面接触与球-球接触的数值模拟结果均与室内试验相应的破碎形态基本一致,图 19为室内试验与数值模拟相对应的破碎形态对比图.球-面接触数值模拟的结果与球-面接触室内试验的结果比较接近.而球-球接触数值模拟的结果与球-球接触室内试验的差异相对较大.数值模拟中的锥形破碎区在外部轮廓与发展趋势上,与试验结果中的弹性核具有一定相似性.
|
图 19 试验与数值破碎形态对比 Figure 19 The comparison of shape between experiment and simulation after breakage |
而将图 13所示数值模拟结果与球-面接触模型试验得到的接触力-位移曲线对比,可以发现室内试验得到的曲线斜率约为数值模拟的两倍,颗粒整体破碎时对应的接触力与位移相差较大.同时由图 19可以发现,由于数值模拟总位移较大,发生整体破碎时的接触面积要比室内试验的结果大很多.原因除了边界条件与对称模型要求的不同之外,还因为PFC3D数值模型由小颗粒构成试样进行模拟,颗粒之间需要重叠才能进行力的传递,这使得模型具有一定散粒体的性质,而引入的强度折减参数又需要产生局部破碎才能发挥作用,因此才会导致整体破碎时的位移偏大.
通过对比室内试验与数值模拟的过程与结果,可以总结大理岩球形颗粒接触破碎的机理为:在球形试样顶部接触点处由于应力集中首先出现局部破碎并形成小平台.随着加载位移的增大,在平台之下形成了一个锥形体弹性核,其存在改变了力的传递路径.最后随着弹性核被压入,颗粒内某个薄弱截面由于达到抗拉强度而产生贯通裂缝,颗粒发生整体破碎.
尽管引入了强度折减参数的数值模拟结果不能用于定量分析力-位移关系,但模拟得到的颗粒破碎过程和颗粒整体破碎形态与室内试验比较接近,在用于结合室内试验分析破碎发展过程与机理时,这样的取舍是可以接受的.通过数值模拟,可以观察颗粒局部破碎和整体破碎的产生及发展过程并探究其机理.数值模拟结果是对室内试验一种较好的补充.
4 颗粒接触数值参数标定经验课题组通过不断的调试分析与总结,认为对于岩石等脆性材料,数值参数标定可以参考以下经验关系:
| $ {\bar E_{\rm{c}}} \approx 2{E_{\rm{c}}}, $ | (1) |
| $ \frac{{{k_{\rm{n}}}}}{{{k_{\rm{s}}}}} = \frac{{{{\bar k}_{\rm{n}}}}}{{{{\bar k}_{\rm{s}}}}} \approx 4.8, $ | (2) |
| $ {{\bar \sigma }_{\rm{c}}} = {{\bar \tau }_{\rm{c}}}. $ | (3) |
当岩石材料标准抗压强度在20~150 MPa时,Ec取值范围在1.0×108~1.0×1010 Pa或取单轴压缩试验标定值的约40%,σc取值范围在1.0×107~1.0×108 Pa或取单轴压缩试验标定值的约4倍.
对于本文使用强度折减参数,颗粒接触数值试验折减后的强度取值为原始强度的60%~80%,折减范围系数在两球半径和的1.2~2.5倍取值,具体参数根据颗粒破碎过程调整,并主要受数值基本颗粒的粒径分布影响,改变粒径分布后需要重新标定取值.
5 结论本文利用岩石双轴流变试验机进行了大理岩球形颗粒接触的球-面接触试验和球-球接触试验,并使用PFC3D模拟了大理岩球形颗粒接触加载和破碎过程,对室内试验结果进行了补充并进行对比,分析了颗粒破碎过程.主要结论如下:
1) 大理岩球形颗粒接触试验中,颗粒破碎为2~4块,在接触点处由于应力集中先发生局部破碎,逐渐形成锥形弹性核,其存在改变了法向接触力的传递路径,最终弹性核被压入导致颗粒发生整体破碎.
2) 本文的离散元数值模拟,在平行黏结模型中引入了强度折减参数,可以考虑应力集中对破碎区邻近区域强度的影响,能较好模拟室内试验中的颗粒整体破碎现象.
3) 数值模拟结果是对室内试验很好的补充,进一步明确了大理岩球形颗粒接触破碎过程的细观机理.本文总结了脆性材料颗粒接触数值参数标定经验,但仍需继续探索.
4) 本文只对粒径为5 cm的大理石球形颗粒接触破碎过程和机理进行研究,后续将进一步考虑粗粒土的颗粒大小、形状和岩性材料不同对颗粒接触破碎过程和机理的影响.
| [1] |
赵光思, 周国庆, 朱锋盼, 等. 颗粒破碎影响砂直剪强度的试验研究[J]. 中国矿业大学学报, 2008, 37(3): 291-294. ZHAO Guangsi, ZHOU Guoqing, ZHU Fengpan, et al. Experimental research on the influence of particle crushing on direct shear strength of sand[J]. Journal of China University of Mining & Technology, 2008, 37(3): 291-294. |
| [2] |
TERZAGHI K, PECK R B. Soil mechanics in engineering practice[M]. [S. l. ]: J. Wiley, 1948: 149-150.
|
| [3] |
LEE K L, FARHOOMAND I. Compressibility and crushing of granular soil in anisotropic triaxial[J]. Canadian Geotechnical Journal, 2011, 4(1): 68-86. |
| [4] |
MIURA N, YAMAMOTO T. Particle-crushing properties of sands under high stresses[J]. Technology Reports of the Yamaguchi University, 1976, 1: 439-447. |
| [5] |
HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177-1192. DOI:10.1061/(ASCE)0733-9410(1985)111:10(1177) |
| [6] |
POTAPOV A V, CAMPBELL C S. Parametric dependence of particle breakage mechanisms[J]. Powder Technology, 2001, 120(3): 164-174. DOI:10.1016/S0032-5910(01)00272-8 |
| [7] |
王强强. 粗粒土接触及破碎特性研究[D]. 上海: 同济大学, 2014. WANG Qiangqiang. A study on contact behaviors and particle breakage of coarse-grained soils[D]. Shanghai: Tongji University, 2014. |
| [8] |
杨光, 张丙印, 于玉贞, 等. 不同应力路径下粗粒料的颗粒破碎试验研究[J]. 水利学报, 2010, 43(3): 338-342. YANG Guang, ZHANG Bingyin, YU Yuzhen, et al. An experimental study on particle breakage of coarse-grained materials under various stress paths[J]. Journal of Hydraulic Engineering, 2010, 43(3): 338-342. |
| [9] |
王子寒. 粗粒土接触力学特性及细观本构关系研究[D]. 上海: 同济大学, 2013. WANG Zihan. A study on contact behaviors and microscopic constitutive relations of coarse-grained soils[D]. Shanghai: Tongji University, 2013. |
| [10] |
WANG W, COOP M R. An investigation of breakage behaviour of single sand particles using a high-speed microscope camera[J]. Géotechnique, 2016, 66(12): 1-15. |
| [11] |
TEJCHMAN J, GÓRSKI J, EINAV I. Effect of grain crushing on shear localization in granular bodies during plane strain compression[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2012, 36(18): 1909-1931. |
| [12] |
蒋明镜, 李秀梅. 双轴压缩试验中砂土剪切带形成的离散元模拟分析[J]. 山东大学学报(工学版), 2010, 40(2): 52-58. JIANG Mingjing, LI Xiumei. DEM simulation of the shear band of sands in biaxial test[J]. Journal of Shandong University(Engineering Science), 2010, 40(2): 52-58. |
| [13] |
COLE D M, PETERS J F. A physically based approach to granular media mechanics: grain-scale experiments, initial results and implications to numerical modeling[J]. Granular Matter, 2007, 9(5): 309-321. DOI:10.1007/s10035-007-0046-2 |
| [14] |
MANOUCHEHRIAN A, SHARIFZADEH M, MARJI M F, et al. A bonded particle model for analysis of the flaw orientation effect on crack propagation mechanism in brittle materials under compression[J]. Archives of Civil & Mechanical Engineering, 2014, 14(1): 40-52. |
| [15] |
尹小涛, 葛修润, 李春光, 等. 加载速率对岩石材料力学行为的影响[J]. 岩石力学与工程学报, 2010, 29(增刊1): 2610-2615. YIN Xiaotao, GE Xiurun, LI Chunguang, et al. Influences of loading rates on mechanical behaviors of rock materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(s1): 2610-2615. |
| [16] |
周韵鸿. 球形粗粒料法向接触及破碎特性研究[D]. 上海: 同济大学, 2017. ZHOU Yunhong. Fracture characteristics of coarse spherical particles under normal contact condition[D]. Shanghai: Tongji University, 2017. |
| [17] |
张津. 大理岩颗粒法向接触及破碎特性初步研究[D]. 上海: 同济大学, 2016. ZHANG Jin. A preliminary study on normal contact behaviors and particle breakage of marble samples[D]. Shanghai: Tongji University, 2016. |
 2018, Vol. 50
2018, Vol. 50


