2. 岩土及地下工程教育部重点实验室(同济大学),上海 200092;
3. 平顶山市公路管理局,河南 平顶山 467000
2. Key Laboratory of Geotechnical and Underground Engineering (Tongji University), Ministry of Education, Shanghai 200092, China;
3. Pingdiingshan Highway Administration, Pingdingshan 467000, He'nan, China
工程实践和研究已经表明岩体的应力和变形会在较长一段时期内不断发展和调整,甚至最后发生岩体破坏.流变特性是岩体的重要力学特性之一,研究岩体流变特性主要是研究岩体应力和变形随时间变化的规律,而蠕变和应力松弛则是岩体流变特性的两个重要方面.Griggs[1]很早就对灰岩、页岩和粉砂岩等软弱岩石进行了蠕变试验,指出只有当荷载达到一定值时,才会发生一定程度的蠕变,并研究了蠕变变形特征和本构关系.伊藤等[2]对花岗岩进行了30年的蠕变试验,结果表明,花岗岩同样呈现黏滞流动但未观测到屈服应力.20世纪五六十年代,陈宗基[3]率先将流变学应用于中国岩土工程领域,此后,中国许多学者对岩体的流变特性进行了研究[4-5].国内外学者对岩体蠕变特性的研究主要集中在完整岩石单轴和三轴蠕变试验方面,取得了较多研究成果[6-8].然而实际工程中由于结构面的存在,使得岩体与完整岩石的流变特性之间存在很大差异.不少学者对结构面的蠕变特性进行了研究.徐卫亚等[9]对无充填节理岩石进行了剪切流变试验,发现长期抗剪强度参数有所降低,且黏聚力对时间敏感性高于内摩擦角,并根据试验曲线建立了七元件非线性黏弹塑性剪切流变模型.沈明荣等[10]对锦屏Ⅱ级水电站引水隧洞中的绿片岩软弱结构面研究,得到了不同法向应力条件下岩体结构面的蠕变力学特性及其规律.张清照等[11]对规则齿形结构面进行蠕变试验,结果显示严格意义下的稳态蠕变是不存在的,常说的稳态蠕变实际上是蠕变速度随时间缓慢减小的近似稳态蠕变过程.虽然对结构面蠕变的研究取得了一定成果,但相对于岩石的蠕变研究来说还显得比较少.
对于岩体的流变特性而言,应力松弛现象在岩体工程中也是普遍存在的,例如巷道、地下工程及挡土墙等等,常常因围岩应力松弛而发生破坏[12].尽管人们认识到岩体松弛特性的重要性,但由于应力松弛试验采用变形恒定的试验控制方式,在早期的试验机中较难实现,因此应力松弛试验研究相对还比较少[13].随着岩体试验技术不断提高,有学者开始进行岩体应力松弛试验的研究.曹平等[14]采用分级增量加载方式对斜长角闪岩进行松弛试验,发现松弛曲线中存在连续型应力松弛和非连续阶梯型应力松弛.于怀昌等[15]对饱和粉砂质泥岩进行三轴压缩应力松弛试验,并用黏弹性模型来描述粉砂质泥岩的应力松弛特性.熊良宵等[16]对绿片岩进行单轴和双轴压缩应力松弛试验,并提出了经验拟合方程.田光辉等[17]通过规则齿型结构面在剪切应力条件下的应力松弛试验,研究结构面应力松弛规律.刘昂等[18]用岩石双轴流变试验机对水泥砂浆浇筑的Barton曲线结构面进行试验值大于剪切长期强度的循环加载剪切应力松弛试验,分析了结构面应力松弛特性,并提出通过应力松弛试验求解长期强度的方法.总体上看,虽然应力松弛的研究取得了一定成果,但与岩体蠕变特性的研究成果相比,应力松弛研究相对较少,而且现有松弛研究多集中在岩石单轴和三轴应力松弛特性研究方面,结构面松弛特性的研究成果则比较少.
刘雄[19]认为蠕变和松弛本质上是等价的,蠕变和松弛只是材料长期力学性质的两种理想化的力学概念,实质上它们为同一物理力学机制所控制.蠕变和松弛有着紧密的内在联系,而当前对岩体蠕变和松弛特性研究基本上是按各自特性分开进行的,十分有必要对岩体的蠕变特性和松弛特性进行综合对比分析,以便更好地了解长期荷载作用下岩体的力学特性,进而深入理解蠕变与松弛的区别和内在联系.
本研究为了减少试验结果的离散性和结构面复杂程度,采用规则齿形结构面试样,对结构面的蠕变特性和应力松弛特性进行试验研究.基于试验结果,分析不同爬坡角结构面蠕变特性和松弛特性的基本规律,及蠕变与松弛基本规律之间的异同;并对蠕变过程和松弛过程的剪应力-位移曲线进行比较分析;根据蠕变和松弛最终状态及速率变化特征,推导出基于蠕变速率,能够描述应力松弛特性的经验方程;分别根据蠕变试验和松弛试验确定结构面长期强度,并与蠕变过程和松弛过程中剪应力-位移曲线的屈服强度进对比.
1 试验材料与试验方法 1.1 试验设备本次试验所采用的仪器是长春试验机研究所生产的CSS-1950岩石双轴流变试验机(图 1).该试验机利用自带软件系统通过伺服电机控制试验过程,并自动采集试验数据,可以按试验要求设定采集精度.试验机可同时施加垂直轴向荷载和水平轴向荷载,也可分别施加.试验机垂直轴最大压力为500 kN,水平轴最大压力为300 kN.试样双轴双侧变形值可以同时测量,测量范围为±3 mm,测量精度0.001 mm.试验过程中,室内温度和湿度保持基本恒定.

|
图 1 试验装置 Figure 1 The test equipment |
为了减少因试样材料不同而造成试验结果的差异,所有试样采用相同的材料、配合比和养护时间.完整立方体试样和规则锯齿状结构面试样尺寸均为10 cm×10 cm×10 cm,其中锯齿状结构面单齿长度为10 mm,齿型个数为10,采用10°、30°和45°三种角度的爬坡角,10°爬坡角试样示意图及钢模,如图 2(a)~(c)所示.所有模型材料选用矿渣硅酸盐32.5R水泥、标准砂和水,配合比为水:水泥:砂=1:2:4.浇筑时,先把材料按配合比混合搅拌均匀,然后放入钢制模具中捣实,抹平表面,如图 2(d)所示.尽量减少试样制作过程中的不良影响.模型成型24 h后拆模,养护28 d.

|
图 2 结构面试样平面示意及制作过程 Figure 2 Ichnography of the dentate discontinuities and the process of making |
试验前期,先取3块完整立方体试样进行单轴抗压试验,得到其平均单轴抗压强度为19.62 MPa.为了便于试验结果比较分析,试验时法向应力选取完整立方体试样平均单轴抗压强度的10%,即1.962 MPa.
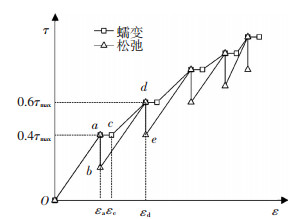
在蠕变和松弛试验前,取10°、30°和45°试样各3块进行直剪试验,取剪切应力与剪切位移曲线峰值作为抗剪强度.不同角度结构面试样的平均抗剪强度,如表 1所示.对试样进行不同应力水平的单级加载试验,需要试样较多,而且容易造成试验数据的离散性.因此,蠕变和松弛试验都采用分级加载的试验方法,施加的剪应力分别为各自爬坡角结构面平均抗剪强度τmax的40%、60%、80%、90%、95%.蠕变试验和松弛试验的应力路径,如图 3所示.
|
图 3 加载过程示意 Figure 3 The diagram of loading process |
| 表 1 不同角度结构面的平均抗剪强度 Table 1 Average shear strength of structural plane |
试验方法:1)蠕变试验,先施加法向应力至1.962 MPa,保持应力恒定,法向变形稳定后以0.2 kN/s速率施加剪应力至抗剪强度τmax的40%,即a点,然后保持剪应力恒定72 h,应变由a点增加到c点,之后以相同速率逐级施加设定好的剪应力级别,每级剪应力均保持72 h;2)松弛试验,先施加法向应力至1.962 MPa,保持应力恒定,法向变形稳定后以0.2 kN/s速率施加剪应力至抗剪强度τmax的40%,即a点,然后保持此时产生的应变εa恒定72 h,剪应力由a点松弛到b点,之后以相同速率逐级施加设定好的剪应力级别,保持每级剪应力下产生的应变恒定72 h.
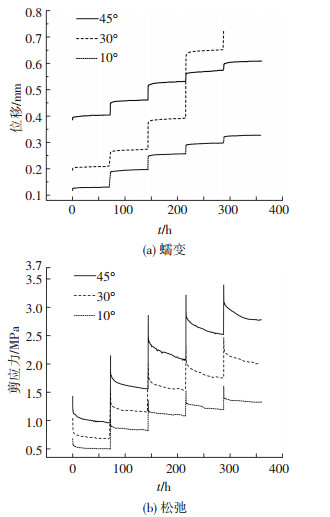
2 试验结果分析 2.1 蠕变与松弛基本规律试验按照上述方法进行,经过数据整理,得到如图 4所示的10°、30°和45°爬坡角结构面在相同法向应力和剪应力水平下的蠕变和应力松弛曲线.
|
图 4 结构面蠕变和松弛全过程曲线 Figure 4 The complete creep and relaxation curves |
从图 4不同爬坡角结构面的蠕变曲线和松弛曲线,可以看出:1)蠕变时应力恒定,变形随着时间的增长而增大,变形速率逐渐减小并趋近于零,曲线呈现上凸状.试验曲线整体为连续型蠕变曲线,随剪应力水平的增加,呈现明显的阶梯型;2)松弛时应变恒定,应力随着时间增长而减小,松弛速率逐渐减小并趋近于零,曲线呈下凹状.试验曲线也呈现出整体连续型应力松弛曲线,曲线表现出应力值阶梯型跌落,且为非完全应力衰减松弛曲线;3)不考虑试验加载段的瞬时变形时,蠕变曲线和松弛曲线形态相似,近乎于相互对称,但两者变化过程相反;4)图 4(a)所示30°爬坡角结构面的第4级蠕变变形异常增大,其原因可能是试样性质的差异造成30°结构面试样在第4级应力水平作用下发生屈服,产生的瞬时变形和蠕变变形都较大,而且与45°蠕变曲线发生交叉.试样在加载到第5级应力的过程中产生破坏,而松弛试验时试样没有破坏,其原因有一部分是试样差异性造成的,但主要原因是蠕变过程中试验机持续对试样做功,输入能量,当积累的能量大于试样破裂所需要的能量时就会产生破坏,而松弛过程是能量的释放,虽然试样差异性会造成破坏值的不同,但就一般而言,松弛一般不会产生破坏,而在应力加载过程中产生破坏.
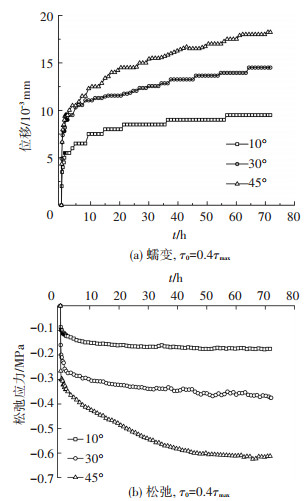
2.2 不同角度结构面的蠕变与松弛特征本次蠕变和松弛试验均采用分级加载的方法,采用第1级应力水平(即τ0=0.4τmax)下的蠕变和松弛数据进行分析.为了便于试验结果的对比分析,定义经历t小时松弛,剩余剪应力与初始剪应力的差值为松弛应力,τ0=0.4τmax应力水平下不同爬坡角结构面蠕变变形和松弛应力随时间变化的曲线,如图 5所示.
|
图 5 不同角度的蠕变和松弛曲线 Figure 5 Creep and relaxation curves of structure surface |
从图 5(a)蠕变变形与时间关系曲线可以看出,相同法向应力和剪应力水平下,爬坡角越大,剪切蠕变变形越大,衰减蠕变段也越明显,持续时间越长, 而且稳态蠕变段的速率越大,例如,蠕变时间在30~72 h范围内,10°、30°和45°爬坡角的稳态蠕变段曲线平均斜率分别为0.38×10-4、0.49×10-4和0.73×10-4 mm/h.爬坡角较小时,结构面主要为摩擦破坏,加载过程中积累的弹性变形能较少,爬坡角较大时,结构面主要表现为切齿破坏,加载过程中积累的弹性变形能较多,对试样造成的损伤也越大,因此产生的蠕变变形较大.本次试验得到的蠕变曲线变化规律与沈明荣等[20]的结论基本相同,即在相同的法向应力条件下,爬坡角越大,剪切蠕变变形越大.
由图 5(b)同一法向应力下不同爬坡角结构面松弛应力与时间的变化曲线可以看出:松弛曲线也可以分为衰减松弛和稳态松弛,松弛应力随着爬坡角的增大而增大,而且爬坡角越大,瞬时松弛量越大,过渡到稳态松弛持续时间也越长,稳态松弛段的平均速率越大.例如,松弛时间在30~72 h内,10°、30°和45°结构面的平均松弛速率分别为0.3×10-3、0.8×10-3和1.5×10-3 MPa/h.从能量的观点看,松弛是加载过程中积累的能量得到释放的过程,剪应力水平相同时,爬坡角越大,加载过程中积累的能量越多,在相同松弛时间内松弛应力和松弛速率都会越大,松弛到内外力平衡所需时间也越长.
从以上分析可以看出,同一剪应力水平点开始的蠕变试验和松弛试验,在应力加载过程中都会积累一定的弹性变形能,而且爬坡角越大,积累的能量越多,对试样造成的损伤也越大.当保持应力恒定进行蠕变时,损伤越大,产生的蠕变变形越多;当保持应变恒定进行松弛时,损伤越大,能量释放多,松弛应力和松弛速度也越大.因此,蠕变特性和松弛特性与加载过程中积聚在试样中的能量大小有关.
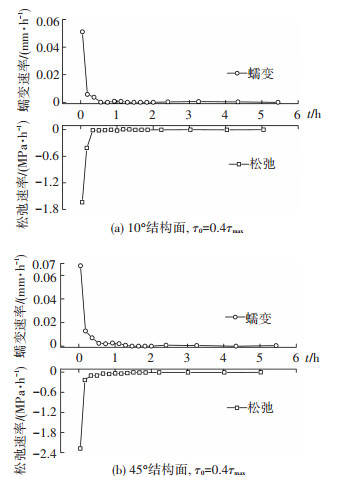
2.3 蠕变与松弛速率特性分析通过计算图 5结构面蠕变曲线和松弛曲线各个时刻的斜率,可以得到0.4τmax剪切应力水平下10°和45°结构面蠕变速率和松弛速率随时间的变化曲线,如图 6所示,横轴为时间,单位小时.试验结果显示蠕变曲线和松弛曲线一般在2 h以后基本趋于稳定,且速率很小接近于零,为清楚的显示和分析速率的变化过程,取前5 h的速率变化曲线描于图中.
|
图 6 不同角度蠕变速率和应力松弛速率曲线 Figure 6 Creep rate and relaxation rate curves of structure surface |
从图 6所示的蠕变速率和松弛速率曲线可以看出,蠕变过程中变形增加的速度逐渐减小,并趋于稳定,蠕变曲线的斜率为正值,松弛过程中应力减小的速度逐渐减小,并趋于稳定,松弛曲线的斜率为负值.因此图中蠕变速率从一个较大的正值减小到零,松弛速率从一个较大的负值减小到零,而且从图中可以清晰地看出:1)蠕变过程和松弛过程基本上都可以划分为衰减和稳态两个阶段;2)初始蠕变速率和初始松弛速率都随着结构面角度的增大而增大,如10°和45°爬坡角结构面的初始蠕变速率分别为0.051 1 mm/h和0.068 1 mm/h,初始松弛速率分别为1.638 6 MPa/h和2.278 3 MPa/h.两种速率曲线的变化特征与沈明荣等[20]、刘昂等[18]试验结果基本相同.
不考虑蠕变破坏的加速蠕变阶段,蠕变试验时,应力σ恒定(即应力速率
以45°爬坡结构面为例,蠕变试验过程中剪应力-位移曲线见图 7,松弛试验过程中的剪应力-位移曲线见图 8.

|
图 7 蠕变过程中剪应力与位移关系曲线 Figure 7 The shear stress-displacement curve during creep |

|
图 8 松弛过程中剪应力与位移关系曲线 Figure 8 The shear stress-displacement curve during relaxation |
1) 从图 7蠕变过程中剪应力和位移曲线可以看出:第1级应力加载过程中因试样两上下结构面接触不紧密及微裂隙张开,加载过程中试样先被压密,之后进入弹性段,曲线呈现下凹状,与一般直剪试验曲线相似;经第1级蠕变变形后,上下结构面接触紧密、微裂隙产生闭合以及胶结物发生压缩,试样产生一定的硬化现象.范秋雁等[21]也指出蠕变过程中微孔不断闭合及弱相不断被压缩,可变形结构强度不断提高,试样会产生硬化效应.因此第2、3级应力加载过程中,虽然会使试样微裂隙产生一定的扩展,但仍是硬化效应占主导地位,试样的剪应力-位移曲线近似呈线性变化.经过蠕变后,因岩石的变形记忆现象,变形曲线沿着原来单调加载曲线(如图中虚线)变化.第4、5级应力加载过程中,试样进入塑性屈服段(屈服点的应力约为2.8 MPa,与抗剪强度的比值为0.756),剪应力-位移曲线不再沿着原来单调加载曲线变化,开始向x轴发生偏移.
2) 松弛试验第1级应力加载过程的剪应力-位移曲线变化特征与蠕变试验相同.唐礼忠等[22]曾指出加载过程中岩石内部储存的弹性应变能,会使岩石产生新裂隙,破裂面滑动过程中弹性能会被释放.保持第1级应力产生的变形恒定开始松弛时,加载过程中积累的弹性变形能使试样内部强度不足的介质产生开裂或使微裂隙产生扩展,能量耗散大;当剩余的弹性变形能不足以再产生新的裂隙时,试样通过破裂面滑动等内部结构调整的方式消耗能量,直到内外力平衡.与蠕变硬化现象相似,松弛过程中的裂隙滑动挤压等内部结构调整,也会产生一定程度的硬化效应,如图 8各级应力水平加载段的剪应力-位移曲线明显为上凸状的孤线.刚开始时抵抗变形的能力较大,说明试样在再加载应力段产生硬化现象,当应力超出第1级初始松弛应力时,曲线回到原来的应力应变状态,此时硬化现象消失.之后,因岩石的变形记忆现象,曲线沿着原来单调加载曲线(如图中虚线)变化,这一特性与Haupt[23]得到的各松弛段典型应力-应变曲线相似.因试样的差异,松弛时,试样在第3级应力加载过程中产生屈服(屈服点的应力约为2.6 MPa,与抗剪强度的比值为0.724),与蠕变试验时的屈服点稍有差异.
蠕变试验和松弛试验中能量演化贯穿于始终.蠕变过程是外部不断给试样输入能量,而松弛过程是试样不断向外部释放能量.不考虑能量损失的条件下,能量可以用外力对岩石所做的功表示,即力-位移曲线围成的面积.由于功是不可逆的,图 7蠕变过程和图 8松弛过程的剪应力-位移曲线显示两类试验的应力-应变路径不同,可知蠕变过程和松弛过程中试样内的能量变化过程必定是不相同的,因此不能简单认为蠕变过程和松弛过程是等价的.
3 蠕变与松弛本构方程 3.1 蠕变本构方程从图 5、6可看出,蠕变时,既有瞬时变形,也有随时间增加的变形;松弛时,有瞬时应力降低,也有随时间增加而减小的应力.说明试样既有弹性又有黏性,幂律型的函数常被用来描述非线性黏弹性材料的应力、应变和时间的关系[24].因此,采用式(1)来描述蠕变过程:
| $ {\varepsilon _{\rm{c}}} = {\varepsilon _{\rm{i}}}{\rm{ + }}a{\sigma ^P}{t^b}. $ | (1) |
式中:εc是蠕变应变,εi是瞬时变形,σ是应力,a、p和b是材料常数.该式即反映加载过程中引起的瞬时变形,又考虑了蠕变过程中应力和时间的影响.采用最小二乖法对图 5中的蠕变曲线进行拟合,得到的相关系数都在0.95以上,与试验曲线吻合程度较高,对式(1)求导,可得蠕变变形速率方程为
| $ {{\dot \varepsilon }_{\rm{c}}} = ab{\sigma ^P}{t^{b-1}}, $ | (2) |
对式(2)进行整理,蠕变速率可写为
| $ {{\dot \varepsilon }_{\rm{c}}} = k{\sigma ^P}{t^n}. $ | (3) |
式(3)可反映应力与时间对蠕变速率的影响.
图 6显示的蠕变速率曲线和应力松弛速率曲线,形态相似,变化规律相同,而且试样是采用相同材料制成的,为对蠕变和松弛进行比较分析,采用同一函数形式描述松弛速率,应力松弛速率公式为
| $ \dot \sigma = k{\varepsilon ^P}{t^n}, $ | (4) |
式(4)同样可以反映应变水平与时间对应力松弛速率的影响.
用式(3)、(4)别对图 6蠕变速率曲线和松弛速率曲线拟合,吻合程度较高,相关系数都在0.95以上,可以较好地反映速率变化趋势.
3.2 松弛本构方程松弛试验时施加初始应变ε0 (ε0=σ0/E,σ0为初始应力,E为弹性模量),且ε0由弹性应变εe和非弹性应变εp组成,即式(5).松弛时,ε0恒定,应力σ随时间逐渐减小.
| $ {\varepsilon _0} = {\varepsilon _{\rm{e}}}{\rm{ + }}{\varepsilon _{\rm{p}}} = \frac{\sigma }{E} + {\varepsilon _{\rm{p}}}. $ | (5) |
松弛过程中ε0由于始终保持恒定,则在试验任意时刻dε0/dt=0,对式(5)求导,即可得到松弛过程中非弹性应变εp的速率方程:
| $ {{\dot \varepsilon }_0} = {{\dot \varepsilon }_{\rm{p}}} + {{\dot \varepsilon }_{\rm{e}}} = 0, $ | (6) |
| $ 即{{\dot \varepsilon }_{\rm{p}}} = - {{\dot \varepsilon }_{\rm{e}}} = \frac{{ - {\rm{d(}}\sigma /E{\rm{)}}}}{{{\rm{d}}t}}. $ | (7) |
松弛时,弹性模量E认为恒定,由式(5)可知,应力减小,则弹性应变εe减小,因初始应变ε0不变,非弹性应变εp增加.松弛过程可以看作是弹性应变εe逐渐转化为非弹性应变εp的过程[25-26].松弛过程中应力随时间增长而减小,非弹性应变随时间增长而增加,而蠕变也会引起非弹性应变随时间增加.因此松弛时,可以把非弹性应变εp看作是应力逐渐减小过程中,产生的一种蠕变变形.Siegel等[27]更是认为蠕变和松弛的本质是相同的,松弛的第一阶段对应过渡蠕变,松弛第二阶段对应稳态蠕变.松弛时,由于应力σ逐渐减小,由式(7)可知非弹性应变εp的速率也逐渐减小.根据上文分析,假定非弹性应变εp的速率变化规律附合蠕变应变εc的速率变化规律,即式(2),则分析非弹性应变εp速率时考虑了松弛应力和时间的影响,结合式(2)和式(7)得到:
| $ \frac{{-{\rm{d(}}\sigma /E{\rm{)}}}}{{{\rm{d}}t}} =-\frac{{{\rm{d}}\sigma }}{{{\rm{d}}t}}\frac{1}{E} =-ab{\sigma ^P}{t^{b - 1}}. $ | (8) |
根据应力松弛的初始条件,t=0时,σ=σ0,求解微分方程式(8),可得到松弛时应力与时间关系:
| $ \sigma {\rm{ = [}}\sigma _0^{1-p} + aE(p-1){t^b}{{\rm{]}}^{\frac{1}{{1 -p}}}}. $ | (9) |
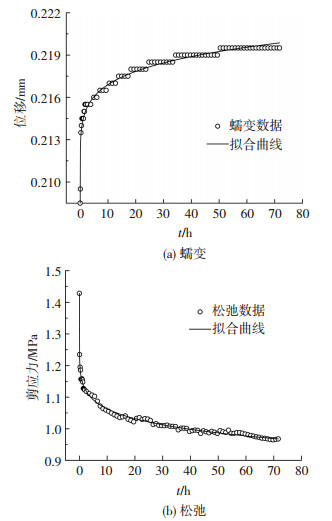
式中:σ0为初始应力,E为弹性模量,t为试验时间,a、p和b是材料常数.利用式(1)和式(9)分别对图 5中的10°和45°爬坡角结构面的蠕变曲线和松弛曲线进行拟合,拟合参数见表 2,拟合结果以45°爬坡角结构面为例,见图 9.
|
图 9 45°结构面模型拟合曲线 Figure 9 The fit curve of 45° discontinuities |
| 表 2 曲线拟合参数 Table 2 Parameter values of of curves |
从拟合结果可看出,蠕变方程和推导的松弛方程均能较好地反映结构面的蠕变和松弛过程,而且得到的相关系数较高,相关系数在95%以上.蠕变试验和松弛试验采用相同的试样、加载方法及应力水平,但表 2显示,拟合得到的材料常数a、p和n在蠕变试验和松弛试验中的值不同,相差较大,因此不能简单认为蠕变与应力松弛是等价的.于怀昌等[28]通过对粉砂质泥岩的蠕变以及应力松弛特性的对比研究,认为蠕变和松弛是不等同的.而张泷等[29]基于内变量热力学理论,认为蠕变和松弛是岩石材料在不同约束下的外在表现,但两者具有相同的非平衡演化规律,本质上具有一致性,且刘雄[19]、Siegel等[27]也认为蠕变和松弛的本质是相同的.因此,对蠕变和松弛的本质及相互关系需进一步研究分析.
4 长期强度 4.1 蠕变确定长期强度长期强度为岩石能保持长期稳定所能够承受的最大荷载,通常是根据蠕变试验采用间接方法确定岩石长期强度.过渡蠕变法是众多方法中比较常用、简单的一种.根据过渡蠕变法确定长期强度的机理可知,当施加的外部荷载小于或等于长期强度时,稳态蠕变速率应该为零;大于长期强度时,岩石存在某一稳定蠕变速率.张清照等[11]对规则齿形结构面剪切蠕变特性研究发现,无论低应力还是较高应力水平下,结构面稳态蠕变阶段的剪切蠕变速率均不是一个常数,而是随时间缓慢变化,只是在稳态蠕变阶段,变化幅度比较小,可以近似地认为是定常蠕变.换句话说就是,稳态蠕变阶段的蠕变并不是真正意义上的速率等于零,而是速率接近于零的常数.因此,可以根据稳态蠕变速率发生突然变化的拐点确定长期强度,而且文献[30-31]也将稳态蠕变速率拐点作为反映岩石长期强度的一个指标.
从图 4可看出,不同角度结构面试样在加载24 h后进入稳态蠕变阶段,取30~72 h之间的平均速率作为稳态蠕变速率.采用叠加原理可以得到分别加载时不同应力水平下的蠕变曲线,然后绘出10°和45°结构面稳态蠕变速率与应力水平的关系曲线,见图 10.因结构面的抗剪强度不同,施加的初始剪应力也不相同,为便于对比分析,图中横轴采用初始应力与抗剪强度的比值,即τ0/τmax.

|
图 10 稳态蠕变速率与应力水平关系曲线 Figure 10 Relationship between the steady-state creep rate and the stress level |
指数函数能较好地反映稳态蠕变速率与剪应力水平的关系[31].为精确确定稳态蠕变速率的拐点,本文先采用指数函数拟合稳态蠕变速率与剪应力水平的关系,如图 10所示,拟合得到的相关系数较高.指数函数没有明显的拐点,文中采用拟合曲线起点与终点切线的交点作为曲线的拐点,切线交点所对应的剪应力大小即为结构面的长期剪切流变强度,交点反映的是试样在剪切流变试验中由稳态蠕变进入加速蠕变的转折点.10°、30°和45°爬坡角结构面试样按此方法确定的两条切线交点对应的剪应力水平,即τ∞/τmax,分别为0.753、0.725和0.762,其平均值0.747,其中45°爬坡角结构面τ∞/τmax的比值与图 7所示45°结构面蠕变过程中力和位移曲线的屈服点强度与抗剪强度的比值0.756比较接近.取3个角度结构面τ∞/τmax的平均值0.747作为长期强度对应的应力水平,其结果与候宏江等[32]用相同的加载方式,对30°和45°爬坡角规则齿形结构面进行蠕变试验,采用等时曲线法确定长期强度为抗剪强度的0.8相差不大.
4.2 松弛确定长期强度松弛试验时,定义每级剪应力水平下初始应力τ0与经过时间t后的剩余应力τ(t)的差值为松弛应力Δτ,即Δτ=τ0-τ(t),式中,τ0为松弛试验刚开始时(即t=0时)的初始剪应力,τ(t)为经过时间t后的剩余应力,t为松弛时间.则每级剪应力水平下,经历72 h松弛后,松弛应力Δτ=τ0-τ(72).10°和45°结构面每级剪应力水平下松弛72 h产生的松弛应力Δτ与应力水平关系绘于图 11.为便于对比分析,横轴同样采用初始应力与抗剪强度的比值,即τ0/τmax.

|
图 11 松弛应力与剪应力水平曲线 Figure 11 Relationship between Δτ and shear stress level |
从图 11可看出,剪应力水平越大,松弛应力也越大,但松弛应力并不随着应力水平的增大一直增大,而是存在一个峰值.经研究发现,可以采用式(10)来描述松弛应力随应力平的变化规律.即
| $ y = {y_0} + \frac{1}{{2b}}{{\rm{e}}^{-\frac{{\left| {x-a} \right|}}{b}}}. $ | (10) |
式中:参数y0、a和b为常数,其中参数y0反映曲线的最小值,由公式可知其所描述曲线在x=a时,达到最大值y0+1/2b,即曲线峰值.采用式(10)对10°和45°结构面松弛应力Δτ随应力水平的关系曲线进行拟合,拟合结果见图 11,拟合参数见表 3.
| 表 3 松弛应力曲线拟合参数 Table 3 Parameter values of relaxation stress curve |
松弛应力峰值对应的应力为长期强度,其机理与过渡蠕变确定长期强度的机理相同[17].因此,可以根据式(10)拟合曲线峰值对应的x值,即参数a,作为长期强度τ∞与抗剪强度τmax的比值,其平均值为0.851,与根据蠕变试验确定的τ∞/τmax平均值0.747有所差别,但相差不大,相差约为9%.按此方法确定的45°爬坡角结构面τ∞/τmax的比值为0.784,与图 7所示45°结构面松弛过程中力和位移曲线的屈服点强度与抗剪强度的比值0.728比较接近.从能量的观点看,由于不可逆功的存在,蠕变过程输入的能量和松弛过程输入与释放的能量必定是不相等的,因此造成蠕变试验和松弛试验确定的长期强度略有差异,但相差不大.虽然蠕变试验和松弛试验确定的长期强度值相差不大,但从前文分析可知,蠕变和松弛过程中岩石内能量变化不同,不能简单的认为蠕变和松弛是等价的.
蠕变、应力松弛和长期强度是岩石流变的3个部分,岩石流变特性主要是将时间作为一个重要的因素,考虑岩石的力学特性受时间因素影响所做出的响应.从理论上看,岩石的蠕变、应力松弛和长期强度分别表示了变形、应力和强度与时间之间的关系.变形和应力可以认为是强度的两种外在表现形式,但殊途同归,蠕变试验和松弛试验都可以确定长期强度,而且两种方法确定的长期强度值相差不大,可以认为长期强度是岩石考虑时间因素后的最终状态.蠕变试验和松弛试验确定的长期强度值,分别与蠕变过程和松弛过程中剪应力-位移曲线的屈服强度比较接近,而且屈服强度值略小于两种试验确定的长期强度.关于屈服强度与长期强度的关系及屈服强度是否等于长期强度需要进一步地研究.
5 结论1) 不计瞬时变形时,蠕变曲线与松弛曲线形态相似,但过程相反.蠕变由于能量持续注入,位移增加,曲线呈上凸状;松弛因能量的耗散,应力减小,曲线呈下凹状.
2) 蠕变速率和松弛速率都随时间减小,而且速率变化曲线相似,可以采用同一函数形式描述.基于蠕变速率推导的松弛方程,能够较好地描述应力松弛过程,相关系数较高.
3) 典型蠕变方程和根据蠕变及松弛特性推导出的松弛方程均能较好地反映结构面的蠕变和松弛过程,曲线拟合相关系数也较高,但方程中材料常数的拟合值不等,公式只能反映曲线形态的变化,不能反映蠕变和松弛内在联系.而且蠕变和松弛应力-应变路径不同,由于不可逆功的存在,蠕变过程和松弛过程中的能量变化也不相同,因此不能简单认为蠕变和松弛是等价的.
4) 根据蠕变试验和松弛试验确定结构面的长期强度,其确定机理相同,但蠕变过程和松弛过程中的能量变化不同,使确定的长期强度值稍有差别.而且长期强度值与蠕变过程和松弛过程中剪应力-位移曲线的屈服强度比较接近.
| [1] |
GRIGGS D T. Creep of rocks[J]. Journal of Geology, 1939, 47: 225-251. DOI:10.1086/624775 |
| [2] |
ITO H, SASAJIMA S. A ten-year creep experiment on small rock specimens[J]. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr, 1987, 24(2): 113-121. |
| [3] |
陈宗基. 地下巷道长期稳定性的力学问题[J]. 岩石力学与工程学报, 1982, 1(1): 1-20. CHEN Zongji. The mechanical problems for the long-term stability of underground galleries[J]. Chinese Journal of Rock Mechanics and Engineering, 1982, 1(1): 1-20. |
| [4] |
钟时猷, 马明军. 软弱岩石蠕变破坏规律的探讨[J]. 中南矿冶学院学报, 1987, 18(5): 494-500, 590. ZHONG Shiyou, MA Mingjun. An approach to creep failure regularity of weak rock[J]. J Cent South Inst Min Metall, 1987, 18(5): 494-500, 590. |
| [5] |
孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999. SUN Jun. The rheology and engineering application of the geotechnical material[M]. Beijing: China Architecture and Building Press, 1999. |
| [6] |
TOMANOVIC Z. Rheological model of soft rock creep based on the tests on marl[J]. Mechanics of Time-Dependent Materials, 2006, 10(2): 135-154. DOI:10.1007/s11043-006-9005-2 |
| [7] |
赵旭峰, 孙钧. 海底隧道风化花岗岩流变试验研究[J]. 岩土力学, 2010, 31(2): 403-406. ZHAO Xufeng, SUN Jun. Testing study of rheological characteristics of weathered granite in undersea tunnel project[J]. Rock and Soil Mechanics, 2010, 31(2): 403-406. |
| [8] |
黄兴, 刘泉声, 康永水, 等. 砂质泥岩三轴卸荷蠕变试验研究[J]. 岩石力学与工程学报, 2016(增刊1): 2653-2662. HUANG Xing, LIU Quansheng, KANG Yongshui, et al. Triaxial unloading creep experimental study of sandy mudstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(s1): 2653-2662. |
| [9] |
徐卫亚, 杨圣奇, 褚卫江. 岩石非线性黏弹塑性流变模型(河海模型)及其应用[J]. 岩石力学与工程学报, 2006, 25(3): 433-447. XU Weiya, YANG Shengqi, CHU Weijiang. Nonlinear viscoelasto-plastic rheological model(Hohai model) of rock and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 433-447. |
| [10] |
沈明荣, 张清照. 绿片岩软弱结构面的剪切蠕变特性研究[J]. 岩石力学与工程学报, 2010, 29(6): 1149-1155. SHEN Mingrong, ZHANG Qingzhao. Study on the shear creep characteristic of greenschist discontinuity[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(6): 1149-1155. |
| [11] |
张清照, 沈明荣, 丁文其. 结构面的剪切蠕变特性及本构模型研究[J]. 土木工程学报, 2011, 44(7): 127-132. ZHANG Qingzhao, SHEN Mingrong, DING Wenqi. Study on the shear creep characteristics and constitutive model of rock mass discontinuity[J]. China Civil Engineering Journal, 2011, 44(7): 127-132. |
| [12] |
谢和平, 陈忠辉. 岩石力学[M]. 北京: 科学出版社, 2004. XIE Heping, CHEN Zhonghui. Rock mechanics[M]. Beijing: SciencePress, 2004. |
| [13] |
LADANYI B, JOHNSTON G H. Behavior of circular footings and plate anchors embedded in permafrost[J]. Canadian Geotechnical Journal, 1974, 11(4): 531-553. DOI:10.1139/t74-057 |
| [14] |
曹平, 郑欣平, 李娜, 等. 深部斜长角闪岩流变试验及模型研究[J]. 岩石力学与工程学报, 2012, 31(增刊1): 3015-3021. CAO Ping, ZHENG Xinping, LI Na, et al. Experiment and model study of rheological characteristics for deep amphibolite[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(s1): 3015-3021. |
| [15] |
于怀昌, 周敏, 刘汉东, 等. 粉砂质泥岩三轴压缩应力松弛特性试验研究[J]. 岩石力学与工程学报, 2011, 30(4): 803-811. YU Huaichang, ZHOU Min, LIU Handong, et al. Experimental investigation on stress relaxation properties of silty mudstone under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 803-811. |
| [16] |
熊良宵, 杨林德, 张尧. 绿片岩多轴受压应力松弛试验研究[J]. 岩土工程学报, 2010, 32(8): 1158-1165. XIONG Liangxiao, YANG Linde, ZHANG Yao. Stress relaxation tests on green schist specimens under multi-axial compression[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(8): 1158-1165. |
| [17] |
田光辉, 沈明荣, 周文锋, 等. 分级加载条件下的锯齿状结构面剪切松弛特性[J]. 哈尔滨工业大学学报, 2016(12): 108-113. TIAN Guanghui, SHEN Mingrong, Zhou Wenfeng, et al. Shear relaxation characteristic of serrate structure surface under stepwise loading[J]. Journal of Harbin Institute of Technology, 2016(12): 108-113. DOI:10.11918/j.issn.0367-6234.2016.12.015 |
| [18] |
刘昂, 沈明荣, 蒋景彩, 等. 基于应力松弛试验的结构面长期强度确定方法[J]. 岩石力学与工程学报, 2014(9): 1916-1924. LIU Ang, SHEN Mingrong, JIANG Jingcai, et al. Determining long-term strength of rock with discontinuity using shear stress relaxation test[J]. Chinese Journal of Rock Mechanicsand Engineering, 2014(9): 1916-1924. |
| [19] |
刘雄. 岩石流变学概论[M]. 北京: 地质出版社, 1994. LIU Xiong. Introduction to rock rheology[M]. Beijing: Geology Publishing House, 1994. |
| [20] |
沈明荣, 张清照. 规则岩体结构面的蠕变特性研究[J]. 岩石力学与工程学报, 2008, 27(增刊2): 3973-3979. SHEN Mingrong, ZHANG Qingzhao. Study on creep characteristics of regular rock mass discontinuity[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(s2): 3973-3979. |
| [21] |
范秋雁, 阳克青, 王渭明. 泥质软岩蠕变机制研究[J]. 岩石力学与工程学报, 2010, 29(8): 1555-1561. FAN Qiuyan, YANG Keqing, WANG Weiming. Study of creep mechanism of argillaceous soft rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1555-1561. |
| [22] |
唐礼忠, 潘长良, 谢学斌. 深埋硬岩矿床岩爆控制研究[J]. 岩石力学与工程学报, 2003, 22(7): 1067-1071. TANG Lizhong, PAN Changliang, XIE Xuebin. Study on rockburst control in deep-seated hard ore deposit[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(7): 1067-1071. |
| [23] |
HAUPT M. A constitutive law for rock salt based on creep and relaxation tests[J]. Rock Mechanics & Rock Engineering, 1991, 24(24): 179-206. |
| [24] |
FINDLEY W N, LAI J S, ONARAN K. Creep and relaxation of nonlinear viscoelastic materials: with an introduction to linear viscoelasticity[M]. Amsterdam: North-Holland, 1976.
|
| [25] |
YAHYA O M L, AUBERTIN M, JULIEN M R. A unified representation of plasticity, creep and relaxation behaviour of rock salt[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(5): 787-800. |
| [26] |
SINHA N K, SINHA S. Stress relaxation at high temperatures and the role of delayed elasticity[J]. Materials Science & Engineering A, 2005, 393(1/2): 179-190. |
| [27] |
SIEGEL M J, ATHANS D P. Relaxation of compression springs at high temperatures[J]. Journal of Fluids Engineering, 1970, 92(3): 627-632. |
| [28] |
于怀昌, 李亚丽, 刘汉东. 粉砂质泥岩常规力学、蠕变以及应力松弛特性的对比研究[J]. 岩石力学与工程学报, 2012, 31(1): 60-70. YU Huaichang, LI Yali, LIU Handong. Comparative study of conventional mechanical, creep and stress relaxation properties of silty mudstone under triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 60-70. |
| [29] |
张泷, 刘耀儒, 杨强. 基于内变量热力学的岩石蠕变与应力松弛研究[J]. 岩石力学与工程学报, 2015(4): 755-762. ZHANG Long, LIU Yaoru, YANG Qiang. Creep and relaxation of rock mass based on thermodynamics with internal state varibales[J]. Chinese Journal of Rock Mechanics and Engineering, 2015(4): 755-762. |
| [30] |
刘晶辉, 王山长, 杨洪海. 软弱夹层流变试验长期强度确定方法[J]. 勘察科学技术, 1996(5): 3-7. LIU Jinghui, WANG Shanchang, YANG Honghai. Method to determination the rheological test long-term strength for soft intercalations[J]. Site Investigation Science and Technology, 1996(5): 3-7. |
| [31] |
陈芳, 张强勇, 杨文东, 等. 坝区辉绿岩体的长期剪切流变强度分析研究[J]. 四川大学学报(工程科学版), 2011, 43(6): 91-97. CHEN Fang, ZHANG Qiangyong, YANG Wendong, et al. Analysis and research of long-term shear rheology strength of dam zone diabase[J]. Journal of Sichuan University(Engineering Science Edition), 2011, 43(6): 91-97. |
| [32] |
侯宏江, 沈明荣. 岩体结构面流变特性及长期强度的试验研究[J]. 岩土工程技术, 2003(6): 324-326, 353. HOU Hongjiang, SHEN Mingrong. Rheological properties of rock mass discontinuities and trial research of its long-term strength[J]. Geotechnical Engineering Technique, 2003(6): 324-326, 353. |
 2018, Vol. 50
2018, Vol. 50


