近年来,随着地下空间的开发利用,城市地下铁路建设和运营中的安全问题日益突出.一些潜在的威胁如地下水渗漏、突发洪水、有毒气体等一旦发生,将会造成巨大的危害,有效地阻止灾害蔓延成为降低损失的关键.1992年芝加哥突发洪水淹没了市中心隧道货运系统,由于未能及时阻隔洪水导致其蔓延范围迅速扩大[1],最终迫使25万人撤离,耗时一个多月才将水从隧道抽出,耗资4 000万美元[2-3].天津、上海等地区在修建地铁过程中,也出现了由地下水渗漏引起的安全问题[4-5],大量地下水涌入隧道,导致地表地下水位下降,进而对周围建筑物的沉降产生影响,致使其开裂甚至倾斜.因此,采用充灌气囊作为隧道抢险的临时性结构,具有质量轻、造价低、高效便捷的优点,其原理是增大气囊内压使之与隧道壁紧贴,利用与管壁之间的摩阻力将涌水、渗漏或有毒气体阻隔在气囊的一端[6].
国外学者曾提出气囊可作为安全装置应用于隧道的分区中,研究内容主要集中于气囊的安装、膨胀以及阻挡流体的效果,尚未涉及气囊受压后的具体变形以及失效模式的分析.Martinez等[7]针对隧道中突发的洪水或有毒气体,利用一个或数个气囊保护装置,安装固定在隧道顶部,险情一旦发生,便会触动开关机制,气囊可迅速膨胀,起到阻隔作用;Sosa等[8]进行了干、湿状态下气囊材料与混凝土面层的摩擦系数试验,并进行小比尺模型试验,气囊在摩阻力不足情况下会产生滑移;Sosa等[9]进行现场试验,将气囊安装在货运隧道中人行道的上方进行堵水试验,由于隧道形状存在较深的锐角,气囊与隧道壁不能完全贴紧,故在堵水过程中阴阳角处有漏水;Sosa等[10]用有限元模拟气囊的展开过程,包括气囊各边角的膨胀程度,研究不同模型模拟结果的差异,其中的模拟方法可用来预测工程中气囊的展开过程.目前,气囊在中国主要应用在小直径的输水、输气管道的堵漏中,且研究范围主要限于应用和操作方法.曾强[11]介绍了气囊式封堵的基本原理,设备构造特点和应用方法,并在实际工程管道中取得了良好的效果;王祖灿[12]分析计算了不同封堵形式、材料的管道堵漏效果,并采用气囊制作封堵装置,分析了气囊与管壁直径的匹配关系以及是否滑动与摩阻力的关系;蒋贤荣等[13]在宁波某给水主管道破裂事故中,采取旁通临时应急供水管道,破裂处两端设置气囊封堵的方法,完成了抢修任务,恢复供水;王天英等[14]研制了自粘式快速封堵气囊,并进行了模拟试验和海上现场试验;李明[15]提出大口径的气囊对材料的抗拉强度要求更高,通过试验说明在外压较小时堵水效果较好,外压增大至一定程度,气囊底部渗水使挡水将失效;张建等[16]提出球体薄壁压力容器的应力状态公式,对气枕式充气膜结构在不同外荷载作用下的受力状态进行分析.
以上国内外学者的研究均未涉及气囊在隧道中使用时的受力分析和变形特性以及气囊封堵失效的模式,而这正是气囊能否正常工作的关键问题.气囊是膜结构,四周受隧道壁的正向力约束,其能够抵挡的外压大小不仅由最大摩阻力决定,也取决于其形状变化的特点,因此研究气囊在外部气压或水压作用下的变形过程、滑移控制条件是十分必要的.在实际工程中设计气囊时,长度比较容易计算和控制,但直径在工艺上较难做到与隧道直径完全匹配,误差越小,气囊的匹配度越高,与隧道壁贴合的紧密性越好,对提高最大静摩阻力和封堵效果都有重要的意义.如何确定能使气囊正常工作的匹配度,即确定气囊直径的允许偏差范围是工程上亟待解决的问题,也是气囊设计的重点.
本文结合气囊在隧道中的边界条件,分别对气囊在均匀荷载和梯形荷载作用下进行受力分析,得出气囊形状的变化规律,确定气囊失效临界状态的形状和内外压关系以及失效模式.通过3种不同直径的气囊模型试验对理论结果进行验证,并分析不同匹配度的气囊变形和失效模式,得到气囊直径的允许偏差范围,为气囊在工程上的应用提供有效的理论依据.
1 理论分析 1.1 基本假定封堵气囊在隧道中用于堵气或堵水,气体为均布荷载,而水为梯形荷载,不同的荷载形式对气囊的变形和失效模式有一定的影响.为研究气囊在这两种荷载作用下的受力和形状变化,做出以下基本假定:
1) 隧道横截面为圆形.
2) 气囊为均质材料,刚度非常小,可以忽略不计,并忽略拉力作用下的延展性;与气囊内部压强相比,可忽略气囊自重.
3) 气囊一端受荷载后,内部气体满足气体状态方程:
| $ {p_0}{V_{\rm{a}}} = {p_1}{V_{\rm{b}}}. $ | (1) |
式中:p0为气囊未受荷时内部的压强,kPa;Va为气囊内部压强为p0时的体积,m3;p1为气囊受荷之后内部的压强,kPa;Vb为气囊内部压强为p1时的体积,m3.
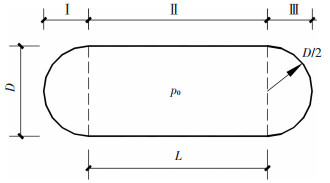
1.2 气囊的初始形状及受力分析气囊在内压作用下膨胀与隧道壁贴紧,左右两端(Ⅰ区、Ⅲ区)为半球体[17],中间部分(Ⅱ区)为圆柱体,沿中轴线的剖面图如图 1所示,设隧道直径为D,与隧道壁贴紧的圆柱体的长度为L,气囊上任意一点的张力为T0,计算式为
|
图 1 隧道中气囊的初始形状剖面图 Figure 1 The initial shape profile of the airbag in the tunnel |
| $ {T_0} = 0.25{p_0}D. $ | (2) |
当气囊左端受均布荷载时,首先确定气囊与隧道壁所产生的最大静摩阻力是否足够抵挡住外力,即气囊是否会被外力推动.在摩阻力满足条件的前提下,研究气囊在外力作用下的形状变化规律.
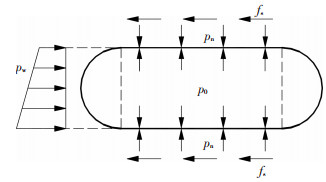
1.3.1 均布荷载作用下气囊受力分析在隧道中,当有均布荷载作用于气囊左端时,其受力分析的剖面图如图 2所示,气囊所受的力有:均布外荷载pw、内部气压力p0、隧道壁支撑力pn和摩阻力fs.

|
图 2 均布荷载下气囊受力分析 Figure 2 Force analysis of airbag under uniform load |
由受力分析图可知,在竖直方向上,外压作用在气囊Ⅰ区的合力Fwy为零(式3);在水平方向上,外力的合力Fwx,如式(4)所示.
| $ {F_{{\rm{w}}y}} = 0, $ | (3) |
| $ {F_{{\rm{w}}x}} = {p_{\rm{w}}}\frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}. $ | (4) |
气囊与隧道壁能够产生的最大静摩阻力如式(5)所示,其中μ是摩擦系数.由式(5)可知,最大静摩阻力与气囊直线段长度、摩擦系数、管壁对气囊的支持力呈正比.若气囊直径略大于或等于隧道内径,气囊内充满气即使内压为零,也可以完全与隧道壁接触.当给气囊内部充压时,隧道壁的支持力等于此时气囊内部压力,见式(5a);若气囊直径小于隧道内径,隧道壁的支持压力则等于气囊内部压力p0与pa的差值,见式(5b), 其中pa是指直径较小的气囊膨胀至与隧道壁贴合所需要的内压值.
| $ {F_{\rm{s}}} = \mu {p_{\rm{n}}}L{\rm{ \mathsf{ π} }}D, $ | (5) |
| $ {p_{\rm{n}}} = {p_{\rm{0}}}, $ | (5a) |
| $ {p_{\rm{n}}} = {p_{\rm{0}}} - {p_{\rm{a}}}. $ | (5b) |
由受力分析知,如果最大静摩阻力大于外力,气囊将不会产生整体滑移失效,在此基础上研究气囊受荷后的变形规律.
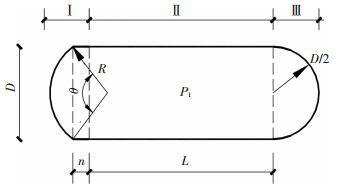
1.3.2 均布荷载作用下气囊变形分析气囊处于稳定工作状态下,其受力分析剖面图见图 3.当左端受到荷载pw时,气囊受荷端Ⅰ区的曲线段外部压力增大,内外压差减小,其上任一点形状r(x)由式(6)确定.内外压差在各点均相等,曲线段上各点拉力也相等,故曲线段为一段圆弧,半径为R,且大于D/2,圆心角为θ,弧长ly=R·θ.Ⅰ区的半圆形除形成此时的圆弧ly外,其余长度变形为贴壁的直线段,长度为n.变形后气囊形状参数n、θ随外压的增大而变化.
|
图 3 均布荷载下气囊形状剖面图 Figure 3 Profile of airbag under uniform load |
| $ r\left( x \right) = \frac{{{T_{1l}}}}{{{p_1} - {p_{\rm{w}}}}}. $ | (6) |
式中:pw为外部压强,kPa;p1为内部压强,kPa;r(x)为气囊Ⅰ区曲线上任一点的曲率半径;T1l为变形后气囊Ⅰ区圆弧的拉力,kN/m.
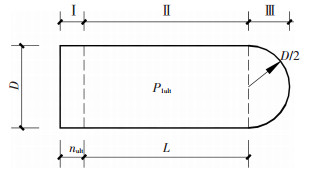
因为气囊是膜结构,只能承受拉力,T1l>0.由式(6)可知,当外力pw小于等于气囊内部压力p1时,圆弧的曲率半径为正,气囊能够保持其外凸的形状.反之,Ⅰ区圆弧段将内凹,此时没有外力可以平衡内凹曲线的张拉力,气囊形状不能保持,而且当外压大于内压时,外压能够抵抗气囊的内压力,气囊与隧道壁之间的支持力变为零,由式(5)可知,气囊摩阻力降低,气囊将会封堵失效.因此,在隧道中气囊能够正常工作的一个重要的控制条件是外部压力必须小于内部压力.当外压等于气囊内压时,气囊达到极限状态,左端形状接近于直线,如图 4所示.此时气囊Ⅲ区的张力最大,成为气囊材料拉力的控制条件.
|
图 4 均布荷载下极限状态时气囊形状剖面图 Figure 4 Limit profile of airbag under uniform load |
为确定外压作用下气囊的形状,即确定形状参数n、θ,利用3个方程:1)变形前后气囊总表面积相等;2)理想气体状态方程;3)功能原理.
1) 变形前后气囊表面积相等
气囊受外气压前表面积S为
| $ S = {\rm{ \mathsf{ π} }}{D^2} + {\rm{ \mathsf{ π} }}DL. $ |
变形后表面积S′为
| $ S' = \frac{{{\rm{ \mathsf{ π} }}D}}{{\sin \frac{\theta }{2}}}\left( {\frac{{0.5D}}{{\sin \frac{\theta }{2}}} - 0.5D\cot \frac{\theta }{2}} \right) + {\rm{ \mathsf{ π} }}Dn + \frac{1}{2}{\rm{ \mathsf{ π} }}{D^2} + {\rm{ \mathsf{ π} }}DL. $ |
令S =S′可得
| $ \frac{1}{2}{\rm{ \mathsf{ π} }}{D^2} = \frac{{{\rm{ \mathsf{ π} }}{D^2}}}{{2\sin \frac{\theta }{2}}}\left( {\frac{1}{{\sin \frac{\theta }{2}}} - \cot \frac{\theta }{2}} \right) + {\rm{ \mathsf{ π} }}Dn. $ | (7) |
2) 受荷前后囊内气体满足理想气体状态方程气囊受外气压前体积Va为
| $ {V_{\rm{a}}} = \frac{1}{6}{\rm{ \mathsf{ π} }}{D^3} + \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}L. $ |
气囊受外气压作用后体积Vb为
| $ \begin{array}{*{20}{c}} {{V_{\rm{b}}} = \frac{{\rm{ \mathsf{ π} }}}{6}\left( {\frac{{0.5D}}{{\sin \frac{\theta }{2}}} - \frac{{D\cot \frac{\theta }{2}}}{2}} \right)\left[ {\frac{3}{4}{D^2} + {{\left( {\frac{{0.5D}}{{\sin \frac{\theta }{2}}} - \frac{{D\cot \frac{\theta }{2}}}{2}} \right)}^2}} \right] + \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}n + \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}L + \frac{1}{{12}}{\rm{ \mathsf{ π} }}{D^3};}\\ {\frac{{{p_0}}}{{{p_1}}} = \frac{{{V_{\rm{b}}}}}{{{V_{\rm{a}}}}} = \frac{{D\left( {\frac{1}{{\sin \frac{\theta }{2}}} - \cot \frac{\theta }{2}} \right)\left[ {\frac{3}{4} + {{\left( {\frac{{0.5}}{{\sin \frac{\theta }{2}}} - 0.5\cot \frac{\theta }{2}} \right)}^2}} \right] + 3n + 3L + D}}{{2D + 3L}}.} \end{array} $ | (8) |
3) 功能方程
在外压作用下,气囊的变形满足功能方程,即气囊体积变化与内压p1的乘积等于外力做的功,δ为气囊的顶点的位移量.
| $ \begin{array}{*{20}{c}} {\delta = 0.5D - n - 0.5D/\sin \frac{\theta }{2} + 0.5D\cot \frac{\theta }{2},}\\ {\left( {{V_{\rm{a}}} - {V_{\rm{b}}}} \right){p_1} = \frac{1}{3}{p_{\rm{w}}} \times \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}\delta .} \end{array} $ | (9) |
联立式(7)~(9)可计算得到受荷后的气囊形状参数n、θ,即可得到气囊在任意外压pw下的形状以及变形后的内压p1.
1.3.3 均布荷载作用下气囊的失效模式对于受均布荷载的气囊有两种失效模式:第一种是尽管外压小于内压,气囊Ⅰ区的变形较小,只完成变形的一部分,未达到极限状态,但外力已经大于最大静摩阻力,从而导致气囊整体滑移;第二种是在施加外压的整个过程中,外力始终小于最大静摩阻力,但外压逐渐接近内压,气囊Ⅰ区的变形接近扁平的极限状态,当外压继续增大至足以平衡气囊内压,使隧道壁的支持力突变为零,外压将从接触面某薄弱处形成贯通气流,使气囊封堵失效,此时气囊的变形完全符合上文推导过程.
1.4 梯形荷载作用下气囊受力变形及失效模式分析当梯形荷载作用在气囊上,首先分析在外力作用下气囊的摩阻力是否足够,即气囊会否发生整体滑移失效,在摩阻力足够的前提下,分析气囊在外力增长过程中的变形特点.
1.4.1 梯形荷载作用下气囊受力分析在隧道中,当有梯形荷载作用于气囊左端时,气囊受力剖面图如图 5所示,假设水压水头为H,气囊所受的力有:梯形外荷载pw、内部气压力p0、隧道壁支撑力pn和摩阻力fs.
|
图 5 梯形荷载下气囊受力分析 Figure 5 Force analysis of airbag under trapezoidal load |
由受力分析图可知,在竖直方向上,外力合力为Fwy;在水平方向上,气囊所受水平外力Fwx如式(11)所示.
| $ {F_{{\rm{w}}y}} = \frac{1}{{12}}\gamma \cdot {\rm{ \mathsf{ π} }} \cdot {D^3}, $ | (10) |
| $ {F_{{\rm{w}}x}} = \frac{1}{4}{\rm{ \mathsf{ π} }}{D^2}\gamma \left( {H - \frac{D}{2}} \right). $ | (11) |
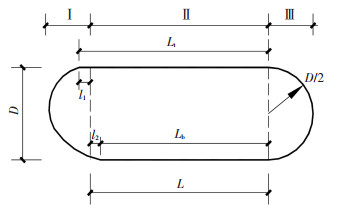
由上述受力分析可知,在竖直方向上外力合力向上,在外力作用下气囊有向上变形的趋势,而向上的外力需要隧道壁的支持力来平衡,因此气囊顶部的直线贴壁段将会变长而底部变短,当外压等于内压时,变形达到极限状态,此时顶部直线段长为Lt,底部直线段长为Lb,曲线段在最底部与直线段相切,见图 6.
|
图 6 梯形荷载下极限状态时气囊形状剖面图 Figure 6 Limit profile of airbag under trapezoidal load |
| $ {L_{\rm{t}}} = L + {l_1},{L_{\rm{b}}} = L - {l_2}. $ |
式中l1、l2分别为气囊变形后顶部增加、底部减少的直线段长度.
1.4.3 梯形荷载作用下气囊的失效模式对于受梯形荷载的气囊同样有两种失效模式:第一种失效模式与均布荷载相似,仅在外力的算法上有所不同;第二种在满足外力小于最大静摩阻力这个条件下,由于梯形荷载的底部外压最大,故气囊底部是最薄弱的地方.当底部外压等于内压时,气囊底部变形至极限状态后,水压将顶开底部气囊,形成贯通水流向外喷出,此时气囊虽未整体滑动,但封堵已经失效.
2 模型试验为研究不同直径匹配度的气囊在气压和水压作用下各自的变形特性和滑移失效机制,验证上文理论假设和分析的正确性,进行缩比尺模型试验.选用气囊材料为聚氯乙烯,与其承受的内压相比可忽略其自重,材料薄而柔软,不具有抗弯刚度,与实际工程中的气囊具有相同的变形特性,缩尺试验可以较好地反映现场试验中的规律性.
2.1 试验装置1) 模型隧道.为更加直观地观察气囊受荷端的变形,采用透明有机玻璃材料制作模型隧道,隧道长2 m,内径0.4 m,内环周长为125.66 cm.左端封闭并设置注气孔、注水孔、排水孔以及测压孔.在左侧施加侧压力,右端敞口,如图 7中①所示.经试验测定,有机玻璃与气囊材料的摩擦系数μ=0.31.

|
图 7 气囊挡气、挡水试验装置 Figure 7 Test device of airbag for blocking air and water |
2) 气囊.根据隧道直径来确定不同匹配度的气囊直径,直径适中的气囊是指在零内压下气囊可以贴紧隧道壁且没有初始褶皱的气囊;本试验选用直径偏大的气囊,周长误差在+5%以内,存在初始不贯通的褶皱;选用直径偏小的气囊,在一定内压下才能贴壁.不同直径误差的3个气囊,尺寸如表 1所示.其中直径偏大和适中的气囊在内压为零时便可与隧道壁贴合,直径偏小的气囊需使内压达一定值后才能贴合,气囊如图 7中②所示.
| 表 1 3个气囊的尺寸 Table 1 The sizes of three airbags |
3) 压力泵和水压供给装置.试验采用气压来模拟外部的均布荷载,用水压来模拟梯形荷载,压力泵用来提供气囊内部压力以及外部气压,水压供给装置用以提供外部水压力,分别如图 7③、④所示.
4) 测压表和采集仪.测压表用来测量气囊实时内压和外部水压、气压,连接至采集仪,记录压力变化,如图 7⑤所示.
2.2 试验过程对直径适中、偏大、偏小的3种气囊进行气压、水压作用下的模型试验,不断增大外压直至气囊封堵失效.记录在外压增长过程中气囊形状和内压的变化,以及气囊即将失效极限状态时的内外压关系.改变气囊的初始内压,得到不同内压下气囊形状的变化规律和失效的临界状态.
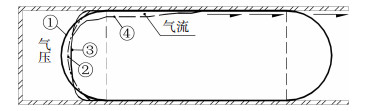
3 直径适中气囊的试验结果及分析 3.1 均布荷载作用下试验结果分析 3.1.1 试验现象及气囊形状变化直径适中的气囊与隧道匹配性较好,在内压9.8 kPa作用下与管壁贴合非常紧密,没有轴向褶皱,初始形状符合理论假设,见图 8的状态①.在外部气压作用下,气囊左端逐渐扁平,右端以及与管壁接触的直线段形状没有变化,见图 8的状态②.当外压增大至接近内压时,气囊左端呈扁平态(状态③为临界状态),一旦超过此临界状态,气压足以平衡气囊内压,使得隧道壁的支持力突变为零,接触面薄弱处(上端)会迅速被外压撑顶开,气囊凹陷,气流在此处沿轴向蔓延,很快便贯通整个气囊,带动气囊发生错动,挡气失效,如状态④所示.改变气囊初始内压进行多次试验,得到的试验现象比较一致.
|
图 8 直径适中的气囊在外气压下的变形过程 Figure 8 Deformation process of airbag with moderate diameter under external air pressure |
因为直径适中的气囊内压增长和形状变化最接近理论值,故将上述试验过程中气囊的形状参数(n、θ)和内压p1变化的试验值和理论值对比于表 2.
| 表 2 气压下直径适中的气囊形状及内压随外压变化 Table 2 Change of shape and internal pressure of the airbag under air pressure |
由表 2可以看出,试验中初始状态时气囊Ⅰ区不是标准的半圆,即n′值不为零,且θ′值不是π.在外压增长的过程中,试验得到的气囊内压p1逐渐增大,气囊Ⅰ区的形状参数n′逐渐增大,而圆心角θ′逐渐减小,与理论计算得到内压值和形状参数较为吻合,证明了理论推导的适用性.
3.1.2 气囊失效模式分析将多次试验中气囊临界状态时的外压、内压以及计算得到的外力和最大静摩阻力汇总于表 3.根据上述理论分析得知,气囊失效分为两种模式,由表 3可知,在失效的临界状态时,此时的外力远远小于气囊与管壁间的最大静摩阻力,说明此时气囊失效并不是摩阻力不足引起的.此时外压等于气囊内压,Ⅰ区的变形也接近扁平的极限状态,可以看出这属于第二种失效模式.
| 表 3 气压下直径适中的气囊极限状态时的内外压 Table 3 Internal and external pressure of the airbag with moderate diameter at limit state under air pressure |
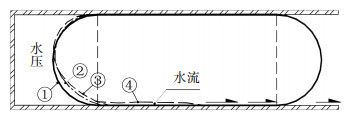
当气囊初始内压为10 kPa,形状如图 9的状态①所示.从左侧向管内注水,在水压作用下气囊左端下部有向上移的趋势,当外压在3 kPa左右时,水开始从气囊底部缓缓浸入,而后自管道右端呈滴水状态流出,此时没有形成贯通的流淌,气囊与管壁依然贴紧,浸水不影响气囊对水的阻漏.随着外压的增大,气囊变形明显,由于气囊最底处所受外压最大,左端下部气囊上移显著,如图 9状态②所示.水压继续增大,当底部外压等于内压时,气囊变形达到极限状态,左端曲线底部与直线段相切,如图 9状态③所示,此为气囊挡水的临界状态,外压继续增大,将会形成贯通的水流,从气囊底部右侧淌出,气囊挡水失效,如图 9状态④所示.
|
图 9 直径适中的气囊在外水压下的变形过程 Figure 9 Deformation process of airbag with moderate diameter under external water pressure |
将试验结果汇总于表 4,表 4中外压指的是气囊底部的水压,由表 4可以看出,此气囊阻水失效是因为外压等于内压的缘故.
| 表 4 水压下直径适中的气囊极限状态时的内外压 Table 4 Internal and external pressure of the airbag with moderate diameter at limit state under water pressure |
将气囊充气使其内压为18 kPa,由于气囊周长偏大,放入管道后不可避免的出现褶皱,褶皱不贯通,分为左右两小段,如图 10状态①所示.当外压较小时,气密性较好,左端产生变形,如状态②所示.在外压等于内压时,左端变形至极限状态,如状态③所示.当外压继续增长时,气囊左端会瞬时产生较大的扭转和错动,错动后气囊上两段褶皱迅速连续而贯通,变成一条贯通的褶皱,如状态④所示,气流顺着贯通的褶皱流走,气囊封堵失效.

|
图 10 直径偏大的气囊在外气压下的变形过程 Figure 10 Deformation process of airbag with larger diameter under external air pressure |
由表 5可知,直径偏大的气囊在外气压作用下,失效模式同样是外压大于内压,即说明直径偏大气囊虽然失效的过程与直径适中的气囊略有差异,但阻气的效果基本一致.因此,直径较大的气囊只要在允许偏差范围内,可以满足其堵漏的要求.
| 表 5 气压下直径偏大的气囊极限状态时的内外压 Table 5 Internal and external pressure of the airbag with larger diameter at limit state under air pressure |
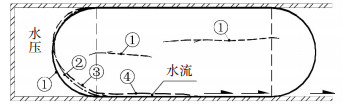
气囊初始内压为15 kPa,初始有不贯通的皱褶,形状如图 11的状态①所示.在外部水压增大过程中,其试验现象与直径适中的气囊在水压作用下的表现相似,不再赘述.
|
图 11 直径偏大的气囊在外水压下的变形过程 Figure 11 Deformation process of airbag with larger diameter under external water pressure |
将试验结果汇总于表 6,可以看出,气囊阻水失效是因为底部外压等于内压的缘故.虽然气囊存在初始的褶皱,但其最薄弱的地方也同样是气囊底部,此失效模式与直径适中气囊非常相似.
| 表 6 水压下直径偏大的气囊极限状态时的内外压 Table 6 Internal and external pressure of the airbag with larger diameter at limit state under water pressure |
试验中直径偏小的气囊左端0.8 m范围内截面周长为119.2 cm,当内压小于35 kPa时,都无法与管壁接触;右端0.3 m范围内截面周长为124.3 cm,当内压等于4.8 kPa时,刚好与管壁接触.
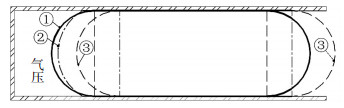
将气囊内压充至10 kPa,此时只有右端0.3 m范围内气囊贴到管壁,整体上无任何褶皱,如图 12的状态①所示.随着外压增大,气囊左端产生微小的变形,如状态②所示.在外压达到一定值时,气囊整体发生滑动,相对于隧道产生较大的位移,如状态③所示.直径偏小的气囊在挡气失效的过程中没有出现左端形状十分扁平的极限状态,这是由于其外压远远小于内压时便发生了滑动.
|
图 12 直径偏小的气囊在外气压下的变形过程 Figure 12 Deformation process of airbag with smaller diameter under external air pressure |
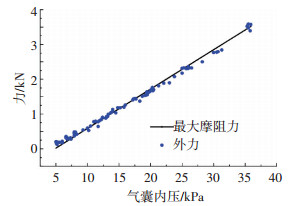
由试验统计结果得,在气囊滑动失效时,气囊外压与内压之比为0.5~0.75,将外压和内压带入式(4)、(5)计算此时的外力和摩阻力,因为左端0.8 m没有贴合上,右端0.3 m在内压4.8 kPa时才贴上,故式(5)中贴壁段长度L取值为0.3 m,pa取值为4.8 kPa,将滑动极限状态的外力和最大静摩阻力绘于图 13.气囊所受外力等于最大静摩阻力,可判断该气囊是由于摩阻力不足而引起的滑移失效.
|
图 13 气压下气囊滑动临界状态时的最大摩阻力和外力 Figure 13 The maximum friction and external force of the airbag in the sliding critical state under air pressure |
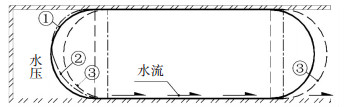
随着水压增大,气囊左端产生一定微量的变形,而且出现浸湿现象,逐渐向右蔓延,管道右端有水滴落,见图 14.当水压继续增大至一定程度时,气囊在水压的推动下产生滑移.
|
图 14 直径偏小的气囊在外水压下的变形过程 Figure 14 Deformation process of airbag with smaller diameter under external water pressure |
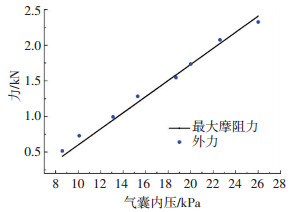
由试验统计结果得,气囊外压与内压之比为0.75~0.8,将外压和内压带入式(11)、(5)计算得到此时的外力和摩阻力,将滑动极限状态的外力和摩阻力绘于图 15.同样,此时气囊外力等于其最大静摩阻力,可判断该气囊在水压作用下也是由于摩阻力不足而引起的滑移失效.
|
图 15 水压下气囊滑动临界状态时的最大摩阻力和外力 Figure 15 The maximum friction and external force of the airbag in the sliding critical state under water pressure |
根据上文模型试验可知,气囊直径略微偏大时,不影响其堵水、堵气的效果,但直径的上限以充灌后不出现贯通的缝隙为准;气囊直径偏小时,需先充灌一定内压才能使其紧贴于隧道壁,此部分内压不能使气囊受到隧道有效的支持力以增加摩阻力,尤其对于延展性较差的材料是非常不利的.设计气囊直径的下限为充灌后隧道壁对气囊的支持力形成的最大摩阻力满足整体受力平衡的条件.
已知需要封堵的外力值,需使气囊的内压大于外压,以保持气囊形状的稳定,避免发生第二种失效破坏;在确定了气囊内压和截面周长后,通过式(5)计算得到气囊满足使用要求的直线段长度L,以保证最大静摩阻力大于外力,避免发生第一种失效破坏.通过式(2)可选择合适强度的气囊材料,以保证其抗拉强度大于气囊的拉力.通过以上步骤确定了所需气囊的内压、直径、长度和材料类型,从而实现封堵效果.
6 结论1) 通过对气囊在均匀荷载和梯形荷载作用下进行受力分析,结合状态方程,得到了气囊在两种不同荷载作用下形状的变化规律以及其变形的极限状态.梯形荷载作用时,气囊底部是最薄弱的环节.
2) 无论是均布荷载还是梯形荷载作用时,气囊都具有两种失效模式,一种是外力大于摩阻力的整体滑移失效,另一种是外压大于内压引起的气囊形状失稳变形而失效.
3) 通过模型试验可得直径适中的气囊密封性很好,气囊内压增长、变形特性和失效模式完全符合理论公式;直径偏大的气囊有初始褶皱,密封性较好,变形和失效类似直径适中的气囊;直径偏小的气囊,容易造成摩阻力的不足而造成封堵失效.
4) 已知气囊需封堵的外压时,可先确定气囊的内压,确定气囊直径原则是:直径上限以充灌后不出现贯通的缝隙为准,直径的下限为充灌后隧道壁对气囊的支持力形成的最大摩阻力满足整体受力平衡的条件.进而计算气囊应有的长度以及材料强度.
| [1] |
MENKUS B. The lessons of the great Chicago flood of 1992[J]. Computers & Security, 1992, 11: 417-420. |
| [2] |
INOUYE R R, JACOBAZZI J D. Great Chicago flood of 1992[J]. Civil Engineering-asce, 1992, 62(11): 52-55. |
| [3] |
郑永来, 李美利, 王明洋, 等. 软土隧道渗漏对隧道及地面沉降影响研究[J]. 岩土工程学报, 2005, 27(2): 243-247. ZHENG Yonglai, LI Meili, WANG Mingyang, et al. Study on influence of seepage of metro tunnels in soft soil on the settlements of tunnels and ground[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(2): 243-247. |
| [4] |
刘凯利, 闻宝联, 刘春波, 等. 天津地铁既有线渗漏水综合治理[C]//中国防水堵漏保温技术高峰论坛论文集. 天津: 中国硅酸盐学会房建材料分会防水材料专业委员会, 2006: 187-191. LIUKaili, WEN Baolian, LIU Chunbo, et al. Integrated leak treatment for tunnel of Tianjin subway existing line[C]//Collection of China waterproof and plugging Insulation Technology Summit Forum. Tianjin: Waterproofing materials Specialized Committee of Housing construction materials branch of The Chinese Ceramic Society, 2006: 187-191. |
| [5] |
吴怀娜, 胡蒙达, 许烨霜, 等. 管片局部渗漏对地铁隧道长期沉降的影响规律[J]. 地下空间与工程学报, 2009, 5(增刊2): 1608-1611. WU Huaina, HU Mengda, XU Yeshuang, et al. Law of influence of segment leakage on long-term tunnel settlement[J]. Chinese Journal of Underground Space and Engineering, 2009, 5(s2): 1608-1611. |
| [6] |
江庆海. 地下管道施工及疏通维修工程气囊封堵施工技术[J]. 黑龙江科技信息, 2013, 22: 258-258. JIANG Qinghai. Construction technology of airbag blocking for underground pipeline construction and dredging maintenance[J]. Heilongjiang Science and Technology Information, 2013, 22: 258-258. |
| [7] |
MARTINEZ X, DAVALOS J, BARBERO E, et al. Inflatable plug for threat mitigation in transportation tunnels[C]//In Proceedings of the Society for the Advancement of Material and Process Engineering (SAMPE) 2012 Conference. Baltimore, Maryland: [s. n. ], 2012.
|
| [8] |
SOSA E M, THOMPSON G J, BARBERO E J, et al. Friction characteristics of confined inflatable structures[J]. Friction, 2014, 2(4): 365-390. DOI:10.1007/s40544-014-0069-8 |
| [9] |
SOSA E M, THOMPSON G J, BARBERO E J. Testing of full-scale inflatable plug for flood mitigation in tunnels[J]. Transportation Research Record Journal of the Transportation Research Board, 2014, 2407: 59-67. DOI:10.3141/2407-06 |
| [10] |
SOSA E M, WONG C S, ADUMITROAIE A, et al. Finite element simulation of deployment of large-scale confined[J]. Thin-Walled Structures, 2016, 104: 152-167. DOI:10.1016/j.tws.2016.02.019 |
| [11] |
曾强. 管道封堵气囊在管道检修中的应用[J]. 水利建设与管理, 2015, 35(9): 76-77. ZENG Qiang. Application of pipeline plugging airbag in pipeline maintenance[J]. Water Conservancy Construction and Management, 2015, 35(9): 76-77. |
| [12] |
王祖灿. 用于钢管、PE管的吹扫、试压、临时封堵装置的研发[D]. 广州: 华南理工大学, 2013. WANG Zucan. A device used for temporary plugging of steel or PE pipes during pressure test and pipe cleaning[D]. Guangzhou: South China University of Technology, 2013. |
| [13] |
蒋贤荣, 谢遵哲, 王鹏. 大口径给水主管破裂的应急抢修技术措施[J]. 中国给水排水, 2010, 26(8): 101-103. JIANG Xianrong, XIE Zunzhe, WANG Peng. Technical measures for urgent repairing of large diameter water supply main pipeline break[J]. China Water Supply and Drainage, 2010, 26(8): 101-103. |
| [14] |
王天英, 刘娜, 李超芹, 等. 海底管道泄漏快速封堵试验[J]. 油气储运, 2015, 34(6): 657-661. WANG Tianying, LIU Na, LI Chaoqin, et al. Rapid plugging test of submarine pipeline leakage[J]. Oil & Gas Storage and Transportation, 2015, 34(6): 657-661. |
| [15] |
李明. 关于气囊堵水技术在超大口径给排水管中的应用探讨[J]. 广东科技, 2012(3): 108-109. LI Ming. Application of plugging gasbag in large diameter pipeline[J]. GD Science & Technology, 2012(3): 108-109. |
| [16] |
张建, 杨庆山, 李波. 气枕式充气膜结构形态与受力分析[J]. 哈尔滨工业大学学报, 2008, 40(12): 2020-2023. ZHANG Jian, YANG Qingshan, LI Bo. Form-state and loading analysis of air-flated cushion membrane structures[J]. Journal of Harbin Institute of Technology, 2008, 40(12): 2020-2023. DOI:10.3321/j.issn:0367-6234.2008.12.036 |
| [17] |
YAN S W, CHEN J, SUN L Q. Methods for designing partially inflated geotubes[J]. Journal of Marine Science & Technology, 2016, 24(1): 1-9. |
 2018, Vol. 50
2018, Vol. 50


