砖砌体结构是用烧结黏土砖和砂浆砌筑而成的墙、柱作为建筑物主要受力构件的结构.砖砌体结构房屋历史悠久,其应用量大面广[1].由于砌体结构规范的修订,相关地区的砌体结构房屋不符合新规范的要求;因为施工质量问题,砖砌体结构房屋的承重墙体承载力达不到设计要求;砖砌体结构房屋的使用功能改变,承重砖砌体所受荷载可能增大;对原建筑在其上直接加层或在其室内加层,承重砖砌体所受荷载会增大;砖砌体结构房屋的承重砖砌体的承载力在使用过程中存在退化现象;“5.12”汶川地震过程中发现有砖砌体结构房屋楼层被压溃的现象,说明震中和近震区的承重砖砌体的竖向承载力没有经受住考验[2-5].由于存在上述诸多情况,因此需对承重砖砌体进行加固.
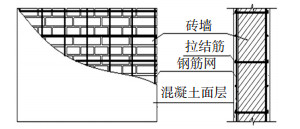
混凝土板墙加固是指在砖墙的一侧或两侧布置与砖墙有可靠拉结的钢筋网,并浇筑混凝土面层的加固方法,加固示意见图 1.
|
图 1 混凝土板墙加固砖墙示意 Figure 1 The sketch ofconcrete wall reinforcing brick wall |
混凝土板墙主要由两部分构成,钢筋网和混凝土面层.一般通过L形或S形拉结筋把钢筋网固定在砖墙侧面,单面加固时采用锚入砖墙的L形拉结筋,双面加固时采用贯穿砖墙的S形拉结筋.板墙可根据面层厚度、单双面加固和现场条件采用支模浇筑或喷射混凝土两种方式.
文献[6]在1966年塔什干地震后对大量严重受损的砌体房屋使用钢筋网水泥砂浆面层加固砌体方法进行加固; 文献[7]采用多种加固方案对砌体结构进行了加固研究,试验结果分析表明,采用混凝土板墙双面加固已损砌体的试验结果良好; 文献[8]研究了混凝土板墙加固砖墙的力学性能,文中采用喷射混凝土方法共进行了3个试件的试验,试验结果表明,双面加固墙体的性能优于单面加固的墙体; 文献[9]对16片采用钢筋网水泥砂浆面层加固混凝土砌体进行了试验研究,试验结果表明,采用钢筋网水泥砂浆面层对砖墙进行轴压加固是一种行之有效的方法; 文献[10]进行了88片混凝土板墙加固砖墙试验; 文献[11]进行了2片板墙加固砖墙试验; 文献[12]进行了6片板墙加固砖墙试验; 文献[13]进行了10片板墙加固砖墙试验,并提出了混凝土板墙加固砖墙的受剪承载力计算公式.众多国内外学者主要研究混凝土板墙加固砖墙的抗震性能及受剪承载力的计算.然而,对混凝土板墙加固砖墙的试验研究中都未考虑砖墙为在役情况,即未考虑原砖墙在加固前存在初始轴压力,对于混凝土板墙加固砖墙的轴心受压性能及轴压承载力计算的研究尚未见报道.事实上,混凝土达到峰值压应力时的压应变明显小于砖砌体达到峰值压应力时的压应变,由于原砖砌体存在初始压应力和初始压应变,加固后的砌体会在竖向荷载作用下出现板墙的钢筋混凝土面层被压坏后原砖墙才出现破坏的现象.这就存在当混凝土板墙加固砖墙达到轴压破坏时钢筋混凝土面层和原砖墙对竖向承载力的分担问题.因此,需对混凝土板墙加固砖墙的轴心受压性能及轴压承载力计算进行研究.
1 试件设计与制作 1.1 试件参数选取加固前原砖墙的试验轴压比取为0.15、0.25、0.35;高宽比取为0.8、1.1.原砖墙厚度取为120 mm;板墙中的钢筋网采用直径为8 mm的HRB335钢筋,横向和竖向钢筋间距均为150 mm.本次试验采用双面加固,每侧板墙厚度均为50 mm,混凝土采用C30普通混凝土.试验参数及配筋见表 1.
| 表 1 试件参数及配筋 Table 1 Test parameters and reinforcement |
烧结普通砖采用MU10,尺寸为240 mm×115 mm×53 mm.砌筑砂浆采用M10水泥砂浆.试验所用材料力学性能见表 2.
| 表 2 材料力学性能 Table 2 Mechanical properties of materials |
砖墙砌筑在底梁与顶梁之间.为通过张拉螺杆模拟砖墙的初始压力,在底梁制备时预埋钢筋以便后继与螺杆焊接,并在顶梁相同位置预留螺杆孔洞;为使板墙中的竖向钢筋在底梁和顶梁中的锚固满足要求,在底梁和顶梁处预埋和竖向钢筋相同间距、相同强度、相同直径的钢筋;为便于混凝土浇筑,在顶梁两侧各预留3个混凝土浇筑孔.底梁和顶梁按计算配筋,混凝土强度等级为C30.

|
图 2 底梁钢筋骨架 Figure 2 Ground beam steel skeleton |

|
图 3 底梁与顶梁浇筑成型 Figure 3 The ground beam and the top beam casting molding |
砖墙直接砌筑在底梁上.砖墙厚度为120 mm.由于是双面板墙加固,采用S形穿墙筋并按钢筋网交点位置预留在砖墙中,间距满足相应规范的要求,穿墙筋的预留见图 4.在砖墙表面中心区域粘贴应变片和安置竖向位移计,以便观测施加初始压力时砖墙的变形,见图 5.

|
图 4 砖墙中的穿墙筋 Figure 4 Rachel reinforcement in brick wall |

|
图 5 砖墙应变片及位移计 Figure 5 Theinstallation location of brick wall strain and displacement meter |
试验采用直径为20 mm的普通螺杆及其配套螺帽.将顶梁平放在砖墙顶部,为保证顶梁与砖墙接触均匀,在顶梁与砖墙间涂抹水泥砂浆,同时将螺杆同底梁预留钢筋焊接,待砂浆结硬后即可张拉螺杆.通过压力机对砖墙施加竖向荷载,并使用穿心式力传感器监测施力大小.通过砖墙上的应变片和位移计测得砖墙的初始压应变.

|
图 6 传感器监测施力大小 Figure 6 Testing through the wear heart type screw pull force sensor |

|
图 7 压力机施加压力 Figure 7 The process of pressuring |
通过底梁、顶梁中预埋的竖向钢筋和S形穿墙筋,将钢筋网固定在砖墙两侧,砖墙表面与钢筋网之间留有10 mm的空隙.在钢筋网的横向和竖向钢筋上粘贴应变片来考察钢筋在加载过程中应力的变化,见图 8.在顶梁的预留孔浇筑板墙的混凝土,混凝土中的骨料粒径满足相应要求.成形后的试件见图 9.

|
图 8 板墙中的钢筋网 Figure 8 Steel mesh in the brick wall |

|
图 9 成形后的试件 Figure 9 Specimens after demolding |
为了测定混凝土板墙加固砖墙在轴向压力作用下的力学性能,在混凝土面层的表面粘贴混凝土应变片及安置竖向位移计.由于砖墙表面已被混凝土面层包裹,在每个成形试件的两侧面,即砖墙的中间位置粘贴应变片,见图 10.为了保证粘贴的应变片不被破坏,把粘贴位置磨平后涂上AB胶找平,等AB胶干燥后,再用砂纸把AB胶磨平,然后再贴上应变片.在板墙混凝土面层上对应砖墙应变片的高度位置也粘贴应变片.通过在每片砖墙的两侧面和混凝土面层的相同高度位置粘贴应变片,来防止偏压造成的误差,板墙的应变片及位移计的粘贴位置见图 11.

|
图 10 砖墙粘贴应变片 Figure 10 Posting strain on the brick wall |

|
图 11 板墙安装应变片及位移计 Figure 11 Installing strain gauge and displacement meteron the concrete wall |
混凝土板墙加固砖墙轴压试验在5 000 kN压力试验机上进行.试验全貌见图 12.

|
图 12 混凝土板墙加固砖墙轴压试验 Figure 12 The test of brick wall strengthened with concrete splint |
SY-1:加载初期,试件处于弹性状态,即轴向荷载与轴向变形曲线呈直线.当轴向荷载达到1 707 kN时,板墙与砖墙间有局部出现分离;当轴向荷载达到2 032 kN时,板墙开始出现竖向裂缝,随着轴向荷载增大,裂缝数量开始增多,已有的裂缝长度不断发展,宽度逐渐增大;当轴向荷载达到2 710 kN时,板墙在中间部位向外侧鼓出,钢筋网中的竖向钢筋外露,砖墙在左右端部被压碎,试件破坏.
SY-2:加载初期,试件处于弹性状态.当轴向荷载达到1 947 kN时,板墙开始出现竖向裂缝;当轴向荷载达到2 089 kN时,板墙竖向裂缝增多;当轴向荷载到2 635 kN时,试件破坏.
SY-3:加载初期,试件处于弹性状态.当轴向荷载达到1 893 kN时,板墙与砖墙间有局部出现分离;当轴向荷载达到2 123 kN时,板墙出现竖向裂缝,随着轴向荷载增大,裂缝数量开始增多,已有的裂缝不断发展,板墙与砖墙局部分离加剧;当轴向荷载达到2 821 kN时,板墙混凝土被压碎,试件破坏.
SY-4:加载初期,试件处于弹性状态.当轴向荷载达到1 687 kN时,板墙与砖墙间有局部出现分离;当轴向荷载达到1 923 kN时,板墙开始出现竖向裂缝;当轴向荷载达到2 385 kN时,板墙向两侧鼓出,板墙中部出现了竖向裂缝,随着荷载的降低,砖墙被压碎.
SY-5:加载初期,试件处于弹性状态.当轴向荷载达到1 623 kN时,板墙出现竖向裂缝;当轴向荷载达到1 925 kN时,板墙竖向裂缝增多;当轴向荷载到2 321 kN时,混凝土板墙被压碎,随着荷载的不断下降,砖墙也被压碎.
SY-6:加载初期,试件处于弹性状态.当轴向荷载达到1 698 kN时,板墙出现竖向裂缝;当轴向荷载达到1 968 kN时,板墙竖向裂缝增多;当轴向荷载到2 424 kN时,板墙混凝土被压碎.随着荷载的降低,砖墙也随即被压碎.混凝土板墙加固砖墙试验的试件破坏情况见图 13.

|
图 13 混凝土板墙加固砖墙破坏情况 Figure 13 The damage of brick wall strengthened with concrete splint |
分析各个试件的破坏过程有以下共同特征:加载初期,试件处于弹性阶段,即轴向荷载与轴向变形曲线呈直线;随着竖向荷载的增加,板墙与砖墙分离并出现竖向裂缝,然后板墙中间部位外鼓、竖向钢筋外露,板墙混凝土压碎,最后砖墙破坏.
由6个加固墙片的试验现象和破坏情况得到如下两点认识:1)由于混凝土的泊松比比砖墙大,混凝土的横向变形理论上要大于砖墙,这样造成砖墙在横向受到混凝土的拉应力,因此随着混凝土变形的不断增大,砖墙竖向裂缝出现相对提前;2)在试验过程中出现板墙外鼓现象,提示穿墙筋的密度及其在板墙中的锚固长度应加密及加大.
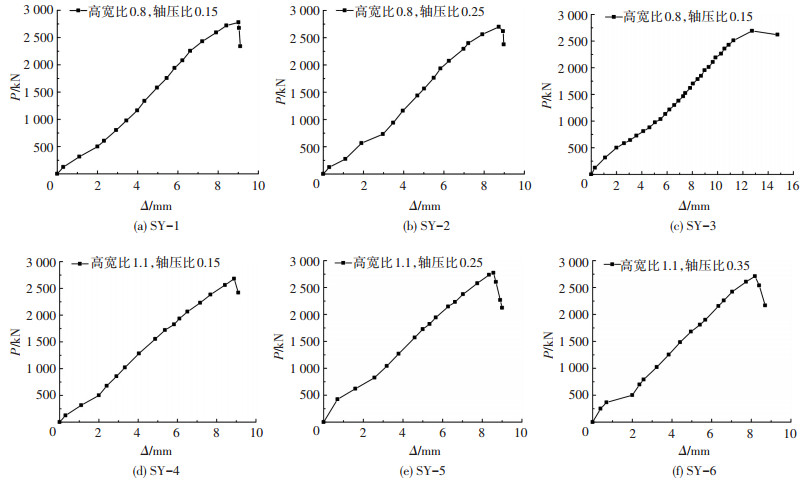
2.2 测试结果6个混凝土板墙加固砖墙试件的荷载-变形曲线见图 14,各墙体的极限荷载值见表 3.
|
图 14 墙体的荷载-位移曲线 Figure 14 The load-displacement curve of walls |
| 表 3 墙体的极限荷载 Table 3 The ultimate load of wall |
GB 50003—2011《砌体结构设计规范》给出了各类砌体抗压强度平均值的表达式:
| $ {f_{{\rm{w, m}}}} = {k_1}f_1^{\rm{a}}(1 + 0.07{f_2}){k_2}. $ | (1) |
式中:f1为砖块抗压强度平均值,即表 2中fzm,MPa; f2为砂浆抗压强度平均值,即表 2中fsm,MPa; fw, m为砖墙的抗压强度平均值,MPa; k1为与砖块类别及砌筑方法相关的参数,对烧结普通砖,可取0.78;k2为用低强度等级砂浆砌筑的砖墙强度修正系数,当f2 < 1.0时,k2=0.6+0.4f2,否则取1.0;a为与砌块高度相关的参数,烧结普通砖可取0.5.
本文采用文献[14]提出的式(2)所示的砖砌体受压应力-应变关系:
| $ \frac{\varepsilon }{{{\varepsilon _0}}} = \left\{ \begin{array}{l} \frac{{1.52\frac{\sigma }{{{\sigma _0}}}-0.279{{(\frac{\sigma }{{{\sigma _0}}})}^2}}}{{1-0.483\frac{\sigma }{{{\sigma _0}}} + 0.724{{(\frac{\sigma }{{{\sigma _0}}})}^2}}}, \;\;0 \le \frac{\sigma }{{{\sigma _0}}} \le 1;\\ \frac{{3.4\frac{\sigma }{{{\sigma _0}}}-1.13{{(\frac{\sigma }{{{\sigma _0}}})}^2}}}{{1 + 1.4\frac{\sigma }{{{\sigma _0}}} - 0.13{{(\frac{\sigma }{{{\sigma _0}}})}^2}}}, \;\;\;\;\;\;\;\frac{\sigma }{{{\sigma _0}}} \ge 1. \end{array} \right. $ | (2) |
式中:σ0为峰值应力,即式(1)中fw, m; ε0为峰值应力对应的应变.
砖砌体的弹性模量因应力、应变取值的不同而有几种不同的表达方法.但实际工程中一般取σ=0.43fw, m时的割线模量作为砌体的弹性模量[15]:
| $ E = 3.282\frac{{{f_{\rm{m}}}}}{{{\varepsilon _0}}}, $ | (3) |
砖墙的峰值压应变为
| $ {\varepsilon _0} = \frac{{3.28}}{{370\sqrt {{f_{{\rm{w, m}}}}} }}. $ | (4) |
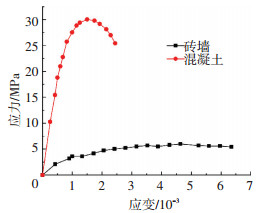
砖砌体泊松比介于0.14~0.16,可取为0.15.则砖墙、混凝土的受压应力-应变曲线见图 15;混凝土板墙加固砖墙中各材料力学性能指标见表 4.
|
图 15 砖墙和混凝土受压应力-应变曲线 Figure 15 The stress-strain curve of brick wall and concrete |
| 表 4 材料力学性能指标 Table 4 Mechanical properties of materials |
混凝土板墙加固砖墙后的墙体主要由两部分组成:原砖墙和后浇混凝土板墙.与普通构件不同,加固后墙体中的原砖墙属于二次受力构件,即加固前和加固过程中由原砖墙承受一部分荷载,后浇混凝土板墙在加固后才开始承担加固后新增加的部分荷载,因此后浇混凝土板墙应变滞后于原砖墙.当原砖墙达到极限压应变时,后浇混凝土板墙可能尚未达到峰值应力对应的压应变,或者当后浇混凝土板墙达到峰值应力对应的压应变时,原砖墙未达到峰值应力对应的压应变.因而加固后的砖墙承载力并不等于新旧两部分承载力的简单叠加.
从图 15和表 4中可以看出混凝土与砖墙的主要力学性能指标都大不相同,砖墙的峰值压应力对应的压应变远比混凝土的高,也就是说,混凝土首先破坏,然后是砖墙破坏.由于混凝土的泊松比高于砖墙,即在竖向相同的应变下,混凝土的横向变形大于砖墙的横向变形,因此使砖墙横向受拉破坏.混凝土和砖墙受压应力-应变关系见图 16.

|
图 16 混凝土和砖墙受压应力-应变关系 Figure 16 The stress-strain curve of concrete and brick wall |
图 16中σ1和ε1分别为加固前原砖墙的应力和应变值,该值取决于原砖墙在加固前的应力水平;加固后,混凝土在新增荷载的作用下开始受压变形,故混凝土的应变滞后于原砖墙.后浇混凝土板墙的应力-应变曲线从(ε1,0)开始,而此时砖墙的应变则是在前期累积变形ε1的基础上即在新增荷载作用下继续发展.
加固后墙体的极限竖向承载力由三部分组成:砖墙、板墙中的混凝土及板墙中的钢筋.混凝土板墙会首先达到峰值压应力对应的压应变而破坏,此时砖墙未达到峰值应变,但从试验现象来看,当混凝土板墙破坏后,砖墙即刻被压碎,故以混凝土达到峰值压应力时的压应变为三者破坏时的压应变.图 16中的εu为加固后墙体破坏时的压应变,把(εu-ε1)代入混凝土的应力-应变关系中即可求出对应于εu的应力σc,代入砖墙的应力-应变曲线中则可求出对应于εu的应力σm.因混凝土的峰值压应变小于砖墙的峰值压应变,故当混凝土达到峰值应力时,砖墙未达到峰值应力.钢筋屈服压应变小于混凝土峰值压应力对应的压应变,故沿墙高度方向布置的纵向钢筋以达到其抗压屈服强度来计算.
基于试验结果,引入砖墙和混凝土两种主要材料的强度利用系数αm和αc,混凝土板墙加固砖墙轴心受压承载力计算公式为
| $ N \le {\alpha _{\rm{m}}}{f_{{\rm{w, m}}}}{A_{\rm{m}}} + {\alpha _{\rm{c}}}{f_{{\rm{c, m}}}}{A_{\rm{c}}} + f{'_{{\rm{ym}}}}A{'_{\rm{s}}}. $ | (5) |
式中:fw, m为砖墙的抗压强度平均值,Am为砖墙的截面面积,Ac为混凝土板墙的截面总面积,αm为砖墙强度利用系数,与加固前应力水平有关,
该公式的适用条件为:试验轴压比为0.15~0.35,砖为MU10,砂浆为M10,砖墙高厚比为16~22.公式的试验轴压比适用范围为0.15~0.35,考虑到砖砌体抗压强度设计值为抗压强度实测平均值的0.45倍,砖砌体轴向压力设计值约为轴向压力实测值的1.32倍,砖砌体的总安全系数
| 表 5 混凝土板墙加固砖墙轴心受压承载力拟合结果 Table 5 The fitting results under axial compression of brick wall strengthened with concrete splint |
工程设计时,参照有关规范,恒荷载与活荷载构成的荷载效应的平均值一般为1.27,砖墙的分项系数为1.6,烧结普通砖砌筑的砖墙抗压强度变异系数为0.17,可以推出设计轴压比与试验轴压比的关系:
| $ \frac{{{\sigma _0}}}{{{f_{\rm{m}}}}} = \frac{{\sigma /1.27}}{{1.6f/(1-1.645 \times 0.17)}} = 0.355\frac{\sigma }{f}. $ | (6) |
同时,混凝土、钢筋、砖砌体的抗压强度均取设计值.
4 结论1) 提出了通过在砖墙底梁和顶梁间预拉螺杆模拟在役砖砌体结构房屋砖墙在进行混凝土板墙加固前初应力的方法.完成了高宽比分别为0.8和1.1,轴压比分别为0.15、0.25和0.35的6片混凝土板墙加固砖墙的轴心受压承载力试验,试验结果表明,混凝土板墙先于砖墙被压碎,加固后砖墙的轴压承载力明显提高.
2) 由于混凝土达到峰值压应力时对应的压应变明显低于砖墙达到峰值压应力时的压应变,同时由于穿墙筋在板墙混凝土中的锚固难以满足构造要求,不能对混凝土板墙提供可靠的拉锚,板墙加固砖墙不但混凝土板墙先于砖墙被压碎,而且二者不能充分发挥作用.基于试验结果,引入混凝土强度利用系数αc和砖墙强度利用系数αm,建立了混凝土板墙加固砖墙轴心受压承载力计算公式,并使试验值和计算值拟合较好.
| [1] |
NANNI A, TUMIALAN J. Fiber-reinforced composites for the strengthening of masonry structures[J]. Journal of the International Association for Bridge and Structural Engineering, 2003, 13(4): 271-278. |
| [2] |
清华大学土木结构组, 西南交通大学土木结构组, 北京交通大学土木结构组. 汶川地震建筑震害分析[J]. 建筑结构学报, 2008, 29(4): 1-9. Civil and Structural Groups of Tsinghua University, Xi'nan Jiaotong university, Beijing Jiaotong University. Analysis on seismic damage of building in the Wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(4): 1-9. DOI:10.14006/j.jzjgxb.2008.04.001 |
| [3] |
吴丽洁. 砖砌体结构房屋震害分析及设计建议[D]. 哈尔滨: 哈尔滨工业大学, 2010: 11-32. WU Lijie. Seismic damage analysis and design suggestions on brick masonry buildings[D]. Harbin: Master degree thesis of Harbin Institute of Technology, 2010: 11-32. |
| [4] |
李宏男, 肖诗云, 霍林生. 汶川地震震害调查与启示[J]. 建筑结构学报, 2008, 29(4): 10-19. LI Hongnan, XIAO Shiyun, HUO Linsheng. Damage investigation and analysis of engineering structures in the Wenchuan earthquake[J]. Journal of Building Structures, 2008, 29(4): 10-19. DOI:10.14006/j.jzjgxb.2008.04.002 |
| [5] |
王成. 玉树4.14地震建筑结构震害调查与分析[J]. 建筑结构, 2010, 40(8): 106-109. WANG Cheng. Investigation and analysis of building structure damage in Yushu Earthquake[J]. Journal of Building Structure, 2010, 40(8): 106-109. |
| [6] |
JABAROV M, KOZHARINOV S V, LUNYOV A. Strengthening of damaged masonry by reinforced mortar layers[C]//Proceedings of the 7th World Conference on Earthquake Engineering. Istanbul: [s. n. ], 1980, 15(3): 73-80.
|
| [7] |
KARANTONI F, FARDIS M. Effectiveness of seismic strenthening techniques for masonry buildings[J]. ASCE, 1992, 118(7): 1884-1902. DOI:10.1061/(ASCE)0733-9445(1992)118:7(1884) |
| [8] |
MELGAWADY M A, LESTUZZI P, BADOUX M. Retrofitting of masonry walls using shotcrete[C]//2006 NZSEE Conference. New Zealand: [s. n. ], 2006: 45-54.
|
| [9] |
OLIVEIRA F L, HANAI J B. Axial compression behavior of concrete masonry wallettes strengthenedwith cement mortar overlays[J]. Ibarcon Structures and Materials Journal, 2008, 1(2): 158-170. |
| [10] |
楼永林. 夹板墙的试验研究与加固设计[J]. 建筑结构学报, 1988(4): 1-12. LOU Yonglin. Research and design of strengthening brick walls by cement or reinforced cement mortar coatings[J]. Journal of Building Structures, 1988(4): 1-12. DOI:10.14006/j.jzjgxb.1988.04.001 |
| [11] |
苏三庆, 丰定国. 用夹板墙加固砖房的抗震性能[J]. 西安建筑科技大学学报, 1998, 30(3): 233-237. SU Sanqing, FENG Dingguo. Aseismic behavior of brick masonry building strengthened with steel-meshed cement mortar[J]. Journal of Xi'an University of Architecture&Technology, 1998, 30(3): 233-237. DOI:10.15986/j.1006-7930.1998.03.008 |
| [12] |
付洁, 王志浩. 自密实混凝土板墙加固低强度砂浆砖砌体的试验研究[J]. 建筑结构, 2007, 37(3): 49-52. FU Jie, WANG Zhihao. Experimental study on low strength brick masonry wall strengthened with self-compacting concrete wall[J]. Journal of Building Structures, 2007, 37(3): 49-52. |
| [13] |
黄世敏, 姚秋来, 康艳博. 混凝土板墙加固后墙片与剪力墙性能的对比研究[J]. 防灾减灾工程学报, 2011, 31(5): 567-571. HUANG Shimin, YAO Qiulai, KANG Yanbo. Comparative study on brick wall strengthened with concrete splint and shear wall[J]. Journal of Disaster Prevention and Mitigation Engineering, 2011, 31(5): 567-571. DOI:10.13409/j.cnki.jdpme.2011.05.014 |
| [14] |
庄一舟, 黄承逵. 模型砖砌体力学性能的试验研究[J]. 建筑结构, 1997(2): 22-25. ZHUANG Yizhou, HUANG Chengkui. Experimental study on mechanical properties of model brick masonry[J]. Journal of Building Structures, 1997(2): 22-25. |
| [15] |
刘桂秋, 施楚贤, 刘一彪. 砌体及砌体材料弹性模量取值的研究[J]. 湖南大学学报(自然科学版), 2008, 35(4): 29-32. LIU Guiqiu, SHI Chuxian, LIU Yibiao. Analyses of the elastic modulus values of masonry[J]. Journal of Hunan University (Natural Sciences), 2008, 35(4): 29-32. |
 2018, Vol. 50
2018, Vol. 50


