国家标准GB 50010—2010《混凝土结构设计规范》[1]纳入了HRB500钢筋,修订中的GB1499.2《钢筋混凝土用钢第二部分:热轧带肋钢筋》已考虑新增HRB600钢筋.高强钢筋具有更高屈服强度的特点,给工程带来诸多益处[2],但也使得其在混凝土中所需要的锚固长度进一步增大.当锚固长度不宜过长时,GB 50010—2010《混凝土结构设计规范》中规定了可在钢筋末端采用弯钩或机械锚固的措施来减小锚固长度.在钢筋末端连接锚固板就是一种常见的机械锚固形式.
文献[3]完成了4组共计72个拉拔试件的试验.试验分析了不同混凝土强度(C20、C30和C40)、不同钢筋公称直径d(8、12、18、25 mm)、不同保护层厚度c(37.5、41、44、46 mm)、不同埋置长度(10d、12d和15d)和不同配箍率对直锚高强钢筋黏结力的影响,验证了HRB500钢筋的极限黏结强度、黏结-滑移本构关系均符合中国黏结锚固专题研究组所提出的计算方法[4],这为带锚固板钢筋受力问题的程序计算提供了基础.
文献[5]通过完成36个带锚固板和36个带加焊筋的HRB500的拉拔件试验,对中国黏结锚固专题研究组提出的黏结强度计算公式进行了修正.通过对不同钢筋公称直径d(12、16、25 mm)、不同钢筋埋置长度lat(10d和15d)、不同配箍率ρsv(0.43%、0.66%和0.88%)、不同混凝土强度(C40、C50和C70)、不同保护层厚度c(1d和2d)、不同锚固板净面积(锚固钢筋公称面积的4.5~5.0倍)和双侧焊筋不同长度(30 mm和50 mm)的分析,拟合得到了锚固板承压作用折算的锚固强度τua和直锚段黏结作用折算的锚固强度τum两部分计算公式:
| $ {\tau _{{\rm{ua}}}} = 0.583\left( {0.82 + 0.9\frac{d}{{{l_{{\rm{at}}}}}}} \right)\left( {1.6 + 0.7\frac{c}{d} + 20{\rho _{{\rm{sv}}}}} \right){f_{\rm{t}}}, $ |
| $ {\tau _{{\rm{um}}}} = 81.237{f_{\rm{t}}}d/\left( {{\rm{ \mathsf{ π} }}{l_{{\rm{at}}}}} \right), $ |
进而可以得到机械锚固黏结强度τu=τua+τum.这两个公式均由两种机械锚固形式的结果共同回归得到,可以为计算钢筋机械锚固力问题提供一定的依据.但是,双侧焊筋锚固与端部焊锚板锚固的受力特点和破坏机理都有所差异,以一种统一的公式来计算锚固力,会造成一定的误差.
文献[6]完成了70个采用HRC公司钢筋锚固板产品(钢筋直径约25 mm,锚固板尺寸约75 mm×75 mm)的混凝土梁式拉拔试验.给出了该钢筋锚固板产品的锚固长度计算公式:
| $ {l_{{\rm{at}}}} = \frac{{22d{f_{\rm{y}}}}}{{60\sqrt {{{f'}_{\rm{c}}}} }}\left( {\frac{{3d}}{{c + {K_{{\rm{tr}}}}}}} \right)\left( {\alpha \beta \gamma \psi } \right),{K_{{\rm{tr}}}} = \frac{{{A_{{\rm{tr}}}}{f_{{\rm{yt}}}}}}{{1500sn}}. $ |
式中:fy为钢筋屈服强度,fc'为混凝土圆柱体抗压强度,c为混凝土保护层厚度,Ktr为横向配筋指标,s为锚固长度范围内的横向钢筋最大中心距离,n为开裂面上的钢筋数,fyt为横向钢筋的屈服强度,Atr为锚固长度范围内开裂面上的横向钢筋面积.α、β、γ、ψ是建议考虑浇筑方式、轻质骨料、环氧树脂和锚固长度范围内超筋的影响.但是,在公式应用时,需要满足试件保护层厚度大于3倍钢筋公称直径、锚固板承压面积与锚固钢筋公称面积比值约9、锚固长度最小值不小于6倍钢筋公称直径或150 mm等限制条件,因此在适用范围上存在着局限性.
文献[7-8]进行了2个中间层边节点和3个顶层边节点的试验.其中,中间层边节点中受力钢筋公称直径为25 mm,锚固板承压面积约为4倍锚固钢筋公称面积;顶层边节点中受力钢筋公称直径为16 mm和20 mm,锚固板尺寸为边长50 mm的正方形.试验结果表明,带锚固板钢筋的节点受力性能可以满足美国规范对房屋节点的要求,并给出了受力钢筋公称直径为16~25 mm的锚固长度不小于12倍钢筋公称直径,锚固板承压面积不小于4倍锚固钢筋公称面积的建议.
美国混凝土建筑规范ACI318-2014中规定[9],带锚固板变形钢筋锚固长度lat为
| $ {l_{{\rm{at}}}} = \left( {0.016{\psi _{\rm{e}}}\frac{{{f_{\rm{y}}}}}{{\sqrt {{{f'}_{\rm{c}}}} }}} \right)d. $ |
式中:fc'为混凝土圆柱体抗压强度;ψe为环氧涂层的影响系数,采用环氧涂层时取为1.2,其余取为1.0;fy为钢筋屈服强度.另外,lat长度不得少于8d或150 mm中的较大值.另外,规范中也给出了变形钢筋屈服强度不超过420 MPa、混凝土强度等级不超过40 MPa、钢筋公称直径d不得超过36 mm、锚固板净承压面积不少于4倍锚固钢筋公称面积、保护层厚度不小于2d、相邻钢筋净距不小于4d的公式限制条件.
国家行业标准JGJ 256—2011《钢筋锚固板应用技术规程》[10]中也对部分锚固板给出了类似规定:承压面积不应小于锚固钢筋公称面积的4.5倍;钢筋公称直径不宜大于40 mm;钢筋屈服强度为335、400、500 MPa时,对应混凝土强度等级不低于C30、C35、C40;锚固长度不应低于0.3lab.
以往的研究成果及各国规范,基本上都是通过限制锚固板承压面面积与锚固钢筋公称面积比值下限和钢筋直锚段长度下限来保障带锚固板钢筋的可靠锚固,这样可能会造成直锚段过长或者锚固板过大.因此,合理考虑钢筋公称直径、钢筋屈服强度、混凝土强度、钢筋埋置长度等因素的影响,给出锚固力在直锚段钢筋黏结和锚固板承压间分配规律的具体算法,能够更准确地给出钢筋锚固长度和锚固板尺寸,把带锚固板钢筋在锚固问题上的被动校核转变为主动选择,具有一定的工程使用价值与意义.
1 钢筋锚固数值分析 1.1 本构模型变形钢筋黏结-滑移本构关系采用文献[11-13]的研究成果.该本构关系以黏结应力-滑移基本关系Φ(s)与位置函数ψ(x)的乘积形式,表示出锚固长度范围内每一个点的局部黏结应力-滑移关系.
τ-s基本关系曲线上4个黏结锚固特征强度表达式为:
滑移强度:
| $ {\tau _{\rm{s}}} = 0.99{f_{\rm{t}}}, $ |
劈裂强度:
| $ {\tau _{{\rm{cr}}}} = \left( {1.6 + 0.7\frac{c}{d}} \right){f_{\rm{t}}}, $ |
极限强度:
| $ {\tau _{\rm{u}}} = \left( {1.6 + 0.7\frac{c}{d} + 20{\rho _{{\rm{sv}}}}} \right){f_{\rm{t}}}, $ |
残余强度:
| $ {\tau _{\rm{r}}} = 0.98{f_{\rm{t}}}. $ |
式中:ft为混凝土抗拉强度,MPa;c为混凝土表面到纵向受力钢筋外边缘的距离,mm;d为钢筋公称直径,mm;ρsv为配箍率.此外,相应的特征滑移值分别为ss=0.000 8d,scr=0.024 0d,su=0.036 8d,sr=0.540 0d.
位置函数表达式为
| $ \psi \left( x \right) = \left[ {1 + {{\left( {\frac{x}{{{l_{{\rm{at}}}}}}} \right)}^4}} \right]\sin \frac{x}{{{l_{{\rm{at}}}}}}{\rm{ \mathsf{ π} }}, $ |
式中:lat为钢筋直锚段长度,x为钢筋直锚段上一点距自由端的长度.
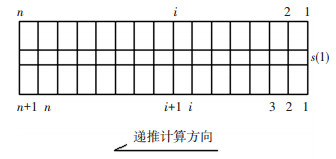
1.2 数值分析方法将埋置长度lat平均划分为n个单元(见图 1),每个单元长度Δx=lat/n.若在加载端施加滑移sl,则将引起锚固长度范围内各单元相关变量的变化.利用下列递推关系式可进行递推计算:
| $ {\sigma _{\rm{s}}}\left( {i + 1} \right) = {\sigma _{\rm{s}}}\left( i \right) - \frac{{4\tau \left( i \right)}}{d}\Delta x, $ |
| $ {\sigma _{\rm{c}}}\left( {i + 1} \right) = {\sigma _{\rm{c}}}\left( i \right) - \left[ {{\sigma _{\rm{s}}}\left( i \right) - {\sigma _{\rm{s}}}\left( {i + 1} \right)} \right]\frac{{{A_{\rm{s}}}}}{{{A_{\rm{c}}}}}. $ |
|
图 1 单元划分和递推计算 Figure 1 The method of division and calculation |
式中:As为受力纵筋横截面积,Ac为混凝土受力影响区的横截面积.由本构关系可计算钢筋应变εs(i)和混凝土应变εc(i),并由应变差递推下一单元的滑移s(i+1).
| $ \begin{array}{l} s\left( {i + 1} \right) = s\left( i \right) - \left[ {\frac{{{\varepsilon _{\rm{s}}}\left( i \right) + {\varepsilon _{\rm{s}}}\left( {i + 1} \right)}}{2} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{\gamma _{\rm{c}}}\frac{{{\varepsilon _{\rm{c}}}\left( i \right) + {\varepsilon _{\rm{c}}}\left( {i + 1} \right)}}{2}} \right]\Delta x, \end{array} $ |
式中γc为混凝土应变不均匀系数,本文按徐有邻教授建议取2.由s(i+1)根据τ-s本构关系求得下一单元的黏结应力τ(i+1).依次递推,直到算至最后一个单元或递推至某一单元时,钢筋应力和滑移在误差允许范围内满足边界条件.
在计算带锚固板钢筋直锚段的黏结作用时,认为锚固板承压面处钢筋的滑移值为0,并且钢筋埋置长度lat已知,因此自由端的边界条件为s(lat)=0,σs(lat)=Fp(Fp为锚固板承压作用力).在加载端钢筋应力给定的条件下,通过调整加载端滑移sl,使递推计算结果满足边界条件.由此可以得到加载端钢筋任一应力下,带锚固板钢筋直锚段黏结作用的分布情况.
将加载端钢筋屈服而自由端钢筋不发生滑移时的最小锚固长度,定义为受拉钢筋的稳定锚固长度las.由稳定锚固长度las的定义可以得到新的边界条件,σs(0)=fy、σs(lat)=0、s(lat)=0.由于钢筋埋置长度lat和加载端滑移sl均为迭代自变量,所以先假设一个lat,按计算带锚固板钢筋直锚段黏结作用的方法进行迭代计算,对迭代结果进行判断来调整所假设的lat,直至计算结果满足边界条件,所得到的长度即为稳定锚固长度las.
2 数值分析与试验结果对比试验完成了共计120个中心埋置单根带锚固板高强钢筋混凝土试件的拉拔试验.钢筋采用HRB500和HRB600两种,公称直径分别为20 mm、22 mm和25 mm三种.每种钢筋各截取3个试样,试样长度为600 mm,并根据GB/T 228.1—2010《金属材料拉伸试验第1部分:室温试验方法》[14]的规定进行钢筋材性试验.当钢筋采用HRB500时,混凝土采用C30~C60四种强度等级;而当钢筋采用HRB600时,混凝土则采用C40~C70四种强度等级.纵向钢筋埋置长度lat是同等条件下钢筋临界锚固长度lac的0.3~0.7倍.混凝土拉拔试件的横截面尺寸统一为150 mm×150 mm.钢筋与混凝土力学性能见表 1、2.
| 表 1 钢筋材料力学性能 Table 1 Mechanical properties of reinforcement bars |
| 表 2 混凝土材料力学性能 Table 2 Mechanical properties of concrete |
为尽量不改变钢筋表面形状,沿钢筋纵肋一侧开4 mm×4 mm槽口,槽口紧贴钢筋纵肋边缘,钢筋埋置长度范围内每30 mm在槽底布置一个1 mm×2 mm应变片,先后涂抹氯丁胶、植筋胶封槽.应变片的布置及后处理见图 2.

|
图 2 应变片的布置及处理 Figure 2 Processing the strain gauges |
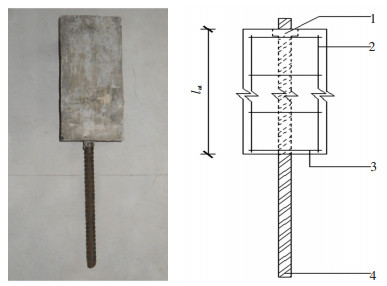
混凝土拉拔件配置4Φ8纵筋(HPB300),用于固定箍筋.箍筋选用HPB300钢筋,公称直径为8 mm,间距为100 mm.20、22、25 mm三种公称直径的钢筋末端锚板尺寸分别为40 mm×40 mm、45 mm× 45 mm和50 mm×50 mm,钢板厚度均为16 mm,末端锚固板与钢筋通过穿孔塞焊.混凝土拉拔试件示意见图 3,其中,1为钢筋锚固板,2为架立筋,3为箍筋,4为受拉纵筋.
|
图 3 拉拔试件示意 Figure 3 The pull-out specimen |
试件拉拔力由荷载采集系统采集,沿钢筋纵肋所开槽内的应变片读数随荷载的变化用DH3816静态应变采集仪采集.由于混凝土拉拔试件的锚固力T由直锚段钢筋黏结力Fb与锚固板承压力Fp共同承担,因此通过应变片的实测值,可以获得在各级荷载作用下真实的钢筋黏结力Fbt与真实的锚固板承压力Fpt.借助MATLAB数值分析程序,可以得到各试件在各级荷载下的直锚段钢筋黏结力Fbc与锚固板承压力Fpc.表 3给出了钢筋屈服时刻,计算的锚固板承压力Fpc与真实的锚固板承压力Fpt.
| 表 3 Fpt值与Fpc值 Table 3 Values of Fpt and Fpc |
经计算,表 3中各个试件计算的锚固板承压力Fpc与真实的锚固板承压力Fpt的比值平均值为1.00,标准差为0.07,变异系数为0.07.对比结果表明,程序计算的结果具有较高精度,可利用程序对锚固力在钢筋直锚段黏结力与锚固板承压力之间的分配问题进行分析.
3 影响因素分析为方便分析,将混凝土拉拔试件的锚固力T、直锚段钢筋黏结力Fb和锚固板承压力Fp都分别除以钢筋横截面积,以应力形式表达:
| $ {f_{\rm{T}}} = {f_{\rm{b}}} + {f_{\rm{p}}}. $ |
式中:fT为钢筋加载端应力,MPa;fb为直锚段钢筋黏结应力,MPa;fp为锚固板承压应力,MPa.
参考以往学者对直锚钢筋黏结力的分析成果[15],也同样将钢筋埋置长度lat和混凝土保护层厚度c分别除以钢筋公称直径d进行无量纲化处理.通过分别改变混凝土拉拔试件受力纵筋屈服强度fy、混凝土强度等级、混凝土相对保护层厚度c/d、钢筋相对埋置长度lat/d等参数,分析各参数对直锚段钢筋黏结应力fb的影响,从而揭示锚固力在钢筋直锚段黏结力与锚固板承压力之间的分配关系.在进行程序分析时,钢筋屈服强度fy统一取为钢筋屈服强度标准值的1.1倍,即HRB500级钢筋屈服强度取为550 MPa,HRB600级钢筋屈服强度取为660 MPa.混凝土力学性能则按照表 2进行选取.
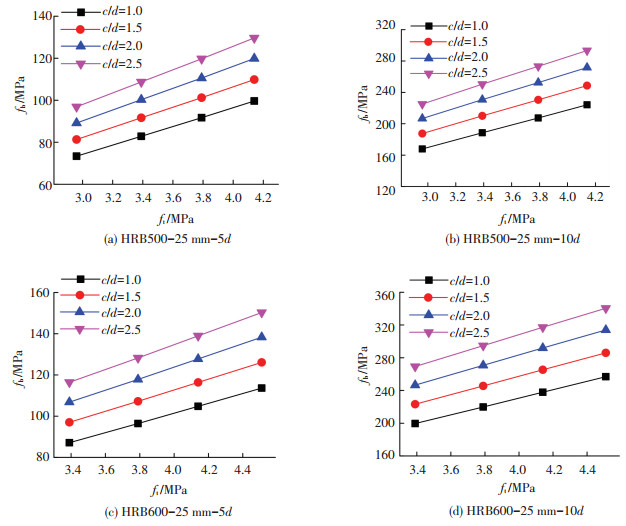
3.1 混凝土强度的影响混凝土的强度是影响钢筋与混凝土间黏结强度的重要因素,不论是化学胶结力、摩擦力还是机械咬合力都与其相关[16].在钢筋屈服强度fy、钢筋相对埋置长度lat/d和混凝土相对保护层厚度c/d相同的条件下,分析混凝土强度对直锚段钢筋黏结应力fb的影响.通过对混凝土抗压强度fc与抗拉强度ft的分析,发现拉拔试件加载端钢筋达到屈服时刻,fb随ft的变化趋势更接近线性.图 4分别给出了HRB500或HRB600钢筋、钢筋公称直径25 mm、埋置长度5d或10d、不同c/d(范围在1.0~2.5)时,fb随ft的变化规律.
|
图 4 ft对fb的影响 Figure 4 The effect of ft on fb |
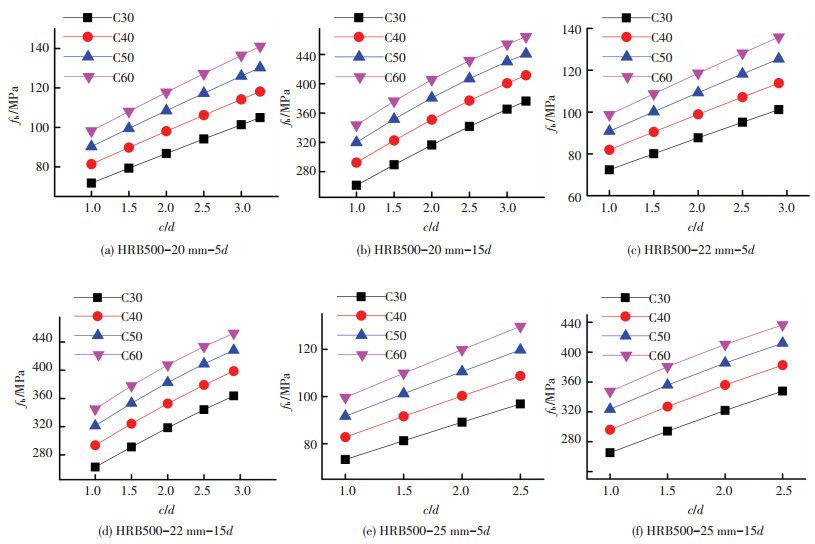
本文所指的保护层厚度为纵向受力钢筋外边缘到混凝土表面的距离,而不是箍筋外边缘到混凝土表面的距离.在钢筋屈服强度fy、钢筋相对埋置长度lat/d和混凝土抗拉强度ft相同的条件下,分析混凝土相对保护层厚度c/d对直锚段钢筋黏结应力fb的影响.图 5分别给出了HRB500钢筋、不同钢筋公称直径(20、22和25 mm)、不同混凝土强度(C30、C40、C50和C60)、不同钢筋埋置长度(5d和15d)情况下,fb随c/d的变化规律.
|
图 5 HRB500时c/d对fb的影响 Figure 5 The effect of c/d on fb with HRB500 |
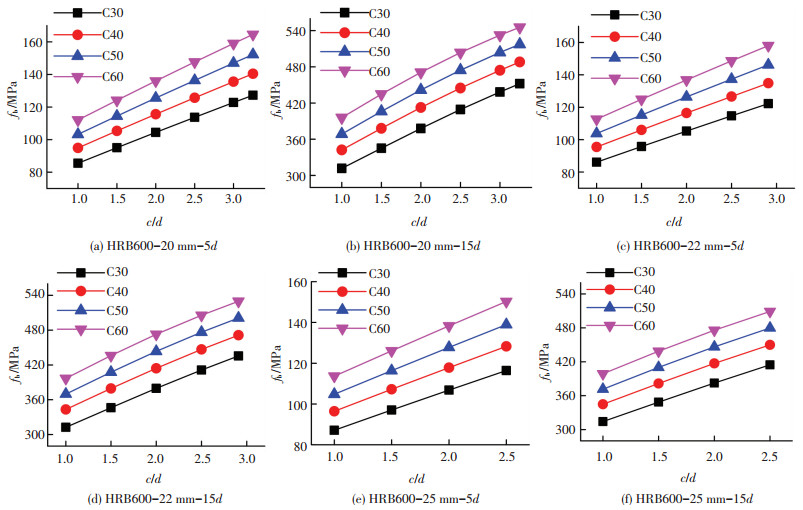
图 6分别给出了HRB600钢筋、不同钢筋公称直径(20、22和25 mm)、不同混凝土强度(C40、C50、C60和C70)、不同钢筋埋置长度(5d和15d)情况下,fb随c/d的变化规律.
|
图 6 HRB600时c/d对fb的影响 Figure 6 The effect of c/d on fb with HRB600 |
由图 5、6可知,当钢筋屈服强度fy、钢筋相对埋置长度lat/d和混凝土抗拉强度ft一定时,加载端钢筋达到屈服时刻,直锚段钢筋的黏结应力fb随相对保护层厚度c/d的增大而增大.并且,当埋置长度较短(如埋置长度为5d)时,增长趋势为线性;当埋置长度较长(如埋置长度为15d)时,增长趋势表现出非线性的特征.
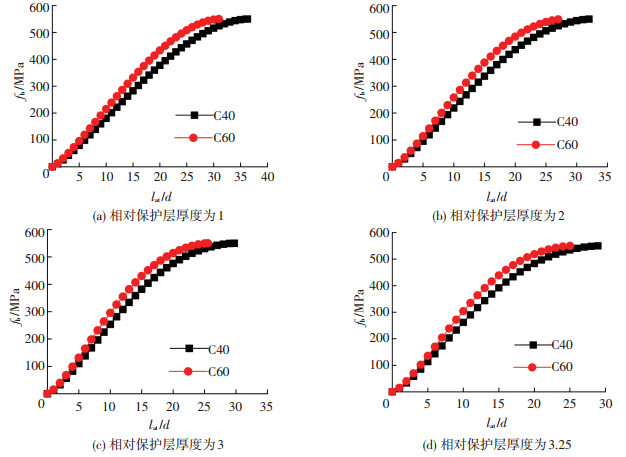
3.3 相对埋置长度lat/d的影响在钢筋屈服强度fy、混凝土抗拉强度ft和混凝土相对保护层厚度c/d相同的条件下,分析埋置长度lat/d对直锚段钢筋黏结应力fb的影响.因为稳定锚固长度las是加载端钢筋屈服时刻,锚固板进入工作状态的一个临界锚固长度.所以,本文研究的埋置长度范围最大值为相同条件下的稳定锚固长度las.图 7分别给出了公称直径20 mm的HRB500钢筋在C40或C60、不同相对保护层厚度时,fb随lat/d的变化规律.
|
图 7 lat/d对fb的影响 Figure 7 The effect of lat/d on fb |
由图 7可知,当钢筋屈服强度fy、混凝土相对保护层厚度c/d和混凝土轴心抗拉强度ft一定时,直锚段钢筋的黏结应力fb随钢筋相对埋置长度lat/d的增大而增大,但呈现出明显的非线性趋势.
4 稳定锚固长度的计算由前文可知,钢筋的稳定锚固长度las是一个重要的指标.稳定锚固长度是加载端钢筋达到屈服时刻,锚固板承压作用是否分担锚固力的一个界限锚固长度.当lat<las时,受拉钢筋的锚固力才由直锚段钢筋黏结作用和锚固板承压作用共同承担.通过数值分析发现,相对保护层厚度c/d和钢筋屈服强度与混凝土抗拉强度之比fy/ft,都对钢筋稳定锚固长度与钢筋公称直径之比las/d有一定影响.
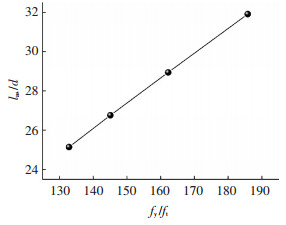
4.1 fy/ft对las/d的影响当选取HRB500钢筋,公称直径为20 mm,混凝土相对保护层厚度c/d为3.25时,分析了不同混凝土强度(C30、C40、C50和C60)条件下,fy/ft对las/d的影响.图 8给出了las/d随fy/ft的变化图,由图 8可知,las/d随fy/ft的增大而增大,且近似呈现线性关系.
|
图 8 fy/ft对las/d的影响 Figure 8 The effect of fy/ft on las/d |
当选取HRB600钢筋,公称直径为20 mm,混凝土强度为C40时,分析了不同混凝土相对保护层厚度(1.0、1.5、2.0、2.5、3.0和3.25)条件下,c/d对las/d的影响.图 9给出了las/d随c/d的变化图,由图 9可知,las/d随c/d的增大而减小,且呈现非线性关系.
由上述分析可得到,las/d随fy/ft的增大而线性增大,随c/d的增大而非线性减小.因此,通过以fy/ft与c/d为自变量,拟合得到las/d值的公式:
| $ {l_{{\rm{as}}}}/d = - 0.22\frac{{{f_{\rm{y}}}}}{{{f_{\rm{t}}}}} \cdot \frac{c}{d} + 0.16\frac{{{f_{\rm{y}}}}}{{{f_{\rm{t}}}}} + 0.31\frac{c}{d} + 12.34. $ |

|
图 9 c/d对las/d的影响 Figure 9 The effect of c/d on las/d |
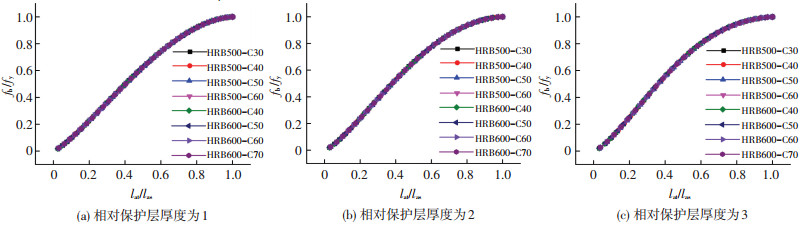
通过进一步的分析发现,钢筋屈服时刻,直锚段钢筋的黏结应力fb与钢筋屈服强度(总锚固力)fy之比fb/fy随钢筋埋置长度lat与稳定锚固长度las之比lat/las的变化趋势只与混凝土相对保护层厚度c/d有关.即当相对保护层厚度一定时,fb/fy随lat/las的变化规律是固定不变的.图 10分别给出了混凝土相对保护层厚度c/d取为1、2和3时,fb/fy随lat/las的变化规律.
|
图 10 c/d相同时fb/fy随lat/las的变化规律 Figure 10 The effect of fb/fy on lat/las with same c/d |
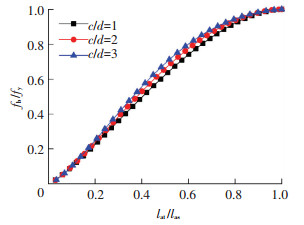
而当相对保护层厚度不同时,fb/fy随lat/las的变化规律有所不同,见图 11.通过对图 11中数据点的拟合,给出了fb/fy随lat/las变化规律的公式:
| $ \frac{{{f_{\rm{b}}}}}{{{f_{\rm{y}}}}} = {a_0} + {a_1}\cos \left( {w\frac{{{l_{{\rm{at}}}}}}{{{l_{{\rm{as}}}}}}} \right) + {b_1}\sin \left( {w\frac{{{l_{{\rm{at}}}}}}{{{l_{{\rm{as}}}}}}} \right),0 \le \frac{{{l_{{\rm{at}}}}}}{{{l_{{\rm{as}}}}}} \le 1. $ |
|
图 11 c/d不同时fb/fy随lat/las的变化规律 Figure 11 The effect of fb/fy on lat/las with different c/d |
式中的a0、a1、b1、w是与相对保护层厚度c/d有关的系数,其计算公式为:
| $ {a_0} = - 0.0556\frac{c}{d} + 0.432, $ |
| $ {a_1} = 0.0438\frac{c}{d} - 0.434, $ |
| $ {b_1} = 0.0861\frac{c}{d} + 0.405, $ |
| $ w = - 0.0115{\left( {\frac{c}{d}} \right)^2} + 0.0065\frac{c}{d} + 2.163. $ |
在给定钢筋屈服强度fy、混凝土抗拉强度ft、钢筋公称直径d、混凝土保护层厚度c、钢筋埋置长度lat等参数的条件下,根据以上公式就可以计算出加载端钢筋应力达到屈服强度时,直锚段钢筋的黏结应力fb与锚固板承压应力fp,从而确定钢筋锚固力在黏结作用和承压作用间的分配.
6 结论1) 通过对C30~C70混凝土、HRB500和HRB600钢筋和埋置长度0.3~0.7倍临界锚固长度的120个混凝土试件的拉拔试验,验证了基于受拉钢筋与混凝土间的黏结-滑移本构关系编写的程序计算结果的准确性,证明了利用程序进行带锚固板钢筋锚固力分配规律研究的可行性.
2) 提出了钢筋稳定锚固长度的概念,稳定锚固长度是指加载端钢筋应力达到屈服强度时,自由端钢筋与混凝土间不发生相对滑移的最小锚固长度,是锚固板是否进入工作的临界状态.分析表明las/d随fy/ft的增大而线性增大,随c/d的增大而非线性减小,建立了以fy/ft和c/d为自变量的las/d计算公式.
3) 通过分析加载端钢筋屈服时刻,各个参量对直锚段钢筋黏结应力fb的影响,发现带锚固板钢筋直锚段的黏结应力与钢筋屈服强度(总锚固力)fy之比fb/fy随带锚固板钢筋直锚段埋置长度与稳定锚固长度之比lat/las变化的规律只与相对保护层厚度c/d有关.并在此基础上结合稳定锚固长度的算法,建立了计算加载端钢筋应力达到屈服强度时刻直锚段钢筋黏结力公式.
| [1] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [2] |
李智斌. 带锚固板钢筋机械锚固性能的试验研究[D]. 天津: 天津大学, 2005. LI Zhibin. Experiment study in anchorage behavior of headed reinforcement[D]. Tianjin: Tianjin University, 2005. |
| [3] |
毛达岭. HRB500钢筋粘结锚固性能试验研究[D]. 天津: 天津大学, 2004.
|
| [4] |
汪洪, 徐有邻, 史志华. 钢筋机械锚固性能的试验研究[J]. 工业建筑, 1991(11): 36-40. WANG Hong, XU Youlin, SHI Zhihua. Experiment research of mechanical anchorage properties of bars in concrete[J]. Industrial Construction, 1991(11): 36-40. DOI:10.13204/j.gyjz1991.11.007 |
| [5] |
王莉荔. 500MPa级热轧带肋钢筋机械锚固性能试验研究[D]. 郑州: 郑州大学, 2010. WANG Lili. Experimental research on mechanical anchorage capability of HRB500 steel bar[D]. Zhengzhou: Zhengzhou University, 2010. |
| [6] |
THOMPSON M K, JIRSA J O, BREEN J E, et al. Anchorage behavior of headed reinforcement: literature review [R]. Austin, Texas: Center for Transportation Research Report 1855-1, 2002.
|
| [7] |
WALLACE J W, MCCONNELL S W, GUPTA P, et al. Use of headed reinforcement in beam-column joints subjected to earthquake loads[J]. ACI Structural Journal, 1998, 95(5): 590-606. |
| [8] |
WALLACE J W. Headed reinforcement a viable option[J]. Concrete International, 1997, 19(12): 47-53. |
| [9] |
American Concrete Institute. ACI committee 318 building code requirements for structural concrete: ACI 318-14 [S]. Farmington Hill, MI: American Concrete Institute, 2014.
|
| [10] |
钢筋锚固板应用技术规程: JGJ 256—2011[S]. 北京: 中国建筑工业出版社, 2011. Technical specification for application of headed bars: JGJ 256—2011[S]. Beijing: China Architecture & Building Press, 2010. |
| [11] |
徐有邻. 钢筋与混凝土粘结锚固的分析研究[J]. 建筑科学, 1992(4): 18-24. XU Youlin. Analytical study on bond-anchorage between bar and concrete[J]. Building Science, 1992(4): 18-24. DOI:10.13614/j.cnki.11-1962/tu.1992.04.003 |
| [12] |
徐有邻. 变形钢筋-混凝土粘结锚固性能的试验研究[D]. 北京: 清华大学, 1990.
|
| [13] |
徐有邻. 钢筋混凝土粘结滑移本构关系的简化模型[J]. 工程力学, 1997, 增刊: 34-38. |
| [14] |
金属材料拉伸试验第1部分: 室温试验方法: GB/T 228. 1—2010[S]. 北京: 中国标准出版社, 2011. Metallic materials-tensile testing-part 1: method of test at room temperature: GB/T 228. 1—2010[S]. Beijing: Standards Press of China, 2011. |
| [15] |
徐有邻, 汪洪, 史志华. 钢筋粘结锚固机理的试验研究[C]//混凝土结构基本理论及应用第二届学术讨论会论文集(第一卷). 北京: [s. n. ], 1990: 211-218.
|
| [16] |
徐有邻, 邵卓民, 沈文都. 钢筋与混凝土的粘结锚固强度[J]. 建筑科学, 1988(4): 8-14. XU Youlin, SHAO Zhuomin, SHEN Wendu. Bond strength between reinforcement bars and concrete[J]. Building Science, 1988(4): 8-14. |
 2018, Vol. 50
2018, Vol. 50


