2. 先进土木工程材料教育部重点实验室(同济大学),上海 200092
2. Key Laboratory of Advanced Civil Engineering Materials (Tongji University), Ministry of Education, Shanghai 200092, China
预应力型钢混凝土(PSRC)结构在普通型钢混凝土(SRC)中施加预应力,可有效改善SRC结构使用阶段工作性能.这种结构形式具有承载力高、刚度大、截面高度小、抗裂及变形性能好等优势.在中国,一些学者对PSRC结构开展相关研究,并取得了一定的成果[1-6].近年来,又有学者将高强混凝土(> C60)应用于PSRC结构,并进行了系列试验研究[7-9].
高强混凝土的应用可充分发挥PSRC结构承载力高、截面高度小的优势.然而,高强混凝土具有显著的脆性破坏特性[10].这可能会削弱构件或结构的整体延性.文献[9]对预应力型钢高强混凝土(PSRHC)梁的延性进行了研究,并提出了以综合配筋指标为变量的延性系数计算公式.虽然,综合配筋指标可集中反映配筋、材性等参数对截面变形能力的影响.但其忽视了箍筋约束作用的影响.研究表明,梁、柱构件中分布的箍筋同样会影响其延性[11].文献[12]在研究高强箍筋下高强混凝土圆柱延性时,便将箍筋的影响引入了其位移延性系数计算公式中.另外,当前仅有少量学者对PSRHC结构进行研究,相关试验样本较少.故需要合适的数值模拟方法来拓展对PSRHC结构的研究.
本文结合已有的试验研究成果,建立了基于纤维模型的PSRHC简支梁的数值模拟方法,引入约束混凝土本构间接考虑箍筋的约束作用;基于数值模型进行了参数分析,研究了混凝土强度等级、普通受拉、受压钢筋用量、预应力筋用量、型钢翼缘、腹板厚度、箍筋直径及间距等设计参数对延性的影响;结合截面应力分析及数值回归方法,建立了考虑箍筋影响的延性系数计算公式,可用于设计阶段PSRHC试件的延性评估.
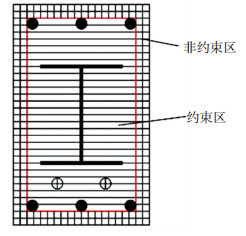
1 数值模拟 1.1 截面M-φ关系曲线计算采用纤维模型分析PSRC截面时,可将混凝土部分划分为两个区域[13]:1)非约束区,即箍筋外侧混凝土保护层;2)约束区,考虑箍筋约束作用(图 1).
|
图 1 截面纤维及区域划分 Figure 1 Division of section fiber and concrete zone |
分析受弯截面时,先确定截面曲率φ值,假定截面中心应变ε,然后可根据平截面假定计算任意纤维单元的应变:
| $ {\varepsilon _i} = \bar \varepsilon - {Z_i}\varphi , $ | (1) |
式中Zi为各纤维中心至截面中心的距离.得到各纤维应变后,便可根据不同材料的应力-应变本构关系确定纤维单元的应力σi,相关本构将在下文讨论.
1.1.2 截面平衡方程及迭代准则针对受弯截面,可得到两个内力平衡方程.假设弯矩荷载为M,根据各纤维单元应力便可得到相应方程.此处,将初始预应力视作偏心的轴向力荷载(Np为预应力筋初始内力、ap为预应力筋到梁底的距离).方程如下:
| $ \sum {{X_{总}}} = 0,\sum\limits_{i = 1}^n {{\sigma _i}\Delta {A_i} + {N_{\rm{p}}}} = 0. $ | (2) |
| $ \sum {{M_{总}}} = 0,M + \sum\limits_{i = 1}^n {{\sigma _i}\Delta {A_i}{Z_i} + {N_{\rm{p}}}\left( {h/2 - {a_{\rm{p}}}} \right)} = 0. $ | (3) |
当假定的ε值使得式(2)满足条件时,则式(3)中M即为确定φ值下的弯矩;若不满足式(2),则不断调整ε值,直至满足条件.本文中ε值的迭代采用二分法,ε∈(-0.003 3, 0.02),通过夹逼方式得到满足精度要求的ε值[14].
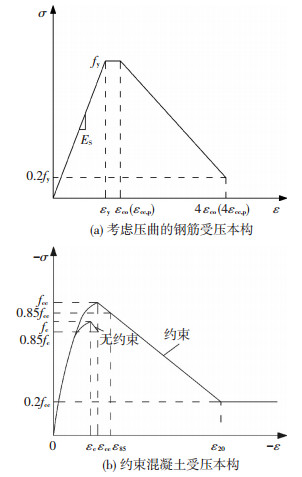
1.1.3 材料本构型钢及普通受拉钢筋采用理想弹塑性模型.预应力筋在张拉阶段视为外荷载,而在受力阶段则等效为普通钢筋处理并考虑屈服后的强度硬化,等效屈服强度fye=fpy-σp0.受压普通钢筋则采用如图 2(a)所示本构,可考虑钢筋压曲后的退化作用[15].
|
图 2 材料本构关系 Figure 2 Constitutive relationship of materials |
混凝土受拉本构采用GB 50010—2010混凝土规范的应力-应变关系[16];无约束区及约束区混凝土受压本构模型参考文献[17],该模型由Saatcioglu等[18]在其1992年提出的普通强度混凝土约束本构的基础上进行了修正,使其适用范围延伸至高强混凝土(见图 2(b)).
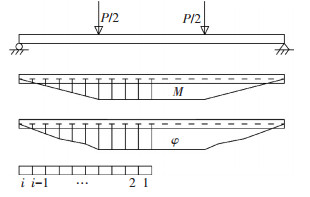
1.2 荷载-位移曲线计算图 3给出了两点加载下简支梁的弯矩和曲率分布情况.本文在求解荷载-位移曲线时采用分级加曲率法.以跨中截面曲率φmid作为加载控制值.计算步骤为:1)分级增加φmid=φmid+Δφmid;2)根据1.1节所得M-φ关系曲线,可由φmid值确定跨中弯矩Mmid,进而确定外荷载P;3)由P可得到各梁段的弯矩值Mi;4)根据Mi和M-φ关系曲线可得各梁段曲率φi,此时可利用式(4)计算跨中位移;5)检查试件是否达到破坏准则,若未破坏则重复上述步骤.
| $ {\theta _i} = \sum\limits_{j = 1}^i {{\varphi _i}{\rm{d}}x} ,i \in \left( {1,n} \right);\delta = \sum\limits_{i = 1}^n {{\theta _i}{\rm{d}}x} . $ | (4) |
|
图 3 弯矩、曲率分布 Figure 3 Distribution of bend moment and curvature |
另外,在跨中截面达到极限弯矩后,为获得荷载-位移曲线的下降段,需要进行卸载处理.塑性铰区卸载刚度按M-φ关系曲线的卸载刚度取值,其余区域按截面初始刚度卸载[14].对于两点加载的梁,塑性铰区长度lp取纯弯段长度;对于集中加载梁,lp可按0.5h0估算[19].
1.3 试验验证对文献[9]中PSRHC简支梁试件的静载试验进行模拟,验证其可靠性.试验过程中,随着普通钢筋、型钢的逐步屈服以及钢绞线应力的增大,梁试件的荷载-位移曲线不断提升.达到极限荷载时,保护层高强混凝土发生脆性破坏,荷载出现骤降现象.极限荷载后,由于型钢的存在,试件仍具有良好承载能力,荷载-位移曲线存在平稳下降段.
文中为模拟高强混凝土脆性破坏现象,在计算截面M-φ关系曲线时,假设非约束区混凝土压应力由峰值下降至其85%时,视作退出工作(即应力为0).表 1列出了开裂荷载Fcr和极限荷载Fu试验与数值结果的对比.开裂荷载计算值与试验值基本一致,而极限荷载计算值则略低于试验值.
| 表 1 数值结果与试验结果比较 Table 1 Comparison between numerical and test results |
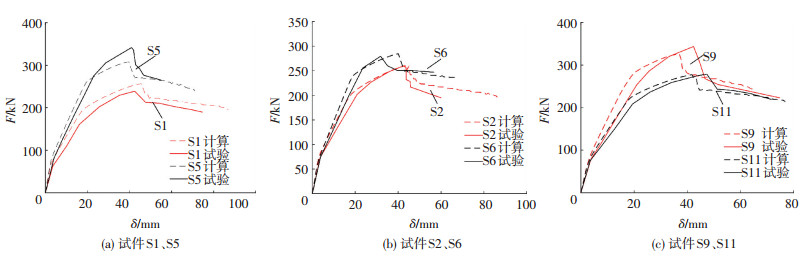
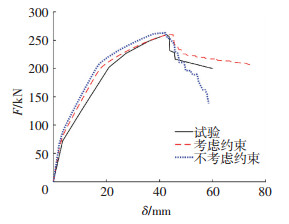
图 4为部分试件荷载-位移曲线的试验与计算结果对比.数值模型较好地模拟了荷载骤降现象及极限后曲线的平稳下降.图 5体现了核心区混凝土是否考虑约束作用的影响.若核心区混凝土采用非约束本构,则达到极限荷载后,承载力迅速下降,无荷载骤降后的平稳段,与实际不符.数值结果表明,PSRHC梁在极限后仍具有良好承载力不仅与内置型钢有关,有效的箍筋约束同样起到了积极作用.总体而言,该数值方法可较好模拟PSRHC梁的静载受力性能.
|
图 4 荷载-位移曲线数值与试验结果 Figure 4 Numerical and test load-deflection curves |
|
图 5 箍筋约束作用影响 |
以文献[9]试验梁为模型基础进行多参数分析,参数水平等级如表 2所示,共计75个试件.除混凝土强度等级、受拉及受压钢筋配筋率(ρst及ρsc)、预应力筋配筋率(ρp)、型钢翼缘及腹板厚度(tf及tw),还研究了箍筋直径(dh)及间距(sh)对延性的影响.其中,ρst=As/bh(0.51%~1.27%)、ρsc=As'/bh(0.38%~0.85%)、ρp=Ap/bh(0.23%~0.7%).As、As'、Ap分别为受拉钢筋、受压钢筋、预应力筋面积.需要注意,数值分析时钢材强度同文献[9]取值,混凝土轴心抗压强度fc则根据文献[20],按式(5)计算:
| $ {f_{\rm{c}}} = 0.669f_{{\rm{cu}}}^{1.0509}, $ | (5) |
| 表 2 数值试验影响参数及水平等级 Table 2 Design parameters and different levels |
式中fcu为立方体抗压强度.
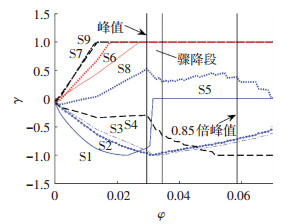
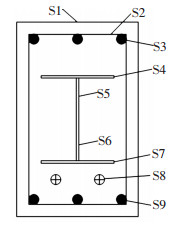
2.1 截面应力分析图 6所示为截面各位置上材料应力随截面曲率的变化情况,S1~9对应位置依次为受压非约束区顶层混凝土纤维、约束区顶层混凝土纤维、受压钢筋、上翼缘、上部腹板、下部腹板、下翼缘、预应力钢绞线、受拉钢筋(见图 7).此处γ等于实际应力与钢材屈服应力(对于混凝土则取峰值应力)之比.γ为负值,表示受压.
|
图 6 截面纤维应力发展情况 Figure 6 Development of stress in section fibers |
|
图 7 各截面纤维位置分布 Figure 7 Distibution of the section fibers |
由图 6可见:1)峰值弯矩前,随着曲率增加,S7、S9、S6率先屈服,之后S1达到峰值应力,由于混凝土强度高,有效减小了受压区高度,使得上部腹板S5处于受拉状态;2)达到峰值弯矩时,S8及S3亦屈服,而S4仅达到屈服应力的0.3左右;3)峰值后,由于S1退出工作,截面弯矩骤降,在此阶段内,上翼缘S4中应力增加速度突然变快,而上部腹板S5则向相反方向发展;4)当截面变形较大时,S4最终受压屈服,S5则由受拉向受压转变.由于内置型钢的存在及高强混凝土的脆性崩裂等多种因素,PSRHC截面中会发生复杂的应力重分布.
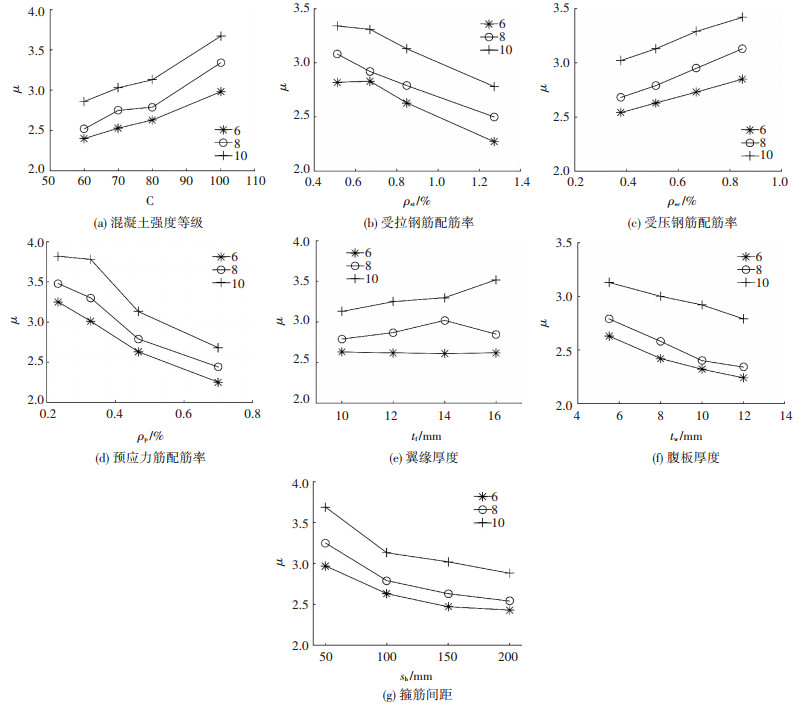
2.2 不同参数的影响分析试件或结构的延性时常用延性系数μ进行量化,该指标可反映其极限状态后的变形能力,可表示为μ=Δu/Δy.其中,Δu为极限位移,对应承载力下降至极限荷载的85%;Δy为屈服位移,采用等效能量法计算[4].图 8(a)~(g)所示为不同参数对延性系数的影响.
|
图 8 各参数对延性系数的影响 Figure 8 Parameters' effect on ductility |
1) 混凝土强度等级(图 8(a)):混凝土强度等级由C60提高至C100,对应dh为6、8、10 mm的PSRHC梁的延性系数μ分别提高了24%、32%、28%.对于非约束混凝土,强度等级越高,则混凝土的脆性越显著.但对于约束区混凝土,高等级混凝土的变形能力会得到显著提高.
2) 普通钢筋影响(图 8(b)、(c)):随着受拉钢筋增大,试件延性下降,ρst由0.51%增大至1.27%,3组试件μ值分别降低了19%、19%、17%;而增加受压钢筋用量,则可提升试件的延性,ρsc由0.37%增大至0.85%,3组试件μ值分别提高了12%、17%、13%.增大受拉钢筋使得截面受压区高度增加,从而降低试件变形能力.而增加受压钢筋的作用则刚好相反.
3) 预应力钢绞线(图 8(d)):增大预应力筋用量将明显降低PSRHC试件的延性,ρp由0.23%增大至0.70%时,3组μ值分别减小了31%、30%、30%.增大预应力筋同样会增加受压区高度,降低试件变形能力.
4) 型钢影响(图 8(e)、(f)):3组试件中,翼缘厚度tf对μ的影响规律并不明显,其变化值分别为-0.4%、2%、12%;增加腹板厚度,将降低试件的延性,tw由5.5 mm增大至12 mm时,3组试件μ值分别降低了15%、16%、11%.增加腹板的厚度变相增大了受拉钢材的用量,使得截面受压区高度增加,延性降低.
5) 箍筋的影响(图 8(g)及各平行组):增大箍筋间距,试件的延性将减小,sh由50 mm增加至200 mm,3组试件μ值分别降低了18%、22%、22%;根据平行组间μ值比较可得,当dh由6 mm增大至10 mm,延性系数增大18%~34%.箍筋用量的增加,提高了混凝土的变形能力,从而提高试件的整体延性.
为比较各参数对μ值的影响程度,可利用μ值变化程度与对应参数变化程度之比进行判别.经计算,各参数对μ值的影响程度由大到小依次为:混凝土强度等级、箍筋直径dh、箍筋间距sh、预应力筋用量ρp、受拉钢筋用量ρst、腹板厚度tw、受压钢筋用量ρsc、翼缘厚度tf.
3 公式建立根据上文分析,可将影响试件延性的参数分为两类:截面设计参数和箍筋作用.其中,截面设计参数包括混凝土强度、普通钢筋、型钢、预应力钢绞线等,可用综合配筋指标ωe进行统一考虑,先得到与ωe相关的μ的基础值μ0(ωe).另外,由上节分析可知,在ωe相同的情况下,增加箍筋用量(减小sh或增加dh)会提高μ值,故可用一个与体积配箍率相关的影响系数γh(ρsv)进行考虑.则μ为
| $ \mu = {\gamma _{\rm{h}}}{\mu _0}. $ | (6) |
本节将结合数值试验结果及回归拟合方法,详细介绍如何确定γh与ωe的值.
3.1 综合配筋指标的确定已有文献中定义的综合配筋指标对受压钢筋及型钢的作用考虑并不充分[9].而从上节分析可知,其影响不可忽视,故应对PSRHC构件中的设计参数进行全面考虑.本文综合配筋指标ωe为
| $ {\omega _{\rm{e}}} = \left( {{A_{\rm{s}}}{f_{\rm{y}}} - {{A'}_{\rm{s}}}{{f'}_{\rm{y}}} + {k_1}{\alpha _1}{A_{\rm{w}}}{f_{{\rm{sy}}}} + {k_2}{\alpha _2}{A_{{\rm{sf}}}}{f_{{\rm{sy}}}} + {k_3}{A_{\rm{p}}}{f_{\rm{p}}}} \right)/b{h_0}{f_{\rm{c}}}, $ | (7) |
式中:As、As'、Ap、Aw、Asf、h0分别为受拉、受压钢筋、预应力筋、腹板、单侧翼缘面积及受拉钢筋至梁顶距离;fy、fy'、fsy、fc、fp分别为受拉、受压钢筋屈服强度、型钢屈服强度、混凝土轴心抗压强度、预应力筋有效应力;k1、k2、k3、α1、α2分别为腹板合力、翼缘合力、预应力筋的位置等效系数及腹板、翼缘合力系数.
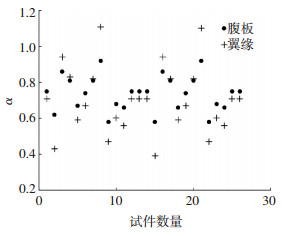
3.1.1 α1、α2、fp的确定α1=Fw/Awfsy,α2=Fsf/Asffsy.Fw、Fsf分别为极限荷载时腹板合力和上下翼缘合力.选取各变量组中设计参数为上、下限的试件进行深入分析,参考2.1节截面应力分析可得到α1、α2值(见图 9).α1在0.6~0.9浮动,集中于0.6~0.8,相对稳定.为简便起见,计算时α1取常值,等于试验样本的平均值0.75.
|
图 9 腹板、翼缘合力系数α1、α2 Figure 9 Coefficient α1 and α2 |
α2则在0.4~1.2波动,离散程度较大,若仍按样本均值取则偏差较大,但若每次均采用截面分析方法进行精确计算显然是不切实际的.可通过某一简化的指标α2'与α2间建立联系.在截面分析过程中,发现截面受压区高度在h/3附近波动,此处先假定PSRHC截面受压区高度等于h/3,则可得到假定条件下的α2'值为
| $ {{\alpha '}_2} = \frac{{{\beta _1}{f_{\rm{c}}}bh/3 - {A_{\rm{s}}}{f_{\rm{y}}} + {{A'}_{\rm{s}}}{{f'}_{\rm{y}}} - {A_{\rm{p}}}{f_{\rm{p}}} - 0.75{A_{\rm{w}}}{f_{{\rm{sy}}}}}}{{{A_{{\rm{sf}}}}{f_{{\rm{sy}}}}}}, $ | (8) |
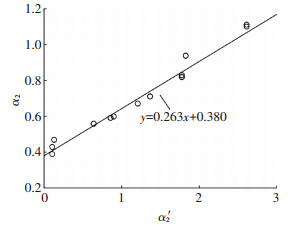
由图 10可见,α2'与α2真值间存在较好的线性关系,经数值回归可得到:
| $ {\alpha _2} = 0.263{{\alpha '}_2} + 0.38. $ | (9) |
|
图 10 α2'与α2关系 Figure 10 Relationship between α2' and α2 |
fp可由截面分析方法或混凝土规范[16]计算得到,当张拉应力较高时可直接取屈服值.
3.1.2 k1、k2、k3的确定k1、k2、k3可按下式计算:
| $ \left\{ \begin{array}{l} {k_1} = {d_{{\rm{wc}}}}/{f_0},\\ {k_2} = {d_{{\rm{sfc}}}} = {h_0},\\ {k_3} = {h_{\rm{p}}}/{h_0}. \end{array} \right. $ | (10) |
式中dwc、dsfc、hp分别为腹板合力、翼缘合力及预应力筋至梁顶距离.
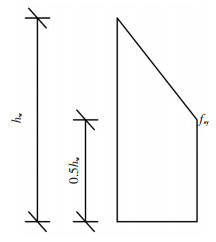
由上文得α1为0.75,为简便起见,假设腹板应力分布见图(11),则可得
| $ {d_{{\rm{wc}}}} = {h_{{\rm{wc}}}} + {h_{\rm{w}}}/9, $ | (11) |
|
图 11 假定腹板应力分布 Figure 11 Stress distribution of steel web |
式中hw、hwc分别为腹板高度及腹板中心至梁顶距离.另外,已知α2值及型钢位置后,可计算得
| $ {d_{{\rm{sfc}}}} = \left( {{h_{{\rm{sf}}}} + \left( {{\alpha _2} - 1} \right){{h'}_{{\rm{sf}}}}} \right)/{\alpha _2}, $ | (12) |
式中hsf, hsf'分别为下翼缘、上翼缘中心至梁顶距离.
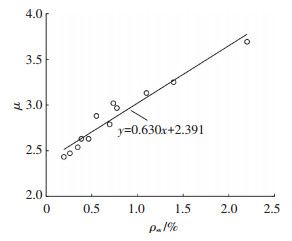
3.2 箍筋约束的影响以体积配箍率ρsv综合考虑箍筋直径及间距的影响,ρsv=AsvL/bhsh.其中,Asv和L分别为单肢箍筋面积和箍筋周长.图 12为不同体积配箍率对延性系数的影响.可见,ρsv与延性系数μ呈良好的线性关系.经数值回归可得到ρsv与μ之间的关系,见式(13).由于本文对μ0的拟合将基于ρsv=0.388%的水平组,故通过将式(13)除以ρsv=0.388%对应的μ值进行归一化处理,从而得到影响系数γh的计算公式为:
| $ \mu = 0.630{\rho _{{\rm{sv}}}} + 2.391, $ | (13) |
| $ {\gamma _{\rm{h}}} = 0.239{\rho _{{\rm{sv}}}} + 0.909, $ | (14) |
|
图 12 体积配箍率的影响 Figure 12 Effect of hoop volumetric ratio |
式中ρsv单位为%.
3.3 公式建立及标定基于ρsv=0.388%的水平组,利用二次多项式进行数值回归得到:
| $ {\mu _0} = 27.475\omega _{\rm{e}}^2 - 18.921{\omega _{\rm{e}}} + 5.353, $ | (15) |
其相关系数为0.92,将式(14)、(15)代入式(6)得到延性系数μ的计算公式为
| $ \mu = \left( {0.239{\rho _{{\rm{sv}}}} + 0.909} \right)\left( {27.475\omega _{\rm{e}}^2 - 18.921{\omega _{\rm{e}}} + 5.353} \right). $ | (16) |
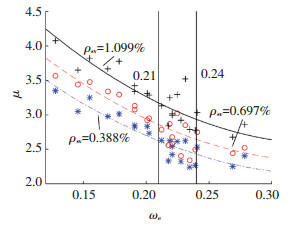
图 13所示为式(16)拟合曲线与数值试验结果比较.ωe为0.21~0.24时,数值结果存在较大波动.经分析,式(16)计算结果与数值试验结果比值的均值为0.96,标准差为0.05,总体拟合效果较好.
|
图 13 公式拟合曲线 Figure 13 Equation regression curves |
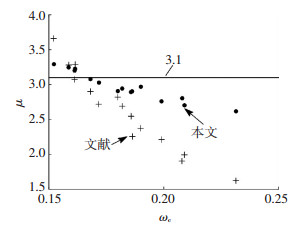
式(16)对PSRHC试件的延性进行了量化,但仍无法根据μ值预估试件的延性.有必要给出某个界限值来判别延性的优良情况.利用文献[9]试验数据,对式(16)进行界限值标定.以往对构件延性的研究表明,当延性系数为3~5时,认为构件延性良好[21].经分析可得,延性系数大于3的试验试件所对应的公式计算结果的界限值约为3.1,见图 14.
|
图 14 本文公式与试验结果 Figure 14 Regression equation and test results |
另外发现,式(16)计算结果的趋势与试验结果一致,但其变化幅度较试验结果要小得多.一方面是由于延性系数的计算方法存在差异; 其次是数值模型与实际情况间存在差异,如无法考虑钢材与混凝土间的粘结滑移等.本文公式适用于ωe属于0.12~0.28的情况;当μ值大于3.1时,认为试件延性良好.
对于给定设计参数的PSRHC梁试件,利用本文方法估计延性时,可按下列步骤计算:1)根据式(8)~(12)确定系数k1、k2、k3、α2,从而按式(7)确定ωe;2)计算体积配箍率ρsv后,根据式(16)得到μ,并与界限值进行比较.
4 结论1) 基于截面纤维模型的数值模型可考虑箍筋对混凝土的约束作用,可模拟PSRHC梁中混凝土脆性崩裂后的承载力骤降现象.利用此模型计算得到的开裂荷载、极限荷载及荷载-位移曲线与试验结果吻合良好.在配置足够箍筋的前提下,PSRHC试件同样可具备良好的延性.
2) 由参数分析结果可知,在箍筋有效约束作用的情况下,增大混凝土强度等级,可提高PSRHC梁的延性;增加受拉钢筋或预应力筋用量,增大腹板厚度,均使得延性降低;增加受压钢筋及箍筋用量,将会提高构件的延性;型钢翼缘厚度对延性的影响规律不明显.其中,箍筋间距由50 mm增加至200 mm时,延性系数降低约20.6%;箍筋直径由6 mm增大至10 mm,延性系数增大18%~34%.
3) 本文数值试验样本中,各参数对μ值的影响程度由大到小依次为:混凝土强度等级、箍筋直径dh、箍筋间距sh、预应力筋用量ρp、受拉钢筋用量ρst、腹板厚度tw、受压钢筋用量ρsc、翼缘厚度tf.
4) 基于数值试验结果,结合应力分析及回归拟合方法,建立了可考虑箍筋约束影响的延性系数计算公式.利用本文方法估计PSRHC构件延性时,μ取3.1为判断延性优劣的界限值.且本文方法适用于ωe为0.12~0.28的PSRHC试件.
| [1] |
傅传国, 李玉莹, 梁书亭. 预应力型钢混凝土简支梁受弯性能试验研[J]. 建筑结构学报, 2007, 28(3): 62-73. FU Chuanguo, LI Yuying, LIANG Shuting. Experimental study on simply supported prestressed steel reinforced concrete beams[J]. Journal of Building Structures, 2007, 28(3): 62-73. DOI:10.3321/j.issn:1000-6869.2007.03.009.issn:1000-6869.2007.03.009 |
| [2] |
王钧, 邬丹, 郑文忠. 预应力H型钢混凝土简支梁正截面受力性能试验[J]. 哈尔滨工业大学学报, 2009, 41(6): 22-27. WANG Jun, WU Dan, ZHENG Wenzhong. Experimental research on flexural mechanical behavior of simple prestressed H-steel reinforced concrete beam[J]. Journal of Harbin Institute of Technology, 2009, 41(6): 22-27. |
| [3] |
王连广, 慕光波. 预应力空腹式钢骨混凝土梁受弯性能研究[J]. 工程力学, 2011, 28(8): 113-118. WANG Lianguang, MU Guangbo. Research on bending performance of prestressed lattice type steel reinforced concrete beam[J]. Engineering Mechanics, 2011, 28(8): 113-118. |
| [4] |
金怀印, 薛伟辰, 杨晓, 等. 预应力型钢混凝土梁-钢管混凝土柱节点抗震性能试验研究[J]. 建筑结构学报, 2012, 33(8): 66-74. JIN Huaiyin, XUE Weichen, YANG Xiao, et al. Experimental research on seismic behavior of connection between prestressed steel reinforced concrete beam and concrete-filled steel tubular column[J]. Journal of Building Structures, 2012, 33(8): 66-74. DOI:10.14006/j.jzjgxb.2012.08.010.jzjgxb.2012.08.010 |
| [5] |
高峰, 熊学玉. 预应力型钢混凝土框架静力试验研究和设计理论[J]. 湖南大学学报(自然科学版), 2012, 39(8): 19-26. GAO Feng, XIONG Xueyu. Experimental Investigation and Design Theories on prestressed steel reinforced concrete frame[J]. Journal of Hunan University (Natural Science), 2012, 39(8): 19-26. |
| [6] |
高峰, 熊学玉. 预应力型钢混凝土框架结构竖向反复荷载作用下抗震性能试验研究[J]. 建筑结构学报, 2013, 34(7): 62-71. GAO Feng, XIONG Xueyu. Experimental study on seismic performance of prestressed steel reinforced concrete frame structure under vertical reversed loading[J]. Journal of Building Structures, 2013, 34(7): 62-71. DOI:10.14006/j.jzjgxb.2013.07.010 |
| [7] |
孟刚, 贾金青, 朱伟庆. 预应力型钢超高强混凝土梁抗弯性能试验研究[J]. 工程力学, 2014, 31(5): 203-210. MENG Gang, JIA Jinqing, ZHU Weiqing. Experimental study on flexural behavior of prestressed steel reinforced ultra-high strength concrete beams[J]. Engineering Mechanics, 2014, 31(5): 203-210. |
| [8] |
贾金青, 姚大立, 余芳. 预应力型钢超高强混凝土梁受剪承载力试验研究[J]. 工程力学, 2014, 31(8): 126-133. JIA Jinqing, YAO Dali, YU Fang. Experimental study on shear capacity of prestressed Ⅰ-steel ultrahigh reinforced concrete beams[J]. Engineering Mechanics, 2014, 31(8): 126-133. |
| [9] |
贾金青, 孟刚, 封硕, 等. 预应力型钢超高强混凝土梁抗弯延性试验[J]. 哈尔滨工业大学学报, 2015, 47(4): 64-70. JIA Jinqing, MENG Gang, FENG Shuo, et al. Flexural ductility of prestressed steel reinforced ultra-high strength concrete beams[J]. Journal of Harbin Institute of Technology, 2015, 47(4): 64-70. DOI:10.11918/j.issn.0367-6234.2015.04.011 |
| [10] |
蒲心诚, 王志军, 王冲, 等. 超高强高性能混凝土的力学性能研究[J]. 建筑结构学报, 2002, 23(6): 49-55. PU Xincheng, WANG Zhijun, WANG Chong, et al. Mechanical properties of super high-strength and high performance concrete[J]. Journal of Building Structures, 2002, 23(6): 49-55. |
| [11] |
R. 帕克, T. 波利. 钢筋混凝土结构(上册)[M]. 秦文钺等译. 重庆: 重庆大学出版社, 1985.
|
| [12] |
张曰果, 阎石. 高强度螺旋箍筋约束下的高强混凝土圆柱延性分析[J]. 沈阳建筑大学学报(自然科学版), 2006, 22(5): 713-717. ZHANG Yueguo, YAN Shi. Numerical analysis on ductility of circular hsc columns confined with high-strength spiral stirrups[J]. Journal of Shenyang Jianzhu University (Natural science), 2006, 22(5): 713-717. |
| [13] |
El-TAWIL S, DEIERLEIN G G. Strength and ductility of concrete encased composite columns[J]. Journal of Structural Engineering, 1999, 125(9): 1009-1019. DOI:10.1061/(ASCE)0733-9445(1999)125:9(1009) |
| [14] |
顾祥林, 孙飞飞. 混凝土结构的计算仿真[M]. 上海: 同济大学出版社, 2002.
|
| [15] |
CHEN C C, LIN N J. Analytical model for predicting axial capacity and behavior of concrete encased steel composite stub columns[J]. Journal of Constructional Steel Research, 2006, 62(5): 424-433. DOI:10.1016/j.jcsr.2005.04.021 |
| [16] |
混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2010. Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2010. |
| [17] |
RAZVI S, SAATCIOGLU M. Confinement model for high-strength concrete[J]. Journal of Structural Engineering, 1999, 125(3): 281-289. DOI:10.1061/(ASCE)0733-9445(1999)125:3(281) |
| [18] |
SAATCIOGLU M, RAZVI S. Strength and ductility of confined concrete[J]. Journal of Structural Engineering, 1992, 118(6): 1590-1607. DOI:10.1061/(ASCE)0733-9445(1992)118:6(1590) |
| [19] |
沈聚敏, 翁义军. 钢筋混凝土构件的变形和延性[J]. 建筑结构学报, 1980, 1(2): 47-58. SHEN Jumin, WEMG Yijun. The deformation and ductility of the reinforced concrete members[J]. Journal of Building Structures, 1980, 1(2): 47-58. DOI:10.14006/j.jzjgxb.1980.02.005 |
| [20] |
王勇威, 蒲心诚, 王志军. 单轴压力下56.3~164.9 MPa混凝土的应力-应变关系[J]. 建筑结构学报, 2005, 26(1): 97-102. WANG Yongwei, PU Xincheng, WANG Zhijun. Stress-strain response of concrete with different cubic compressive strength (56.3~164.9 MPa) under uniaxial compression[J]. Journal of Building Structures, 2005, 26(1): 97-102. DOI:10.14006/j.jzjgxb.2005.01.015 |
| [21] |
江见鲸, 李杰, 金伟良. 高等混凝土结构理论[M]. 北京: 中国建筑工业出版社, 2006.
|
 2018, Vol. 50
2018, Vol. 50



 14
14