引用本文

崔济东, 韩小雷, 季静, 龚涣钧. RC梁的变形性能指标限值研究与试验验证[J]. 哈尔滨工业大学学报, 2018, 50(6): 169-176. DOI: 10.11918/j.issn.0367-6234.201706082.

CUI Jidong, HAN Xiaolei, JI Jing, GONG Huanjun. Experimental study on deformation limits of RC beams[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 169-176. DOI: 10.11918/j.issn.0367-6234.201706082.

基金项目

国家自然科学基金(51378221);亚热带建筑科学国家重点实验室基金(2015ZA05)

作者简介

崔济东(1988—), 男, 博士;
韩小雷(1964—), 男, 教授, 博士生导师

通信作者

韩小雷, xlhan@scut.edu.cn

文章历史

收稿日期: 2017-06-12

Abstract Full text Figures/Tables PDF

RC梁的变形性能指标限值研究与试验验证

崔济东¹, 韩小雷^1,2, 季静¹, 龚涣钧¹

1. 华南理工大学土木与交通学院，广州 510641;
2. 亚热带建筑科学国家重点实验室(华南理工大学)，广州 510641

收稿日期: 2017-06-12

基金项目: 国家自然科学基金(51378221);亚热带建筑科学国家重点实验室基金(2015ZA05)

作者简介: 崔济东(1988—), 男, 博士;
韩小雷(1964—), 男, 教授, 博士生导师

通信作者: 韩小雷, xlhan@scut.edu.cn

摘要: 为建立钢筋混凝土(RC)梁的变形性能指标限值，对RC梁的分类方法、性能状态划分方法及各性能状态变形限值的确定方法进行了研究.对于RC梁的分类方法，基于收集的103个RC梁的低周往复荷载试验结果对RC梁破坏形态的影响因素进行研究，将RC梁划分为弯控及剪控两类，并以剪跨比和弯剪比为参数给出两类构件的划分准则.对于RC梁的性能状态及其变形限值，根据中国现行规范将RC梁的抗震性能状态划分为7个等级，基于构件的力-位移角骨架曲线的3个关键性能点(屈服点、承载力退化20%点及丧失承载能力点)提出了RC梁各性能状态变形限值的确定方法.在此基础上，对103个RC梁试验结果进行多组不同参数的回归分析，获得弯控及剪控RC梁3个关键性能点变形限值的控制参数及回归公式，依此建立了弯控及剪控RC梁的变形指标限值.为进一步验证提出的RC梁变形指标限值合理性，进行了9个RC梁的拟静力试验，将试验位移角限值与提出的变形限值进行了对比，结果表明，本文提出的RC梁变形性能指标限值的准确性、离散性及超越概率均在合理范围内.

关键词: 变形限值破坏形态钢筋混凝土梁拟静力试验易损性评估

Experimental study on deformation limits of RC beams

CUI Jidong¹, HAN Xiaolei^1,2, JI Jing¹, GONG Huanjun¹

1. School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510641, China;
2. State Key Laboratory of Subtropical Building Science (South China University of Technology), Guangzhou 510641, China

Abstract: To establish deformation limits of reinforced concrete(RC) beams, study on the method for classification of RC beams, definition of performance states and determining the deformation limit of specific performance state was conducted. As for the classification of RC beams, parameters affecting the failure modes of RC beams were investigated using collected test data for 103 RC beams tested under low frequency cyclic loading. A method was proposed to classify the failure modes into flexure-controlled and shear-controlled based on shear span ratio and moment shear ratio of beams. As for the performance states of RC beams and their deformation limits, the performance states of RC beams were divided into seven levels with reference to the current Chinese codes for seismic design, and the method for determining the deformation limits of these levels was put forward, which is based on three key performance points (point of yielding, point of losing 20% load capacity, point of losing bearing capacity) of the force-drift ratio backbone curves. With the test data of 103 RC beams, regression analysis of deformation limits was performed on multiple sets of parameters, key parameters and formula of deformation limits of the three key performance points were found for the flexure-controlled and shear-controlled RC beams. Deformation limits of flexure-controlled and shear-controlled RC beams were then put forward. To further verify the proposed deformation limits, quasi-static test of 9 RC beams was conducted, test deformation limits of three key performance points were obtained and compared to the proposed performance limits. The results show that the accuracy, discreteness and failure probability of the proposed RC beam deformation limits are all within reasonable range.

Key words: deformation limits failure modes reinforced concrete beam quasi-static test fragility evaluation

梁作为重要的受力构件，其变形性能对建筑结构的整体抗震性能有重要的影响.中国GB 50011—2010《建筑抗震设计规范》^[1]引入了基于性能的抗震设计思想，但在构件抗震性能评估上依然采用以承载能力验算为主的评估方法，构件在罕遇地震作用下的变形需求主要由相关的构造措施来保证，尚未给出构件的变形性能指标限值，无法进行构件层次损伤的定量评估.虽然国内外很多文献[2-8]对钢筋混凝土(RC)梁的变形性能指标限值进行了研究，但这些研究成果主要集中在弯控RC梁上，对RC梁的破坏形态划分方法及非弯控RC梁的变形性能指标限值研究比较少，这些问题均不利于建立系统的RC梁变形性能指标限值体系.

本文基于收集的103个矩形RC梁试验数据，对RC梁的破坏形态影响因素进行分析，提出RC梁的破坏形态划分方法.根据中国现行规范，对RC梁的性能状态进行划分，并基于构件力-位移角骨架曲线的3个关键性能点(屈服点、承载力下降20%点及丧失承载能力点)提出RC梁各性能状态变形指标限值的统一确定方法.在此基础上，结合103个RC梁试验结果的回归分析，建立RC梁的变形性能指标限值，并对其进行易损性评估，检验指标限值的准确性、离散性和超越概率.最后进行9个RC梁的低周往复荷载试验，利用试验结果进一步对提出的指标限值进行验证.

1 RC梁试验数据整理

为进行RC梁的变形性能指标限值研究，从公开发表的文献收集了103个RC梁试件低周往复荷载试验数据，提取了各试件的关键参数并汇编成数据库.数据库中所有试件试验过程中位移均为逐级增大直至试验停止，以下给出该数据库的数据来源及主要参数分布，如表 1所示.表中，f_ck为混凝土的试验轴心抗压强度标准值，λ为剪跨比，ρ_t为梁加载方向的面积配箍率，λ_v为梁的配箍特征值，V/f_ckbh₀为名义剪压比，m为弯剪比.其中，剪跨比λ、配箍率ρ_t按GB 50010—2010《混凝土结构设计规范》^[9](简称"2010《混规》")的定义计算，弯剪比m、名义剪压比V/f_ckbh₀、配箍特征值λ_v分别按式(1)~(3)计算：

$ m = {M_{\rm{n}}}/\left( {{V_{\rm{n}}}{L_{\rm{a}}}} \right), $

(1)

$ V/\left( {{f_{{\rm{ck}}}}b{h_0}} \right) = \min \left( {{M_{\rm{n}}}/{L_{\rm{a}}},{V_{\rm{n}}}} \right)/\left( {{f_{{\rm{ck}}}}b{h_0}} \right), $

(2)

$ {\lambda _{\rm{v}}} = {\rho _{\rm{v}}}{f_{\rm{y}}}/{f_{{\rm{ck}}}}. $

(3)

表 1 RC梁的主要试验参数 Table 1 Main experimental data of RC beams

数量	文献	f_ck/MPa	λ	ρ_t/%	λ_v	m	V/f_ckbh₀
3	[10]	22.53~29.36	3.09	0.34~0.87	0.06~0.14	0.41~0.99	0.065~0.095
8	[11]	24.46~29.60	2.75~4.45	0.31~0.62	0.06~0.12	0.20~0.60	0.025~0.085
2	[12]	33.86~35.81	3.28	0.28~0.51	0.05~0.09	0.24~0.34	0.023~0.025
7	[13]	24.96~25.51	2.52~3.53	0.64~1.61	0.08~0.21	0.58~1.43	0.110~0.186
10	[14]	15.18	2.08	0.20	0.04	1.34~2.67	0.091
8	[15]	19.69~29.04	2.00	0.14~0.15	0.02~0.04	1.15~2.39	0.069~0.088
1	[16]	35.03	1.76	0.61	0.13	0.35	0.047
4	[17]	32.09~50.44	3.21	0.61~0.69	0.07~0.13	0.58~0.72	0.053~0.084
9	[18]	14.33~15.69	3.85	0.50	0.11~0.12	0.06~1.03	0.008~0.144
6	[19]	49.90	1.67~2.22	0.7~1.4	0.09~0.17	0.49~0.65	0.051~0.112
2	[20]	15.65~23.02	5.19	0.47	0.05~0.08	0.59~0.74	0.049~0.08
8	[21]	45.64~46.69	3.00	0.43~0.52	0.04~0.06	0.24~0.48	0.019~0.035
2	[22]	28.50	2.64~3.85	0.31	0.04	0.18~0.25	0.013~0.019
8	[23]	19.93~31.81	0.52~1.97	0.39~1.23	0.05~0.24	0.70~1.24	0.087~0.172
2	[24]	27.79~27.91	0.52~0.90	1.03	0.13~0.14	0.65~0.68	0.112~0.116
2	[25]	21.07~22.2	0.37~0.52	1.15~1.51	0.21~0.29	0.47~0.81	0.156~0.207
11	[26]	24.02	2.78~3.85	0.22~0.90	0.03~0.20	0.18~0.84	0.026~0.097

表 1 RC梁的主要试验参数 Table 1 Main experimental data of RC beams

式中：M_n和V_n分别为按2010《混规》6.2节及6.3.12节计算的加载方向的抗弯和抗剪承载能力，计算时钢筋的强度取试验屈服强度平均值，混凝土强度取标准值；L_a为试件的剪跨，对于悬臂构件，等于构件的悬臂长度；V为M_n/L_a和V_n中的较小值；b为垂直加载方向梁的截面宽度，h₀为梁加载方向的有效截面高度；f_y为箍筋的实测屈服强度平均值；ρ_v为梁的体积配箍率.

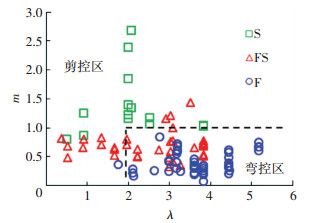
2 RC梁破坏形态划分

RC梁的破坏形态通常可分为弯曲破坏、弯剪破坏和剪切破坏^[27]，RC梁的破坏形态不同，其变形能力的影响参数也不一样，为此，在进行RC梁的变形指标限值研究前，先对RC梁的破坏形态划分方法进行研究.分析收集的103个RC梁试件的破坏形态和剪跨比λ、弯剪比m、名义剪压比V/(f_ckbh₀)、配箍特征值λ_v、加载方向箍筋配箍率ρ_t的关系，最终确定，能够较好区分RC梁破坏形态的主要参数有剪跨比λ和弯剪比m.总体上，剪跨比越大，构件越容易发生弯曲破坏，弯剪比越大，构件越容易发生剪切破坏.以剪跨比和弯剪比为参数，提出RC梁的破坏形态划分准则，见表 2.表 2的划分准则与收集的103个RC梁试件破坏形态的关系如图 1所示，详细统计结果见表 3.

表 2 RC梁的破坏形态划分准则 Table 2 Failure mode classification of RC beams

图 1 破坏形态与剪跨比、弯剪比的关系(F为弯曲破坏, FS为弯剪破坏, S为剪切破坏) Figure 1 Failure modes influenced by shear span ratio and moment shear ratio (F: flexure failure; FS: flexure-shear failure; S: shear failure)

表 3 RC梁的破坏形态划分结果 Table 3 Failure mode classification results of RC beams

如表 3所示，试验发生弯曲破坏的试件97.30%被划分为弯控，试验发生剪切破坏的试件100.00%被划分为剪控，试验发生弯剪破坏的试件62.50%被划分为弯控，37.50%被划分为剪控.由此可见，表 2的RC梁破坏形态划分方法合理，对弯曲破坏及剪切破坏这两种破坏机制截然不同的破坏形态的判别具有较高的准确率.

3 RC梁抗震性能状态划分

中国JGJ 3—2010《高层建筑混凝土结构技术规程》^[28](简称"2010《高规》")将构件的损坏状态划分为5个等级：无损坏、轻微损坏、轻度损坏、中度损坏、较严重损坏.其中具有较为明确物理意义的是"无损坏"及"较严重损坏"状态.对于"无损坏"状态，可认为在该状态下，构件基本保持弹性，该状态的极限为构件屈服；对于"较严重损坏"状态，2010《高规》附录指出，结构在罕遇地震作用下，满足第5性能水准时，有较严重的损坏，但不至于倒塌或发生危及生命的严重损坏.由于构件的倒塌严重危及生命财产安全，因此，可认为"较严重损坏"状态的极限为承载力退化20%，在该状态下，构件未倒塌，仍能承载，未完全失去抗侧力；为方便结构的抗倒塌能力评估，与文献[29]的思路类似，在第5个构件损坏状态后增加"严重损坏"和"倒塌"两个状态，其中，构件"严重损坏"状态的极限是构件丧失承载能力，发生倒塌.

课题组前期研究^[30]发现，塑性位移角能较好地反映构件的破坏程度，为此，本文以塑性位移角为变形指标，将RC梁的抗震性能状态划分为"无损坏"、"轻微损坏"、"轻度损坏"、"中度损坏"、"较严重损坏"、"严重损坏"及"倒塌"7个等级，并基于构件的力-位移角骨架曲线确定各性能状态的变形限值，如图 2所示.其中，前6个性能状态的极限对应6个性能点，"无损坏"、"较严重损坏"及"严重损坏"是构件的3个关键性能状态.图 2中，横坐标为悬臂构件的位移角，纵坐标为构件的侧向力，V_max为峰值承载力，θ₁、θ₂、θ₃、θ₄、θ₅和θ₆分别表示"无损坏"、"轻微损坏"、"轻度损坏"、"中度损坏"、"较严重损坏"、"严重损坏"状态的总位移角限值."无损坏"状态的位移角限值定义为名义屈服位移角^[31-32].如图 2所示，经过原点及0.7V_max点的割线与过峰值承载力V_max的水平直线相交于一点，从交点处做一竖直线，该竖直线与构件的力-位移角骨架曲线的交点即名义屈服点，名义屈服点的位移角θ₁即为性能1的位移角限值.在该状态下，构件处于基本弹性，受拉纵筋未屈服，产生细微裂缝，裂缝宽度一般不大于0.5 mm^[27]."较严重损坏"状态的位移角限值θ_5p取为承载力下降20%点的塑性位移角，在该状态下，部分构件纵筋压屈或拉断，箍筋脱钩失效，混凝土保护层压碎严重^[27]."严重损坏"状态的位移角限值θ_6p取侧向承载能力下降50%点对应的塑性位移角."轻微损坏"、"轻度损坏"和"中度损坏"的塑性位移角限值分别取为"较严重损坏"塑性位移角限值的0.25、0.50和0.75倍，相应的破坏现象可参考课题组前期试验研究^[27].

图 2 RC梁的性能状态及位移角限值 Figure 2 Performance states and drift ratio limits of RC beams

将本文RC梁性能状态的划分标准总结如表 4所示.由表 4可知，只需根据梁的顶点力-位移角骨架曲线获得"无损坏"、"较严重损坏"及"严重损坏"3个关键性能状态的总位移角θ₁、θ₅和θ₆，便可根据表 4的方法获得6个性能状态的位移角限值.

表 4 RC梁各性能状态的破坏现象及位移角限值 Table 4 Failure phenomena and drift ratio limits of performance states of RC beams

4 RC梁的位移角限值

为建立系统的RC梁变形性能指标限值体系，本文采用以下具体步骤：(1)选定各性能点位移角限值的目标超越概率；(2)采用多组不同的参数对弯控及剪控RC梁"无损坏"、"较严重损坏"及"严重损坏"3个关键性能状态的位移角限值进行回归分析，选取位移角限值的控制参数及回归公式；(3)采用易损性分析方法，评估第(2)步选定的回归公式的超越概率，并对回归公式进行调整，获得具有目标超越概率的回归公式，以调整后的公式初步建立RC梁各性能状态的位移角限值；(4)采用易损性分析方法，对第(3)步确定的位移角限值进行评估，若位移角限值的超越概率不大于第(1)步设定的目标超越概率，则位移角限值满足要求，否则对位移角限值再次进行调整，直到满足要求.

4.1 位移角限值超越概率的选取

美国性能评估规范ASCE/SEI 41-13^[33]给出的弯控RC梁、柱的变形指标体系中，塑性变形参数a的目标超越概率不大于35%，塑性变形参数b的目标超越概率不大于15%.由于塑性变形参数a与本文性能点5塑性变形的概念相似，塑性变形参数b与本文性能点6塑性变形的概念相似，为此，本文位移角限值的超越概率统一按以下原则选取：(1)对于性能1("无损坏"状态)的位移角限值，超越概率不大于35%，即保证率不小于65%；(2)对于性能5("较严重损坏"状态)的位移角限值，超越概率不大于35%，即保证率不小于65%；(3)对于性能6("严重损坏"状态)的位移角限值，超越概率不大于15%，即保证率不小于85%；(4)性能2、性能3及性能4的塑性位移角限值按本文第3节的原则由性能5的塑性位移角限值四等分得到.

4.2 关键性能点位移角限值的回归分析

根据表 4获得收集的103个RC梁试件"无损坏"、"较严重损坏"及"严重损坏"3个关键性能状态的位移角限值θ₁、θ_5p和θ_6p.将103个梁试验数据按表 2的划分准则分为弯控组及剪控组，以弯剪比m、名义剪压比V/(f_ckbh₀)、配箍特征值λ_v、配箍率ρ_t这4个参数的不同组合，分别建立弯控组及剪控组RC梁试件θ₁、θ_5p和θ_6p的回归公式，并从中选取相关性最强的回归公式，用于初步建立RC梁的位移角限值.对于弯控RC梁，以m、V/(f_ckbh₀)和λ_v为控制参数，对于剪控RC梁，以n和ρ_t为控制参数，最终弯控及剪控RC梁3个关键性能状态位移角限值的回归公式选取如式(4)~(9)所示.

1) 弯控RC梁的位移角限值回归公式

$ {\theta _1} = - 0.013 + 0.146{\lambda _{\rm{v}}} + 0.047m - 0.295V/\left( {{f_{{\rm{ck}}}}b{h_0}} \right), $

(4)

$ {\theta _{{\rm{5p}}}} = 0.010 + 0.264{\lambda _{\rm{v}}} + 0.058m - 0.482V/\left( {{f_{{\rm{ck}}}}b{h_0}} \right), $

(5)

$ \begin{array}{l} {\theta _{{\rm{6p}}}} = 0.0203 + 0.2107{\lambda _{\rm{v}}} + 0.0395m - \\ \;\;\;\;\;\;\;\;0.3434V/\left( {{f_{{\rm{ck}}}}b{h_0}} \right). \end{array} $

(6)

2) 剪控RC梁的位移角限值回归公式

$ {\theta _{\rm{1}}} = 0.005, $

(7)

$ {\theta _{{\rm{5p}}}} = 0.029 - 0.0077m + 0.5953{\rho _{\rm{t}}}, $

(8)

$ {\theta _{{\rm{6p}}}} = 0.037 - 0.0102m + 0.5182{\rho _{\rm{t}}}. $

(9)

4.3 回归公式的超越概率

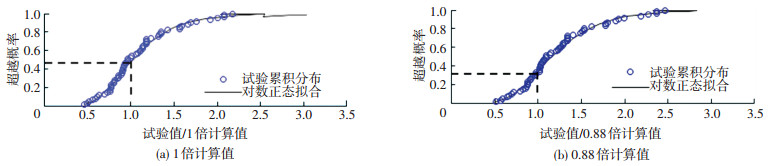
采用ATC-58^[34]建议的易损性分析方法，评估回归公式的超越概率，获得具有目标超越概率的回归公式.具体思路是，根据表 4，确定收集的103个RC梁试件"无损坏"、"较严重损坏"及"严重损坏"性能状态的试验位移角限值(试验值)，并与按4.2节选取的各组位移角限值回归公式计算的变形限值(计算值)作比，建立位移角限值的试验值与计算值比值的累积概率分布曲线，通过累积概率分布和拟合的对数正态分布曲线，可获得回归公式的超越概率.若超越概率与目标超越概率相差较大，则对回归公式进行调整，对调整后的公式进行同样的评估，获得具有目标超越概率的回归公式.图 3为弯控RC梁"无损坏"状态位移角限值回归公式的易损性曲线，由图可见，按式(4)计算的θ₁的超越概率为47.41%(图 3(a))，调整为0.88倍后超越概率接近目标超越概率35%(图 3(b)).按同样的方法，可获得其余各组回归公式的超越概率及调整后具有目标超越概率的回归公式，见表 5.

图 3 θ₁易损性曲线 Figure 3 Fragility curve of θ₁

表 5 关键性能状态下回归公式的超越概率 Table 5 Failure probability of regression formula of key performance states

4.4 位移角限值的建立

利用表 5给出的调整后具有目标超越概率的回归公式建立RC梁的位移角限值，并进行反复调整，得到最终RC梁的位移角限值，如表 6和表 7所示.表中"无损坏"性能状态的位移角限值为总位移角，其余性能状态的位移角限值为塑性位移角.当参数落在表中参数之间时，通过插值获得相应的变形限值.

表 6 RC弯控RC梁位移角限值 Table 6 Drift ratio limits of flexure-controlled RC beams

表 7 剪控RC梁位移角限值 Table 7 Drift ratio limits of shear-controlled RC beams

4.5 位移角限值的易损性评估

为验证表 6和表 7的合理性，进行指标限值的分组易损性评估，将收集的103个RC梁试验数据按表 2的破坏形态，考虑表 6和表 7中控制参数(配箍特征值λ_v、名义剪压比V/f_ckbh₀、加载方向配箍率ρ_t和弯剪比m)的主要划分区间，划分为多个小组，见表 8.

表 8 RC梁试件分组 Table 8 Bins of RC beams

由于本文RC梁"轻微损坏"、"轻度损坏"和"中度损坏"的位移角限值通过均分法得到，所以本文只对"无损坏"、"较严重损坏"和"严重损坏"3个关键性能状态的位移角限值进行评估.将收集的103个RC梁试件3个关键性能状态("无损坏"、"较严重损坏"及"严重损坏")的试验位移角限值与按表 6和表 7计算的位移角限值相比，比值记作"位移角限值冗余度".其中，位移角限值的准确性通过冗余度的平均值评估，冗余度的均值越接近1，指标限值越准确；位移角限值的离散性通过冗余度的标准差评估；位移角限值的超越概率通过易损性分析方法，建立冗余度的累积分布曲线及拟合的对数正太分布曲线进行评估.表 8各组数据位移角限值的评估结果如表 9所示.需要注意的是，由于部分分组的试件数量比较小，评估的超越概率可能不够合理，这里为了统一，均一并给出.

表 9 RC梁关键性能点位移角限值评估结果 Table 9 Evaluation results of drift ratio limits of key performance points

分组信息			超越概率/%			冗余度平均值			冗余度标准差
大组	小组	试件数量	性能1	性能5	性能6	性能1	性能5	性能6	性能1	性能5	性能6
弯控组	1	61	11	6	12	1.88	1.53	1.47	0.86	0.37	0.12
	2	15	17	13	15	1.84	1.47	1.42	0.85	0.37	0.38
	3	2	0	0	0	2.16	1.52	1.34	0.12	0.03	0.02
	4	0	—	—	—	—	—	—	—	—	—
	5	16	10	1	9	1.75	1.52	1.40	0.71	0.28	0.35
	6	15	16	6	14	1.35	1.49	1.42	0.36	0.43	0.47
	7	0	—	—	—	—	—	—	—	—	—
	8	9	1	9	16	2.64	1.68	1.52	0.82	0.50	0.48
	9	4	3	6	16	2.89	1.58	1.35	1.40	0.44	0.37
剪控组	1	42	10	13	9	2.34	1.75	1.77	1.28	0.68	0.62
	2	23	11	13	9	2.53	1.80	1.93	1.54	0.68	0.69
	3	0	—	—	—	—	—	—	—	—	—
	4	10	18	21	11	1.80	1.45	1.45	0.79	0.55	0.44
	5	9	0	5	6	2.45	1.98	1.73	0.78	0.73	0.53

表 9 RC梁关键性能点位移角限值评估结果 Table 9 Evaluation results of drift ratio limits of key performance points

由表 9可见：

1) 弯控组及剪控组性能1位移角限值的超越概率不高于35%，且均低于20%，满足目标超越概率要求；弯控组及剪控组性能5的塑性位移角限值在全局参数范围内的超越概率分别为6%和13%，小于35%，各小组的超越概率均不高于25%外，满足目标超越概率要求；弯控组及剪控组性能6的塑性位移角限值在全局参数范围内的超越概率分别为12%和9%，除个别小组的超越概率略大于15%外，大部分小组的超越概率均低于15%，总体上满足目标超越概率要求.

2) 弯控组和剪控组性能1的位移角限值冗余度平均值总体在分别在1.8和2.3左右，说明本文给出的RC梁的屈服位移角限值偏安全.弯控组和剪控组性能点5和6位移角限值冗余度平均值总体分别在1.5和1.7左右，即位移角限值的计算值与试验值的比值分别在0.67和0.59左右(1/1.5=0.67；1/1.7=0.59)，说明本文给出的RC梁的塑性位移角限值比较接近试验值，准确性较高.

3) 弯控组和剪控组性能5和6位移角限值的冗余度标准差在0.6左右，较小，表明本文给出的RC梁的塑性位移角限值离散性较小；弯控组和剪控组性能1位移角限值的冗余度标准差总体分别在0.8和1.2左右，相对较大，但考虑到RC梁性能1位移角限值的超越概率均不高于目标超越概率，因此，总体上认为本文提出的RC梁位移角限值的离散性在可接受范围内.

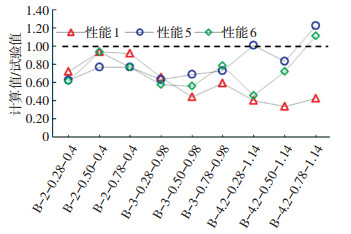
4.6 位移角限值试验验证

为进一步验证本文提出的RC梁位移角限值的合理性，考虑表 6和表 7的主要参数，按不同的剪跨比、配箍率和纵筋配筋率设计了9个对称配筋的矩形截面RC梁试件，并对其进行低周往复加载试验研究，试件的详细参数详见文献[27, 35].按表 6和表 7计算9个RC梁3个关键性能状态(性能1、性能5及性能6)的位移限值(计算值)并与根据试验结果按表 4获得的位移角限值(试验值)进行对比，结果如图 4所示，详细统计结果如表 10所示.图 4中，横坐标为试件编号，试件编号包含试件剪跨比、配箍率及单边纵筋配筋率信息，如B-2-0.28-0.4表示剪跨比为2，配箍率为0.28%，纵筋配筋率为0.4%.表 10中下标"test"表示位移角限值的试验值，下标"table"表示位移角限值的计算值.

图 4 RC梁关键性能点位移角限值计算值与试验值的比值 Figure 4 Ratio of calculated value to test value of RC beams drift ratio limits at key performance points

表 10 位移角计算值与试验值比值的统计参数 Table 10 Statistical parameters of ratio of calculated drift ratio limits to test drift ratio limits

由图 4和表 10可见，θ_1-table/θ_1-test、θ_5-table/θ_5-test及θ_6-table/θ_6-test的平均值分别为0.61、0.81和0.73，接近于1且小于1，标准差较小，分别为0.22、0.19及0.20，表明，本文给出的RC梁的位移角限值合理，较接近于试验值、离散性较小且偏于安全.

5 结论

1) 提出以剪跨比和弯剪比为参数的RC梁破坏形态划分方法，该方法判别弯曲破坏及剪切破坏的准确率分别为97.30%和100.00%.

2) 将RC梁的抗震性能划分为"无损坏"、"轻微损坏"、"轻度损坏"、"中度损坏"、"较严重损坏"、"严重损坏"及"倒塌"7个状态，并基于构件的力-位移角骨架曲线的3个关键性能点(屈服点、承载力退化20%点及丧失承载能力点)，提出RC梁各性能状态位移角限值的统一确定方法.

3) 以弯剪比、名义剪压比及约束区配箍特征值为控制参数，给出弯控RC梁的位移角限值，以弯剪比及加载方向配箍率为控制参数，给出剪控RC梁的位移角限值，并采用ATC 58建议的易损性分析方法，对给出的位移角限值进行评估，结果显示，"无损坏"、"较严重损坏"及"严重损坏"3个关键性能状态位移角限值的超越概率总体上分别不大于20%、25%及15%，且位移角限值的准确性和离散性均在合理范围内.

4) 通过作者开展的9个RC梁的拟静力试验结果，对本文提出的RC梁位移角限值进行验证，结果显示，本文给出的最重要的"较严重损坏"状态的RC梁位移角限值与试验位移角限值的比值平均为0.81，准确性较高且离散性较小.

参考文献

[1]	建筑抗震设计规范: GB 50011—2010 [S]. 北京: 中国建筑工业出版社, 2010. Code for seismic design of buildings: GB 50011—2010 [S]. Beijing: China Architecture & Building Press, 2010.
[2]	蒋欢军, 王斌, 吕西林. 钢筋混凝土梁和柱性能界限状态及其变形限值[J]. 建筑结构, 2010, 40(1): 10-14. JIANG Huanjun, WANG Bin, LV Xilin. Performance limit states and deformation limits of RC beams and columns[J]. Building Structure, 2010, 40(1): 10-14.
[3]	PANAGIOTAKOS T B, FARDIS M N. Deformations of reinforced concrete members at yielding and ultimate[J]. ACI Structural Journal, 2001, 98(2): 135-148.
[4]	BISKINIS D, FARDIS M N. Deformations at flexural yielding of members with continuous or lap-spliced bars[J]. Structural concrete, 2010, 11(3): 127-138. DOI:10.1680/stco.2010.11.3.127
[5]	BISKINIS D, FARDIS M N. Flexure-controlled ultimate deformations of members with continuous or lap-spliced bars[J]. Structural Concrete, 2010, 11(2): 93-108. DOI:10.1680/stco.2010.11.2.93
[6]	周定松, 吕西林, 蒋欢军. 钢筋混凝土框架梁的变形能力及基于性能的抗震设计方法[J]. 地震工程与工程振动, 2005, 25(4): 60-66. ZHOU Dingsong, LV Xilin, JIANG Huanjun. Deformation capacity and performance-based seismic design method for RC frame beams[J]. Earthquake Engineering and Engineering Vibration, 2005, 25(4): 60-66. DOI:10.3969/j.issn.1000-1301.2005.04.010
[7]	蒋欢军, 白努特, 陈林之. 钢筋混凝土梁柱构件的地震损伤性能试验[J]. 结构工程师, 2011, 27(2): 102-107. JIANG Huanjun, DOUMIA B, CHEN Linzhi. Experiment on seismic damage behavior of reinforced concrete beams and columns[J]. Structural Engineers, 2011, 27(2): 102-107. DOI:10.3969/j.issn.1005-0159.2011.02.018
[8]	钱稼茹, 徐福江. 钢筋混凝土梁基于位移的变形能力设计方法[J]. 四川建筑科学研究, 2007, 33(2): 1-3. QIAN Jiaru, XU Fujiang. Displacement-based deformation capacity design method of reinforced concrete beams[J]. Sichuan Building Science, 2007, 33(2): 1-3. DOI:10.3969/j.issn.1008-1933.2007.02.001
[9]	混凝土结构设计规范: GB 50010—2010 [S]. 北京: 中国建筑工业出版社, 2010. Code for design of concrete structures: GB 50010—2010 [S]. Beijing: China Architecture & Building Press, 2010.
[10]	POPOV E P, BERTERO V V, KRAWINKLER H. Cyclic behavior of three R/C flexural members with high shear: EERC Report No. 72-5[R]. Berkeley, California: Earthquake Engineering Research Center, 1972.
[11]	BERTERO V V, POPOV E P. Hysteretic behavior of ductile moment-resisting reinforced concrete frame components: EERC Report No. 75-16 [R]. Berkeley, California: Earthquake Engineering Research Center, 1975.
[12]	PANAGIOTOU M, VISNJIC T, ANTONELLIS G, et al. Effect of hoop reinforcement spacing on the cyclic response of large reinforced concrete special moment frame beams: PEER Report No. 2013-16[R]. Berkeley, California: Pacific Earthquake Engineering Research Center, 2013.
[13]	刘志强, 吴波, 林少书. 钢筋混凝土连梁的抗震性能研究[J]. 地震工程与工程振动, 2003, 23(5): 117-124. LIU Zhiqiang, WU Bo, LIN Shaoshu. Study on seismic performance of reinforced concrete coupling beams[J]. Earthquake engineering and engineering vibration, 2003, 23(5): 117-124. DOI:10.13197/j.eeev.2003.05.019
[14]	冷巧娟, 钱江, 张熠, 等. 既有钢筋混凝土梁抗震性能试验研究[J]. 建筑结构, 2011, 41(8): 26-28. LENG Qiaojuan, QIAN Jiang, ZHANG Yi, et al. Experimental study on seismic performance of existing reinforced concrete beams[J]. Building Structure, 2011, 41(8): 26-28.
[15]	杜修力, 袁健, 周宏宇, 等. 钢筋混凝土梁在低周反复荷载作用下受剪性能的尺寸效应试验研究[J]. 地震工程与工程振动, 2011, 31(5): 30-38. DU Xiuli, YUAN Jian, ZHOU Hongyu, et al. The experimental study of size effect on shear capacity of reinforced concrete beam under low cyclic loading[J]. Journal of earthquake engineering and engineering vibration, 2011, 31(5): 30-38. DOI:10.13197/j.eeev.2011.05.014
[16]	NAISH D A B. Testing and modeling of reinforced concrete coupling beams[D]. Los Angeles: University of California, Los Angeles, 2010.
[17]	XIAO Y, RUI M. Seismic behavior of high strength concrete beams[J]. Structural Design of Tall Buildings, 1998, 7(1): 73-90. DOI:10.1002/(SICI)1099-1794(199803)7:1<>1.0.CO;2-2
[18]	朱志达, 沈参璜. 在低周反复循环荷载作用下钢筋混凝土框架梁端抗震性能的试验研究(1)[J]. 北京工业大学学报, 1985, 11(1): 17-38. ZHU Zhida, SHEN Canhuang. An experimental investigation on earthquake-resistant behavior of the beam end of reinforced concrete framed buildings under low repeated and reversed loading(1)[J]. Journal of Beijing University of Technology, 1985, 11(1): 17-38.
[19]	XIAO Y, ESMAEILY G A, WU H. High-strength concrete short beams subjected to cyclic shear[J]. ACI Structural Journal, 1999, 96(3): 392-400.
[20]	周卫明. 不同屈服点钢筋混凝土结构耗能铰的试验研究[D]. 扬州: 扬州大学, 2008. ZHOU Weiming. Experimental study on energy dissipation hinge of different yield reinforcement concrete structure[D]. Yangzhou: Yangzhou University, 2008.
[21]	车轶, 王金金, 郑新丰, 等. 反复荷载作用下高强混凝土梁受弯性能尺寸效应试验研究[J]. 建筑结构学报, 2013, 34(8): 100-106. CHE Yi, WANG Jinjin, ZHENG Xinfeng, et al. Experimental study on size effect of flexural behavior of reinforced high-strength concrete beams subjected to cyclic loading[J]. Journal of Building Structures, 2013, 34(8): 100-106. DOI:10.14006/j.jzjgxb.2013.08.012
[22]	COOPER M, DAVIDSON B, INGHAM J. The influence of axial compression on the elongation of plastic hinges in reinforced concrete beams[C]//The New Zealand Concrete Industry Conference. Auckland: [s. n. ], 2005.
[23]	杨彦芳. 低周反复荷载作用下联肢剪力墙中连梁的强度及抗震性能的试验研究[D]. 重庆: 重庆建筑大学, 1998. YANG Yanfang. Test and study of strength and aseismic behavior of reinforced concrete coupling beams between shear wall [D]. Chongqing: Chongqing Jianzhu University, 1998.
[24]	TASSIOS T P, MORETTI M, BEZAS A. On the behavior and ductility of reinforced concrete coupling beams of shear walls[J]. ACI Structural Journal, 1996, 93(6): 711-720.
[25]	刘光伟. 小跨高比剪力墙洞口连梁抗震性能试验研究[D]. 重庆: 重庆大学, 2006. LIU Guangwei. Experimental study on seismic behavior of short-span coupling beams of shear walls [D]. Chongqing: Chongqing University, 2006.
[26]	杨程. CRB550级箍筋混凝土梁的抗震性能对比试验研究[D]. 广州: 华南理工大学, 2010. YANG Cheng. Comparing experimental research on earthquake-resistant behavior of reinforced concrete beams with CRB550 stirrups[D]. Guangzhou: South China University of Technology, 2010.
[27]	龚涣钧. RC梁、柱构件变形性能指标限值试验研究[D]. 广州: 华南理工大学, 2016. GONG Huanjun. Experimental research on deformation limits of RC beam and column [D]. Guangzhou: South China University of Technology, 2016.
[28]	高层建筑混凝土结构技术规程: JGJ 3—2010 [S]. 北京: 中国建筑工业出版社, 2010. Technical specification for concrete structures of tall building: JGJ 3—2010 [S]. Beijing: China Architecture & Building Press, 2010.
[29]	钱稼茹, 冯宝锐. 钢筋混凝土柱弯矩-转角骨架线特征点及性能点转角研究[J]. 建筑结构学报, 2014, 35(11): 10-19. QIAN Jiaru, FENG Baorui. Study on rotation angles at characteristic point and performance point of M-θ skeleton curve for RC columns[J]. Journal of Building Structures, 2014, 35(11): 10-19. DOI:10.14006/j.jzjgxb.2014.11.002
[30]	戚永乐. 基于材料应变的RC梁、柱及剪力墙构件抗震性能指标限值研究[D]. 广州: 华南理工大学, 2012. QI Yongle. Research on deformation limits of RC beams, columns and shear walls based on material strain [D]. Guangzhou: South China University of Technology, 2012.
[31]	SEZEN H, MOEHLE J P. Shear strength model for lightly reinforced concrete columns[J]. Journal of Structural Engineering, 2004, 130(11): 1692-1703. DOI:10.1061/(ASCE)0733-9445(2004)130:11(1692)
[32]	GHANNOUM W M, MATAMOROSA B. Nonlinear modeling parameters and acceptance criteria for concrete columns[J]. ACI Special Publication, 2014, 297(1): 1-24.
[33]	Seismic evaluation and retrofit of existing buildings: ASCE/SEI 41-13[S]. Reston, Virginia: American Society of Civil Engineers, 2014.
[34]	Applied Technology Council. Seismic performance assessment of buildings, Volume 1—Methodology: FEMA P-58-1[R]. California: FEMA, 2012.
[35]	韩小雷, 崔济东, 龚涣钧, 等. 不同抗震等级RC梁抗震性能试验研究[J]. 建筑结构学报, 2015(增刊2): 299-308. HAN Xiaolei, CUI Jidong, GONG Huanjun, et al. Experimental study on seismic behavior of RC beams with different seismic grades[J]. Journal of Building Structures, 2015(s2): 299-308. DOI:10.14006/j.jzjgxb.2015.S2.044