2. 哈尔滨工业大学 建筑设计研究院,哈尔滨 150090;
3. 太原万科房地产有限公司,太原 030006
2. Architecture Design and Research Institute of HIT, Harbin 150090, China;
3. Taiyuan Vanke Real Estate Limited Company, Taiyuan 030006, China
自由曲面结构以丰富的建筑表现力近年来受到建筑师的青睐,同时也给结构工程师带来挑战;如何在符合建筑设计意图的前提下实现更加合理的曲面构形,是结构设计中迫切需要解决的问题[1].
由薄壳理论可知,曲面结构的理想受力状态是只有薄膜应力没有弯曲应力,即具有零弯矩特征.在前计算机时代,零弯矩曲面主要是通过模型试验或解析方法获得;近年来,基于计算机技术的零弯矩曲面数值找形方法逐渐受到重视.
本文首先介绍了模型试验法和解析法的原理与应用,然后借鉴膜结构找形技术,提出了基于动力松弛法的零弯矩自由曲面结构找形方法; 在此基础上,探讨了自由曲面结构的形状精确控制问题;最后通过对逆吊型、充气型和张拉型自由曲面结构的找形与受力分析,验证了方法的有效性.
1 试验找形法早在1675年,英国科学家胡克(R. Hooke)即发现"拱的合理形状与倒过来的悬索一致",这可以认为是对模型试验法的一种直觉认识.实际操作中依据对模型施加荷载方式的不同,模型试验法可分为3类:
1) 逆吊法.该方法是利用模型自重作为找形驱动力,获得结构合理构形.具体实施步骤为:先根据给定的边界和荷载条件,获得柔性结构在悬吊状态下的平衡构形;再通过对模型进行固化、翻转操作,获得在相应荷载作用下的纯压结构形式.20世纪初,西班牙建筑师A. Gaudi率先将该方法应用到建筑设计中,通过在一系列丝线上吊挂沙袋,并反复调整沙袋的重量和丝线的长度,获得所设想的建筑形状.他利用该方法设计了许多教堂建筑,图 1所示吉埃尔教堂便是其中的典型代表.

|
图 1 吉埃尔教堂 Figure 1 Guell Church |
20世纪中叶,瑞士工程师H. Isler对逆吊试验法做了进一步发展,探讨了多种可能的逆吊结构形状,设计并建造了多个混凝土薄壳结构.图 2所示分别为H. Isler设计的Deitingen加油站和Sicili工厂[3].

|
图 2 Isler设计的混凝土薄壳结构 Figure 2 RC shells designed by Isler |
2) 充气法.该方法是以建筑内部气压作为找形驱动力,通过调整内压和边界条件来获得合理结构形状.当结构矢跨比较小时,该方法可认为与逆吊试验法等效.充气试验法的优点是可以直接利用充气膜作为薄壳结构的施工模板.Isler[4]率先将该方法用于实际工程,设计了若干混凝土薄壳结构.图 3(a)为其设计的瑞士COOP中心.日本学者Kokawa[5]将该方法应用于冰壳结构的建造,见图 3(b).

|
图 3 利用充气试验法设计的典型建筑 Figure 3 Typical projects generated from pneumatic models |
3) 张拉法.该方法是利用预张力作为找形驱动力,获得具有负高斯曲率的薄壳形状.图 4(a)是德国建筑师F. Otto利用该方法设计的Stuttgart车站方案[6];图 4(b)为意大利工程师S. Musmeci设计的Basento高架桥[7].

|
图 4 张拉试验法的工程应用 Figure 4 Typical projects generated from tent models |
总的来看,模型试验法具有概念清晰、形象直观的特点,因而在前计算机时代发挥了重要作用;但由于试验相似律和量测精度等方面的制约,目前已较少在实际工程中应用.
2 解析找形法在薄壳结构找形的解析法方面,国外学者多采用图解静力学法.图解静力学是用图形绘制的方式,依据力的矢量图解关系,求解结构合理形态及内力的方法.图解静力学法基于两个图示:形图解和力图解.形图解是平衡状态下结构的形及外荷载在结构上的位置,力图解是外荷载与结构内力的矢量平衡,二者为互补关系[8].
图 5为利用图解静力学求纯压拱形态的基本算例.其过程为:将作用在结构上的外荷载简化为一系列竖向分布的力向量,对力向量编号并首尾相连,形成图 5(b)所示外力线;然后绘制原点,并依次与各力向量的首、尾相连,形成一系列的三角形,这些三角形组成的图形就是力图解.力图解中的三角形是力多边形,描述结构中外力作用点的平衡关系,原点与外力矢量连线的长度表示相应结构单元的内力值,方向表示单元在纯拉状态下的方向,这样由力图解便可绘制出外荷载作用下结构的纯拉形态(图 5(c)).最后,将纯拉形态翻转,获得图 5(d)所示纯压拱形态.

|
图 5 图解静力学法示意 Figure 5 Scheme of graphic statics |
图解静力学法操作简单,"形"与"力"的关系明确,在19世纪晚期至20世纪中叶曾盛行于欧美.图 6(a)为建筑师R. Guastavino利用图解静力学法设计的纽约市政地铁站[9],图 6(b)为A. Gaudi设计的奎尔公园挡土墙与廊柱[8].

|
图 6 图解静力学法工程应用 Figure 6 Typical projects generated from graphic statics |
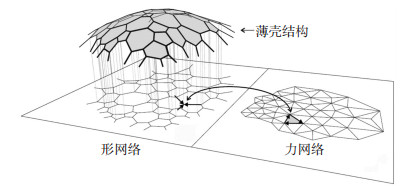
近年来,Block等[10]将图解静力学拓展到三维空间,提出了推力网格法,其原理与图解静力学相似,也是基于两个互补的图示:形网格和力网格.形网格是薄壳结构在水平面上垂直投影形成的网格,力网格是结构内力水平分量的矢量平衡关系.首先通过形网格和力网格的对应关系,获得薄壳结构在二维空间的合理形态,然后利用线性优化算法结合外荷载数值对可行解优化,最终求得结构三维空间的纯压构型,见图 7.推力网格法的出现为自由曲面薄壳结构分析提供了新思路.
|
图 7 推力网格法示意 Figure 7 Scheme of thrust network method |
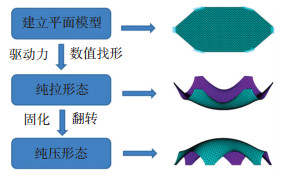
数值找形法是借鉴模型试验法的思想,在给定几何约束和边界支承条件下,利用数值方法模拟柔性索、膜结构在找形驱动力(自重、内压和预张力)作用下的平衡构形,从而获得受力合理的自由曲面结构形式.以数值逆吊法为例,图 8给出了薄壳结构数值找形流程图.
|
图 8 数值找形流程图 Figure 8 Flowchart of numerical form finding |
可以看出,上述数值找形过程与以往研究较多的膜结构找形十分相似,因此可以利用一些已有的膜结构找形方法,如力密度法、非线性有限元法和动力松弛法等[11].但是零弯矩自由曲面结构的数值找形方法并不等同于膜结构找形方法.因为,膜结构找形是以找到在给定边界和荷载条件下的结构平衡构形为目标;而自由曲面结构找形的目的是找到一个符合建筑要求的纯拉曲面,采用膜单元不过是一种手段,而且不需要采用真实数值,只要通过调整结构参数(如支承条件、荷载分布、材料属性等)获得满足建筑要求的结构形态即可.
在这方面,作者已针对逆吊型自由曲面结构进行了一些探索[2],本文将在此基础上引入动力松弛法,并将方法推广到充气型和张拉型自由曲面结构中,从而使方法的计算效率更高,适用范围更广.
3.2 动力松弛法动力松弛法是20世纪60年代英国工程师Day A.S.提出的一种求解非线性问题的数值方法.经过Barnes M.R.等的研究和发展,已广泛应用于索网及膜结构的找形中[12].
动力松弛法的基本原理是,将结构离散为单元和结点,在假定的初始形状下给定应力分布,形成结构内的不平衡力,在不平衡力的驱动下结构会产生运动(假定系统阻尼为零);当体系的动能达到最大值时,表明结构接近平衡位置,此时将所有结点速度设为零(相当于施加了人工阻尼);结构在新的位置重新开始运动,重复上述过程,直到不平衡力极小,达到静力平衡状态.
动力松弛法的计算流程为:建立初始几何模型,体系质量m集中在结点上,结点上外力和相关单元内力产生的结点不平衡力R将引起结点振荡.根据牛顿第二定律可得t时刻结点k在x方向的加速度a:
| $ R_{kx}^t = {m_k} \times a_x^t, $ | (1) |
将式(1)表示为中心差分形式:
| $ R_{kx}^t = {m_k}\left( {v_{kx}^{t + \frac{{\Delta t}}{2}} - v_{kx}^{t - \frac{{\Delta t}}{2}}} \right)/\Delta t. $ | (2) |
式中:Δt表示时间积分步长,v表示结点速度.
由式(2)可推导t+Δt/2时刻结点k在x方向的速度公式为
| $ v_{kx}^{t + \frac{{\Delta t}}{2}} = v_{kx}^{t - \frac{{\Delta t}}{2}} + R_{kx}^t \times \Delta t/{m_k}, $ | (3) |
k结点在t+Δt时刻的x坐标为
| $ x_{kx}^{t + \Delta t} = x_{kx}^t + \Delta tv_{kx}^{t + \frac{{\Delta t}}{2}}. $ | (4) |
按照上述公式,对所有结点进行计算,可得到所有结点在t+Δt/2时刻各个方向的速度分量及t+Δt时刻的最新结点坐标.由新的结点坐标可以计算此时的结点不平衡力,检验是否满足给定精度,如果满足则求得最终平衡状态,退出迭代.
按照式(3)可计算t+Δt/2时刻所有结点在x、y、z(用i=1, 2, 3表示)方向的速度,假设结构内共有N个结点,则此时体系的总动能T为
| $ {T^{t + \Delta t/2}} = \sum\limits_{k = 1}^N {\sum\limits_{i = 1}^3 {{m_k}v_{ki}^2} } . $ | (5) |
如果t+Δt/2时刻的动能小于t-Δt/2时刻的动能,说明体系动能在t-Δt/2时刻达到极大值,将所有速度分量重置为0,从t+Δt时刻的结构形态开始重复上述过程,直到获得结构的静力平衡形态[12-13].
鉴于动力松弛法可以从任意假定的不平衡状态开始迭代得到平衡状态,不需要形成刚度矩阵,且便于处理各种复杂的边界条件,因此本文选择动力松弛法作为自由曲面结构找形的主要方法.
3.3 形状调控方法对于逆吊型自由曲面和充气型自由曲面,给定边界条件时,由于找形驱动力的不同,零弯矩自由曲面的形态在理论上有无数多个解.为了获得满足建筑设计要求的形状,需要使找形结果满足一定的控制条件.为此,本文引入局部线性化方法来实现对结构形状的精确控制.
设y=f(x)为单调函数,因变量y与自变量x之间为非线性关系.欲求因变量为y*时,自变量x的取值可通过以下步骤实现:
1) 令x=x0,计算函数y0=f(x0);
2) 再令x=x0+Δ,计算函数y=f(x0+Δ), Δ是自变量x的微小增量;
3) 利用式(6)确定x1的值:
| $ {x_1} = {x_0} + \frac{\Delta }{{f\left( {{x_0} + \Delta } \right) - f\left( {{x_0}} \right)}} \times \left( {{y^ * } - f\left( {{x_0}} \right)} \right), $ | (6) |
4) 令x=x1, 计算函数y1=f(x1);
5) 判断y1与y*的差值是否满足容差ε;
若满足容差要求,则输出找形结果;若不满足则利用式(7)继续迭代计算,直至满足容差要求.
| $ {x_{k + 1}} = {x_k} + \frac{\Delta }{{f\left( {{x_k} + \Delta } \right) - f\left( {{x_k}} \right)}} \times \left( {{y^ * } - f\left( {{x_k}} \right)} \right). $ | (7) |
零弯矩自由曲面找形时,因变量y通常为控制点坐标,自变量x为找形驱动力或单元弹性模量.
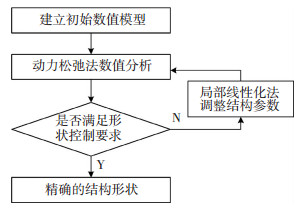
将局部线性化法与动力松弛法结合可以实现对结构特定目标点的控制,流程图如图 9所示.
|
图 9 精确控制基本流程 Figure 9 Basic process of form control |
当结构形状较为复杂时,需要进行多点精确控制,此时的找形思路如下:
1) 根据控制点的位置以及各单元与控制点的距离,将结构单元分组;
2) 利用单点控制程序对某一给定控制点进行找形分析,获得满足该控制点坐标要求的结构形态;
3) 将距离控制完成点近的那组单元的弹性模量放大为初始弹性模量的1×104倍,保证该控制点坐标在后续调控中几乎不发生变化;
4) 以此时的结构形态为初始形态,对下一个控制点进行调控;
5) 重复2)、3)、4)步骤,直至所有控制点的坐标均达到预定目标.
4 零弯矩曲面结构找形算例 4.1 算例1:逆吊型自由曲面荷兰代尔夫特理工大学的Borgart等[14]对H. Isler的大部分试验模型进行了3D扫描,本文选取其中某悬挂薄壳模型的点云数据,在Rhino中处理,得到图 10所示的NURBS拟合曲面.采用本文方法对其进行模拟,并将数值结果与试验结果对比,以验证本文方法的精确性.

|
图 10 Isler逆吊试验模型 Figure 10 Inverted hanging model of Isler |
图 11所示为平面初始模型,该模型为XY平面内的一个切角正方形,边长0.7 m,中心圆孔直径0.12 m,支承条件为四角固支.膜面均布荷载为50 N/m2.膜单元厚度0.001 m,泊松比0.3,经纬向弹性模量5×105 N/m2,不考虑剪切弹性模量的影响.

|
图 11 算例1平面初始模型 Figure 11 Initial form of example 1 |
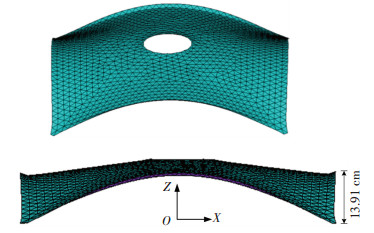
利用本文方法计算薄膜在重力作用下的平衡构形,设定内环控制高度为0.14 m,通过调整结点的重力荷载实现精确控制.找形过程中的控制点坐标变化曲线见图 12,最终找形结果见图 13.

|
图 12 精确控制过程 Figure 12 Process of form control |
|
图 13 精确控制结果 Figure 13 Result of form control |
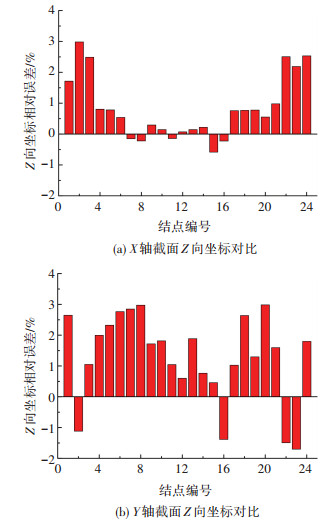
为验证找形结果的精度,在数值模型的X轴、Y轴截面上,分别均匀的选取24个点,位置及编号见图 11.将各点Z向坐标与Isler试验模型上对应点的坐标值进行比较,获得相对误差直方图(图 14).可以看出,靠近内环点的相对误差较小,而边缘区域的相对误差较大,但即便是最大相对误差也未超过3%,证明本文方法的精确性较高.
|
图 14 数值模型与物理模型对比 Figure 14 Comparison of numerical model and physical model |
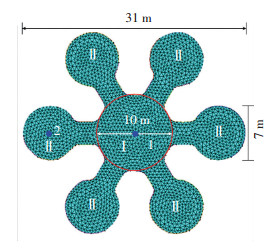
本算例的目的是说明多点精确控制的可行性.模型由7个圆形薄膜以及连接通道组成,总跨度31 m,中央充气膜跨度10 m,周边充气膜跨度7 m,通道长3.5 m.模型的支承条件为周边支承.
该模型进行充气找形,初始内压设为60 Pa,膜面预应力10 N/m,膜材参数同算例1.找形过程中未考虑自重的影响.通过调整膜内压来实现对结构形状的控制,具体流程如下:
1) 根据图 15中1、2控制点的位置,将模型单元划分为Ⅰ、Ⅱ两块区域,两区域相互独立,可设置不同内压值.
|
图 15 算例2初始模型 Figure 15 Initial model of example 2 |
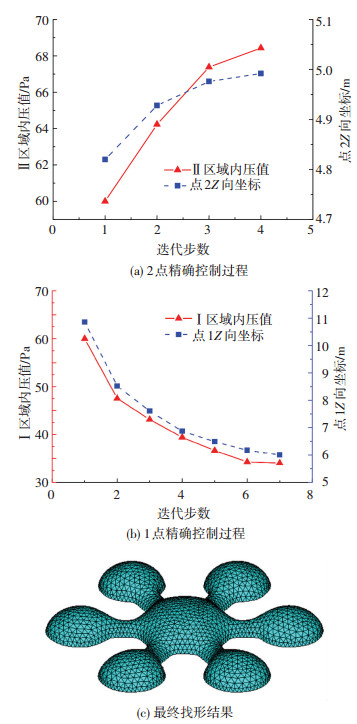
2) 利用局部线性化法调整内压值,使控制点2达到控制高度5 m,此时控制点1的高度为10.86 m,控制过程见图 16(a).
|
图 16 算例2精确控制结果 Figure 16 Form control result of example 2 |
3) 将Ⅱ区域单元的弹性模量放大为初始弹性模量的1×104倍,Ⅰ区域单元弹性模量保持不变.以此时的结构形态为初始形态,调整Ⅰ区域内压,使控制点1达到控制高度6 m.图 16(b)为点1控制过程,图 16(c)为调控后的模型形态.
需要说明的是,1点精确控制完成后,2点的高度为4.92 m,误差小于2%,精度满足要求.由上述结果可以看出,该方法控制过程简单,收敛速度较快,很好地解决了多点调控问题.
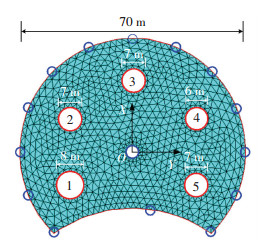
4.3 算例3:张拉型自由曲面建立如图 17所示张拉型曲面结构的初始模型,图中蓝圈内结点为固定支座,红圈为张拉环,按顺时针编号,张拉高度分别为11.5、11、10、9.5、10.5 m.膜材参数同算例1.
|
图 17 算例3初始模型 Figure 17 Initial model of example 3 |
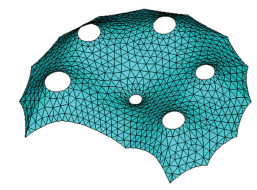
对初始模型进行张拉找形,预应力10 N/m.为保证计算收敛性,分800步将张拉环提升到指定高度.经过5 734次迭代后,得到了满足容差限值的平衡状态,见图 18.
|
图 18 算例3找形结果 Figure 18 Form-finding results of example 3 |
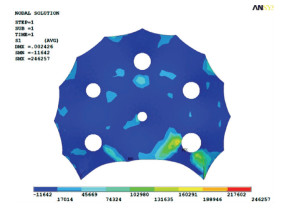
为验证找形结果的合理性,将膜材替换为混凝土材料,厚度取0.08 m,弹性模量2.06×1010 N/m2,密度2.5×103 kg/m3,对结构进行静力分析.分析时忽略自重的影响,仅在张拉端施加1×103 N/m的垂直荷载,结果见图 19.根据主应力云图可知,除极少数区域受拉外,薄壳结构可近似为纯压结构,受力十分合理.
|
图 19 算例3主应力云图 Figure 19 Principal stress of example 3 |
1) 借鉴模型试验法的思想,将自由曲面结构分为逆吊型、张拉型和充气型三类,引入动力松弛法进行找形分析,获得了受力合理的自由曲面结构形式.
2) 考虑到结构设计应满足建筑设计要求,引入局部线性化方法,通过调整结构的初始参数(支承条件、荷载分布、材料属性等),获得了满足建筑要求的自由曲面结构形态.
3) 通过对找形后结构进行荷载分析,证明了逆吊型自由曲面、张拉型自由曲面、充气型自由曲面均具有良好的力学性能.
| [1] |
沈世钊, 武岳. 结构形态学与现代空间结构[J]. 建筑结构学报, 2014, 35(4): 1-10. SHEN Shizhao, WU Yue. Structural morphology and modern space structures[J]. Journal of Building Structures, 2014, 35(4): 1-10. DOI:10.14006/j.jzjgxb.2014.04.003 |
| [2] |
武岳, 李清朋, 沈世钊. 基于逆吊试验原理的空间结构形态数值创建方法[J]. 建筑结构学报, 2014, 35(4): 41-48. WU Yue, LI Qingpeng, SHEN Shizhao. Computational morphogenesis method for space structures based on the principle of the inverse hanging experiment[J]. Journal of Building Structures, 2014, 35(4): 41-48. DOI:10.14006/j.jzjgxb.2014.04.006 |
| [3] |
ADRIAENSSENS S, BLOCK P, VEENENDAAL D, et al. Shell structures for architecture: form-finding and optimization[M]. London: Routledge Taylor and Francis, 2014.
|
| [4] |
ISLER H. New shapes for shells-twenty years after[J]. Bulletin of the International Association for Shell Structures, 1980, 72(3): 9-26. |
| [5] |
KOKAWA T. Buliding techniques for ice shell as temporary structure[C]//Proceedings of the IABSE-IASS Symposium. Seoul, Korea: [s. n. ], 2012.
|
| [6] |
温菲尔德·奈丁格. 轻型建筑与自然设计——弗雷·奥拓作品全集[M]. 柳美玉, 等译. 北京: 中国建筑工业出版社, 2010. NERDINGER W. Frei Otto complete works: lightweight construction, natural design[M]. Translated by LIU Meiyu, et al. Beijing: China Architecture & Building Press, 2010. |
| [7] |
IORI T, PORETTI S. The golden age of "Italian Style" engineering[C]//Proceedings of the Third International Congress on Construction History. Cottbus: [s. n. ], 2009.
|
| [8] |
孟宪川. 图解静力学的塑形法初探—关于形与力的生成关系研究[D]. 南京: 南京大学, 2014. MENG Xianchuan. Attempted morphing with Graphic Statics: a study on the form generating in force[D]. Nanjing: Nanjing University, 2014. |
| [9] |
RIPPMANN M. Funicular shell design[D]. Stuttgart: University of Stuttgart, 2016.
|
| [10] |
BLOCK P, OCHSENDORF J. Thrust network analysis: a new methodology for three-dimensional equilibrium[J]. Journal of the International Association for Shell and Spatial Structures, 2008, 48(3): 167-173. |
| [11] |
张建, 杨庆山, 李波. 气枕式充气膜结构形态与受力分析[J]. 哈尔滨工业大学学报, 2008, 40(12): 2020-2023. ZHANG Jian, YANG Qingshan, LI Bo. Form-state and loading analyses of air-flated cushion membrane structures[J]. Journal of Harbin Institute of Technology, 2008, 40(12): 2020-2023. DOI:10.3321/j.issn:0367-6234.2008.12.036 |
| [12] |
叶继红, 李爱群, 刘先明. 动力松弛法在索网结构形状确定中的应用[J]. 土木工程学报, 2002, 35(6): 14-19. YE Jihong, LI Aiqun, LIU Xianming. The application of the dynamic relaxation method in form-finding of the cable net structure[J]. China Civil Engineering Journal, 2002, 35(6): 14-19. DOI:10.3321/j.issn:1000-131X.2002.06.003 |
| [13] |
BARNES M R. Form finding and analysis of tension structures by dynamic relaxation[J]. International Journal of Space Structures, 1999, 14(2): 89-93. DOI:10.1260/0266351991494722 |
| [14] |
BORGART A, EIGENRAAM P. Scanning in 3D and analysing the models of Heinz Isler, the preliminary results[C]//Proceedings of the IABSE-IASS Symposium 2012. Seoul, Korea: [s. n. ], 2012.
|
 2018, Vol. 50
2018, Vol. 50


