引用本文

翟希梅, 戚仁平, 赵远征. 6082-T6铝合金构件受弯承载力计算方法[J]. 哈尔滨工业大学学报, 2018, 50(6): 192-198. DOI: 10.11918/j.issn.0367-6234.201705069.

ZHAI Ximei, QI Renping, ZHAO Yuanzheng. Calculation method of bending strength for 6082-T6 aluminum alloy beams[J]. Journal of Harbin Institute of Technology, 2018, 50(6): 192-198. DOI: 10.11918/j.issn.0367-6234.201705069.

基金项目

国家自然科学基金(51108126)

作者简介

翟希梅(1971—), 女, 教授, 博士生导师

通信作者

翟希梅, xmzhai@hit.edu.cn

文章历史

收稿日期: 2017-05-14

Abstract Full text Figures/Tables PDF

6082-T6铝合金构件受弯承载力计算方法

翟希梅^1,2, 戚仁平^1,2, 赵远征^1,2

1. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学)，哈尔滨 150090;
2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学)，哈尔滨 150090

收稿日期: 2017-05-14

基金项目: 国家自然科学基金(51108126)

作者简介: 翟希梅(1971—), 女, 教授, 博士生导师

通信作者: 翟希梅, xmzhai@hit.edu.cn

摘要: 为获得6082-T6铝合金箱型截面构件受弯承载力的计算方法，通过24个材性试验和19根箱型截面构件三点弯曲试验结果，在ABAQUS有限元模型获得弯曲试验结果验证的基础上，对468根铝合金三点弯曲构件进行数值模拟分析.鉴于现行美国、欧洲和中国铝合金设计规范在计算受弯构件的承载力时，均未考虑板组效应的影响，且计算过程繁琐，结果相对保守，针对6082-T6铝合金箱型截面受弯构件，基于直接强度法，提出了考虑材料非线性特征和构件初始缺陷的受弯承载力计算方法.最后，将本文提出方法的计算结果与试验数据及各国规范计算结果进行对比，结果表明：本文提出的计算方法具有较高精度，且使用简便，可较好预测6082-T6铝合金箱型截面三点弯曲构件的受弯承载力.

关键词: 铝合金受弯构件有限元分析受弯承载力直接强度法

Calculation method of bending strength for 6082-T6 aluminum alloy beams

ZHAI Ximei^1,2, QI Renping^1,2, ZHAO Yuanzheng^1,2

1. Key Laboratory of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090, China;
2. Key Laboratory of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090, China

Abstract: To predict the bending strength of 6082-T6 aluminum alloy flexural members, experimental studies of 24 tensile coupon tests and 19 three-point bending tests of box-section were performed. Finite element models using ABAQUS were developed and verified against the test results of 19 beams, and then used to perform parametric studies, in which a total of 468 numerical results were generated. The experimental and numerical results were used to evaluate the bending resistance provisions of the current American, European and Chinese Specifications. The impact of plate-assembly effect was not considered in these three specifications, which made the calculating process lightly complicated and the results relatively conservative. Based on direct strength method, the calculation method of bending strength considering the material nonlinear characteristics and initial geometric imperfection was proposed for 6082-T6 aluminum alloy bending members with box-section. Compared with the results of experimental data and three design specifications, it shows that the proposed calculation method is more accurate and convenient in predicting the bearing capacity of 6082-T6 aluminum alloy three-point bending beams of box-section.

Key words: aluminum alloy flexural member finite element analysis bending strength direct strength method

铝合金材料以其轻质、高强、可成型性好等优点被广泛应用于建筑领域.现行的美国铝合金设计手册^[1-2]、欧洲铝合金结构设计规范^[3]、中国铝合金结构设计规范^[4]均给出了受弯构件的设计方法，但上述方法均未考虑板组效应的影响.直接强度法(direct strength method，DSM)是Schafer等^[5]以有限条法为基础提出的冷弯薄壁型钢结构设计方法，该方法已被美国冷弯型钢规范(NAS 2004)^[6]和澳大利亚/新西兰铝合金结构设计规范(AS/NZS 1664.1)^[7]采用，文献[8-11]验证了修正后的直接强度法可适用于铝合金箱型截面轴压、偏压构件和四点弯曲构件；文献[12]采用系数折减法，也提出了铝合金圆管受弯构件的直接强度法计算公式.但目前，对于6082-T6铝合金箱型截面三点弯曲构件(受梯度弯矩)受弯承载力的直接强度法研究尚未进行.为此，本文首先进行19根6082-T6铝合金箱型截面构件的三点弯曲试验，并采用ABAQUS对其建立精细化的非线性有限元模型.根据模拟结果与试验结果的对比，验证了有限元模型的准确性和可靠性，并在此基础上对铝合金箱型梁进行扩大参数分析，共模拟了468个构件，包括12种宽度和高度，13种截面厚度，3种跨度.最后以本文试验与有限元分析结果为依据，对现行各国规范的计算方法、直接强度法以及本文提出的改进型直接强度法进行对比和验证.

1 铝合金受弯构件试验 1.1 6082-T6铝合金的本构关系

目前广泛使用的铝合金本构模型是Ramberg-Osgood模型：

$ \varepsilon = \frac{\sigma }{{{E_0}}} + 0.002{\left( {\frac{\sigma }{{{f_{0.2}}}}} \right)^n}. $

(1)

式中：E₀为材料原点处的弹性模量; f_0.2为名义屈服强度，取0.2%残余应变所对应的应力值；指数n是描述材料应变硬化的参数，取n=f_0.2/10^[13].

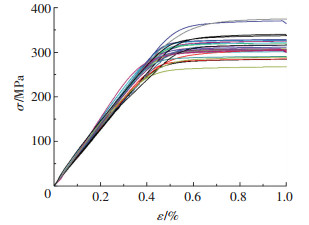
拉伸试验得到应力-应变曲线，见图 1.可以看出：6082-T6铝合金应力-应变曲线是一条连续光滑的曲线，没有明显的屈服平台，由于铝合金为挤压成型，力学性能指标具有一定的离散性.本文采用Shapiro-Wilk假设检验方法对弹性模量E₀、非比例延伸强度f_0.2、极限抗拉强度f_u的概率分布进行假设检验，得出在显著性水平α=0.05下，E₀、f_0.2、f_u均服从正态分布N(μ, σ²)的结论.本文另从文献[15]中搜集到了143条6082-T6铝合金应力应变曲线，共统计了167条实测应力应变曲线的力学性能参数，其弹性模量E₀、名义屈服强度f_0.2、极限抗拉强度f_u、断裂伸长率A_t和泊松比υ的平均值见表 1.

图 1 应力-应变曲线 Figure 1 Stress-strain curves

表 1 6082-T6铝合金力学性能参数 Table 1 Statistical parameters of mechanical properties for 6082-T6 aluminum alloy

1.2 铝合金受弯构件试验及结果分析

为研究两端简支的铝合金梁在跨中集中荷载作用下(三点受弯)的受力性能，共设计了9根SHS型截面(square hollow section)和10根RHS型截面(rectangle hollow section)试件，荷载作用于试件上翼缘.因铝合金构件并非理想直杆，初始缺陷对其受力性能有一定的影响，按文献[15]的方法对全部试件进行了初始缺陷测量.试件截面形状和尺寸汇总见表 2，以编号S1-80×80×6-2 000为例，S代表SHS型截面(R代表RHS型)；80×80×6-2 000分别代表构件截面的名义宽度、名义高度、名义壁厚和构件总长度L₀.

表 2 受弯试件汇总 Table 2 Sampling summary of bending specimens

构件编号	L₀/mm	L_e/mm	B/mm	H/mm	t/mm	B/t	λ_y	E₀/GPa	f_0.2/MPa	(D_imp/L₀)/‰
S1-80×80×6-2 000	2 000	1 800	79.9	79.9	6.03	13.25	59	63.0	296.5	0.68
S2-80×80×6-1 500	1 500	1 300	79.9	79.8	6.02	13.28	43	63.0	296.5	0.61
S3-80×80×6-1 200	1 200	1 000	79.9	79.9	5.95	13.42	33	63.0	296.5	0.43
S4-100×100×6-2 000	2 000	1 800	100.0	100.1	6.01	16.65	47	73.3	297.4	0.56
S5-100×100×6-1 700	1 700	1 500	100.0	99.9	6.02	16.62	39	73.3	297.4	1.72
S6-100×100×6-1 400	1 400	1 200	100.2	100.1	6.05	16.57	31	73.3	297.4	1.61
S7-100×100×8-2 700	2 700	2 500	100.4	100.1	8.01	12.53	66	58.3	270.3	0.49
S8-100×100×8-2 200	2 200	2 000	100.1	100.2	8.19	12.22	53	58.3	270.3	0.62
S9-100×100×8-1 700	1 700	1 500	100.1	100.0	8.14	12.30	40	58.3	270.3	0.64
R1-40×80×6-2 000	2 000	1 800	39.8	79.8	5.94	6.70	118	55.4	272.3	0.47
R2-40×80×6-1 700	1 700	1 500	39.9	79.7	5.91	6.75	98	55.4	272.3	0.80
R3-40×80×6-1 500	1 500	1 300	40.8	79.9	6.01	6.80	83	55.4	272.3	0.77
R4-40×80×6-1 200	1 200	1 000	39.8	79.7	5.92	6.72	66	55.4	272.3	0.78
R5-50×100×4-1 500	1 500	1 300	49.6	99.7	3.95	12.58	64	66.7	269.6	0.45
R6-50×100×4-1 200	1 200	1 000	49.6	99.7	3.92	12.66	49	66.7	269.6	0.52
R7-50×100×6-2 000	2 000	1 800	49.9	100.0	5.94	8.41	92	66.4	332.5	0.74
R8-50×100×6-1 700	1 700	1 500	50.0	99.8	5.88	8.51	76	66.4	332.5	0.27
R9-50×100×6-1 500	1 500	1 300	49.9	100.0	5.98	8.35	66	66.4	332.5	0.59
R10-50×100×6-1 200	1 200	1 000	49.7	99.8	5.92	8.39	51	66.4	332.5	0.63
注：L_e是构件计算长度，L_e=L₀-200 mm(因试件两端分别伸出支座100 mm)；B代表截面宽度；H代表截面高度；t代表截面厚度；D_imp代表初始缺陷幅值.

表 2 受弯试件汇总 Table 2 Sampling summary of bending specimens

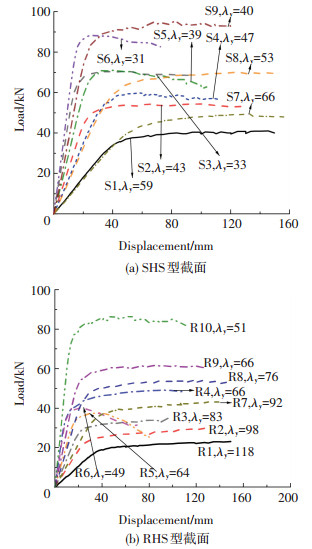
为保证梁端可以绕主轴方向自由弯曲，同时阻止梁端的侧向位移和扭转，设计了如图 2所示的支座.另外，在试件跨中设置钢制加载垫板，采用螺旋千斤顶施加集中荷载.试验后所有试件照片见图 3，荷载-跨中位移曲线见图 4.试件的受弯承载力结果和破坏模式见表 3.试验结果表明，构件破坏模式分两种：整体弯曲和局部屈曲的耦合破坏、整体弯曲破坏.对于SHS型截面试件，当绕弱轴长细比λ_y≤60($ {\lambda _{\rm{y}}} = {L_{\rm{e}}}/\sqrt {{I_{\rm{y}}}/A} $，I_y是绕弱轴惯性矩，A是净截面面积)时，构件的屈曲形式由局部与整体耦合屈曲控制，并且构件越短，局部屈曲起控制作用越强，整体弯曲发展越不充分，荷载下降段越明显，构件跨中位移越小，延性难以发展.当λ_y > 60时，构件的屈曲形式过渡到整体弯曲，在弹塑性阶段承载力会基本保持不变或缓慢增长，延性得到充分发挥.RHS型破坏规律与SHS型截面梁类似，但绕弱轴长细比分界大致以λ_y=60划分.当λ_y≤80时，构件发生局部屈曲和整体弯曲的耦合破坏，当λ_y > 80时，构件只发生整体弯曲破坏.

图 2 试验加载装置 Figure 2 Test set-up

图 3 试验后试件照片 Figure 3 Sample photos

图 4 试件荷载-跨中位移曲线 Figure 4 Load-mid-length displacement curves

表 3 试验和模拟结果对比 Table 3 Comparison of TEST and FEA results for alloy beams

构件编号	M_P/(kN·m)	M_EXP/(kN·m)	M_EXP	M_FEA/(kN·m)	M_EXP	破坏模式
构件编号	M_P/(kN·m)	M_EXP/(kN·m)	M_P	M_FEA/(kN·m)	M_FEA	破坏模式
S1-80×80×6-2 000	14.67	18.45	1.26	18.73	0.99	L+Y
S2-80×80×6-1 500	14.60	17.45	1.20	18.60	0.94	L+Y
S3-80×80×6-1 200	14.49	17.59	1.21	19.50	0.90	L+Y
S4-100×100×6-2 000	23.75	26.72	1.13	26.92	0.99	L+Y
S5-100×100×6-1 700	23.71	26.62	1.12	27.34	0.97	L+Y
S6-100×100×6-1 400	23.89	26.48	1.11	26.87	0.99	L+Y
S7-100×100×8-2 700	27.65	30.88	1.12	35.64	0.87	Y
S8-100×100×8-2 200	28.15	34.50	1.23	35.91	0.96	L+Y
S9-100×100×8-1 700	27.95	34.59	1.24	36.46	0.95	L+Y
R1-40×80×6-2 000	8.49	10.12	1.19	10.89	0.93	Y
R2-40×80×6-1 700	8.44	10.12	1.20	11.01	0.92	Y
R3-40×80×6-1 500	8.70	10.88	1.25	10.99	0.99	Y
R4-40×80×6-1 200	8.44	12.28	1.46	11.30	1.08	L+Y
R5-50×100×4-1 500	9.54	12.22	1.28	11.34	1.08	L+Y
R6-50×100×4-1 200	9.49	10.06	1.06	11.61	0.87	L+Y
R7-50×100×6-2 000	16.93	19.43	1.15	21.42	0.91	Y
R8-50×100×6-1 700	16.76	20.24	1.21	21.52	0.94	L+Y
R9-50×100×6-1 500	17.02	19.97	1.17	21.43	0.93	L+Y
R10-50×100×6-1 200	16.79	21.62	1.29	21.67	1.00	L+Y
注：L是局部屈曲破坏(local buckling)、Y是整体弯曲破坏(material yielding)；M_FEA是受弯承载力模拟值，M_FEA=P_FEAL_e/4，其中P_FEA是模拟得到的最大荷载；标准差的计算式为$ \sigma = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{x_i} - \mu } \right)}^2}} } $，其中N为数据个数，x_i为第i个数据值，μ为N个数据的平均值.

表 3 试验和模拟结果对比 Table 3 Comparison of TEST and FEA results for alloy beams

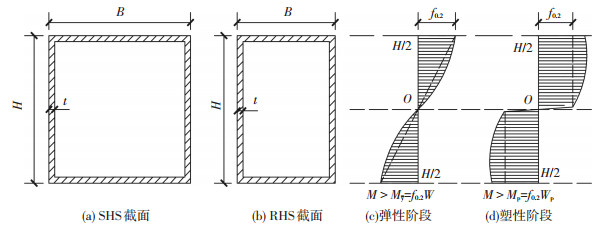
由表 3可知，M_EXP/M_p > 1(M_EXP是受弯承载力试验值，M_EXP=P_EXPL_e/4，P_EXP是试验中施加的最大荷载；M_p是截面塑性铰弯矩，M_p=W_pf_0.2，W_p为绕强轴的截面塑性模量)，即构件的受弯承载力大于梁截面的塑性铰弯矩，这主要是由铝合金材料截面的非线性特性导致的，主要表现在：(1)铝合金材料的比例极限较低，其后随应力的增加，应力沿截面高度分布呈非线性，如图 5(c)所示.当边缘应力达到f_0.2时，构件实际承受的弯矩大于图 5(c)虚线所示的屈服弯矩M_y(M_y = Wf_0.2，W为绕强轴的毛截面模量); (2)当截面边缘应力达到f_0.2后，材料进入应变硬化阶段，应力仍然持续增加；当中和轴附近应力达到f_0.2时，截面边缘应力已经超过f_0.2，构件承受的弯矩大于图 5(d)虚线所示的塑性铰弯矩M_p.

图 5 箱型截面的应力分布 Figure 5 Stress distribution of box-section

2 箱型截面受弯构件数值模拟 2.1 有限元模型建立

采用ABAQUS有限元软件对19根箱型截面试件进行数值模拟，所用构件尺寸均采用实测值.首先进行受弯构件的特征值屈曲分析，得到弹性范围内构件的低阶模态，选择一阶模态作为构件的初弯曲形状，并将其幅值调整为实测初始缺陷值；其次，采用弧长法进行非线性屈曲分析，得到构件的变形性能.对19根试件进行分析时，采用材料拉伸试验实测结果.扩大参数分析时采用材性试验均值，其中n=f_0.2/10=30.3.加载垫板材质为Q345钢材，本构模型采用理想的双折线模型.

铝合金构件采用S4R单元，即4节点减缩积分单元；钢制加载垫板采用C3D8R单元，即8节点三维减缩积分单元，边界条件为简支，加载方式为位移控制加载.由于网格尺寸的大小影响计算结果的精确性，本文选择了4种铝合金构件网格尺寸，分别为5、10、15、20 mm，分析网格尺寸对有限元受弯承载力的影响，结果表明：受弯承载力M_FEA随单元尺寸变小而有所增大，用10 mm和5 mm所得受弯承载力M_FEA相差小于3%左右.综合考虑计算结果的收敛性和耗时两方面因素，本文在有限元模型中采用10 mm网格对构件进行分析.

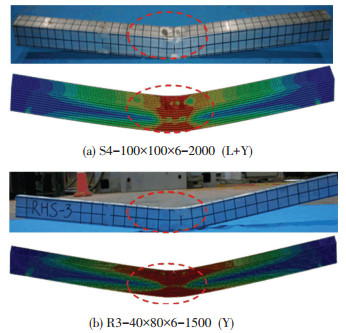
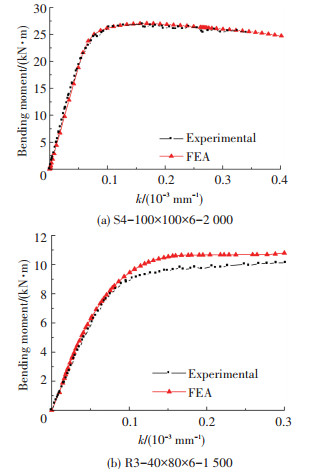
2.2 有限元模型分析与试验结果对比

数值模拟与试验关于受弯承载力及破坏模式的比较见表 3和图 6.图 7是S4-100×100×6-2 000和R3-40×80×6-1 500试件的弯矩-曲率曲线试验结果与模拟结果的对比图，可以看出：(1)模拟与试验结果在构件承载力与破坏模式两方面基本吻合；(2)模拟曲线和试验曲线走势基本一致，特别在上升阶段均吻合良好.总体而言，有限元模型在加载与破坏过程、破坏形式、受弯承载力与试验构件吻合良好，说明有限元模型在单元选取、参数设置、初始缺陷引入及网格划分等方面是可行的.

图 6 破坏模式的结果对比 Figure 6 Comparison of failure modes between test and FEA

图 7 弯矩-曲率曲线对比 Figure 7 Comparison of bending moment-curvature between test and FEA

2.3 参数设计与分析

本文参数分析包括468个构件，所采用的构件截面尺寸考虑到了几何参数的影响，根据现行欧洲规范EC9截面分类^[3]，为涵盖第一、第二、第三、第四类所有截面，宽厚比取值范围B/t是[3.3~100]，高厚比H/t范围是[3.3~200]，绕弱轴长细比λ_y范围是[11~217]，所有构件的初始缺陷幅值D_imp均为构件总长的1/1 000，具体参数设置见表 4，数值计算结果见图 8、9，图中M_n是各类设计方法得到的承载力计算结果.

表 4 参数设置 Table 4 Summary of the parameter setting

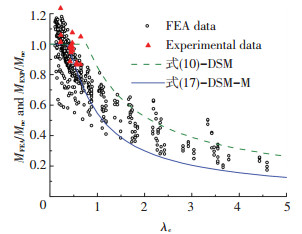
图 8 试验、有限元结果与DSM、DSM-M曲线比较 Figure 8 Comparison of test and FEA results with DSM, DSM-M curves

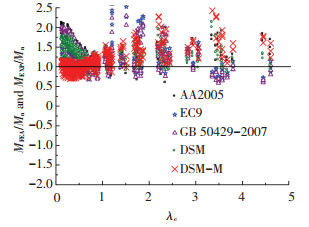
图 9 试验、有限元结果和各类设计方法比较 Figure 9 Comparison of tested and FEA results with different approaches

3 受弯构件承载力计算方法对比 3.1 美国铝合金设计手册(AA 2005)

AA 2005^[2]中许用应力设计法(ASD)和荷载抗力分项系数设计法(LRFD)均给出了铝合金箱型截面构件的抗弯承载力计算方法，LRFD只是将ASD中的许用应力和安全系数改成了极限强度设计值和抗力分项系数的形式，两者计算公式基本相同，可简化为

$ {M_{\rm{s}}} = S \times \min \left( {{f_{\rm{b}}},{f_{\rm{f}}},{f_{\rm{w}}}} \right). $

(2)

式中：S是对截面主轴的较小有效截面模量；f_b、f_f、f_w分别对应梁、翼缘、腹板受压的极限应力，与铝合金材料的加工状态、屈服强度及弹性模量、板件宽厚比等有关.

3.2 欧洲铝合金结构设计规范(EC9)

EC9^[3]采用有效厚度法，对于绕强轴受弯构件，截面的弯矩设计值应满足：

$ \frac{{{M_{{\rm{Ed}}}}}}{{{M_{{\rm{Rd}}}}}} \le 1.0, $

(3)

$ {M_{{\rm{Rd}}}} = \min \left( {{M_{{\rm{u,Rd}}}},{M_{{\rm{c,Rd}}}}} \right), $

(4)

$ {M_{{\rm{u,Rd}}}} = {W_{{\rm{net}}}}{f_{\rm{u}}}/{\gamma _{{\rm{M2}}}}, $

(5)

$ {M_{{\rm{c,Rd}}}} = \alpha {W_{{\rm{el}}}}{f_{\rm{o}}}/{\gamma _{{\rm{M1}}}}. $

(6)

式中：α是截面形状影响系数，与板件的宽厚比、材料的应变硬化、是否焊接、孔洞等因素有关；W_el是毛截面弹性模量；f_o是材料屈服强度；W_net是净截面弹性模量，应同时考虑孔洞、焊接热影响区等的影响；f_u是材料极限抗拉强度；γ_M1、γ_M2是分项修正系数，取γ_M1=1.10、γ_M2=1.25.

3.3 中国铝合金结构设计规范(GB 50429)

GB 50429 ^[4]采用有效厚度法，对于在主平面内受弯的构件，其抗弯强度计算式为

$ \frac{{{M_x}}}{{{\gamma _x}{W_{{\rm{en}}x}}}} + \frac{{{M_y}}}{{{\gamma _y}{W_{{\rm{en}}y}}}} \le f. $

(7)

式中：M_x、M_y是同一截面处绕x轴和y轴的弯矩；W_enx、W_eny是对截面主轴x轴和y轴的较小有效截面模量，应同时考虑局部屈曲、焊接热影响区以及截面孔洞的影响，采用有效厚度法对截面进行折减；γ_x、γ_y是截面塑性发展系数，对箱型截面，取γ_x=1.0、γ_y=1.0；f是铝合金材料的抗弯强度设计值.

3.4 直接强度法

直接强度法(DSM)原是一种针对开口截面的冷弯薄壁型钢构件设计方法^[5]，该方法以构件全截面为研究对象，同时考虑了构件的整体屈曲、局部屈曲和畸变屈曲以及局部屈曲与整体屈曲的相关性，只需预先求出考虑板组效应的构件弹性屈曲荷载，就能求出构件的受弯承载力，使得计算过程极大简化.受弯构件直接强度法计算公式，见式(8)~(11)所示，相关系数和破坏形式分界点等的取值均是根据冷弯型钢开口截面梁的试验数据拟合得到^[16].

$ {M_{{\rm{DSM}}}} = \min \left( {{M_{{\rm{ne}}}},{M_{{\rm{nc}}}},{M_{{\rm{nd}}}}} \right), $

(8)

$ {M_{{\rm{ne}}}} = \left\{ \begin{array}{l} {M_{{\rm{cre}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{M_{{\rm{cre}}}} < 0.56{M_{{\rm{\bar y}}}};\\ \frac{{10}}{9}{M_{{\rm{\bar y}}}}\left( {1 - \frac{{10{M_{{\rm{\bar y}}}}}}{{36{M_{{\rm{cre}}}}}}} \right),2.78{M_{{\rm{\bar y}}}} \ge {M_{{\rm{cre}}}} \ge 0.56{M_{{\rm{\bar y}}}};\\ {M_{{\rm{\bar y}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{M_{{\rm{cre}}}} > 2.78{M_{{\rm{\bar y}}}}. \end{array} \right. $

(9)

$ {M_{{\rm{nc}}}} = \left\{ \begin{array}{l} {M_{{\rm{ne}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{\rm{c}}} \le 0.776;\\ \left[ {1 - 0.15{{\left( {\frac{{{M_{{\rm{crc}}}}}}{{{M_{{\rm{ne}}}}}}} \right)}^{0.4}}} \right]{\left( {\frac{{{M_{{\rm{crc}}}}}}{{{M_{{\rm{ne}}}}}}} \right)^{0.4}}{M_{{\rm{ne}}}},{\lambda _{\rm{c}}} > 0.776. \end{array} \right. $

(10)

$ {M_{{\rm{nd}}}} = \left\{ \begin{array}{l} {M_{{\rm{ne}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{\rm{d}}} \le 0.561;\\ \left[ {1 - 0.25{{\left( {\frac{{{M_{{\rm{crd}}}}}}{{{M_{{\rm{ne}}}}}}} \right)}^{0.6}}} \right]{\left( {\frac{{{M_{{\rm{crd}}}}}}{{{M_{{\rm{ne}}}}}}} \right)^{0.6}}{M_{{\rm{ne}}}},{\lambda _{\rm{d}}} > 0.561. \end{array} \right. $

(11)

式中：M_y是截面边缘纤维屈服弯矩，M_y=Wf_0.2，f_0.2是材料的屈服强度，本文取材性拉伸试验得到的数值；W是绕强轴的毛截面模量；M_cre是临界弹性侧向扭转屈曲弯矩；M_ne为不考虑局部屈曲影响的受弯构件的整体屈曲承载力，对应中国规范的φ_bM_y，对于本文研究的箱型截面受弯构件，因未发生侧向扭转屈曲，则M_ne=M_y；M_crc是考虑板组效应的临界弹性局部屈曲弯矩，可根据有限元计算得到；M_crd是弹性畸变屈曲弯矩；$ {\lambda _{\rm{c}}} = \sqrt {{M_{{\rm{ne}}}}/{M_{{\rm{crc}}}}} ;{\lambda _{\rm{d}}} = \sqrt {{M_{{\rm{ne}}}}/{M_{{\rm{crd}}}}} $.

由于在试验和有限元分析中，本文研究的箱型截面受弯构件均未发生侧向扭转屈曲和畸变屈曲，借鉴直接强度法，提出了改进的直接强度计算方法(DSM-M)，公式表达如下：

$ {M_{{\rm{DSM}} - {\rm{M}}}} = \left( {{M_{{\rm{ne}}}},{M_{{\rm{nc}}}}} \right), $

(12)

$ {M_{{\rm{ne}}}} = a{M_{{\rm{\bar y}}}}, $

(13)

$ {M_{{\rm{ne}}}} = \left\{ \begin{array}{l} {M_{{\rm{ne}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{\rm{c}}} \le b;\\ c \times \left[ {1 - d{{\left( {\frac{{{M_{{\rm{crc}}}}}}{{{M_{{\rm{ne}}}}}}} \right)}^{\rm{e}}}} \right]{\left( {\frac{{{M_{{\rm{crc}}}}}}{{{M_{{\rm{ne}}}}}}} \right)^f}{M_{{\rm{ne}}}},{\lambda _{\rm{c}}} > b. \end{array} \right. $

(14)

式中a、b、c、d、e、f是待确定的系数和分界点.需要指出的是：在式(13)前加上系数a，是考虑到铝合金材料的非线性特征，当构件发生整体弯曲破坏时，其受弯承载力大于截面边缘屈服弯矩M_y.本文针对宽厚比B/t范围为3.3~100的6082-T6铝合金箱型截面三点弯曲构件的试验和有限元模拟数据，首先根据构件的破坏形式将数据分为两类，一类为只发生整体弯曲破坏的数据点，一类为发生局部屈曲和整体弯曲耦合破坏的数据点，并采用最小二乘法对数据点进行非线性拟合，获得了公式(13)、(14)中各系数和分界点的取值，本文提出的DSM-M具体表达形式：

$ {M_{{\rm{DSM}} - {\rm{M}}}} = \left( {{M_{{\rm{ne}}}},{M_{{\rm{nc}}}}} \right), $

(15)

$ {M_{{\rm{ne}}}} = 1.531{M_{{\rm{\bar y}}}}, $

(16)

$ {M_{{\rm{ne}}}} = \left\{ \begin{array}{l} {M_{{\rm{ne}}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{\rm{c}}} \le 0.350;\\ 0.808\left[ {1 - 0.201{{\left( {\frac{{{M_{{\rm{crc}}}}}}{{{M_{{\rm{ne}}}}}}} \right)}^{0.5}}} \right]{\left( {\frac{{{M_{{\rm{crc}}}}}}{{{M_{{\rm{ne}}}}}}} \right)^{0.5}}{M_{{\rm{ne}}}},{\lambda _{\rm{c}}} > 0.350. \end{array} \right. $

(17)

试验、数值计算结果和根据式(10)绘制的DSM曲线、式(17)绘制的DSM-M曲线的比较见图 8，可以看出19个试验数据分布在DSM-M曲线附近，绝大部分模拟点均高于DSM-M曲线.采用各国规范、DSM以及DSM-M对本文试验构件承载力的计算结果见表 5，468个参数分析的统计结果见表 6，19个试验点的M_EXP/M_DSM-M均值为1.084，标准差是0.100，468个模拟点的M_FEA/M_DSM-M均值为1.125，标准差是0.238，均低于按现行各国规范以及DSM公式的计算结果；各种设计方法的计算汇总见图 9，可见DSM-M计算结果更接近试验和模拟结果.综上所述：用DSM-M计算6082-T6铝合金箱型截面三点弯曲构件的受弯承载力是准确适用的.

表 5 试验值和各类设计方法计算结果比较 Table 5 Comparison of test results with the predicted values from different approaches

构件编号	M_EXP/(kN·m)	$ \frac{{{M_{{\rm{EXP}}}}}}{{{M_{{\rm{AA}}}}}} $	$ \frac{{{M_{{\rm{EXP}}}}}}{{{M_{{\rm{EC9}}}}}} $	$ \frac{{{M_{{\rm{EXP}}}}}}{{{M_{{\rm{GB}}}}}} $	$ \frac{{{M_{{\rm{EXP}}}}}}{{{M_{{\rm{DSM}}}}}} $	$ \frac{{{M_{{\rm{EXP}}}}}}{{{M_{{\rm{DSM - M}}}}}} $
S1-80×80×6-2 000	18.45	1.52	1.31	1.45	1.45	1.07
S2-80×80×6-1 500	17.45	1.45	1.25	1.38	1.38	1.02
S3-80×80×6-1 200	17.59	1.47	1.27	1.40	1.40	1.03
S4-100×100×6-2 000	26.72	1.46	1.24	1.34	1.34	1.06
S5-100×100×6-1 700	26.62	1.45	1.23	1.34	1.34	1.06
S6-100×100×6-1 400	26.48	1.43	1.22	1.32	1.32	1.05
S7-100×100×8-2 700	30.88	1.24	1.07	1.18	1.18	0.93
S8-100×100×8-2 200	34.50	1.37	1.17	1.30	1.30	1.03
S9-100×100×8-1 700	34.59	1.38	1.18	1.31	1.31	1.04
R1-40×80×6-2 000	10.12	1.55	1.25	1.47	1.47	1.01
R2-40×80×6-1 700	10.12	1.56	1.25	1.48	1.48	1.02
R3-40×80×6-1 500	10.88	1.62	1.31	1.54	1.54	1.06
R4-40×80×6-1 200	12.28	1.89	1.52	1.80	1.80	1.24
R5-50×100×4-1 500	12.22	1.69	1.41	1.61	1.61	1.39
R6-50×100×4-1 200	10.06	1.40	1.17	1.33	1.33	1.15
R7-50×100×6-2 000	19.43	1.55	1.26	1.47	1.47	1.06
R8-50×100×6-1 700	20.24	1.63	1.33	1.54	1.54	1.11
R9-50×100×6-1 500	19.97	1.58	1.29	1.50	1.50	1.09
R10-50×100×6-1 200	21.62	1.74	1.42	1.65	1.65	1.19
平均值		1.525	1.271	1.442	1.442	1.084
标准差		0.149	0.102	0.146	0.146	0.100

表 5 试验值和各类设计方法计算结果比较 Table 5 Comparison of test results with the predicted values from different approaches

表 6 参数分析的统计结果 Table 6 Statistical results of the finite element analysis

4 结论

1) 根据对本文材性试验结果及文献数据的统计，6082-T6铝合金材料力学性能参数为：E₀=69.146 GPa, f_0.2=302.9 MPa, f_u=330.9 MPa.

2) 由于铝合金材料具有非线性的应力应变关系，19根箱型截面铝合金三点弯曲试件的受弯承载力M_EXP大于梁截面的塑性铰弯矩M_p.对于SHS型截面试件，当λ_y≤60时，构件发生局部屈曲和整体弯曲的耦合破坏，当λ_y > 60时，构件只发生整体弯曲破坏；RHS型截面试件则以λ_y=80为分界线.

3) 考虑材料和几何非线性，采用S4R单元模拟两端简支的铝合金箱型截面三点弯曲构件，其有限元结果在构件荷载变形曲线、破坏模式和受弯承载力等方面与试验实测结果吻合良好.

4) 中、美、欧三国规范和直接强度法对6082-T6铝合金箱型截面受弯构件的承载力计算均偏于安全，其中美国规范最为保守.

5) 基于直接强度法，并考虑铝合金材料的非线性特征和构件的初始缺陷，提出了DSM-M计算方法，可以很好预测承受梯度弯矩的6082-T6铝合金箱型截面构件的受弯承载力.该方法计算简便，可将板组效应、局部屈曲与整体弯曲耦合作用对受弯承载力的影响考虑到计算结果当中.

参考文献

[1]	The Aluminium Association. Specification for aluminium structures[S]. Washington D C: The Aluminium Association, 1994.
[2]	The Aluminium Association. Aluminium design manual: specifications & guidelines for aluminium structures[S]. Washington D C: The Aluminium Association, 2005.
[3]	European Committee for Standardization. Eurocode 9, Design of aluminum structures: general structural rules: EN 1999-1-1[S]. Brussels: European Committee for Standardization, 2007.
[4]	铝合金结构设计规范: GB/T 50429—2007[S]. 北京: 中国计划出版社, 2007. Code for design of aluminium structures: GB/T 50429—2007[S]. Beijing: China Planning Press, 2007.
[5]	SCHAFER B W, PEKÖZ T. Direct strength prediction of cold-formed steel members using numerical elastic buckling solutions[C]// Fourteenth International Specialty Conference. Missouri: University of Missouri-Rolla, 1998: 69-76.
[6]	North American specification for the design of cold-formed steel structural members: NAS 2004[S]. Washington: American Iron and Steel Institute, 2004.
[7]	Standards Australia and Standards New Zealand. Australian/New Zealand standard aluminium structures: limit state design: AS/NZS 1664. 1[S]. Homebush/Wellington: Standards Australia/Standards New Zealand, 1997.
[8]	ZHU Jihua, YOUNG B. Aluminum alloy tubular columns—Part Ⅰ: Finite element modeling and test verification[J]. Thin-Walled Structures, 2006, 44(9): 961-968. DOI:10.1016/j.tws.2006.08.011
[9]	ZHU Jihua, YOUNG B. Aluminum alloy tubular columns—Part Ⅱ: Parametric study and design using direct strength method[J]. Thin-Walled Structures, 2006, 44(9): 969-985. DOI:10.1016/j.tws.2006.08.012
[10]	ZHU Jihua, YOUNG B. Experimental investigation of aluminum alloy thin-walled tubular members in combined compression and bending[J]. Journal of Structural Engineering, 2006, 132(12): 1955-1966. DOI:10.1061/(ASCE)0733-9445(2006)132:12(1955)
[11]	ZHU Jihua, YOUNG B. Design of aluminum alloy flexural members using direct strength method[J]. Journal of Structural Engineering, 2009, 135(5): 558-566. DOI:10.1061/(ASCE)ST.1943-541X.0000004
[12]	姜陆彬. 铝合金圆管受弯构件数值分析[J]. 安徽建筑, 2016, 23(3): 56-57. JIANG Lubin. Numerical analysis of flexural members of aluminum alloy round tubes[J]. Anhui Architecture, 2016, 23(3): 56-57.
[13]	STEINHARDT O. Aluminum constructions in civil engineering[J]. Aluminum, 1971, 47: 131-139.
[14]	王誉瑾. 6082-T6铝合金轴心受压构件稳定性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2015. WANG Yujin. Investigation on the stability of aluminum alloy 6082-T6 members in axial compression[D]. Harbin: Harbin Institute of Technology, 2015.
[15]	翟希梅, 孙丽娟, 赵远征. 高强铝合金压弯构件稳定承载力中欧规范对比[J]. 哈尔滨工业大学学报, 2013, 47(12): 1-8. ZHAI Ximei, SUN Lijuan, ZHAO Yuanzheng. Comparison of Chinese code and Eurocode9 in calculating the stability bearing capacity of high strength aluminum alloy beam-columns[J]. Journal of Harbin Institute of Technology, 2013, 47(12): 1-8. DOI:10.11918/j.issn.0367-6234.2015.12.001
[16]	SCHAFER B W. Review: the direct strength method of cold-formed steel member design[J]. Journal of Constructional Steel Research, 2008, 64(7): 766-778. DOI:10.1016/j.jcsr.2008.01.022