超声辅助抛光(ultrasonic-assisted polishing,UAP)为超声振动和其他传统抛光相结合的前沿技术. UAP可明显提高抛光去除效率,有效提高加工精度,改善表面质量, 并能延长工具寿命[1-2]. Xu等[3-4]将超声振动技术运用到蓝宝石衬底的化学机械抛光(CMP)加工过程,从运动学以及超声空化等方面研究了超声振动对磨粒作用的影响,揭示了蓝宝石高效高质抛光的机理.超声辅助抛光机理复杂,许多学者对金属、熔石英玻璃和陶瓷等不同材料都进行了UAP实验研究[5-7]. Zhou等[8]研究了固结磨粒抛光盘UAP熔石英过程中液体和工具磨损的作用. Li等[9]提出有效抛光磨粒的概念,建立了硅片的超声辅助CMP去除率模型,阐明了抛光工艺参数的作用. UAP参数的影响过程复杂,除了超声波在抛光过程中空化气泡溃灭对材料产生空蚀效应外,超声波还可以通过强化扩散进而实现质量传递过程的控制,并且均相体系相界面的化学进程也得到加速[10].王国刚等[11]通过电脉冲空蚀实验研究空泡溃灭过程中的力学损伤行为,发现空化过程中周期内出现两次峰值且脉冲放电产生的冲击压和冲量随距金属表面不同距离而表现不同. Skoczypiec[12]对超声辅助电化学加工间隙内电解液压力流速和气相分数进行了数值仿真.
计算流体力学(CFD)仿真是从理论上研究流体空穴效应的主要手段[13-15].本文通过采用fluent软件对超声辅助抛光流场的绝对压强、流速、气含率等参数进行数值分析,特别对超声下有效加工区域、二次空化及驻波现象等规律进行探索和总结,旨在为后续实验研究提供参考,从而更有效地利用这些规律来优化工艺参数.
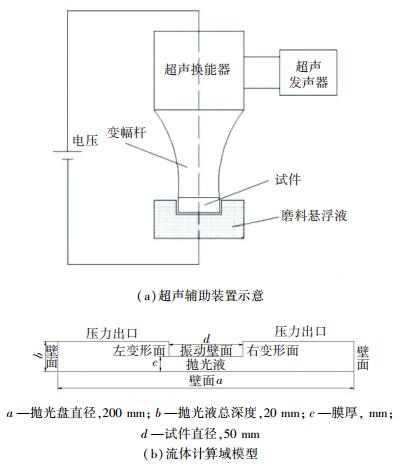
1 模型建立图 1为超声辅助抛光振动头及流场计算域模型结构图.考虑到流体为非稳态湍流,结合超声辅助抛光流场的特点选择多相流,调用mixture空化模型模拟空化作用. 表 1为Fluent调用的主要仿真模型及设置.
|
图 1 超声辅助装置及流场计算域 Figure 1 Ultrasonic device and flow field model |
| 表 1 Fluent主要参数设置 |
使用fluent前处理软件gambit建立二维模型,考虑到动网格对计算精度要求较高,因而选用非结构性三角形网格,划分为12 000单元.模型边界条件如图 1(b)所示:抛光液流场底面和两侧面为固定边界,随抛光头振动的试件下表面为振动壁面;振动壁面两侧为变形面,与空气接触的抛光液上界面为压力出口边界.
由超声振动参数,得出动边界的位移方程为
| $ y =-A\cos \left( {2\pi ft-\psi } \right). $ |
式中:A=30 μm;f为变量,Hz;t为振动时间,s;ψ为初相,π/2.为了便于编程,求导得出动边界速度方程为
| $ v = 2\pi fA\sin \left( {2\pi ft} \right). $ |
假设整个计算域绝热,没有热传导的作用;考虑重力,加速度g=-9.8 m/s2;室温下流体不可压缩气体质量分数初始值设为1.5×10-5.
2 有效加工区域及最小膜厚 2.1 有效加工区域取可控变量c=10.0 mm时的情况进行分析,即,试件随振头开始振动时对应膜厚c=10.0 mm,振动开始后膜厚为c±A.
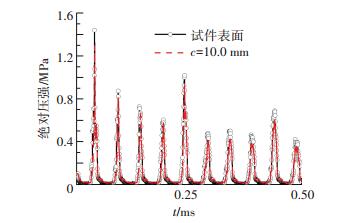
图 2为试件表面和c=10.0 mm平面处的绝对压强的对比曲线,两者不同之处在于前者是振动平面,后者平面是静止的.由图 2可知,振动表面的绝对压强略大于c=10.0 mm处的压强,整个时间域上,绝对压强曲线几乎完全重合,试件表面虽一直处于振动状态,但该区域的绝对压强却与c=10.0 mm平面处近乎相同.
|
图 2 绝对压强对比曲线 Figure 2 Curves of absolute pressure |
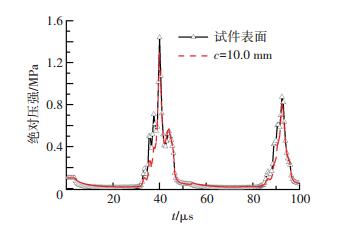
为了更清晰地观察两平面绝对压强的差异,选取如图 3所示任意两个周期的变化曲线,发现两者整体上基本一致.在局部略有差别是因为流场处于非稳态湍流状态,难免会出现微小的局部差异.
|
图 3 任意两周期绝对压强曲线 Figure 3 Absolute pressure curves of two cycles |
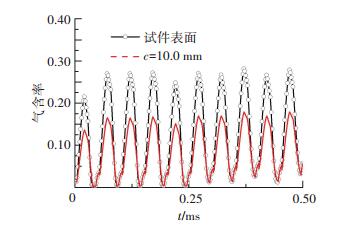
由图 4气含率随时间变化的曲线可知:试件表面气含率峰值28%,远高于c=10.0 mm区域处的15%,这是因为气核吸附在动壁面上,气泡更容易长大并发生溃灭,因此试件表面的气含率越高,则空化强度越强.
|
图 4 气含率对比曲线 Figure 4 Curves of vapour volume fraction |
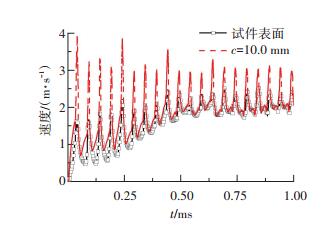
图 5为两平面速度随时间变化的曲线图,可以看出,c=10.0 mm处的流场流速(4.0 m/s)显著大于试件表面流场流速(1.5 m/s),速度曲线与绝对压强规律的显著差异,是因为试件与超声振动头作相同运动,速度是矢量,又因为试件表面流场流速为相对速度,因此其流速值较c=10.0 mm处的流速值有较为明显的下降.
|
图 5 速度对比曲线 Figure 5 Curves of velocity |
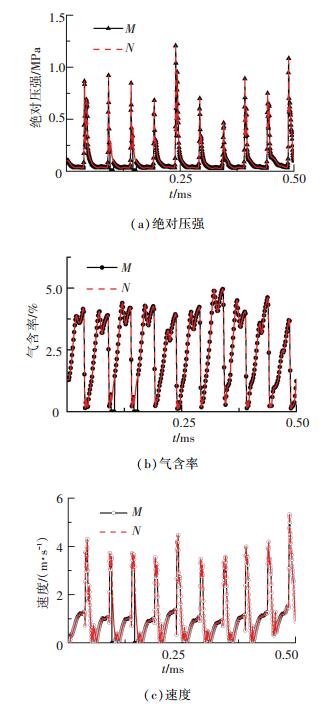
以上各曲线值均为面平均值,为消除其不确定性影响,选取中心轴的坐标点M(100.00 mm,10.00 mm)、N(100.00 mm,9.96 mm)并得到其参数曲线. 图 6(a)、(b)、(c)分别为M、N处绝对压强、速度、气含率数值曲线,由图 6可看出M、N点处各参数完全一致.证明流场中的参数在某一小范围区域内是相同的,并且中心轴上的M、N绝对压强和流速远大于c=10.0 mm面上的平均值,同时也证明了试件表面的中心区域是主要空化区域.
|
图 6 M、N点参数对比曲线 Figure 6 Contrast curves of M、N |
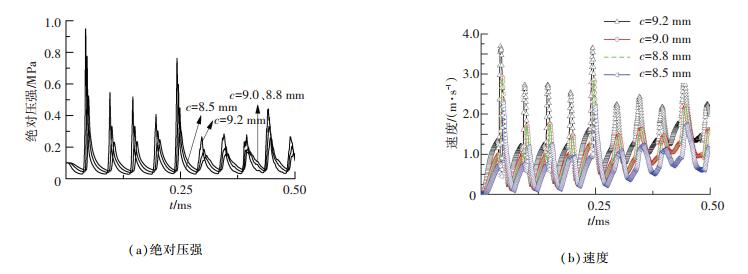
图 7(a)、(b)分别为试件正下方膜厚c=9.2、9.0、8.8、8.5 mm平面上的流体绝对压强和流速,两者均随距离试件表面的距离增大而减小,c=9.0和c=8.8 mm处绝对压强和流体流速完全重合,c=8.5 mm处相对其他面的值大幅度减小,因而对应c=10.0 mm工况,可得保持足够流场压力和速度的有效加工膜厚范围为c=8.8~10.0 mm,即振头下方1.2 mm的深度范围.
|
图 7 参数对比曲线 Figure 7 Contrast curves of parameters |
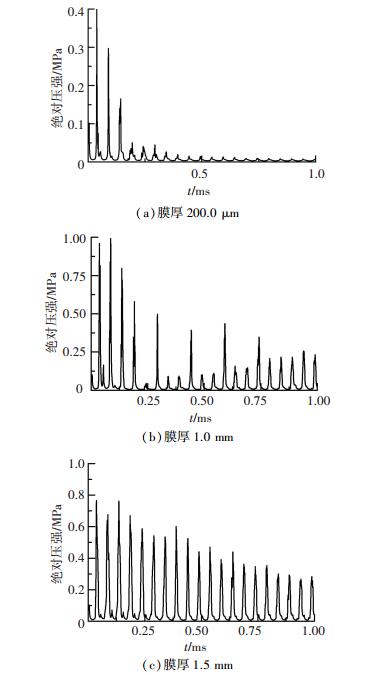
图 8(a)、(b)、(c)分别为抛光液流场膜厚200.0 μm、1.0 mm、1.5 mm时的试件表面处绝对压强变化图.
|
图 8 膜厚为200.0 μm、1.0 mm、1.5 mm时的绝对压强 Figure 8 Absolute pressure curves for slurry films of 200.0 μm、1.0 mm、1.5 mm |
由图 8可知:振动开始后,200.0 μm膜厚状态时, 流场绝对压强很快降低为约2.7 kPa; 1.0 mm膜厚状态时, 绝对压强峰值约为0.25 MPa,但有较大幅度波动; 1.5 mm膜厚状态时, 绝对压强维持在0.4 MPa,因此超声辅助加工方式对流场膜厚有一定的范围要求,即试件下方膜厚要充足,否则加工的效果会被显著削弱甚至消失.综合图 7结论可知:抛光盘中流场膜厚不应小于1.5 mm,否则超声振动效果无法充分实现.
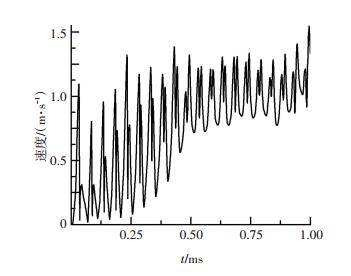
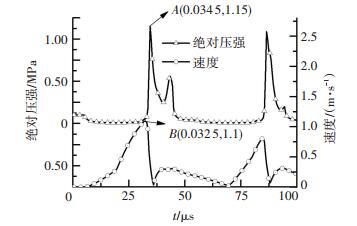
3 流场内若干现象分析 3.1 流场内的二次空化现象图 9为典型工况下流体速度变化.由图 9可知, 每周期速度都会出现两个峰值.并且随着流场充分稳定,速度二次峰值有逐渐增大的趋势.由图 10所示的两个周期内流速和绝对压强的对应曲线图可见,无论是流速还是绝对压强, 一个周期内都会出现两个峰值.
|
图 9 试件表面流体速度随时间分布曲线 Figure 9 Flow velocity curves of specimens |
|
图 10 绝对压强和速度随时间变化对比曲线 Figure 10 Curves of absolute pressure and velocity |
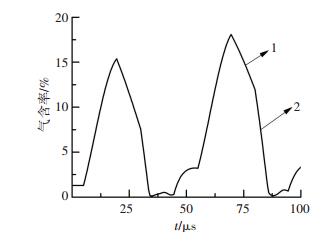
为进一步揭示两个峰值形成机理,结合图 11所示气含率随时间的分布曲线进行分析, 发现1、2两段线斜率不同. 1段斜率较小,对应首次空化,2段斜率较大,对应二次空化[11, 16],即二次空化气泡溃灭速率反而比首次空化还要大.说明超声辅助加工中产生的空化过程分为两个阶段,虽然第一阶段的气泡溃灭速率小于第二阶段,但第一阶段的空化压强和流体速率却显著大于第二阶段.这是由于首次空化会产生剧烈的微射流同时伴随大量的能量释放,使流场绝对压强和流速急剧增大,同时使二次空化随即发生,因而二次空化在加工过程中可发挥重要作用.
|
图 11 气含率随时间变化曲线 Figure 11 Curves of vapour volume fraction |
由图 10可知, 每个周期内,绝对压强和流场流速的峰值并非同时出现,观察到流速的峰值B出现在32.5 μs,而绝对压强的峰值A出现在34.5 μs,绝对压强的峰值滞后于流速峰值2.0 μs.这是由于试件表面的液体被振动壁面周期性冲击时,流速最先发生改变,当流速增大到一定值时,绝对压强才随之开始显著增大.因而流场周期计算域内,流体流速比绝对压强的变化更加“敏感”的原因是流体发生挤压后,才会产生绝对压强的突变.
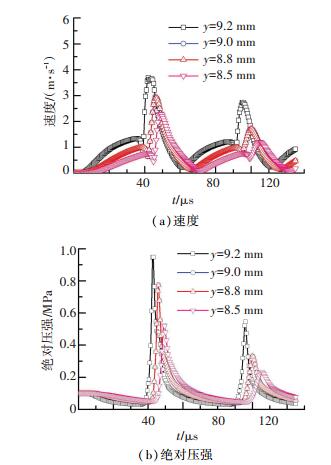
3.2.2 同一参量在不同位置的滞后选取c=9.2、9.0、8.8、8.5 mm等4个水平面,对绝对压强和流速均值进行记录,图 12(a)、(b)为两周期内的绝对压强和流速曲线.由图 12可知,无论是流速还是绝对压强都存在不同程度的滞后现象,c值越小即距离试件初始表面越远,峰值间滞后越明显,由于试件运动冲击抛光液,能量传递过程由近及远,因而抛光液参数变化需要“反应时间”,来实现流体加速和挤压过程.
|
图 12 速度和绝对压强曲线 Figure 12 Curves of velocity and absolute pressure |
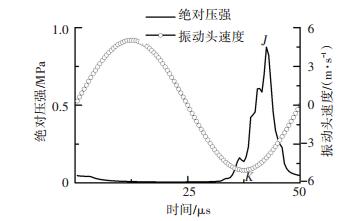
图 13为周期内绝对压强与超声振动壁面速度对比的曲线,K、J的横坐标分别为37.5和42.5 μs,超声振动壁面向下速度最大时,绝对压强并没有立即随之变为最大,而是有一定的延迟滞后,由于振动壁面以最大速度冲击流体时,完成挤压过程需要一定的时间,因而出现滞后现象.
|
图 13 绝对压强和振动头速度对比曲线 Figure 13 Curves of absolute pressure and vibration |
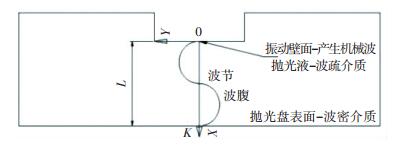
超声振动冲击流体产生机械波,并在流场中传递,遇到抛光盘底面时产生反射,形成相向传播的两列等振幅相干波,此时两波叠加形成驻波.由于机械波由波疏介质(抛光液)到波密介质(抛光盘)进行反射,产生半波损失,因而反射面即抛光盘表面处形成波节,此处振幅最小.如图 14所示,O为新建坐标系圆点,K为机械波反射点,OK=L.
|
图 14 驻波模型示意 Figure 14 Model of standing wave |
超声振动产生机械波,机械波随时间振动方程为
| $ {y_1} =- A\cos \left[{2\pi f\left( {t-\frac{x}{v}} \right)-\psi } \right], $ |
反射回去,经过半波损失后的K点振动方程为
| $ {y_p} =- A\cos \left[{2\pi f\left( {t-\frac{L}{v}} \right)-\psi + \pi } \right], $ | (1) |
将L= λ/4代和式(1)整理可得
| $ {y_p} =-A\cos \left( {2\pi ft} \right), $ | (2) |
则反射波的方程为
| $ {y_2} =- A\cos \left[{2\pi f\left( {t + \frac{{x-L}}{v}} \right.} \right]. $ | (3) |
叠加后的振动方程变为
| $ y = {y_1} + {y_2}. $ | (4) |
式中:A=30 μm;f=20 kHz;L为膜厚,mm;v为机械波传播速率,m/s;ψ为初相,ψ=π/2;考虑到膜厚既要尽可能减小,又要使试件表面处振幅尽可能最大,因而要保证O点是波腹位置,且L=λ/4时恰好可以实现试件表面为波腹位置,λ是机械波的波长.
由上述条件可知,叠加后O点的振动方程:
| $ y =-2A\cos \left( {2\pi ft-\frac{\pi }{2}} \right), $ | (5) |
| $ v = f \cdot \lambda . $ | (6) |
由式(2)~(5)可得:此时试件表面处的振幅变成2A,液体中机械波的传播速度约1 200~ 400 m/s,根据式(2)~(6)计算得到L=λ/4为15.0~17.5 mm,建立了膜厚为10~22 mm的系列模型进行流场仿真运算.
为了对比不同频率对流场特性的影响,定义绝对压强强度函数、速度强度函数以及气含率强度函数分别为
| $ {F_t} = \int\limits_0^t p \;\;{\rm{d}}t, \;\;\;\;\;\;{F_v} = \int\limits_0^t v \;\;\;{\rm{d}}t, \;\;\;\;\;\;\;{F_{{\rm{air}}}} = \int\limits_0^t a \;\;\;{\rm{d}}t. $ |
式中p为压强,Pa;定义Ft为绝对压强总强度, Pa·ms;v为速度,m/s;Fv为速度总强度,mm;a为气含率,Fair为气含率总强度,ms; t为流体域运行时间,ms.
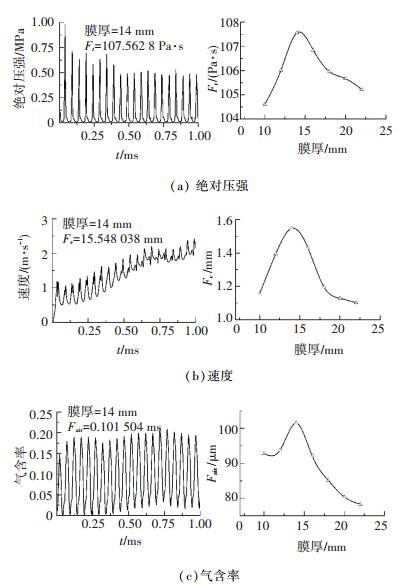
图 15(a)是膜厚14 mm(其余膜厚此处不再列举)时绝对压强曲线以及绝对压强强度曲线,同理可得速度以及气含率的相关曲线如图 15(b)、(c).由图 15可知:流场的主要参数包括绝对压强、速度、气含率均在流场膜厚为14.5 mm时取得最优值,进而推断此时试件表面附近为驻波的波腹位置,因此得到此时流体内机械波的理论波长是λ=58 mm,速度是v=1 160 m/s.当λ值不在查询值范围内时,a)超声空化效应干扰流场后,在气泡溃灭周期性发生过程中,大量微射流产生的能量使流场处于湍流状态,流场性质时时变化; b)除在底部发生反射外,还会伴有左右壁面反射的机械波干扰; c)由于流场流体成分复杂及不均匀分布的属性,因而抛光液具有向异性.
|
图 15 膜厚相关参数变化曲线 Figure 15 Curves of related parameters changing with film thickness |
1) 振幅A=30 μm,频率20 kHz时,有效加工区域为振头正下方1.2 mm的深度范围;振头所需膜厚最小为1.5 mm,否则流场加工性能将被减弱,超声无法充分发挥作用.
2) 流场绝对压强和速度周期性变化过程中,每周期都出现两次峰值,因而存在二次空化;滞后现象也体现在相同位置不同参量、相同参量不同位置、流场参量与超声振动上.
3) 当膜厚约为14.5 mm时,超声振动产生的机械纵波在流场中传递,由于半波损失和干涉而形成驻波可使试件表面处的机械波振幅最大,此时流场各特征参量取得最优值,振动辅助加工性能最好.
| [1] |
KOBAYASHI N, WU Y, NOMURA M, et al. Precision treatment of silicon wafer edge utilizing ultrasonically assisted polishing technique[J]. Journal of materials processing technology, 2008(201): 531-535. |
| [2] |
PRATEEK K, SUMIT K, PANDEY P M. Polishing of copper alloy using double disk ultrasonic assisted magnetic abrasive polishing[J]. Mater Manuf Process, 2013, 28(2): 200-206. DOI:10.1080/10426914.2012.746704 |
| [3] |
XU W, LU X, PAN G, et al. Ultrasonic flexural vibration assisted chemical mechanical polishing for sapphire substrate[J]. Applied Surface Science, 2010, 256(12): 3936-3940. DOI:10.1016/j.apsusc.2010.01.053 |
| [4] |
XU W, LU X, PAN G, et al. Effects of the ultrasonic flexural vibration on the interaction between the abrasive particles; pad and sapphire substrate during chemical mechanical polishing (CMP)[J]. Applied Surface Science, 2011, 257(7): 2905-2911. DOI:10.1016/j.apsusc.2010.10.088 |
| [5] |
TSAI M Y, YANG W Z. Combined ultrasonic vibration and chemical mechanical polishing of copper substrates[J]. International Journal of Machine Tools & Manufacture, 2012, 53: 69-76. |
| [6] |
LI Y, WU Y, ZHOU L. Vibration-assisted dry polishing of fused silica using a fixed-abrasive polisher[J]. International Journal of Machine Tools & Manufacture, 2014, 77: 93-102. |
| [7] |
ZHAO Q, SUN Z, GUO B. Material removal mechanism in ultrasonic vibration assisted polishing of micro cylindrical surface on SiC[J]. International Journal of Machine Tools & Manufacture, 2016, 103: 28-39. |
| [8] |
ZHOU C, ZHANG Q, HE C, et al. Function of liquid and tool wear in ultrasonic bound-abrasive polishing of fused silica with different polishing tools[J]. Optik, 2014, 125: 4064-4068. DOI:10.1016/j.ijleo.2014.01.113 |
| [9] |
LI L, HE Q, ZHENG M, et al. Contribution of ultrasonic traveling wave to chemical-mechanical polishing[J]. Ultrasonics, 2015, 56: 530-538. DOI:10.1016/j.ultras.2014.10.006 |
| [10] |
CRUN L A, MASON T J, REISSE J L, et al. Sonochemistry and Sonoluminescence[M]. [S.l.]: Kluwer Academic Publishers, 1999.
|
| [11] |
王国刚, 孙冬柏, 张秀丽, 等. 空泡溃灭过程中力学损伤行为[J]. 北京科技大学学报, 2007, 29(5): 483-485. WANG Guogang, SUN Dongbai, ZHANG Xiuli, et al. Dynamic impact behavior during bubble collapsing[J]. Journal of University of Science and Technology Beijing, 2007, 29(5): 483-485. |
| [12] |
SKOCZYPIEC S. Research on ultrasonically assisted electrochemical machining process[J]. Int J Adv Manuf Technol, 2011, 52: 565-574. DOI:10.1007/s00170-010-2774-4 |
| [13] |
罗经, 李健. 基于CFD的水轮机气蚀机制探讨[J]. 润滑与密封, 2006(7): 102-104. LUO Jing, LI Jian. Mechanism of cavitation erosion of the hydraulic turbine by CFD[J]. Lubrication Engineering, 2006(7): 102-104. |
| [14] |
孙冰, 张会臣. 基于CFD方法的超声空化发生特性数值分析[J]. 润滑与密封, 2009, 34(4): 55-60. SUN Bing, ZHANG Huichen. Numerical simulation of ultrasonic cavitation based on FLUENT[J]. Lubrication Engineering, 2009, 34(4): 55-60. |
| [15] |
SAJJADI B, RAMAN A A, IBRAHIM S. Influence of ultrasound power on acoustic streaming and micro-bubbles formations in a low frequency sono-reactor: Mathematical and 3D computational simulation[J]. Ultrasonics Sonochemistry, 2015, 24: 193-203. DOI:10.1016/j.ultsonch.2014.11.013 |
| [16] |
常敬忠. 超声辅助电化学机械抛光仿真与实验研究[D]. 哈尔滨: 哈尔滨工业大学, 2017. CHANG Jingzhong. Simulation and experimental study on ultrasonic assisted electrochemical machanical polishing[D]. Harbin: Harbin Institute of technology, 2017. |
 2018, Vol. 50
2018, Vol. 50


