生物质热压成型是生物质能源作为燃料应用的一种广泛而有效的方式,其对于缓解化石燃料枯竭所带来的能源短缺问题以及燃料燃烧造成的环境污染问题,具有重要意义[1].生物质热压成型分为开式和闭式两种成型方式.开式因其工作过程连续得到较广泛应用,但其成型过程存在成型燃料表面和芯部受力不均较严重的情况;而闭式成型方式由于在封闭成型模具内成型,其成型燃料表面和芯部受力不均现象较开式成型方式要大大减少,从而得到成型质量较好的燃料产品.所以闭式生物质热压成型成型过程的研究不仅具有理论意义,也具有经济等实用意义.
生物质资源储量的丰富性和生物质能源作为燃料的经济性和环保性使得生物质热压成型的研究越来越受到关注.高名旺[2]等假设生物质是连续固体,建立瞬态加热的热传导模型,并用ANSYS软件对不同加热情况下的木屑材料的温度场进行仿真,得出加热温度在300 ℃时木屑成型效果较好.武锦涛[3]等认为流动颗粒间存在一薄层气膜,颗粒间通过气膜传热.黄文迪[4]等指出颗粒与颗粒之间存在3种传热形式:颗粒与颗粒间辐射传热、颗粒与颗粒间接触导热以及通过颗粒与颗粒间气膜传热.孙亮[5]等通过对稻壳成型产品松弛密度进行建模分析,利用正交试验得出影响稻壳成型产品松弛密度的因素中加热温度影响最大,含水率次之,然后是成型压力.
从传热快慢和节约外部能源考虑,模具直径、保压时间等对传热可能存在影响.相关研究大多基于连续体假设从有限元角度对生物质进行宏观分析,定性分析居多,鲜有明确的优化指标. EDEM离散元软件基于颗粒尺度,可以对散体进行离散元分析.因此采用EDEM离散元软件不仅可以为生物质传热提供新的分析思路,也成为对成型工艺参数分析讨论从而达成节约能源目标的有效手段.
本文从传热的角度出发,基于EDEM离散元分析软件,从生物质颗粒尺度,创建闭式生物质热压成型过程中的接触模型和传热模型;然后,用C++编写与接触模型和传热模型相关的API接口程序;最后设置相关生物质及模具参数,利用EDEM用户自定义程序对生物质热压成型过程传热进行仿真,并对模具直径和保压时间参数进行分析.
1 成型过程及相关假设 1.1 成型过程闭式生物质热压成型是在成型过程中利用外部热源对成型模具进行加热使生物质内的木质素达到软化点从而压缩粘结成型的工艺[6].其相应的成型模具如图 1所示,由成型模具套筒、活塞压杆和活动出料挡板构成.

|
图 1 闭式生物质热压成型模具 Figure 1 Closed biomass thermo-compression formation die |
成型过程中模具套筒外壁受加热器加热作用.热压成型时,活动出料挡板处于封闭状态,生物质材料在高温模具中受热达到木质素软化点,并在外部活塞压杆的作用下被压紧实,生物质颗粒间由于软化木质素的粘结作用而彼此连接,最终成型为棒状生物质燃料块.热压成型完成后,活动出料挡板处于打开状态,成型的生物质燃料在压杆的作用下被推出模具.此后活塞压杆回退,进行下一次生物质物料填充,并循环进行压缩成型过程.
1.2 相关假设生物质热压成型过程由于既存在压缩变形又存在热量传递,使得其传热模型建立存在以下困难:
1) 接触模型建立的困难.生物质与生物质之间是颗粒接触,生物质与成型模具间接触是非连续颗粒介质与连续固体介质间的接触,接触方式复杂;生物质颗粒由压缩初始的弹性变形发展到压缩后期的大变形的塑形变形,变形复杂[7].
2) 热传递模型建立的困难.生物质成型过程的热传递采用之前的连续介质体假设模型与实际存在较大出入,需要建立新的颗粒体与颗粒体及颗粒体与几何体之间的热量传递模型;生物质颗粒在压缩过程中产生的不可恢复塑性变形,需将热传递模型建立在生物质塑形变形的接触模型上.
针对上述热传递模型建立的困难,为便于分析计算,本文所建立接触模型和传热模型基于实际生物质与成型模具的相关特征做如下假设:
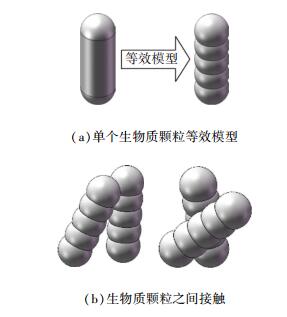
1) 生物质颗粒以实际生物质颗粒圆柱长条为模板,采用多球组合而成的多球面体做等效替代模型,如图 2(a)所示;生物质颗粒与颗粒间的接触为球面接触,如图 2(b)所示.
|
图 2 生物质颗粒模型 Figure 2 The model of biomass particle |
2) 成型模壁厚较薄,可假设模具温度为外部加热器所控制温度,且温度分布均匀.分析过程简化为恒温模具与生物质颗粒传热.
3) 实际生物质颗粒体为具有一定含水率的物料,不同含水率的物料参数存在差异,建模过程中将含水率等水分因素以参数的形式添加到颗粒体中.
4) 生物质颗粒和模具内壁微观表面实际为不平整的,为锯齿状边缘,为便于建模分析,将生物质颗粒表面和模具内壁假设为光滑的.
5) 生物质被粉碎后产生的颗粒较为细小,可以认为其Biot数足够小,不考虑单个生物质颗粒内部的热量传递情况,认为生物质颗粒在某一瞬时整个固体处于同一温度下.
2 接触模型的建立接触模型是EDEM软件进行仿真的关键,正确地设置仿真过程中的接触模型对仿真结果的准确性及可参考性具有重要意义. EDEM软件中颗粒体的模型有硬球模型和软球模型两种.硬球模型模拟的大多是颗粒间的瞬时碰撞,只考虑两个颗粒间的相互作用,多用于分析稀疏颗粒体间的碰撞运动;而软球模型模拟的可以是两个以上颗粒的碰撞问题,且其碰撞持续在一定时间内,其接触力根据颗粒交叠量由牛顿定律算出[8].
生物质颗粒在压缩过程中存在弹塑性变形,压缩变形过程复杂,采用软球颗粒体来模拟其成型过程.软球模型是把颗粒体接触过程中的运动和受力情况转化为弹簧恢复力和阻尼器的粘滞阻力综合作用下的运动情况[9].
EDEM软件中的Hysteretic spring模型将塑形变形引入到两颗粒体的接触过程中,事先给定两颗粒体接触间的接触极限力,当两颗粒接触变形还没达到预定值时,颗粒体间发生可恢复弹性变形,但是当颗粒体间接触变形达到预定的值时,颗粒体间发生屈服变形,之后颗粒体间发生不可恢复的塑形变形. Hysteretic spring模型与生物质压缩过程中颗粒体的接触变形及受力情况极为相似,所以生物质成型过程中的接触模型以Hysteretic spring模型为基础进行建立.
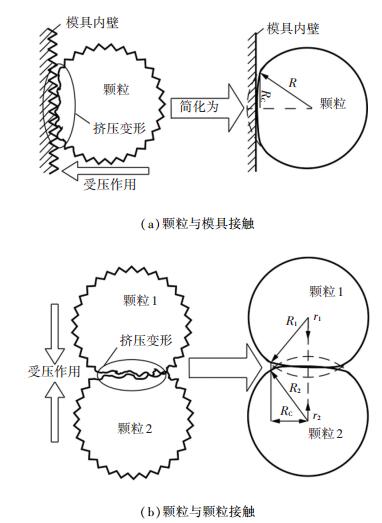
2.1 接触模型简化热传导模型中的接触模型主要有两种:1)颗粒体与颗粒体之间的接触模型;2)颗粒体与外部几何体之间的接触模型.颗粒体与颗粒体之间的接触模型如图 3(b)所示;颗粒体与几何体之间的接触模型如图 3(a)所示.
|
图 3 接触模型 Figure 3 Contact model |
当两颗粒间接触时,由前假设知,颗粒与颗粒间为球面接触,颗粒间接触的等效粒子半径为
| $ {R^*} = \frac{{{R_1} \cdot {R_2}}}{{{R_1} + {R_2}}}. $ |
当颗粒与模具接触时,相对于生物质颗粒来说,模具的体积要大很多.颗粒与模具接触可以相当于颗粒与半径无限大的球形几何体接触,颗粒与几何体之间的等效粒子半径为
| $ {R^*} = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} \approx {R_1}. $ |
式中R1, R2为两接触对象(包括颗粒与颗粒、颗粒与模具)的几何半径.
两接触对象间的接触面可以近似为圆形,其接触面的接触半径为
| $ {R_{\rm{C}}} = \sqrt {\alpha \cdot {R^*}} . $ |
式中α为两接触对象的法向接触重叠量[7],其表达式为
| $ \alpha = {R_1} + {R_2}-\left| {{r_1}-{r_2}} \right|. $ |
式中r1, r2为两接触对象的球心位置矢量.
2.2 接触力计算Hysteretic spring模型中两接触对象的接触点位置在彼此分离后不被记住,分离后的带有残余变形量的颗粒体与没有发生变形的颗粒体一样重新进行接触检索.模型中的接触力的计算如下.
法向力FN计算方式为[10]
| $ {F_{\rm{N}}} = \left\{ \begin{array}{l} {K_1}\alpha, \;\;\;\;\;\;\;\;\;\;\;\;\;{K_1}\alpha < {K_2}\left( {\alpha-{\alpha _0}} \right);\\ {K_2}\left( {\alpha-{\alpha _0}} \right), \;\;\;\alpha > {\alpha _0};\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \le {\alpha _0}. \end{array} \right. $ |
式中:K1表示加载刚度,K2表示卸载刚度,α0表示残余重叠量.
加载过程中的两接触对象在超过屈服极限后会产生相应的塑形变形,其中加载刚度与压缩过程中的接触对象的屈服强度有关,即
| $ {K_1} = 5{R^*}\min \left( {{\sigma _1}, {\sigma _2}} \right). $ |
式中σ1, σ2为接触对象的屈服强度.
接触对象在整个成型过程中的接触恢复系数由成型过程中的刚度决定:
| $ e = \sqrt {\frac{{{K_1}}}{{{K_2}}}} . $ |
成型过程中产生塑形变形后接触对象的残余重叠量在每个时间步内进行更新准则为
| $ {\alpha _0} = \left\{ \begin{array}{l} \alpha \left( {1-{K_1}/{K_2}} \right), \;\;\;\;\;\;{K_1}\alpha < {K_2}\left( {\alpha-{\alpha _0}} \right);\\ {\alpha _0}, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha > {\alpha _0};\\ \alpha, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \le {\alpha _0}. \end{array} \right. $ |
Hysteretic spring模型接触模型中的法向阻尼力计算方式为
| $ F_{\rm{N}}^{\rm{d}} =-b\sqrt {\frac{{4{m_{\rm{e}}}k}}{{1 + {{\left( {\frac{\pi }{{\ln e}}} \right)}^2}}}{v^{\rm{n}}}} . $ |
式中:k是K1或K2, b是无量纲比例阻尼系数,vn是相对速度法向分量,me为两接触对象的等效质量,按下式计算:
| $ {m_{\rm{e}}} = \frac{{{m_1}{m_2}}}{{{m_1} + {m_2}}}. $ |
Hysteretic spring接触模型的切向力计算基于线性弹簧弹性切向力的更一般的形式[11],其切向力计算如下:
| $ {F_{\rm{T}}} =-\min \left( {\gamma {K_1}\delta + F_{\rm{T}}^{\rm{d}}, \mu {F_{\rm{N}}}} \right). $ |
式中γ为无量纲刚度系数,δ为切向重叠量.
与法向阻尼力不同的是,切向阻尼力与阻尼系数并不成比例.
| $ F_{\rm{T}}^{\rm{d}} =-\sqrt {\frac{{4{m_{\rm{e}}}\gamma k}}{{1 + {{\left( {\frac{\pi }{{\ln e}}} \right)}^2}}}{v_{\rm{t}}}} . $ |
式中vt是相对速度法向分量.
3 传热模型建立成型过程中热量由模具的内壁传给与模具内壁直接接触的生物质颗粒薄层,然后再由生物质颗粒逐渐沿径向向成型燃料的轴心部分传递.热量传递过程相当于非稳态加热过程,随着温度升高,生物质材料中的木质素、纤维素等产生物理变化,甚至产生分解气体等化学反应,这使得传热过程较为复杂.为便于建模分析,本文忽略生物质热解反应的影响.
热量传递有热传导、热对流和热辐射三种基本方式.一方面,成型模具是固定的,生物质颗粒与模具周向没有相对运动,而只在压杆加压过程中生物质颗粒与模具轴向存在相对滑动,生物质颗粒在此过程中没有发生较为强烈的对流现象;另一方面,温度较低时辐射传热可以忽略不计,而生物质热压成型过程温度并不高.因此,生物质成型过程中热量传递主要考虑热传导形式.
成型过程中模具与生物质颗粒之间热量传递包括:模具内壁与近壁颗粒的热量传递;生物质颗粒与颗粒之间的热量传递.
3.1 颗粒与模具间传热生物质成型模具内壁微观表面并不平整,粉碎生物质颗粒微观表面也十分粗糙;生物质材料属性和模具材料属性差别较大,颗粒易发生塑形变形而模具不易发生塑形变形.因此,生物质颗粒在压缩过程中,并不会完全与模具内壁无缝隙接触.
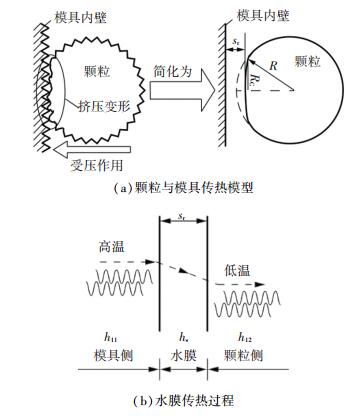
物料在回转容器中受热时,物料与回转容器间存在一层厚度不均的薄层气膜,容器通过气膜将热量传递给物料[12].但其所针对对象为容器内松散流动的颗粒物料,而生物质热压成型过程中有一定含水率的颗粒物料受压作用彼此间接触紧密,且颗粒间流动作用微弱,会导致在模具内壁面和近壁面颗粒存在着一层厚度不均匀的水膜.在研究颗粒物料与模具内壁面间的传热时,可认为模具内壁的热量传递由两部分组成:一部分是通过模具内壁面和近壁面颗粒的直接接触来实现的;另一部分是通过模具内壁面和近壁面颗粒之间的水膜来实现的,如图 4所示.简化分析,可分别计算两部分传热,然后取算术平均值.
|
图 4 颗粒与模具传热模型 Figure 4 Theheat transfer model of particle and die |
模具内壁和生物质颗粒的传热中,通过水膜实现的传热量表示为
| $ Q = \frac{{{\lambda _\rm{l}}}}{{{s_{\rm{r}}}}}\left( {{T_{\rm{s}}}-{T_{\rm{b}}}} \right)\pi R_{\rm{C}}^2. $ |
式中:sr为综合考虑模具内壁表面粗糙度和生物质颗粒表面外形不规则情况的接触间隙,将其值近似等效为水膜的厚度;λl为水膜的导热系数,Ts为模具内壁温度,Tb为颗粒温度.
可知水膜传热的传热系数为
| $ {h_{\rm{s}}} = \frac{Q}{{\pi R_{\rm{C}}^2\left( {{T_{\rm{s}}}-{T_{\rm{b}}}} \right)}} = \frac{{{\lambda _{\rm{l}}}}}{{{s_{\rm{r}}}}}. $ | (1) |
模具内壁与颗粒物料间通过水膜传热的传热系数为
| $ {h_{{\rm{ls}}}} = \frac{1}{{\frac{1}{{{h_{{\rm{l1}}}}}} + \frac{1}{{{h_{\rm{s}}}}} + \frac{1}{{{h_{12}}}}}}. $ | (2) |
式中hl1, hl2为水在成型挤压力下的对流换热系数.
另一方面,模具内壁面与颗粒体的接触传热系数计算方法为
| $ {h_{\rm{c}}} = \frac{{{k_{\rm{s}}}{k_{\rm{p}}}}}{{{k_{\rm{s}}} + {k_{\rm{p}}}}} = \frac{{{\lambda _{\rm{s}}} \cdot {\lambda _{\rm{p}}}}}{{{\lambda _{\rm{s}}}d + {\lambda _{\rm{p}}}\delta }}. $ | (3) |
式中:ks为模具的传热系数,kp为生物质颗粒体的传热系数,λs为模具的导热系数,d为生物质颗粒的横向直径,λp为生物质颗粒的导热系数,δ为模具的壁厚.
结合式(1)~(3),可得模具内壁与秸颗粒之间的总传热系数为
| $ \begin{array}{l} {h_{\rm{o}}} = \frac{{{h_{\rm{c}}} + {h_{\rm{s}}}}}{2} = \\ \;\;\;\;\;\;\frac{{{h_{{\rm{l1}}}}{\lambda _1}{h_{{\rm{l}}2}}\left( {{\lambda _{\rm{s}}}d + {\lambda _{\rm{p}}}\delta } \right) + 2{\lambda _{\rm{s}}}{\lambda _{\rm{p}}}\left( {{\lambda _{\rm{l}}}{h_{{\rm{l}}2}} + {h_{{\rm{l}}1}}{s_{\rm{r}}}{h_{{\rm{l}}2}} + {h_{{\rm{l}}1}}{\lambda _1}} \right)}}{{{\lambda _{\rm{l}}}{h_{{\rm{l}}2}} + {h_{{\rm{l}}1}}{s_{\rm{r}}}{h_{{\rm{l}}2}} + {h_{{\rm{l}}1}}{\lambda _{\rm{l}}}\left( {{\lambda _{\rm{s}}}d + {\lambda _{\rm{p}}}\delta } \right)}}. \end{array} $ |
生物质颗粒在压缩成型过程中受到较大的压力作用,颗粒与颗粒间接触变得非常紧密;且由于生物质颗粒材料极易发生塑形变形,所以在颗粒与颗粒接触时,认为颗粒与颗粒直接接触.此时,颗粒与颗粒间的接触传热占据主导地位.
Vargas[13]等发现固体床中颗粒接触传热的导热量计算公式为
| $ \frac{H}{{{\lambda _{\rm{s}}}}} = 2{\left( {\frac{{3{F_{\rm{N}}}{R^*}}}{{4{E^*}}}} \right)^{\frac{1}{3}}}, $ |
式中R*和E*为杨氏模量和当量半径.但其只针对于线弹性球形光滑颗粒发生完全弹性碰撞的情况.
生物质颗粒间直接接触传热同生物质颗粒与模具内壁接触传热相似,可以基于之前计算公式,则生物质颗粒间的传热系数为
| $ {h_{{\rm{cp}}}} = \frac{{{k_{{\rm{p1}}}}{k_{{\rm{p2}}}}}}{{{k_{{\rm{p1}}}} + {k_{{\rm{p2}}}}}} $ |
式中kp1、kp2为颗粒一与颗粒二的导热系数,kp1=kp2=kp.
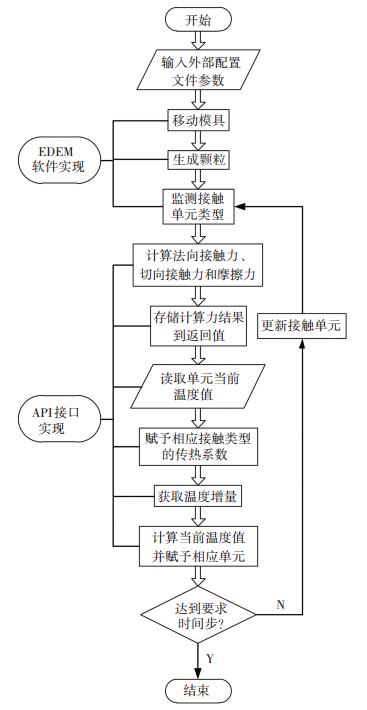
4 EDEM仿真实验 4.1 EDEM软件API接口编程EDEM软件良好的API接口为用户自定义颗粒属性、接触模型及颗粒体力等提供了便利,基于API接口类IPluginContactModel基类,建立新的接触模型子类继承基类相应的功能.编写基类中相应的计算力程序,程序中所用到的接触模型相关的函数及传热相关的函数均由之前所述的接触模型和传热模型给出. EDEM软件中API自定义接口程序编写思路如图 5所示.
|
图 5 EDEM-API编程思路 Figure 5 The framework of EDEM-API programming |
将所编写的EDEM的API接口程序用visual studio 2010编译后得到可以出现在EDEM软件面板的Windows配置文件,并将其添加到所创建的生物质颗粒体模型和模具几何体模型上,便可进行下一步仿真操作.
4.2 材料属性设置程序中所需的外部材料参数包括模具和生物质颗粒两部分.其中,模具材料为45钢;生物质材料因种类等差异导致其属性也存在差别,实际生物质粉碎颗粒的大小并不一致,但其大小分布近似服从正态分布,选取生物质颗粒为杆径1 mm,杆长3 mm的柱状体.模具和生物质材料相关参数属性设置如表 1所示[14].
| 表 1 材料属性设置 Table 1 The setting of material properties |
EDEM仿真中接触参数部分需要用户自定义设置,包括恢复系数、静摩擦系数和动摩擦系数等,其相关数值如表 2所示.
| 表 2 接触参数设置 Table 2 The setting of parameters of contact |
模具加热温度过低,生物质材料中的木质素没有达到软化温度,导致压缩过程颗粒间彼此粘结成型效果不佳;模具温度过高,不仅造成能源浪费,还易造成生物质表面炭化,使生物质燃料的燃烧值降低.为保证木质素软化,模具温度必须在其软化温度范围内选取,仿真中选取模具的加热温度为373 K,生物质颗粒的初始温度为298 K[15-16].
| 表 3 传热参数设置 Table 3 The setting of parameters of heat transfer |
生物质压缩成型过程中,随着压缩量的加大,生物质材料变得愈加紧密.针对成型直径为10 mm、壁厚2 mm及长度50 mm的模具,压缩量分别为0、12.5 mm(四分之行程)、25 mm(二分之行程)时做仿真实验分析. 图 6为3种压缩量下颗粒的温度分布情况.相同时间内,外部成型模具温度均为373 K时,传热速率关系为:25 mm压缩量传热>12.5 mm压缩量传热>0 mm压缩量传热.结果表明:随着压缩量的增加,生物质成型过程传热加快.这是由于压缩量增大时,生物质颗粒间接触面半径变大,使得接触传热面变大,相同时间内传递的热量增加.

|
图 6 不同压缩量下生物质颗粒温度分布 Figure 6 The temperature distribution of biomass particle under different compression |
EDEM传热仿真结果中生物质温度分布与文献[2]中有限元传热仿真结果中温度分布趋势基本一致,EDEM传热仿真结果具有一定的可靠性.由于EDEM传热仿真基于颗粒尺度,与有限元的宏观生物质分析相比,可以更方便地得到生物质散料局部乃至单个颗粒的温度变化情况,这对后续相关研究更具有指导意义.
4.5 模具直径对传热的影响不同直径的成型模具传热也存在差异,针对直径分别为10 mm、20 mm和30 mm的成型模具,在相同压缩量下(即使压缩后的体积保持一致)进行仿真. 图 7为3种成型模具直径下的生物质颗粒温度分布情况.成型模具直径从10 mm增加到30 mm,在体积不变的情况下,模具与生物质材料的宏观接触表面积增大,但燃料芯部温度却呈降低趋势.结果表明:随着模具直径增大,生物质颗粒的传热速率却降低.这可能是由于生物质传热相对较慢.

|
图 7 不同直径模具生物质颗粒温度分布 Figure 7 Thetemperature distribution of biomass particle under different diameter dies |
热压成型过程中保压时间过短,模具的热量还未传递到成型燃料的芯部,就会导致成型燃料表面和芯部质量好坏不均,易产生裂纹. 图 8为10 mm成型模具保压时颗粒温度变化,可知随着保压时间变长,生物质的温度逐渐升高.从保压时间角度出发,合理设置成型燃料在成型过程被压紧后的保型时间,对避免更换压力和加热温度条件,降低生物质成型成本和能源节约具有积极意义.

|
图 8 生物质颗粒温度分布 Figure 8 Thetemperature distribution of biomass particle |
1) 通过对10 mm直径成型模具在0 mm、12.5 mm及25 mm压缩量下进行EDEM仿真计算,得出:生物质热压成型过程传热速率随着压缩量的增大而增大.
2) 通过对直径10 mm、20 mm及30 mm的成型模具热压成型过程进行仿真计算,发现在相同的压缩体积下,随着成型模具直径增大,虽然模具与生物质材料的接触表面积变大,但生物质的传热速率却变得缓慢.
3) 生物质燃料成型过程的温度随着保压时间变长呈现升高趋势,合理设置保压时间有利于生物质木质素软化.
| [1] |
魏伟, 张绪坤. 生物质固体成型燃料的发展现状与前景展望[J]. 广东农业科学, 2012, 39(5): 135-138. WEI wei, ZHANG Xukun. Development status and prospect of solid biofuel-preparation in China[J]. Guangdong Agricultural Sciences, 2012, 39(5): 135-138. |
| [2] |
高名旺, 董玉平. 生物质热压成型温度场数值模拟[J]. 可再生能源, 2004(2): 23-25. GAO Mingwang, DONG Yuping. Numerical simulation of temperature field of biomass thermal compression[J]. Renewable Energy Resources, 2004(2): 23-25. |
| [3] |
武锦涛, 陈纪忠, 阳永荣. 移动床中颗粒接触传热的数学模型[J]. 化工学报, 2006, 57(4): 719-725. WU Jintao, CHEN Jizhong, YANG Yongrong. Model of contact heat transfer in granular moving bed[J]. Journal of Chemical Industry and Engineering(China), 2006, 57(4): 719-725. |
| [4] |
黄文迪, 许国良. 气固流化床颗粒间辐射换热模型[J]. 华中科技大学学报(自然科学版), 1996(1): 12-16. HUANG Wendi, XU Guoliang. Radiative heat transfer between particles in gas-solid fluidized beds[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition), 1996(1): 12-16. |
| [5] |
孙亮, 孙清, 接鑫, 等. 稻壳热压成型工艺参数试验[J]. 农业机械学报, 2010, 41(1): 96-100. SUN Liang, SUN Qing, JIE Xin, et al. Main technological parameters of rice hull hot briquetting[J]. Transactions of the Chinese Society of Agricultural Machinery, 2010, 41(1): 96-100. |
| [6] |
刘超. 基于ANSYS的生物质成型流变规律及进料螺杆模态特性研究[D]. 济南: 山东大学, 2010. LIU Chao. Study on the rheological rule of biomass briquetting and the modal characteristics of the free screw based on ANSYS[D]. Jinan: Shandong University, 2010. |
| [7] |
邢献军, 李涛, 马培勇, 等. 生物质固体成型燃料热压成型实验研究[J]. 太阳能学报, 2016, 37(10): 2660-2667. XING Xianjun, LI Tao, MA Peiyong, et al. Experimental study of hot molding of densified biofuel[J]. Acta Energiae Solaris Sinica, 2016, 37(10): 2660-2667. DOI:10.3969/j.issn.0254-0096.2016.10.031 |
| [8] |
胡国明. 颗粒系统的离散元素法分析仿真[M]. 武汉: 武汉理工大学出版社, 2010. HU Guoming. Analysis andsimulation of granular system by discrete element method using EDEM[M]. Wuhan: Wuhan University of Technology Press, 2010. |
| [9] |
孙月铢. 基于离散元方法的玉米秸秆粉料压缩成型机理研究[D]. 沈阳: 沈阳农业大学, 2016. SUN Yuezhu. Research on briquettingmechanism of extruding corn stalk power based on discrete element method[D]. Shenyang: Shenyang Agricultural University, 2016. |
| [10] |
WALTON O R, BRAUN R L. Stress calculations for assemblies of inelastic speres in uniform shear[J]. Acta Mechanica, 1986, 63(1-4): 73-86. DOI:10.1007/BF01182541 |
| [11] |
PAN W, HOU X, DING T, et al. Tangential force model study of lunar dust particles based on Hertz-Mindlin theory and sensor technology[J]. Sensor Letters, 2015, 13(2): 176-179(4). DOI:10.1166/sl.2015.3463 |
| [12] |
雷先明, 肖友刚. 物料与窑壁间歇接触对回转窑传热过程的强化效应[J]. 中国工程科学, 2006, 8(8): 39-44. LEI Xianming, XIAO Yougang. Enhancement effect towards heat transfer of rotary kiln by intermittent contact between material and kiln wall[J]. Engineering Sciences, 2006, 8(8): 39-44. |
| [13] |
VARGAS W L, MCCARTHY J J. Unsteady heat conduction in granular materials[J]. Mrs Online Proceedings Library Archive, 2000, 627(5): 1052-1059. |
| [14] |
陈争光, 王德福, 李利桥, 等. 玉米秸秆皮拉伸和剪切特性试验[J]. 农业工程学报, 2012, 28(21): 59-65. CHEN Zhengguang, WANG Defu, LI Liqiao, et al. Experiment on tensile and shearing characteristics of rind of corn stalk[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(21): 59-65. |
| [15] |
WONGSIRIAMNUAY T, TIPPAYAWONG N. Effect of densification parameters on the properties of maize residue pellets[J]. Biosystems Engineering, 2015, 139: 111-120. DOI:10.1016/j.biosystemseng.2015.08.009 |
| [16] |
俞国胜, 侯孟. 生物质成型燃料加工装备发展现状及趋势[J]. 林业机械与木工设备, 2009, 37(2): 4-8. YU Guosheng, HOU Meng. Development status and trend of biomass briquettes processing equipment[J]. Forestry Machinery & Woodworking Equipment, 2009, 37(2): 4-8. |
| [17] |
徐德良, 王思群, 孙军, 等. 木材有效导热系数研究进展[J]. 世界林业研究, 2014, 27(2): 39-44. XU Deliang, WANG Siqun, SUN Jun, et al. Research progress of effective thermal conductivity coefficient of wood[J]. World Forestry Research, 2014, 27(2): 39-44. |
 2018, Vol. 50
2018, Vol. 50



