据统计,因交变载荷造成的疲劳断裂事故占到机械结构失效总数的95%[1].为避免疲劳裂纹可能产生的突然失效, 需要对机械结构进行复杂的检查、探伤、维修[2-3].随着传感器技术的不断发展,在机械系统的设计上越来越多的传感器被安装来采集关键结构的疲劳信息[4-6],支持更为科学的视情维修[7].由于视情维修计划的制定需要参照待维修结构的预期失效时间,因此结构的剩余寿命(remaining useful life,RUL)预测对于基于视情维修的计划制定十分重要.
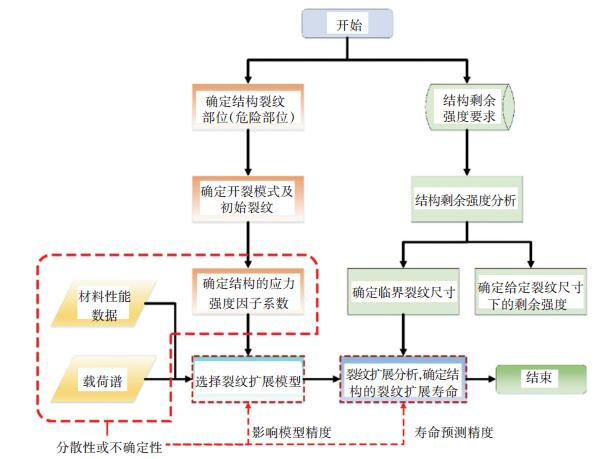
疲劳结构寿命的预测建立在对裂纹扩展寿命的估计基础上.传统的方法是采用损伤容限来获得疲劳结构的裂纹扩展寿命[8].结构损伤容限分析的流程如图 1所示.由于材料的微观结构变化能够对结构的疲劳性能造成很大的影响,而且材料的微观结构很难在制造过程中得到控制,即使采用相同的材料制造相同的结构,制造出的构件也会表现出不同的疲劳性能.为了避免上述这些不确定因素对结构安全带来影响,损伤容限分析通过将裂纹从初始可检尺寸到临界尺寸的扩展寿命除以一个安全系数作为结构的RUL,但这样会造成结构RUL的浪费.因此,利用滤波算法[9]结合结构的实时状态数据(裂纹长度数据)对疲劳性能参数以及裂纹扩展趋势进行估计,能够克服结构状态信息不完备、工况噪声等不确定因素对结构疲劳寿命预测的影响.
|
图 1 结构损伤容限分析流程图 Figure 1 The analysis process of structure damage tolerance method |
疲劳裂纹扩展表现出的非线性特性,决定了针对结构疲劳性能参数的估计是一个非线性滤波问题.非线性卡尔曼滤波算法主要包括:扩展卡尔曼滤波算法(extended Kalman filter,EKF)和无迹卡尔曼滤波算法(unscented Kalman filter,UKF).由于EKF算法截断了非线性模型的线性高阶项,当模型的非线性特性十分显著时,忽略的线性化误差可能导致EKF算法滤波性能下降.为了克服EKF算法存在的缺陷,学者们提出了UKF算法.与EKF算法的线性近似思想不同,UKF通过对非线性模型的概率密度函数的近似来实现对非线性模型的逼近.基于无迹变换,UKF算法利用一组采样得到的Sigma点实现对系统状态参数分布的近似,在状态参数分布服从高斯分布的前提下逼近其均值及方差,再根据传统线性卡尔曼滤波实现递推估计. UKF算法在状态参数估计和设备寿命预测中得到了广泛的运用.胡宇等[10]提出了一种基于改进平方根UKF的方法,并运用于涡扇发动机气路状态的估计;阙子俊等[11]利用UKF算法对轴承性能进行评估,并提出了一种基于UKF的轴承RUL预测方法;Vandyke MC等[12]应用UKF算法对航天飞船的高度状态参数进行估计,并与EKF算法进行了比较,比较结果表明UKF算法优于EKF算法.
本文针对结构疲劳性能参数的分散性问题,基于Paris疲劳裂纹扩展公式建立了适用于UKF的状态参数评估模型,并应用UKF算法对疲劳性能参数和裂纹的扩展趋势进行了估计.最后依据估计的裂纹扩展趋势,对疲劳结构的RUL进行预测.
1 基于Paris疲劳裂纹扩展公式的状态空间评估模型通过对不同种类的结构进行疲劳试验,Molent L等[13]得出了Paris疲劳裂纹扩展公式能够充分处理典型结构的疲劳裂纹扩展问题.因此,本文选取Paris疲劳裂纹扩展公式来建立适应于UKF算法的疲劳性能状态参数评估模型.传统的Paris公式如下:
| $ \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = C{\left( {\Delta K} \right)^m}. $ | (1) |
式中:a表示裂纹长度;N表示应力循环次数;da/dN表示裂纹扩展速率;C和m是材料系数,即疲劳性能参数;ΔK表示应力强度因子幅[14],其与结构裂纹处应力幅值Δσ,裂纹长度a存在如下关系:
| $ \Delta K = \beta \left( a \right)\Delta \sigma \sqrt {\pi a} . $ |
式中:β(a)为裂纹的构型因子(形状系数),与结构细节以及裂纹长度相关.
由式(1)可知,裂纹的扩展是一个连续的累积过程.随着测试技术和传感器技术(如无损检测和智能涂层)的发展,结构在单位循环周期结束的裂纹长度可以通过传感器得到,因此裂纹的扩展可以转化为一个离散的累积过程.通过Euler方法,取dN=1,式(1)转换为如下的离散递归形式:
| $ {a_k} = {a_{k-1}} + C{\left( {\beta \left( {{a_{k-1}}} \right)\Delta \sigma \sqrt {\pi {a_{k-1}}} } \right)^m} = g\left( {{a_{k - 1}}} \right). $ | (2) |
式中:k表示循环周期.由于设备在运行过程中,受到各种工况因素的影响,结构裂纹难免受到噪声污染,因此结构裂纹的扩展过程可以进一步表示如下:
| $ {a_k} = g\left( {{a_{k-1}}} \right) + {w_{a, k-1}}. $ | (3) |
式中:wa, k-1为系统过程噪声,且其服从wa, k-1~N(0, Qa, k).
裂纹长度是通过传感器测量得到的,由于测量环境和传感器自身误差等因素,测量过程中难免引入误差,裂纹长度测量模型表示如下:
| $ {z_k} = h\left( {{a_k}} \right) + {v_k}. $ | (4) |
式中:h表示测量函数,在本文中为恒等函数;vk表示裂纹长度测量误差,且其服从vk~N(0, Rk).
由式(2)可知,疲劳性能参数C和m的分散性,会造成裂纹长度呈现出一定的分散性.因此本文将裂纹长度a作为另一个需要评估的状态参数,则待评估的状态参数向量表示为X=[a C m]T.式(3)进一步的转换为
| $ {\mathit{\boldsymbol{X}}_k} = \left[\begin{array}{l} {a_k}\\ {C_k}\\ {m_k} \end{array} \right] = \left[\begin{array}{l} g\left( {{a_{k-1}}} \right)\\ {C_{k-1}}\\ {m_{k-1}} \end{array} \right] + \left[\begin{array}{l} {w_{a, k-1}}\\ {w_{C, k-1}}\\ {w_{m, k-1}} \end{array} \right] = \mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{X}}_{k -1}}} \right) + {\mathit{\boldsymbol{W}}_{k -1}}. $ | (5) |
式中:wC, k-1~N(0, QC, k-1)和wm, k-1~N(0, Qm, k-1)分别为C和m的高斯白噪声;QC, k-1和Qm, k-1分别由材料的疲劳试验确定,在本文的3.1节中详细介绍.系统过程噪声以矩阵的形式表示为:
| $ {\mathit{\boldsymbol{Q}}'_k} = {\rm{diag}}\left( {{Q_{a, k-1}}, {Q_{C, k-1}}, {Q_{m, k-1}}} \right). $ |
由式(5)可知,疲劳性能参数C和m对裂纹扩展增量有很大的影响,因此本文选取从第k-1到第k步的裂纹扩展增量作为附加的测量变量.由式(4),系统的观测方程进一步的表示如下:
| $ {\mathit{\boldsymbol{Z}}_k} = \left[\begin{array}{l} {z_{a, k}}\\ {a_{grow\_a, k}} \end{array} \right] = \left[\begin{array}{l} {a_k}\\ {a_k}-{a_{k-1}} \end{array} \right] + \left[\begin{array}{l} {v_k}\\ 0 \end{array} \right] = \mathit{\boldsymbol{h'}}\left( {{x_k}} \right) + {\mathit{\boldsymbol{R}}_k}. $ | (6) |
由于裂纹的增量计算误差可以被裂纹长度测量误差所包含,因此本文取裂纹增量计算误差为0.系统的测量误差以矩阵的形式表示为
| $ {R_k} = {\rm{diag}}\left( {{R_{k-1}}, 0} \right). $ |
式(5)和式(6)分别为系统的状态转移方程和观测方程.由于方程中状态参数a,C和m存在分散性,因此需要对其进行评估(滤波).
2 基于UKF的状态参数评估和剩余寿命预测 2.1 基于UKF的状态参数评估基于逼近非线性系统模型的概率密度函数比获得非线性系统的解析模型要简单的思想,通过无迹变换,UKF算法利用一组确定性采样的Sigma点来逼近系统状态参数分布,即将Sigma点带入非线性模型中,得到对应的非线性模型数值点集,通过得到的点集求得变换后的均值和方差.假设n维状态向量X的均值和方差分别为X和P,根据无迹变换,在x的周围可以构造一组Sigma点{χ0, χ2, ..., χ2n}和对应的权重{ω0, ω2, ..., ω2n}如下:
| $ {\mathit{\boldsymbol{\chi }}_i} = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar X}}, \;\;\;\;\;i = 0;}\\ {\mathit{\boldsymbol{\bar X}} + {{\left( {\sqrt {\left( {n + \kappa } \right)\mathit{\boldsymbol{P}}} } \right)}_i}, \;\;\;\;i = 1, ..., n;}\\ {\mathit{\boldsymbol{\bar X}}-{{\left( {\sqrt {\left( {n + \kappa } \right)\mathit{\boldsymbol{P}}} } \right)}_i}, i = n + 1, ..., 2n.} \end{array}} \right. $ | (7) |
| $ {\omega _i} = \left\{ {\begin{array}{*{20}{c}} {\omega _0^m = \lambda /\left( {n + \lambda } \right);}\\ {\omega _0^c = \lambda /\left( {n + \lambda } \right) + \left( {1- {\alpha ^2} + \beta } \right);}\\ {\omega _i^m = \omega _i^c = 1/\left[{2\left( {n + \lambda } \right)} \right], \;\;\;i = 1, ..., 2n.} \end{array}} \right. $ | (8) |
式中:λ=α2(n+κ)-n;ωim和ωic分别表示Sigma点χi的均值权重和方差权重;参数α确定了X周围Sigma点集的分布,用于调节采样得到的Sigma点和x的距离,且0≤α≤1;参数β包含了先验分布的高阶矩信息,对于正态分布β=2为最优值;参数κ为第二尺度参数,用于保证(n+κ)Px为半正定矩阵,当n≥3时κ=0,当n < 3时κ=n-3.
利用UKF算法对疲劳性能状态参数的估计过程表示如下:
Step 1 初始化:k=0.
对需要进行估计的状态参数进行初始化,设置状态参数均值和方差分别为X0=[a0, C0, m0]T和P0;
for k=1, 2, …, do
Step 2 计算Sigma点集和对应的权重:
根据式(7)和式(8)产生Sigma点集{χ0, k-1, χ2, k-1, ..., χ6, k-1}及对应的权重{ω0, k-1, ω2, k-1, ..., ω6, k-1};
Step 3 时间预测:
1) 利用非线性系统状态方程传递Sigma点:
根据式(5),可得χ′i, k-1=f(χi, k-1)(i=0, ..., 6).
2) 状态参数的预测:
| $ {\mathit{\boldsymbol{X}}_{k|k-1}} = \sum\limits_{i = 0}^6 {{\omega _{i, k-1}}{{\mathit{\boldsymbol{\chi '}}}_{i, k-1}}} . $ |
3) 状态参数方差矩阵计算:
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{x, k|k-1}} = \sum\limits_{i = 0}^6 {{\omega _{i, k-1}}\left( {{{\mathit{\boldsymbol{\chi '}}}_{i, k-1}} - {\mathit{\boldsymbol{X}}_{k|k - 1}}} \right)\left( {{{\mathit{\boldsymbol{\chi '}}}_{i, k - 1}} - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left. {{\mathit{\boldsymbol{X}}_{k|k - 1}}} \right)^{\rm{T}}} + {{\mathit{\boldsymbol{Q'}}}_k}. \end{array} $ |
4) sigma采样点观测值计算:
| $ {\mathit{\boldsymbol{\gamma }}_{i, k-1}} = \mathit{\boldsymbol{h}}\left( {{{\mathit{\boldsymbol{\chi '}}}_{i, k-1}}} \right)\left( {i = 0, ..., 6} \right). $ |
5) 测量值预测:
| $ {\mathit{\boldsymbol{z}}_{k|k-1}} = \sum\limits_{i = 0}^6 {{\omega _{i, k-1}}{\mathit{\boldsymbol{\gamma }}_{i, k-1}}.} $ |
6) 测量值方差计算:
| $ {\mathit{\boldsymbol{P}}_{z, k}} = \sum\limits_{i = 0}^6 {{\omega _{i, k-1}}\left( {{\mathit{\boldsymbol{\gamma }}_{i, k-1}}-{z_{k|k - 1}}} \right){{\left( {{\mathit{\boldsymbol{\gamma }}_{i, k - 1}} - {\mathit{\boldsymbol{z}}_{k|k - 1}}} \right)}^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k}} . $ |
Step 4 测量更新:
1) 系统状态参数与测量值的协方差计算:
| $ {\mathit{\boldsymbol{P}}_{xz, k}} = \sum\limits_{i = 0}^6 {{\omega _{i, k-1}}\left( {{{\mathit{\boldsymbol{\chi '}}}_{i, k-1}}-{\mathit{\boldsymbol{X}}_{k|k - 1}}} \right){{\left( {{{\mathit{\boldsymbol{\chi '}}}_{i, k - 1}} - {\mathit{\boldsymbol{z}}_{k|k - 1}}} \right)}^{\rm{T}}}.} $ |
2) 卡尔曼增益矩阵计算:
| $ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{xz, k}}\mathit{\boldsymbol{P}}_{z, k}^{-1}. $ |
状态参数均值和方差更新:
| $ {\mathit{\boldsymbol{X}}_k} = {\mathit{\boldsymbol{X}}_{k|k-1}} + \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{z}}_k}-{\mathit{\boldsymbol{z}}_{k|k-1}}} \right), $ |
其中zk为在第k步对应时刻由传感器获得的状态参数信息.
| $ {\mathit{\boldsymbol{P}}_{x, k}} = {\mathit{\boldsymbol{P}}_{x, k|k-1}}-{\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{P}}_{z, k}}{\mathit{\boldsymbol{K}}_k}^{\rm{T}}. $ |
end for
2.2 基于UKF的剩余寿命预测由上可知,通过利用UKF算法更新疲劳性能参数状态方程至第k步,可以得到第k步对应时刻的疲劳性能参数的评估值Xk=[ak, Ck, mk]T.根据式(3)建立的疲劳裂纹扩展离散递归模型,可以得到k+l(l>0)时刻的疲劳裂纹长度ak+l:
| $ \begin{array}{l} {a_{k + 1}} = {a_k} + {C_k}\left( {^\beta \left( {{a_k}} \right)} \right){m_k};\\ {a_{k + 2}} = {a_{k + 1}} + {C_k}\left( {^\beta \left( {{a_{k + 1}}} \right)} \right){m_k};\\ \;\;\;\;\;\;\;\; \vdots \\ {a_{k + l}} = {a_{k + l-1}} + {C_k}\left( {^\beta \left( {{a_{k + l-1}}} \right)} \right){m_k}. \end{array} $ | (9) |
满足式(9)的最小l定义为k时刻预测的疲劳裂纹RUL:
| $ {a_{k + l}} \ge {a_c}. $ |
式中,ac表示通过飞机结构疲劳试验得到的结构临界疲劳裂纹长度.
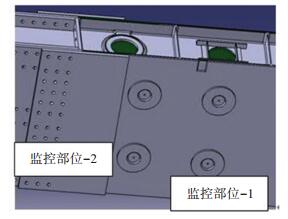
3 案例分析 3.1 飞机结构疲劳试验本文在相同的试验环境下对5个相同的壁板试件进行了疲劳试验.如图 2所示为试验所采用的壁板,壁板的两个位置装有疲劳裂纹监测传感器.
|
图 2 机身壁板 Figure 2 The fuselage panel |
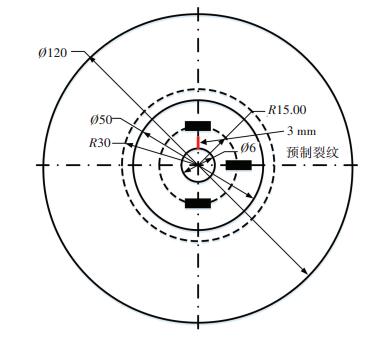
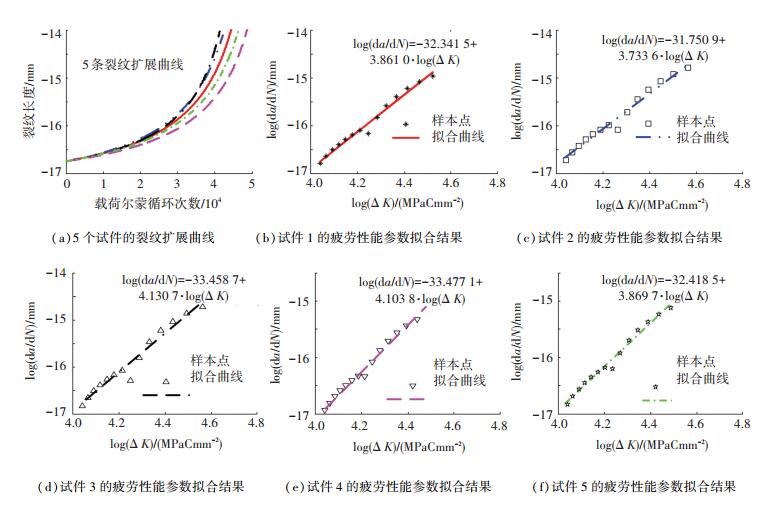
试件的材料为在2024-T351铝合金.试验设备为Inston8801电液伺服疲劳试验机.试验采用试验机配置的da/dN软件记录裂纹长度及载荷循环次数.试验采用正弦波对试件进行加载,载荷频率为290 kHz,最大载荷为4.5 kN,应力比为0.2.如图 3所示,为了控制裂纹的扩展方向,在紧固孔的一侧预制了一个3 mm的初始裂纹.如图 4(a)所示为5个试件的疲劳裂纹扩展曲线.
|
图 3 预制裂纹 Figure 3 A 3mm notch |
|
图 4 5个试样的裂纹扩展曲线及其疲劳性能参数拟合结果 Figure 4 The experimental fatigue crack growth curves of the 5 specimens and the crack growth rate versus stress intensity factor range of the 5 specimens |
对式(1)两边取对数,得到
| $ \log \frac{{{\rm{d}}a}}{{{\rm{d}}N}} = \log C + m*\log \Delta K. $ | (10) |
显然,log(da/dN)和logΔK之间呈线性关系.通过将试验所得的5个试样的a~N曲线采用7点递增多项式法进行数据处理,并将得到的数据运用最小二乘法进行线性拟合,可求得式(10)中的疲劳性能参数C和m. 图 4(b)~(f)分别为5个试样的疲劳性能参数拟合结果,具体的C和m值如表 1所示.
| 表 1 5个试样的疲劳性能参数C和m Table 1 The fatigue performance parameters, C and m, of the 5 specimens |
由表 2可知,在相同的试验条件下,5个试件的2个疲劳性能参数表现出不同程度的分散性.现有的大量试验数据统计研究发现[15],logC和m服从正态分布,为UKF算法的应用提供了条件.通过对5个试件的数据进行统计分析,可以得到logC~N(-32.68, 0.672)和m~N(3.94, 0.142).
| 表 2 仿真实验参数设置 Table 2 Parameters for numerical study |
用于UKF算法仿真实验的参数设置如表 2所示.依据3.2节中对疲劳性能参数数据的统计分析,本文分别选取3个状态参数的分布均值作为其初始状态.
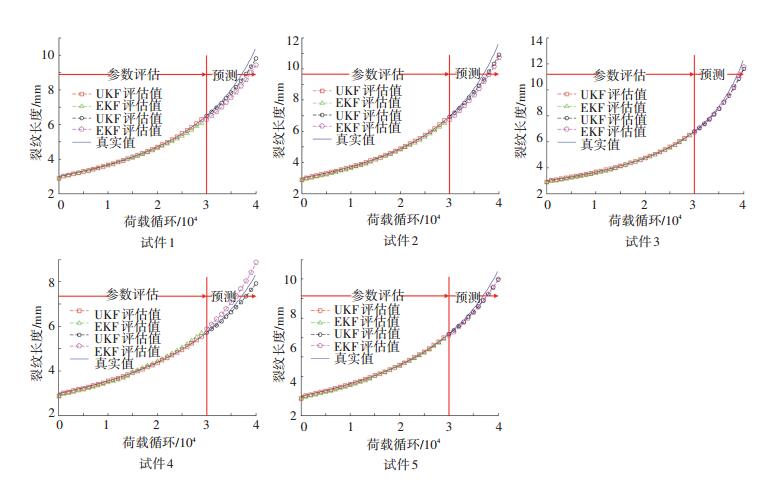
基于表 2的实验参数设置,本文选取5个试件的前30 000个载荷循环的疲劳裂纹数据,利用UKF算法对疲劳性能状态参数进行估计,根据估计得到的状态参数结果并对未来的10 000个载荷循环下的结构裂纹长度进行预测.为了更好地分析UKF算法在处理本文问题上的收敛性,使得到的仿真结果更可信,本文针对5个试样分别进行了30次仿真,并选取EKF算法进行了对比实验分析.如图 5所示,为5个试件的仿真结果.
|
图 5 5个试件的仿真结果 Figure 5 The experimental results of the 5 specimens |
本文分别利用30次仿真的均值及其与真实值的绝对相对误差来评估UKF算法的收敛性.均值和绝对相对误差的计算如下:
| $ {\bar a_k} = \frac{1}{{30}}\sum\limits_{i = 1}^{30} {{{\hat a}_{k, i}}}, $ |
| $ {E_k} = \frac{{\left| {{{\bar a}_k}-{a_k}} \right|}}{{{a_k}}} \times 100\% . $ |
式中:
为了分析30次仿真实验结果的分散性,分别计算了30次仿真的结果与真实值的方差,以及30次仿真的结果与其均值的方差,计算公式如下:
| $ \begin{array}{l} {V_k} = \frac{1}{{29}}\sum\limits_{i = 1}^{30} {{{\left( {{{\hat a}_{k, i}}-{a_k}} \right)}^2}}, \\ {{\bar V}_k} = \frac{1}{{29}}\sum\limits_{i = 1}^{30} {{{\left( {{{\hat a}_{k, i}}-{{\bar a}_k}} \right)}^2}} . \end{array} $ |
式中:Vk为30次仿真的结果与真实值的方差,Vk为30次仿真的结果与其均值的方差.
本文分别选取试件1和2在不同载荷循环下(k=5 000,10 000,15 000,20 000,25 000,30 000,32 000,34 000,36 000,38 000,40 000)得到的4个评估参数(ak,Ek,Vk和Vk)来分析UKF和EKF算法在结构疲劳裂纹预测问题上的表现.试件1和2的4个评估参数计算结果如表 3所示.
| 表 3 试件1和2的4个评估参数计算结果 Table 3 The result of four evaluation parameters for specimens 1 and 2 |
根据ak和Ek反映了算法在处理本文问题上的收敛性,由表 3可知,UKF和EKF算法在参数评估阶段都表现出了很好的收敛性,在预测阶段2个算法的收敛性都有所下降,但绝对相对误差都小于10%,且UKF算法在收敛性上整体都优于EKF算法.根据Vk反映了30次仿真的实验值与真实值的距离,由表 3可知,UKF算法在参数评估和预测阶段的分散性都十分小,且UKF算法在分散性的表现上整体都优于EKF算法.根据Vk反映了30次仿真的实验值与其均值的距离,由表 3可知,UKF算法在参数评估和预测阶段的分散性都十分小,而EKF算法在预测阶段分散性显著增大.由以上分析可知,UKF算法可以较为准确地预测出结构疲劳裂纹的真实尺寸.基于以上的分析结果,本文利用UKF和EKF算法对5个试件的剩余寿命进行了30次仿真预测,结果如表 4所示.
| 表 4 5个试件的剩余寿命预测结果 Table 4 The RUL prediction result of the 5 specimens |
由表 4可知,UKF算法在试件1,2,3和5上的预测结果都要优于EKF算法,且预测得到的RUL绝对相对误差都小于10%.由此可见UKF算法能够很好地处理结构疲劳裂纹剩余寿命预测问题.
4 结论1) 本文提出的结合UKF的结构疲劳裂纹RUL预测方法,能够避免EKF算法在处理非线性特性十分显著模型时性能下降的弊端.
2) 基于Paris疲劳裂纹扩展公式,建立了适用于UKF算法的疲劳性能状态参数评估模型,克服了传统Paris疲劳裂纹扩展模型无法处理结构状态信息不完备、工况噪声等不确定因素的困难.
3) 利用疲劳试验数据,对提出的RUL预测方法进行了仿真分析.仿真结果表明:提出的方法能够很好地处理疲劳裂纹扩展模型中疲劳性能参数的不确定性,且在剩余寿命预测上与EKF算法进行了比较,比较结果表明UKF算法优于EKF算法.
| [1] |
高镇同, 熊峻江. 疲劳可靠性[M]. 北京: 北京航空航天大学出版社, 2000: 1-10. GAO Z T, XIONG J J. Fatigue reliability[M]. Beijing: Beihang University Press, 2000: 1-10. |
| [2] |
刘芳, 赵建印, 宋贵宝. 任务准备阶段机群战备完好率评估模型[J]. 哈尔滨工业大学学报, 2008, 40(3): 488-491. LIU F, ZHAO J Y, SONG G B. Model on evaluating operational readiness of an air fleet during mission ready time[J]. Journal of Harbin Institute of Technology, 2008, 40(3): 488-491. DOI:10.3321/j.issn:0367-6234.2008.03.035.j.issn:0367-6234.2008.03.035 |
| [3] |
LIN L, LUO B, ZHONG S S. Development and application of maintenance decision-making support system for aircraft fleet[J]. Advances in Engineering Software, 2017, 114: 192-207. DOI:10.1016/j.advengsoft.2017.07.001 |
| [4] |
白生宝, 肖迎春, 刘马宝, 等. 智能涂层传感器监测裂纹的工程适用性[J]. 无损检测, 2015, 37(1): 42-44. BAI S B, XIAO Y C, LIU M B, et al. Engineering applicability of monitoring crack by smart coatings sensor[J]. Nondestructive Testing, 2015, 37(1): 42-44. |
| [5] |
PARK C, PETERS K. Optimization of embedded sensor placement for structural health monitoring of composite airframes[J]. AIAA Journal, 2012, 50(11): 2536-2545. DOI:10.1016/j.engstruct.2017.08.070 |
| [6] |
STASZEWSKI W J. Fatigue crack detection using smart sensor technologies[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010, 31(8): 609-610. DOI:10.1016/j.procir.2016.11.260 |
| [7] |
周炳海, 陶红玉, 綦法群. 带随机突变的两阶段退化系统视情维修建模[J]. 哈尔滨工业大学学报, 2016, 48(1): 87-93. ZHOU B H, TAO H Y, QI F Q. Condition-based maintenance modeling for two-stage deteriorating systems with random change[J]. Journal of Harbin Institute of Technology, 2016, 48(1): 87-93. DOI:10.11918/j.issn.0367-6234.2016.01.013 |
| [8] |
陈勃, 鲍蕊, 张建宇, 等. 飞机结构耐久性/损伤容限综合设计与分析[J]. 北京航空航天大学学报, 2004, 30(2): 139-142. CHEN B, BAO R, ZHANG J Y, et al. Combined analysis model on aircraft structural durability and damage tolerance[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(2): 139-142. DOI:10.3969/j.issn.1001-5965.2004.02.011 |
| [9] |
WANG H K, HAYNES R, HUANG H Z, et al. The use of high-performance fatigue mechanics and the extended Kalman/particle filters for diagnostics and prognostics of aircraft structures[J]. Cmes Computer Modeling in Engineering & Sciences, 2015, 105(1): 1-24. DOI:10.1201/b18009-2 |
| [10] |
胡宇, 杨月诚, 张世英, 等. 基于改进平方根无迹卡尔曼滤波方法的涡扇发动机气路状态监控[J]. 航空动力学报, 2014, 29(2): 441-450. HU Y, YANG Y C, ZHANG S Y, et al. Turbofan engine gas path performance monitoring based on improved square root unscented Kalman filter[J]. Journal of Aerospace Power, 2014, 29(2): 441-450. DOI:10.1322/j.cnki.jasp.2014.02.025 |
| [11] |
阙子俊, 金晓航, 孙毅. 基于UKF的轴承剩余寿命预测方法研究[J]. 仪器仪表学报, 2016, 37(9): 2036-2043. QUE Z J, JIN X H, SUN Y. Remaining useful life prediction for bearings with the unscented Kalman filter-based approach[J]. Chinese Journal of Scientific Instrument, 2016, 37(9): 2036-2043. DOI:10.3969/j.issn.0254-3087.2016.09.015 |
| [12] |
VANDYKE M C, SCHWARTZ J L, HALL C D. Unscented Kalman filtering for spacecraft attitude state and parameter estimation[C]//AAS/AIAA Space Flight Mechanics Conference. Providence: AAS/AIAA, 2004.
|
| [13] |
MOLENT L, BARTER S A. A comparison of crack growth behaviour in several full-scale airframe fatigue tests[J]. International Journal of Fatigue, 2007, 29(6): 1090-1099. DOI:10.1016/j.ijfatigue.2006.09.015 |
| [14] |
XIONG J J, SHENOI R A. A practical randomization approach of deterministic equation to determine probabilistic fatigue and fracture behaviours based on small experimental data sets[J]. International Journal of Fracture, 2007, 145(4): 273-283. DOI:10.1007/s10704-007-9116-z |
| [15] |
WU W F, NI C C. Probabilistic models of fatigue crack propagation and their experimental verification[J]. Probabilistic Engineering Mechanics, 2004, 19(3): 247-257. DOI:10.1016/j.probengmech.2004.02.008 |
 2018, Vol. 50
2018, Vol. 50


