当前,在机器人领域、航天工程领域、医疗器械领域中,机械系统的设计要求日益提高,以实现更高的定位精度以及良好的动态性能,在设计、制造及调试过程中需要深入考虑的因素越来越多,其设计思想也愈发全面[1-2].由于设计滑动摩擦副的配合需要形成规则的装配间隙[3-4],同时运动副组成构件在加工制造过程中也必然会出现误差,以及长期工作过程中,运动副接触表面磨损引起的材料损失将造成规律各异的附加间隙.因此,在几乎所有机器的运动副中,都无法避免连接组件之间存在一定间隙[5-6],而间隙的存在对机构动力学特性影响是非常显著的.因此,运动副中不论存在何种间隙对机构整体的影响都是不利的.
在含间隙机构的动力学研究中,对机构进行准确且可解的动力学建模至关重要,诸多学者对此做出了大量的工作.当前,含间隙关节副动力学建模主要基于三种方法:无质量杆间隙模型,两状态非连续接触模型以及多状态非连续接触模型[7-9].基于以上含间隙关节的建模方法,众多国内外学者展开了含间隙机构的动力学性能研究. Paulo Flores[10]等针对含多个间隙关节的平面四杆机构展开研究,详细分析了驱动速度、间隙尺寸对其动力学性能的影响,结果表明驱动转速的增加以及间隙尺寸的增大都会降低机构的动力学性能. Onesmus Muvengei[11]等人研究了间隙关节副位置的不同和间隙尺寸差异对机构运行稳定性的影响,并通过运动相图和庞加莱图分析了不同位置关节副间隙的尺寸变化对整体系统周期性行为敏感程度的差异.赵刚练[12]等人建立了含间隙的圆柱副的模型,并将该模型应用到多刚体动力学计算,以简单二自由度机构为例进行动力学仿真,验证了模型的正确性.目前含关节间隙机构动力学建模多限于平面机构,关节间隙对空间机构机构运动特性影响的研究文献较少.
空间RSSR机构的运动特性比平面四杆机构复杂,结构紧凑,运动多样,灵活可靠,可以实现复杂的空间运动的传递,在工程上有许多特殊的用途, 在各种工作机械、发动机以及仪表机构中得到大量的应用.本文对含球关节间隙的RSSR机构进行运动学分析与动力学建模,并通过编程对其动力学特性进行仿真研究, 分析不同接触力碰撞模型下,间隙量、输入转速等关键参数对RSSR机构动态性能的影响.
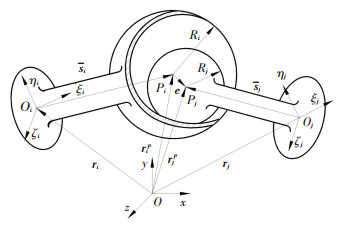
1 含间隙球关节运动学模型的建立如图 1所示,该图描述了含间隙的球关节副元素处于分离状态时的运动状态.其中下脚标i代表第i号构件,下脚标j代表第j号构件.现将图中各标注含义说明如下:
|
图 1 含间隙球关节示意 Figure 1 General view of the spherical joint with clearance |
x、y、z为全局坐标系;ξi, ηi, ζi为建立在第i号构件Oi点处的局部坐标系;ξj, ηj, ζj为建立在第j号构件Oj点处的局部坐标系;Ri, Rj为球窝与球头的半径大小;si, sj为球窝与球头中心点Pi, Pj分别为在其局部坐标系中的位置矢量;riP, rjP为全局坐标系中,球窝与球头中心点的位置向量;ri, rj为全局坐标系中,点Oi,Oj的位置向量,e为连接球窝与球头中心点的矢量,被定义为偏心矢量,该矢量随关节副元素之间相互运动其大小、方向将产生变化.
为方便说明与理解,此处将关节间隙量放大.在实际机械系统中,关节间隙量远小于球头与球窝半径.
球窝与球头中心点的偏心矢量e可表示为
| $ \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{r}}_j^p - \mathit{\boldsymbol{r}}_i^p. $ | (1) |
式(1)中,rip, rjp可表示为
| $ \mathit{\boldsymbol{r}}_k^p = {\mathit{\boldsymbol{r}}_k} + {\mathit{\boldsymbol{A}}_k}{{\mathit{\boldsymbol{\bar s}}}_k}.\left( {k = i,j} \right) $ | (2) |
式(2)中,Ak代表局部坐标系对全局坐标系的方向矩阵.而偏心量e的模e可写做
| $ e = \sqrt {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{e}}} . $ |
上式可以进一步写为
| $ e = \sqrt {{{\left( {x_j^p - x_i^p} \right)}^2} + {{\left( {y_j^p - y_i^p} \right)}^2} + {{\left( {z_j^p - z_i^p} \right)}^2}} . $ |
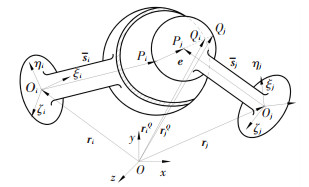
图 2描述了处于接触状态的含间隙球关节.当球头接触碰撞球窝时,运动副材料可视为弹性体,会产生接触嵌入,球窝和球头上的接触点分别为Qi和Qj.接触点法向方向的单位向量可以写做
| $ \mathit{\boldsymbol{n}} = \frac{\mathit{\boldsymbol{e}}}{e}. $ | (3) |
|
图 2 球头与球窝接触嵌入 Figure 2 Penetration depth between the socket and the ball |
球窝与球头的接触点在全局坐标系下的向量描述可由下式给出:
| $ \mathit{\boldsymbol{r}}_k^Q = {\mathit{\boldsymbol{r}}_k} + {\mathit{\boldsymbol{A}}_k}{{\mathit{\boldsymbol{\bar s}}}_k} + {R_k}\mathit{\boldsymbol{n}}.\left( {k = i,j} \right) $ | (4) |
球头与球窝接触点的矢量差可表示为
| $ \mathit{\boldsymbol{\delta }} = \mathit{\boldsymbol{r}}_j^Q - \mathit{\boldsymbol{r}}_i^Q. $ |
同时为便于后续计算,δ的模长δ表示嵌入深度,也可以用式(5)表示:
| $ \delta = e - c. $ | (5) |
式中,c=Ri-Rj为关节间隙量.碰撞过程中接触点Qi和Qj在全局坐标系中的速度可由式(4)对时间求一阶导数给出:
| $ \mathit{\boldsymbol{\dot r}}_k^Q = {{\mathit{\boldsymbol{\dot r}}}_k} + {{\mathit{\boldsymbol{\dot A}}}_k}{{\mathit{\boldsymbol{\bar s}}}_k} + {R_k}\mathit{\boldsymbol{\dot n}}.\left( {k = i,j} \right) $ | (6) |
式(6)中矢量
接触点的法向相对速度以及切向相对速度分别由VN和VT表示.法向相对速度反应了运动副副元素之间的接触、碰撞和分离,切向速度反应了运动副副元素之间的相对滑移运动.接触面法向和切向的相对速度矢量可由碰撞点之间的相对速度向法向和切向方向投影得到
| $ {\mathit{\boldsymbol{V}}_{\rm{N}}} = \left[ {{{\left( {\mathit{\boldsymbol{\dot r}}_j^Q - \mathit{\boldsymbol{\dot r}}_i^Q} \right)}^{\rm{T}}}\mathit{\boldsymbol{n}}} \right]\mathit{\boldsymbol{n}}, $ |
| $ {\mathit{\boldsymbol{V}}_{\rm{T}}} = {\left( {\mathit{\boldsymbol{\dot r}}_j^Q - \mathit{\boldsymbol{\dot r}}_i^Q} \right)^{\rm{T}}} - {\mathit{\boldsymbol{V}}_{\rm{N}}} = {V_{\rm{T}}}\mathit{\boldsymbol{t}}. $ |
式中,t表示接触碰撞面的切线方向,并假定球头与球窝开口处没有接触.碰撞过程中所产生接触力包括法向力和切向力,分别由fN和fT表示.作用在构件i质心点Oi处的等价力和力矩分别为
| $ {\mathit{\boldsymbol{f}}_i} = {\mathit{\boldsymbol{f}}_{\rm{T}}} + {\mathit{\boldsymbol{f}}_{\rm{N}}}, $ |
| $ {\mathit{\boldsymbol{M}}_i} = \left( {{\mathit{\boldsymbol{s}}_i} + {R_i}\mathit{\boldsymbol{n}}} \right) \times {\mathit{\boldsymbol{f}}_i}. $ |
式中,si为si在全局坐标系下的表示.作用在构件j质心点Oj处的等价的力和力矩为
| $ {\mathit{\boldsymbol{f}}_j} = - {\mathit{\boldsymbol{f}}_i}, $ |
| $ {\mathit{\boldsymbol{M}}_j} = \left( {{\mathit{\boldsymbol{s}}_j} + {R_j}\mathit{\boldsymbol{n}}} \right) \times {\mathit{\boldsymbol{f}}_j}. $ |
式中,sj为sj在全局坐标系下的表示.关节副元素之间的相互作用力,或者接触力的大小用Fn表示,其有无依赖于参数δ,可以表示为
| $ \left\{ \begin{array}{l} {F_n} = 0,\;\;\;\;\delta \le 0;\\ {F_n} \ne 0,\;\;\;\;\delta > 0. \end{array} \right. $ |
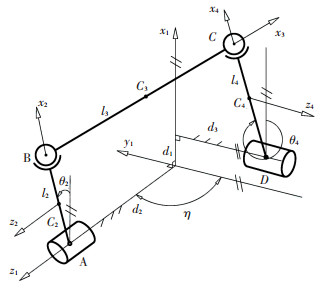
图 3所示为典型的空间单自由度RSSR机构,各构件从基座开始编号依次为1~4,其中为l2曲柄,l4摇杆,l3为连杆.在空间RSSR机构的运动学分析中,连杆处有一绕自身轴向方向旋转的局部自由度,因为其不影响全局运动学规律,因此在分析中忽略连杆处的局部自由度. 图 3中θ2为输入角,θ4为输出角,η为曲柄转轴与摇杆转轴轴线的夹角,此处称扭角,机构几何参数的数值见表 1.
|
图 3 RSSR机构示意图 Figure 3 Sketch of the RSSR mechanism |
| 表 1 RSSR机构几何参数 Table 1 Geometrical parameters of RSSR mechanism |
图 3中RSSR机构各点坐标如下:
| $ \mathit{\boldsymbol{A}} = {\left[ {0,0,{d_2}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{B}} = {\left[ {{l_2}\cos {\theta _2}, - {l_2}\sin {\theta _2},{d_2}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{d_1} + {l_4}\cos {\theta _4}}\\ { - {d_3}\sin \eta + {l_4}\sin {\theta _4}\cos \eta }\\ {{d_3}\cos \eta + {l_4}\sin {\theta _4}\sin \eta } \end{array}} \right], $ |
| $ \mathit{\boldsymbol{D}} = {\left[ {{d_1}, - {d_3}\sin \alpha ,{d_3}\cos \eta } \right]^{\rm{T}}}. $ |
根据封闭矢量法,建立几何关系方程,可求出输入转角θ2与输出转角θ4的关系为
| $ \left| {\mathit{\boldsymbol{C}} - \mathit{\boldsymbol{B}}} \right| = {l_3}, $ |
求解该方程可得
| $ {\theta _4} = \frac{{2\arctan \left( {{p_3} - \sqrt {p_3^2 + p_2^2 - p_1^2} } \right)}}{{{p_1} - {p_2}}}. $ |
式中,p1, p2, p3作为中间变量,表示为
| $ \begin{array}{*{20}{c}} {{p_1} = l_2^2 - l_3^2 + l_4^2 + d_1^2 + d_2^2 + d_3^2 - 2{d_2}{d_3}\cos \eta + }\\ {2{l_2}{d_3}\sin \eta \sin {\theta _2} - 2{l_2}{d_1}\cos {\theta _2},} \end{array} $ |
| $ {p_2} = 2{l_4}{d_1} - 2{l_2}{l_4}\cos {\theta _2}, $ |
| $ {p_3} = - 2{l_4}{d_2}\sin \eta + 2{l_2}{l_4}\sin {\theta _2}\cos \eta . $ |
当RSSR机构关节不含间隙,所受运动约束为完整约束.通过机构中各构件质心位置的坐标(x, y, z)以及表示构件旋转姿态的欧拉角(α, β, γ)来定义机构的广义坐标矢量. 图 3中,C2, C3, C4分别代表各活动构件的质心点,RSSR机构各活动构件广义坐标可以定义为
| $ {\mathit{\boldsymbol{q}}_2} = {\left[ {\begin{array}{*{20}{c}} {{x_2}}&{{y_2}}&{{z_2}}&{{\theta _2}} \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{q}}_3} = {\left[ {\begin{array}{*{20}{c}} {{x_3}}&{{y_3}}&{{z_3}}&\alpha &\beta &\gamma \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{q}}_4} = {\left[ {\begin{array}{*{20}{c}} {{x_4}}&{{y_4}}&{{z_4}}&{{\theta _4}} \end{array}} \right]^{\rm{T}}}. $ |
RSSR机构的系统广义坐标为
| $ \mathit{\boldsymbol{q}} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{q}}_2^{\rm{T}}}&{\mathit{\boldsymbol{q}}_3^{\rm{T}}}&{\mathit{\boldsymbol{q}}_4^{\rm{T}}} \end{array}} \right]^{\rm{T}}}. $ |
运动约束方程组可以写为
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_1}:{x_2} - \frac{1}{2}{l_2}{\rm{c}}{\theta _2} = 0,{y_2} - \frac{1}{2}{l_2}{\rm{s}}{\theta _2} = 0,{z_2} - {d_2} = 0. $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_2}:{x_2} + {l_2}{\rm{c}}{\theta _2} - \left( { - \frac{1}{2}{l_3}{\rm{c}}\gamma {\rm{c}}\beta + {x_3}} \right) = 0,{y_2} + {l_2}{\rm{s}}{\theta _2} - \\ \;\;\;\;\;\;\left( { - \frac{1}{2}{l_3}{\rm{s}}\gamma {\rm{c}}\beta + {y_3}} \right) = 0,{z_2} - \left( {\frac{1}{2}{l_3}{\rm{s}}\beta + {z_3}} \right) = 0. \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_3}:\left( {{x_3} + \frac{1}{2}{l_3}{\rm{c}}\gamma {\rm{c}}\beta } \right) - \left( {{x_4} + \frac{1}{2}{l_4}{\rm{c}}{\theta _4} + {d_1}} \right) = 0,\\ \;\;\;\;\;\;\left( {{y_3} + \frac{1}{2}{l_3}{\rm{s}}\gamma {\rm{c}}\beta } \right) - \left( { - {d_3}} \right) = 0,\\ \;\;\;\;\;\;{z_3} - \frac{1}{2}{l_3}{\rm{s}}\beta - \left( {{z_4} + \frac{1}{2}{l_4}{\rm{s}}{\theta _4}} \right) = 0. \end{array} $ |
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_3}:{x_4} - \frac{1}{2}{l_4}{\rm{c}}{\theta _4} - {d_1} = 0,\\ \;\;\;\;\;{y_4} - \left( { - {d_3}} \right) = 0,\\ \;\;\;\;\;{z_4} - \frac{1}{2}{l_4}{\rm{s}}{\theta _4} = 0. \end{array} $ |
式中:c θi=cos θi, s θi=sin θi.
在理想情况下,不考虑间隙作用,根据拉格朗日乘子法,机构的动力学方程如下式所示:
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ \mathit{\boldsymbol{C}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot q}}}\\ \mathit{\boldsymbol{\lambda }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{F}}\\ \mathit{\boldsymbol{\gamma }} \end{array}} \right]. $ |
式中:
| 表 2 RSSR机构惯性参数 Table 2 Inertial parameters of RSSR |
Baumgarte约束稳定是一个简单易用的动力学修正方法,以消除和改善常规拉格朗日乘子法在应用于特殊场合时算法上的缺陷,方法中添加了两个位置和速度约束的反馈控制常数α、β.此时拉格朗日乘子法公式中的γ将被扩展,并重新写作
| $ \gamma ' = \gamma - 2\alpha \mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }} - {\beta ^2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}. $ |
含间隙关节研究中,接触力模型的建立也是重要的研究内容,对于含间隙的球关节,球窝与球头之间的接触可以用经典的Hertz接触模型来描述为
| $ {F_n} = K{\delta ^n}, $ |
式中,K为接触刚度系数,δ为嵌入深度,n设定为1.5. K依赖于接触的材料与接触面的几何特性.对于球面接触,接触刚度系数一般给定为
| $ K = \frac{4}{{3\left( {{\sigma _i} + {\sigma _j}} \right)}}{\left[ {\frac{{{R_i}{R_j}}}{{{R_i} + {R_j}}}} \right]^{\frac{1}{2}}}. $ |
式中,与材料有关的参数σi, σj给定为
| $ {\sigma _k} = \frac{{1 - \nu _k^2}}{{{E_k}}}.\left( {k = i,j} \right) $ |
式中,νk, Ek分别为与接触球面相关的泊松比和杨氏模量. Hertz接触模型为纯弹性接触,没考虑能量耗散问题,适用于嵌入深度较小的场合.只考虑材料弹性变形的接触力模型虽然简单,但对碰撞过程的描述不准确,在碰撞过程中如不考虑能量耗散问题,分析结果可能失真.学者Lankarani和Nikravesh提出L-N非线性连续接触力模型,该模型考虑了碰撞过程中的能量耗散,反映出碰撞体的材料特性、几何特征以及运动状态对碰撞过程的影响. L-N接触力公式可表示为
| $ {F_n} = K{\delta ^n} + D\dot \delta , $ |
D的表达式为
| $ D = \frac{{3K\left( {1 - c_e^2} \right)\dot \delta }}{{4{{\dot \delta }^{\left( - \right)}}}}. $ |
式中:ce为恢复系数,
| $ {F_n} = K{\delta ^n}\left[ {1 + \frac{{3\left( {1 - c_e^2} \right)\dot \delta }}{{4{{\dot \delta }^{\left( - \right)}}}}} \right]. $ |
在图 3中,在C点处,假设构件3与构件4联接的球关节含有间隙,不考虑摩擦的影响.由于间隙的存在,使得关节对构件的约束由运动约束转变为力约束,系统受到了额外的附加力,接触碰撞力为fN=Fnn.以拉格朗日乘子法建立的动力学方程调整为
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&{{\mathit{\boldsymbol{C}}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{C}}_c}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot q}}}\\ \mathit{\boldsymbol{\lambda }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_c}}\\ {\gamma - 2\alpha \mathit{\boldsymbol{ \boldsymbol{\dot \varPhi} }} - {\beta ^2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \end{array}} \right]. $ |
式中,下角标c表示为含间隙系统下的参数. Fc包括作用在机构上的广义外力以及接触碰撞力fN的广义力. RSSR机构中运动约束方程组Φ中需要去掉与含间隙球关节相关的约束方程Φ3.为验证力学模型与计算方法的准确性,首先采用较为简单的赫兹接触力模型进行计算,曲柄驱动采用PD控制方法,位置增益kp及速度增益kv系数见表 3.动力学方程数值求解采用R-K定步长积分方法,积分步长为ts.机构几何参数以及惯性参数见表 1,表 2;含球关节间隙以及接触力所需的相关参数见表 3.
| 表 3 含间隙RSSR机构仿真参数 Table 3 Simulation parameters of RSSR mechanism with joint clearance |
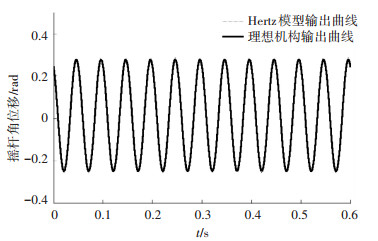
当曲柄转动速度为1 200 r/min时,球关节含间隙情况下,机构摇杆的角位移、速度加速度输出如图 4,图 5所示.
|
图 4 输出角随时间变化规律图 Figure 4 Change regulation of output angle |
|
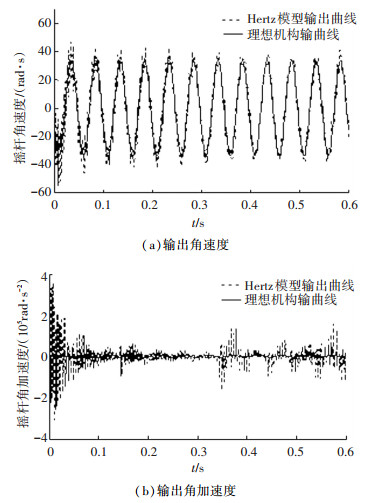
图 5 输出角速度、角加速度随时间变化规律图 Figure 5 Change regulation of output angle velocity and acceleration |
由以上仿真结果可以得知,当间隙存在时,对输出的角位移影响较弱,对速度的影响较大,影响尤其显著的是角加速度,可以从图中间接知道,关节副元素之间存在高频的冲击力.
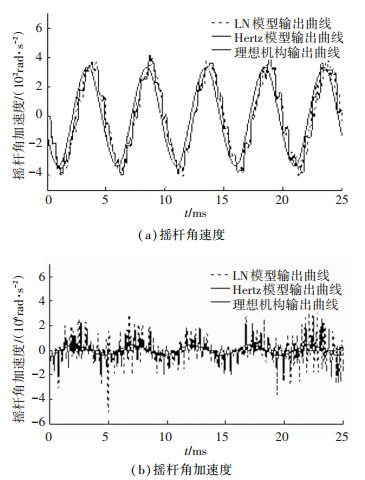
3.2 接触力模型影响分析转速12 000 r/min,间隙量0.5mm(其他参数同表 1~3)时,Hertz模型与L-N模型的动力学输出曲线仿真对比,仿真时长为0.025 s.从图 6中可以看出,L-N模型的加速度仿真结果其峰值要大于Hertz模型.
|
图 6 摇杆角速度、角加速度随时间变化对比图 Figure 6 Output angle velocity and acceleration |
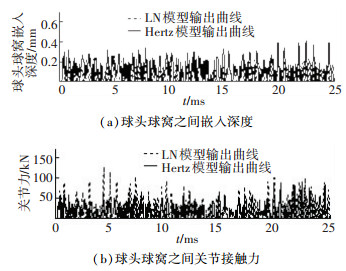
在图 7中,由于L-N模型考虑了碰撞过程中能量损失的存在,在嵌入深度的对比中,在Hertz模型中出现了大量嵌入深度峰值极高的尖点,L-N模型中考虑了碰撞体的材料特性,局部变形和碰撞速度等信息,其模拟出的嵌入深度要小于Hertz模型,关节接触力峰值大于Hertz模型.因此,可以得出在含球关节间隙的RSSR机构中,两种模型将对仿真的部分输出结果会产生较大的影响.
|
图 7 球头球窝之间嵌入深度、关节接触力对比图 Figure 7 Penetration depth and contact force |
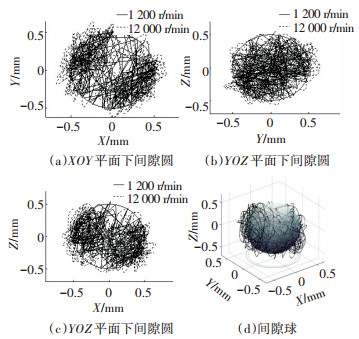
在RSSR等诸多含曲柄机构中,曲柄输入转速的设置对机构的惯性力分布情况产生直接影响,进而对机构的输出单元,连接构件等动力学特性产生影响.对不同曲柄输入转速下动力学输出曲线进行对比分析,关节力采用Hertz接触模型.参数选取为:关节间隙量为0.5 mm,转速分别选取为1 200 r/min,12 000 r/min. 图 8反映了C点处球关节球头中心相对于球窝中心的运动轨迹,在间隙量为0.5 mm状态下,转速无论1 200 r/min亦或是12 000 r/min,球头相对球窝仍是分离状态占大多数时间.球头中心运动轨迹多在间隙空间内,碰撞点集中在间隙圆附近,在间隙球的两个区域分布较为密集,与RSSR机构连杆和摇杆的运动时受到的约束相关.
|
图 8 不同转速下间隙圆、间隙球对比图 Figure 8 Clearance circle and ball at different input speeds |
间隙尺寸的出现是造成含关节间隙多体系统输出呈现特殊规律的直接原因,本小节将对含不同球关节间隙量的RSSR空间机构输出动态特性进行对比分析,探究间隙量的变化对机械系统动力学输出特性的影响规律.首先选取间隙量为0.5和0.1 mm进行对比.
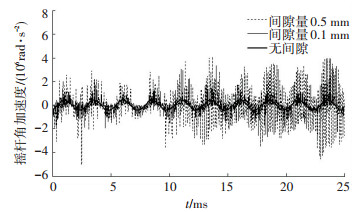
如图 9,间隙量的调整可以显著地改变系统的动力学输出特性.比较球关节间隙0.5 mm和0.1 mm时摇杆的输出加速度,通过观察发现,曲柄几个转动周期后,0.5 mm间隙量时的摇杆输出加速度曲线毛刺现象变得极为剧烈,且呈现放大的趋势,而间隙量为0.1 mm时加速度的变化较为稳定,可见间隙量的大小深刻影响着机构的动态特性.
|
图 9 间隙量0.5 mm和0.1 mm输出加速度对比图 |
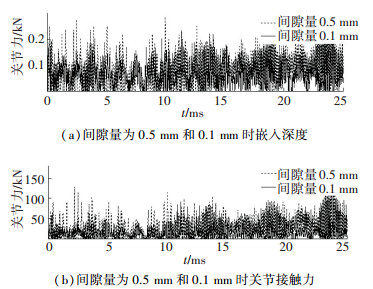
图 10所示球头相对球窝嵌入深度可以发现,间隙量的大小同样能够影响间隙运动副之间的碰撞剧烈程度,间隙量减小,嵌入深度减小. 图 10所示接触力的变化趋势同样符合预期,间隙量由0.5 mm减小到0.1 mm后,显著改善了关节受到高频剧烈撞击力的情况.
|
图 10 间隙量为0.5 mm和0.1 mm时嵌入深度、关节接触力对比图 Figure 10 Penetration depth and contact force at 0.5 mm and 0.1 mm clearance |
进一步仿真可以发现,虽然随着间隙量的减小,加速度曲线的毛刺现象得到了进一步抑制, 但间隙量同样减小5倍,由0.1 mm减少到0.02 mm时,间隙量对加速度曲线震荡峰值抑制效果没有0.5 mm减少到0.1 mm时明显.间隙量为0.1~0.02 mm对比时,球头球窝之间的嵌入深度、接触力同样没有0.5~0.1 mm对比时明显.间隙量为0.02 mm时,球头与球窝之间的嵌入深度峰值仅比间隙量为0.1 mm时的嵌入深度减少约10%~20%.当系统运转稳定后,0.1 mm间隙所产生的接触力相比于0.02 mm间隙产生的接触力约大1倍.同时,随着间隙量的进一步减小,球头球窝嵌入深度与接触力曲线呈现出了更明显的规律性.
通过间隙量对系统输出影响的分析,我们得到了相当多的信息.在其他条件不变的情况下,间隙量在最初的减小过程中可以显著抑制由间隙带来的种种不利.但当间隙量继续减少时,通过调整间隙量起到的稳定系统的作用将有所下降.间隙量的减小有助于更加系统地分析关节间碰撞力的变化规律.
4 结论本文采用拉格朗日乘子法,建立了理想的RSSR空间机构的动力学模型,在PD控制方法驱动下,正动力学仿真结果与运动学结果比较,验证了动力学建模的正确性;进一步建立了含单个球关节间隙的RSSR空间机构动力学模型,采用R-K数值方法,得出在含间隙情况下RSSR机构的动态特性规律;对Hertz和L-N碰撞接触模型、曲柄输入转速以及关节间隙尺寸因素对机构的动态输出产生的影响进行了深入的分析.得出如下结论:
1) L-N接触力模型相对于Hertz模型,由于考虑接触碰撞过程中能量的损失,在仿真计算过程中的计算得出嵌入深度小于Hertz模型下的嵌入深度;关节接触力峰值大于Hertz模型下的接触力峰值.
2) 曲柄转速的增大,球关节接触力加大,嵌入深度增加,球头与球窝的碰撞接触点主要分布于间隙球的两个局部区域,与机构的连杆与摇杆的运动规律相关.
3) 球关节间隙对机构摇杆的位置输出有显著的影响;对摇杆加速度的输出影响尤为剧烈;随着间隙量的进一步减小,通过减小间隙量起到稳定系统的作用不显著.
以上分析结果对于含球关节间隙空间机构的结构设计、额定工作转速范围的选取以及球关节制造加工工艺、精度要求等均有指导价值.
| [1] |
SUN Dongyang, CHEN Guoping, WANG Tiecheng. Wear prediction of a mechanism with joint clearance involving aleatory and epistemic uncertainty[J]. Journal of Tribology, 2014, 136: 041101-1. DOI:10.1115/1.4027607 |
| [2] |
白争锋. 考虑铰间间隙的机构动力学特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2011: 5-20. BAI Zhongfeng. Research on dynamic characterisitcs of mechanism with joint clearance[D]. Harbin: Harbin Institutes of Technology, 2011: 5-20. |
| [3] |
FLORES P, AMBRSIO J, CLARO J. Kinematics and dynamics of multibody systems with imperfect joints: models and case studies[M]. Berlin: Springer-Verlag, Heidelberg, 2008: 2-3.
|
| [4] |
TASORA A, PRATI E, SILVESTRI M. A compliant measuring system for revolute joints with clearance[C]// International Conference on Tribology. Parma: AITC-AIT, 2006: 4-10.
|
| [5] |
FLORES P. Modeling and simulation of wear in revolute clearance joints in multibody systems[J]. Mechanism and Machine Theory, 2009, 44: 121-122. |
| [6] |
TASORA A, PRATI E, SILVESTRI M. Experimental investigation of clearance effects in a revolute joint[J]. Journal of Clinical Virology, 2009, 44(8): 19-20. |
| [7] |
ERKAYA S, UZMAY I. Investigation on effect of joint clearance on dynamics of four-bar mechanism[J]. Nonlinear Dynamics, 2009, 58: 179-198. DOI:10.1007/s11071-009-9470-7 |
| [8] |
SHIAUT, TSAI Y, TSAI M. Nonlinear dyanmic analysis of a parallel mechanism with consideration of joint effects[J]. Mechanism and Machine Theory, 2008, 43: 491-505. DOI:10.1016/j.mechmachtheory.2007.03.008 |
| [9] |
FLORESP, LANKARANI H M. Spatial rigid-multibody systems with lubricated spherical clearance joints: modeling and simulation[J]. Nonlinear Dynamics, 2010, 60(1): 99-114. |
| [10] |
FLORES P, LANKARANI H M. Dynamic response of multibody systems with multiple clearance joints[J]. Journal of Computational & Nonlinear Dynamics, 2012, 7(3): 636-647. |
| [11] |
MUVENGEIO, KIHIU J, IKUA B. Numerical study of parametric effects on the dynamic response of planar multi-body systems with differently located frictionless revolute clearance joints[J]. Mechanism and Machine Theory, 2012, 53: 30-49. DOI:10.1016/j.mechmachtheory.2012.02.007 |
| [12] |
赵刚练, 姜毅, 郝继光. 考虑圆柱铰链间隙的多刚体系统动力学计算方法[J]. 振动与冲击, 2013, 32(17): 171-176. ZHAO Ganglian, JIANG Yi, HAO Jiguang. Computational method of rigid multibody system dynamics considering cylindrical joint clearance[J]. Journal of Vibration and Shock, 2013, 32(17): 171-176. DOI:10.3969/j.issn.1000-3835.2013.17.033 |
 2018, Vol. 50
2018, Vol. 50


