近年来能源价格和减排压力日益增长,耗能占全国可消费能源总量的72.8%[1]的制造工业面对环境压力, 迫切需要重新考虑能源的利用和节省.与此同时,消费者对于多样和个性化商品的需求吸引着制造业不断加快产品更新迭代,使得废旧产品的环境问题受到极大关注,带来了再制造产业的快速发展.一项关于汽车零部件的研究表明[2], 再制造产品可以节约大致85%的制造过程中的能量耗费.行业利益主要来自于再次使用旧部件得到的能源和材料的节省,进而节约了制造过程的固有成本.
再制造系统一般分为废旧产品的分解、重加工和重组装3个子系统[3].目前的再制造相关研究多集中于产品工艺[4]和定价策略[5],而对于再制造生产系统的调度和计划大多关注单一的再制造子系统.例如:Kalaci[6]考虑了序列独立的再制造分解子系统的生产线平衡问题, 提出结合可变邻域搜索的遗传算法求解多目标调度问题.对于重加工子系统,Yu等[7]在定义了加工车间调度问题后提出了多种调度算法,定义中调度的任务被分组为作业组在各重加工车间被独立加工,即带有作业组的加工车间调度.之后,Kim等[8]通过考虑依赖于产品序列的准备时间拓展了基础模型. Oh[9]提出了一个基于图像的优化模型同时进行再制造重组装和采购计划,以决定部件组装和采购的数量.少有文献考虑完整的再制造系统调度,也较少加入能源因素的考量.
然而能源因素在其他生产系统中已经被大量研究,产生了大量具备借鉴意义的方法和策略. Mouzon[10]通过判断处于闲时的非瓶颈机器是否适当关机实现单机总能源消耗最小,可以节省开关机和闲置过程80%的能源消耗. Luo[11]针对混合型流水线考虑生产效率的同时考虑电价表,提出最小化电力成本的双目标蚁群算法.
由文献[12]可知,一阶段多机二阶段单机的两阶段流水线装配问题若不考虑能耗已属NP-hard问题,Kim尝试使用CPLEX解决包含20件产品3个部件的小规模问题,也无法在一小时内解决.本文研究的问题在此基础上考虑更多因素变得更为复杂,显然也属NP-hard问题,采用解析方法无法求解中、大规模问题,目前大多数解决此类调度问题的方法都基于启发式算法实现.为此,本文考虑一个经典的带有流水线型重加工线的再制造系统,计算最小化最大完工时间的同时加入能耗考量,使用改进的多目标人工蜂群算法进行双目标调度研究.
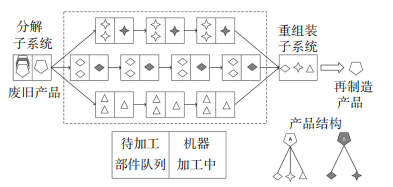
1 问题描述与数学建模 1.1 问题描述一个完整的再制造系统的通用模型中包含3个子系统——分解、重加工、重组装.本文的研究对象与典型再制造系统有所差异,重加工子系统中配置的不是加工车间而是多条专用流水线,见图 1.
|
图 1 带有流水线型重加工线的再制造系统配置 Figure 1 Remanufacturing system with parallel flow-shop-type reprocessing lines |
本文考虑系统的一个静态确定性版本,即问题中涉及的所有具有不确定性的输入数据都被提前给出.由于分解、重加工、重组装操作的换模时间独立于每个操作,因此被包括在每一个对应操作中的时间当中而不额外计算.研究中不考虑工艺缺陷,所有分解得到的部件在经过重加工以后都成为合格部件,可以重新组装得到合格的再制造产品.假设机器在开关机和加工过程中功率均匀.
系统的详细运作步骤如下:
1) 系统初始阶段共有n件产品,按一定的顺序排列依次送入再制造系统.
2) 每一件废旧产品进入系统后,首先在分解子系统被分解成其组成部件,其中核心部件被送入下一环节进行重加工.分解子系统对任意两件先后进入的产品处理没有交叉.
3) 每一条重加工线都专属修复一种部件,每件产品被分解后所得核心部件将进入对应的重加工线进行重加工.每一条重加工线上的每一个工作站只有加工完当前部件后,才会开始加工等待队列中的部件.等待队列中部件的顺序由其所属产品的分解顺序决定.
4) 当一件产品分解所得的所有核心部件被重加工完全,重组装子系统会根据成套部件最先可用的顺序将产品组装为合格的再制造产品.
因此, 本文研究的问题可被描述如下:对于一组给定的废旧产品,以最小化最大完工时间和系统能耗为目标,决定分解子系统中将被分解的产品序列,流水线型重加工线每个工作站上将被重加工的部件序列,被重组装的产品序列,及每个作业的完成时间.为便于形式化描述,定义符号及参数如下:
i=1, 2, …, n:产品序号.
j=1, 2, …, m:部件(重加工线)序号.
k=1, 2, …, lj:重加工线j上的工作站数.
tiD:分解产品i所需时间.
tijkR:重加工线j的工作站k加工产品i的部件j所需时间.
tiA:重组装产品i所需时间.
tDon, tjkRon, tAon:所有机器开机所需时间.
tDoff, tjkRoff, tAoff:所有机器关机所需时间.
piD:分解产品i所需功率.
pijkR:重加工线j的工作站k加工产品i的部件j所需功率.
piA:重组装产品i所需功率.
ponD, pjkRon, ponA:所有机器开机所需功率.
pDoff, pjkRoff, pAoff:所有机器关机所需功率.
pDidle, pjkRidle, pAidle:所有机器闲时所需功率.
ND, NjkR, NA:所有的开关机次数.
M:一个极大的数.
决策变量如下:
CiD:产品i的分解完成时间.
CijkR:重加工线j工作站k上重加工产品i的部件j的完成时间.
CiA:产品i的重组装完成时间.
CiM:产品i的所有重加工部件在对应重加工线的末工作站上完成时间的最大值.
xii′:如果产品i恰好在产品i′之前被分解,则值取1,否则值取0.
yii′jk:在重加工线j工作站k上,如果产品i对应的部件恰好在产品i′对应的部件之前被重加工,则值取1,否则值取0.
zii′:如果产品i恰好在产品i′之前被重组装,则值取1,否则值取0.
1.2 数学模型根据问题描述、假设以及符号定义,系统问题的建模如下:
目标函数:
| $ {\rm{Min}}F = \left( {{f_1},{f_2}} \right), $ | (1) |
| $ {f_1} = {\rm{Minimize}}\;\mathop {\max }\limits_i C_i^{\rm{A}}, $ | (2) |
| $ {f_2} = {\rm{Minimize}}E\;{C^{\rm{D}}} + \sum\limits_{j = 1}^m {\sum\limits_{k = 1}^{{l_j}} {E\;C_{jk}^{\rm{R}}} } + E\;{C^{\rm{A}}}. $ | (3) |
式中:
| $ \begin{array}{l} E{C^{\rm{D}}} = \sum\limits_{i = 1}^n {p_i^{\rm{D}}} \cdot t_i^{\rm{D}} + p_{{\rm{idle}}}^{\rm{D}} \cdot t_{{\rm{idle}}}^{\rm{D}} + \\ \;\;\;\;\;\;\;\;\;\;{N^{\rm{D}}} \cdot \left( {p_{{\rm{on}}}^{\rm{D}} \cdot t_{{\rm{on}}}^{\rm{D}} + p_{{\rm{off}}}^{\rm{D}} \cdot t_{{\rm{off}}}^{\rm{D}}} \right), \end{array} $ |
| $ \begin{array}{l} EC_{jk}^{\rm{R}} = \sum\limits_{i = 1}^n {p_{ijk}^{\rm{R}}} \cdot t_{ijk}^{\rm{R}} + p_{{\rm{idle}},jk}^{\rm{R}} \cdot t_{{\rm{idle}},jk}^{\rm{R}} + \\ \;\;\;\;\;\;\;\;\;\;N_{jk}^{\rm{R}} \cdot \left( {p_{{\rm{on,}}jk}^{\rm{R}} \cdot t_{{\rm{on,}}jk}^{\rm{R}} + p_{{\rm{off,}}jk}^{\rm{R}} \cdot t_{{\rm{off,}}jk}^{\rm{R}}} \right), \end{array} $ |
| $ \begin{array}{l} E{C^{\rm{A}}} = \sum\limits_{i = 1}^n {p_i^{\rm{A}}} \cdot t_i^{\rm{A}} + p_{{\rm{idle}}}^{\rm{A}} \cdot t_{{\rm{idle}}}^{\rm{A}} + \\ \;\;\;\;\;\;\;\;\;\;{N^{\rm{A}}} \cdot \left( {p_{{\rm{on}}}^{\rm{A}} \cdot t_{{\rm{on}}}^{\rm{A}} + p_{{\rm{off}}}^{\rm{A}} \cdot t_{{\rm{off}}}^{\rm{A}}} \right). \end{array} $ |
约束如下:
| $ C_i^{\rm{D}} \ge t_i^{\rm{D}}{\rm{for}}\;{\rm{all}}\;i, $ | (4) |
| $ \begin{array}{l} C_{i'}^{\rm{D}} - C_i^{\rm{D}} + M \cdot \left( {1 - {x_{ii'}}} \right) \ge t_{i'}^{\rm{D}},\\ {\rm{for}}\;{\rm{all}}\;i\;{\rm{and}}\;i'\left( {i \ne i'} \right), \end{array} $ | (5) |
| $ \begin{array}{l} C_i^{\rm{D}} - C_{i'}^{\rm{D}} + M \cdot {x_{ii'}} \ge t_i^{\rm{D}},\\ {\rm{for}}\;{\rm{all}}\;i\;{\rm{and}}\;i'\left( {i \ne i'} \right), \end{array} $ | (6) |
| $ C_{ij1}^{\rm{R}} \ge C_i^{\rm{R}} + t_{ij1}^{\rm{R}}\;{\rm{for}}\;{\rm{all}}\;i\;{\rm{and}}\;j, $ | (7) |
| $ \begin{array}{l} C_{ij,k + 1}^{\rm{R}} \ge C_{ijk}^{\rm{R}} + t_{ij,k + 1}^{\rm{R}},\\ {\rm{for}}\;{\rm{all}}\;i,j\;{\rm{and}}\;k = 1,2, \cdots ,{l_j} - 1, \end{array} $ | (8) |
| $ \begin{array}{l} C_{ijk}^{\rm{R}} - C_{i'jk}^{\rm{R}} + M \cdot {y_{ii'jk}} \ge t_{ijk}^{\rm{R}},\\ {\rm{for}}\;{\rm{all}}\;i,i'\left( {i \ne i'} \right),j\;{\rm{and}}\;k, \end{array} $ | (9) |
| $ \begin{array}{l} C_{ijk}^{\rm{R}} - C_{i'jk}^{\rm{R}} + M \cdot {y_{ii'jk}} \ge t_{ijk}^{\rm{R}},\\ {\rm{for}}\;{\rm{all}}\;i,i'\left( {i \ne i'} \right),j\;{\rm{and}}\;k, \end{array} $ | (10) |
| $ C_i^{\rm{M}} \ge C_{ij{l_j}}^{\rm{R}},{\rm{for}}\;{\rm{all}}\;i\;{\rm{and}}\;j, $ | (11) |
| $ C_i^{\rm{A}} \ge C_i^{\rm{M}} + t_i^{\rm{A}},{\rm{for}}\;{\rm{all}}\;i, $ | (12) |
| $ C_{i'}^{\rm{A}} - C_i^{\rm{A}} + M \cdot \left( {1 - {z_{ii'}}} \right) \ge t_{i'}^{\rm{A}},{\rm{for}}\;{\rm{all}}\;i, $ | (13) |
| $ C_{i'}^{\rm{A}} - C_i^{\rm{A}} + M \cdot \left( {1 - {z_{ii'}}} \right) \ge t_{i'}^{\rm{A}},{\rm{for}}\;{\rm{all}}\;i, $ | (14) |
| $ \begin{array}{l} {x_{ii'}},{y_{ii'jk}},{z_{ii'}} \in \left\{ {0,1} \right\},\\ {\rm{for}}\;{\rm{all}}\;i,i'\left( {i \ne i'} \right),j\;{\rm{and}}\;k. \end{array} $ | (15) |
其中式(1)、(2)、(3)为模型的目标函数,约束(4)表示分解一件产品的完成时刻大于等于其分解时间.约束(5)、(6)确保了分解阶段中没有任何两件产品的操作会被同时进行,即分离约束.而约束(9)、(10)和约束(13)、(14)分别表示重加工子系统和重组装子系统的分离约束.约束(7)确保每件产品的每个部件的首个重加工任务必须要在所属产品的分解任务完成之后开始.约束(8)表示每条重加工线上工作站的顺序被提前确定,即连接约束.约束(11)规定产品的所有重加工部件在对应重加工线的末工作站上加工完成时间的最大值.约束(12)规定每件产品的重组装任务必须在其所有重加工部件完成重加工以后开始.约束(15)表示0-1决策变量.
2 改进多目标人工蜂群算法Karaboga[13]首创提出人工蜂群算法(artificial bee colony algorithm, ABC)优化多变量和多模连续函数,其相比于其他基于种群的元启发式算法涉及变量少得多,因此易于执行且更适应于工程应用.此前的研究[14]已经表明ABC算法在参数设置上具有优秀的鲁棒性,通过适当修改后能够有效且快速收敛,得到了广泛的应用.因此,本文将ABC算法作为主体,结合吸收了演进算法的诸多优势,构建了一种改进的多目标人工蜂群算法,并利用模拟退火算法求解能耗子问题.
2.1 标准人工蜂群算法受到蜂群的智能觅食行为的启发,ABC算法将觅食的人工蜂分为三个群体,雇佣蜂指的是开发蜜源的蜂种;观察蜂指的是等待在蜂巢当中接受雇佣蜂的信息决定选择的蜜源的蜂种;侦查蜂指的是随机搜索新蜜源的蜂种.
标准ABC算法生成一定数量初始解后评估其适应值.根据适应值指派雇佣蜂进行邻域搜索产生新解,并评估其适应值决定是否采纳新解.雇佣蜂将适应值信息传回蜜源,由此计算观察蜂跟随每个雇佣蜂对应蜜源的概率值.轮盘赌跟随蜜源后,观察蜂在其周围产生新的邻域解,评估适应值决定是否采纳新解.之后,根据每一个当前解被尝试的次数是否超过限制决定是否将其抛弃,若抛弃则派出侦查蜂随机发现新的蜜源.若终止条件未满足,回到雇佣蜂邻域搜索阶段;否则,停止程序并输出当前最佳蜜源.
2.2 改进多目标人工蜂群算法改进多目标人工蜂群算法(improved multi-objective artificial bee colony algorithm, IMOABC)基于标准ABC算法设计,使用了一个全局精英解集来储存搜索阶段的非支配解.以下初始参数被提前设置:蜜蜂种群数量(P);尝试次数限制(L),一个可行解的尝试次数一旦超过此值,即被放弃;精英种群数量(E);最大循环次数(C).
2.2.1 编码与初始化根据排序问题特性,问题可行解的形式是一个产品进入分解子系统的序列,对应一个种群个体,即种群个体采用排列编码.而所有产品在每个机器上的加工完成时间矩阵作为解码结果.
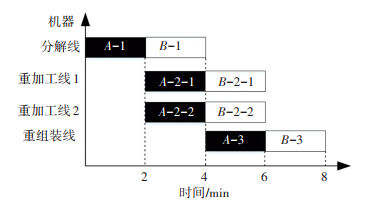
假设有2件产品,2条重加工线,每条线上1台机器的场景下一个可行序列为X={A, B}(见图 2). 2件产品在所有机器上加工时间是2 min,则解码为
| $ \mathit{\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} 2&4&4&6\\ 4&6&6&8 \end{array}} \right]. $ |
|
图 2 示例甘特图 Figure 2 Exemplary gantt chart |
完成时间数据根据产品序列满足模型约束得到.
标准ABC算法采用随机方式生成初始种群,该方法虽可覆盖较大的解空间有利于全局优化,但难以保证初始解的质量,为后续搜索增加了难度.因此,IMOABC中引入NEH启发式方法[15],建立基于NEH和随机方法的混合方法产生初始种群. NEH方法中,首先将所有工件按总加工时间递减排序,选择前两个工件经比较保留完成时间最短的序列;其次将第三个工件插入序列中的各个位置,同样保留完成时间最短的序列;最后将剩余工件重复上步操作,得到一个可行解作为首个初始解,在这个解的基础上进行少量成对互换生成P/4个的初始解,其他个体则采用随机方法生成.每个蜜源会被指定一个标志向量记录其被尝试次数,以此为依据在每次迭代中判定尝试次数超过L的蜜源会被废弃.
初始化阶段,所有的非支配解都会被加入到精英解集中.其中针对每个解都会计算并指定一个拥挤距离,代表一个解周围存在其他个体的密集程度.这个值决定了同一精英解集中的非支配解间的优先关系.
2.2.2 拥挤距离指定这里使用的拥挤距离计算方法与非支配排序遗传算法(non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ)[16]相似:首先,将精英种群中的所有解按照每个目标函数值升序排列;接着,对于每个目标函数,为序列的边缘解(函数值最大和最小的解)指定拥挤距离为负无限;之后,所有其他解的拥挤距离D指定为
| $ {D_i} = {D_{1,i}} + {D_{2,i}}. $ |
例如,解在第一个目标函数上的拥挤距离D1, i为
| $ {D_{1,i}} = \frac{{\left| {f_{1,i - 1}^{\rm{S}} - f_{1,i}^{\rm{S}}} \right| + \left| {f_{1,i + 1}^{\rm{S}} - f_{1,i}^{\rm{S}}} \right|}}{{f_{1,{\rm{end}}}^{\rm{S}} - f_{1,{\rm{1}}}^{\rm{S}}}}. $ |
式中,f1, iS表示第一个目标函数中升序排列第i位的解,而f1, endS和f1, 1S为此时的边缘解.
一个解距离两侧的解越远,所处的空间越空旷,对应的拥挤距离值越大,在择优中优先级更高,其中精英解集中优先级最高的解称为当前精英解.而边缘解由于其无穷小的拥挤距离不被选择.之后任何一个非支配解集的内部优先级的比较都采用拥挤距离作为指标.
2.2.3 雇佣蜂部分算法雇佣蜂承担了优秀解的搜索任务.所有雇佣蜂开始在当前指定的蜜源邻域内生成新的邻域蜜源.对于基于序列的邻域结构,一般使用插入算子或交换算子作用于旧蜜源来生成新的邻域蜜源,本文用于产生邻域解的方式是在当前解序列内随机选取n/4个位置换取序列中其他位置的值使之与当前精英解保持一致,被选取位原值填补对应空缺位.之后将这个邻域解临时加入到精英解集中进行Pareto排序,若不被精英解集中任何解支配的解则保留,同时排除其支配的解,更新蜜源.一旦加入后导致精英解集大小超过E,则参考拥挤距离将低优先级的解淘汰以保持规模.如果蜜源被更新,则对应邻域搜索次数的标志向量置0,否则,增加1.
2.2.4 观察蜂部分算法一次迭代中所有雇佣蜂对应蜜源的适应值计算完毕以后,观察蜂根据蜜源适应值大小决定选择的概率.蜜源通过Pareto排序和拥挤距离指定排序,第i位蜜源被选择的概率Gi定义为
| $ {G_i} = \frac{{2\left( {P + 1 - i} \right)}}{{P\left( {P + 1} \right)}}. $ |
为了避免低效重复雇佣蜂阶段邻域搜索,观察蜂达到选择蜜源后,采用不同的邻域搜索方式:另行选择一个非对应蜜源的可行解后在当前解序列内随机选取n/4个位置换取序列中其他位置的值使之与可行解保持一致,被选取位原值填补对应空缺位.之后再用与雇佣蜂阶段相同的方式更新精英解集.如果对应蜜源被更新,则对应邻域搜索次数的标志向量置0,否则,增加1.
2.2.5 侦察蜂部分算法标准ABC算法中随机生成新解的侦查蜂策略单一简陋,所得结果与多代进化又位于更有前景邻域的雇佣蜂相比,竞争力差,故难以在下一代成功存活.因此本文改用当前精英解作为侦查蜂全局探索的基础,对其解序列执行n/4次随机交换的方式产生邻域解.由于初始解中已经包括了质量较高的NEH启发式算法得到的解,为了避免算法早熟,IMOABC不限制侦查蜂个数,只要尝试次数超过L的蜜源上的雇佣蜂都会转化为侦查蜂.
2.3 模拟退火算法求解能耗子问题对于一个可行解而言,如果重加工子系统中不出现任何等待,机器一旦空闲立即加工等待队列中的首个部件,这样得到的所有完成时间结果将其称作“前置调度”.由于重组装子系统的成套要求,一件产品所属的所有核心部件的重加工完成时间只要赶在其中最大者之前就不会影响对应的重组装任务开始,因此放松立即加工队列中首个部件这一要求,调整所有部件重加工时间至不影响重组装任务下的最迟时刻所得到的结果称作“后置调度”.研究假设先利用前置调度得到一组所有任务的完成时间,固定其中的分解任务和重组装任务完成时间后仅允许重加工子系统中任务可变动.它们在两类调度结果之下完成时间可能存在大小不同的可变动范围,变动会影响能源消耗量,并且决策之间相互影响.由此可得其计算复杂度为O(ln),其中n为任务数,l为任务的可变动范围大小,l=
系统能源耗的计算中,所有机器上任务的完成时间确定后,对于每一个机器闲时,本文采用Mouzon[10]的开关机指定策略结合机器自身的耗能属性来判断这个闲时长度是否执行一次开关机操作,最后汇总每一台机器的耗能得到系统能耗.
2.4 IMOABC伪代码研究提出的IMOABC伪代码见图 3.

|
图 3 IMOABC伪代码 Figure 3 Pseudocode of IMOABC |
所有算法基于Windows 10下MATLAB(2016b)环境编程实现,在主频3.7 GHz,内存为8 GB、Intel Core i5-4570 CPU的计算机上进行数值计算.
实验使用获得的Pareto解个数(NS)、解间距(SP)及运行时间(CPU)作为评价算法性能的指标,其中解间距为当次运行中除两端点外所有Pareto解的拥挤距离之和.根据实验设置P=30,L=3,E=30,C=50时,算法以较高质量求解问题.
为了测试提出的算法在求解问题中的表现,参考Kim[12]选取了8个产品数量和重加工线数量规模大小不同的算例,采用具有代表性的多目标优化NSGA-Ⅱ和IMOABC进行对比计算实验. 4个不同产品数量水平(n=20, 40, 60, 80)各自对应2个不同重加工线数量水平(m=3, 5, 7, 9),形成8个组合.研究考虑的是问题的一个确定性版本,因此每次测试数据都在计算开始前随机生成,这些数据包括每条流水线型重加工线上的机器数目、每个部件在每个子系统和每台机器上的加工时间.测试数据中,U[a, b]指范围[a, b]内的整数离散均匀分布.每条流水线型重加工线的机器的数量是由U[2, 4] (U[7, 9])生成,对应产品数量是20和40(60和80).此外,分解、重加工和重组装加工时间由U[10, 100]生成,机器的开关机时间由U[20, 50]生成,机器的加工功率由U[50, 100]生成,闲时功率由U[20, 50]生成,开关机功率由U[20, 80]生成.
3.2 数值计算由于此问题的真实Pareto前沿很难得到,本文采用以下方法获得近似前沿:算法独立运行多次后并记录每次的Pareto解集,从所有Pareto解集中获得新的Pareto解作为近似前沿.同时,本文将提出的IMOABC与目前在解决多目标问题上具有较优性能的经典算法即带精英策略的NSGA-Ⅱ对比,测试算法的性能.
为了验证研究考虑能耗的意义和使用开关机策略的有效性,表 1给出了在不考虑能源因素(null)、考虑能源因素但不使用开关机控制(energy)和考虑能源因素且使用开关机控制(on-off)3个策略下使用NSGA-Ⅱ求解10个随机加工序列在2个目标函数上的表现.加工序列的输入数据来自于(20, 3)下一组随机生成的测试数据.
| 表 1 3种策略下目标函数表现 Table 1 Objective performance under three strategies |
由表 1可以观察到,加入考虑能源因素后,在不影响最大完工时间的情况下,能耗量就可以得到大大削减.而且,加入在机器闲时判断是否执行开关机的策略以后,能源消耗量进一步减少,证明了所提出的节能策略的有效性.
为8个组合各随机生成一组输入数据,在on-off策略下分别运行IMOABC和NSGA-Ⅱ各10次后汇总得各自的Pareto解集,求解2个算法得到的2个目标的均值分别为
| $ {P_{2,I}} = \frac{{\overline {{f_{2,I,e}}} - \overline {{f_{2,I,o}}} }}{{\overline {{f_{2,I,e}}} }}, $ |
| $ {P_{2,N}} = \frac{{\overline {{f_{2,N,e}}} - \overline {{f_{2,N,o}}} }}{{\overline {{f_{2,I,e}}} }}. $ |
| 表 2 2种算法下使用开关机控制策略相对于不控制开关机策略的能源节约率 Table 2 Energy saving rate of using on-off strategy respect to null strategy under two algorithms |
由表 2可知,两种算法在使用开关机控制后都能在能源目标上取得更好的结果,同时,随着问题规模的增大,节约百分比逐渐减小.相比之下,IMOABC的节约比例更大,即得到的系统能耗更低.
为8个组合各随机生成10组输入数据,每组数据下分别运行IMOABC和NSGA-Ⅱ各10次后得到计算结果见表 3.由表 3可知,Pareto解的个数和解的间距指标上IMOABC都得到了优于NSGA-Ⅱ的结果,且差距没有随着问题规模的增大而劣化,体现了IMOABC的有效性和鲁棒性.尽管计算时间上IMOABC稍劣,但是这样程度的差距并无重大影响,且在调整算法的迭代次数后即可弥补.
| 表 3 不同规模问题的数值计算结果 Table 3 Numerical calculation results of different scale problems |
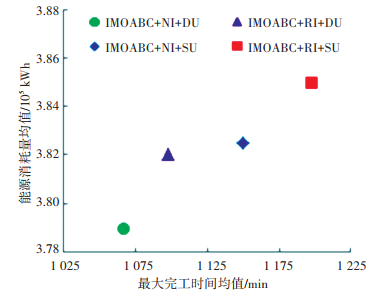
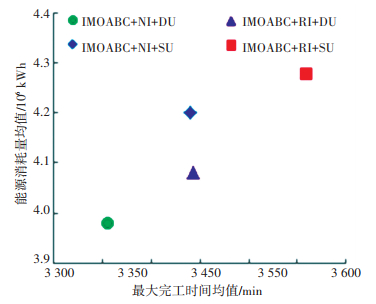
图 4和图 5分别以(20, 3)和(60, 7)下各一组随机生成的输入数据为例,给出了分别运行NEH算法参与得到初始解且改进更新精英解集方法的IMOABC(IMOABC+NI+DU)和随机得到初始解且改进更新精英解集方法的IMOABC(IMOABC+RI+DU)、NEH算法参与得到初始解但不改进更新精英解集方法的IMOABC(IMOABC+NI+SU)、随机得到初始解但不改进更新精英解集方法的IMOABC(IMOABC+RI+SU)各10次后汇总得各自的Pareto解集求得的2个目标的均值.计算结果证明提出的IMOABC性能的优越性归功于NEH算法参与得到的具有一定质量的初始解以及每次迭代中2种蜂采用不同方法更新Pareto精英解集.另外,稍加改进后更有竞争力的侦查蜂策略加强了算法的搜索能力.
|
图 4 算例(20, 3)下改进算法的目标函数表现 Figure 4 Objective performance of improved algorithm under example(20, 3) |
|
图 5 算例(60, 7)下改进算法的目标函数表现 Figure 5 Objective performance of improved algorithm under example(60, 7) |
图 6和图 7分别以(20, 3)和(60, 7)下各一组随机生成的输入数据为例,给出了分别运行MOABC和IMOABC各10次时的Pareto解的情况.可见问题规模较小时,IMOABC与NSGA-Ⅱ求得的解集存在一定相互支配和重合,但总体而言IMOABC得到的解集更优.随着规模扩大,IMOABC的Pareto解集逐渐占优,且差距增大, IMOABC性能的优越性逐步凸显.

|
图 6 算例(20, 3)的Pareto前沿 Figure 6 Pareto frontier of example(20, 3) |

|
图 7 算例(60, 7)的Pareto前沿 Figure 7 Pareto frontier of example(60, 7) |
1) 提出了一种改进的多目标人工蜂群算法,在融合NSGA-Ⅱ的排序规则的基础上,结合精英策略及两种更新方法保证了算法的收敛速度,结合双重邻域搜索、局部最优逃脱算子加强了算法的搜索能力.利用嵌入精英策略的模拟退火算法求解了能耗子问题,结合机器闲时关机的节能策略获得了大量的能源节约.
2) 数值计算验证了IMOABC具有较好的求解性能,表明算法的有效性和节能策略的可行性.
3) 研究补充了此类节能调度问题的研究短缺,实践者可以根据实际需求在一个目标上稍作退让以寻求另一目标的大幅优化,在利益与节能上寻找到所需的平衡点.
4) 未来研究可考虑放松由于成套组装而假设的重组装子系统时间固定约束,或者考虑从成套组装为出发点逆向进行系统调度,其他的再制造系统配置也迫切需要考虑能源因素的研究的大量开展.
| [1] |
周炳海, 苏谊. 基于可变缓冲区存储量的串行生产线节能分析[J]. 哈尔滨工程大学学报, 2016, 37(6): 832-836. ZHOU Binghai, SU Yi. Energy-saving analysis of serial production lines based on the changeable buffers'storage[J]. Journal of Harbin Engineering University, 2016, 37(06): 832-836. DOI:10.11990/jheu.201507085 |
| [2] |
PARKINSON H J, THOMPSON G. Analysis and taxonomy of remanufacturing industry practice[J]. Proceedings of the Institution of Mechanical Engineers Part E: Journal of Process Mechanical Engineering, 2003, 217(3): 243-256. DOI:10.1243/095440803322328890 |
| [3] |
V Daniel R Guide Jr. Production planning and control for remanufacturing: industry practice and research needs[J]. Journal of Operations Management, 2000, 18(4): 467-483. DOI:10.1016/S0272-6963(00)00034-6 |
| [4] |
WILSON J M, PIYA C, SHIN Y C, et al. Remanufacturing of turbine blades by laser direct deposition with its energy and environmental impact analysis[J]. Journal of Cleaner Production, 2014, 80(80): 170-178. DOI:10.1016/j.jclepro.2014.05.084 |
| [5] |
LI Xiang, LI Yongjian, CAI Xiaoqiang. Remanufacturing and pricing decisions with random yield and random demand[J]. Computers & Operations Research, 2015, 54: 195-203. DOI:10.1016/S1874-8651(10)60060-9 |
| [6] |
KALAYCI C B, POLAT O, GUPTA S M. A hybrid genetic algorithm for sequence-dependent disassembly line balancing problem[J]. Annals of Operations Research, 2016, 242(2): 321-354. DOI:10.1007/s10479-014-1641-3 |
| [7] |
YU J M, KIM J S, LEE D H. Scheduling algorithms to minimise the total family flow time for job shops with job families[J]. International Journal of Production Research, 2011, 49(22): 6885-6903. DOI:10.1080/00207543.2010.507609 |
| [8] |
KIM J S, PARK J H, LEE D H. Iterated greedy algorithms to minimize the total family flow time for job-shop scheduling with job families and sequence-dependent set-ups[J]. Engineering Optimization, 2017, 49(10): 1719-1732. DOI:10.1080/0305215x.2016.1261247 |
| [9] |
OH Y, BEHDAD S. Simultaneous reassembly and procurement planning in assemble-to-order remanufacturing systems[J]. International Journal of Production Economics, 2017, 184: 168-178. DOI:10.1016/j.ijpe.2016.12.009 |
| [10] |
MOUZON G, YILDIRIM M B, TWOMEY J. Operational methods for minimization of energy consumption of manufacturing equipment[J]. International Journal of Production Research, 2007, 45(18-19): 4247-4271. DOI:10.1080/00207540701450013 |
| [11] |
LUO Hao, DU Bing, HUANG G Q, et al. Hybrid flow shop scheduling considering machine electricity consumption cost[J]. International Journal of Production Economics, 2013, 146(2): 423-439. DOI:10.1109/ccdc.2008.4597463 |
| [12] |
KIM M G, YU J M, LEE D H. Scheduling algorithms for remanufacturing systems with parallel flow-shop-type reprocessing lines[J]. International Journal of Production Research, 2015, 53(6): 1819-1831. DOI:10.1080/00207543.2014.962112 |
| [13] |
KARABOGA D, BASTURK B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[J]. Journal of Global Optimization, 2007, 39(3): 459-471. DOI:10.1007/s10898-007-9149-x |
| [14] |
PAN Quanke, WANG Ling, LI Junqing, et al. A novel discrete artificial bee colony algorithm for the hybrid flowshop scheduling problem with makespan minimisation[J]. Omega, 2014, 45: 42-56. DOI:10.1016/j.omega.2013.12.004 |
| [15] |
NAWAZ M, ENSCORE E E Jr, HAM I. A heuristic algorithm for the m-machine, n-job flow-shop sequencing problem[J]. Omega, 1983, 11(1): 91-95. DOI:10.1016/0305-0483(83)90088-9 |
| [16] |
DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [17] |
DAI Min, TANG Dunbing, GIRET A, et al. Energy-efficient scheduling for a flexible flow shop using an improved genetic-simulated annealing algorithm[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(5): 418-429. DOI:10.1016/j.rcim.2013.04.001 |
 2018, Vol. 50
2018, Vol. 50


