当前国产数控车床运行故障多发,车床运行可靠性下降“发于内而形于外”,是系统组件独立故障和传播故障共同作用的结果.系统局部组件故障能够沿着多条路径逐步向其他组件扩散,少数具有高危害传播状态的路径甚至会引起整机瘫痪.进行数控车床故障传播机理分析,探寻数控车床运行可靠性下降的内因,是数控车床产业可靠性研究的重点和关键.
数控车床是集机、电、液、控于一体的复杂设备集成系统,组件单元间高耦合连接,影响作用形式多样.系统故障的层次性、传播性、并发性及不确定性等特征,使得系统故障传播机理分析愈加困难.得到正确的数控车床故障传播机理分析结论与事先建立完备的系统故障传播模型、评估综合表征故障传播行为的指标等工作密切相关.描述故障传播的模型很多,如Petri网、元胞自动机、拓扑网络模型、贝叶斯网等[1-4],这些方法多基于图论展开,但都不完全适用于本文研究对象.制约故障传播行为的影响指标众多,近年来研究发现,故障传播范围不局限于近邻,还可能呈现一定的远程联动关系[5],即处于故障传播模型结构中关键位置的组件,不仅仅能够将故障传至与之直接相连的组件,也可能影响到一些远程组件.传统基于故障概率、风险值或故障传播概率等单一指标研究数控车床故障传播行为[6-7],忽略模型结构特征影响,会导致一定误差产生,甚至得出错误结论.基于多指标的综合故障传播分析方法只见于电力、交通等网络[8-9].
本文结合数控车床组件运行故障信息,针对数控车床故障传播特点,基于图论中故障传播有向图模型[10],考虑系统结构特性,结合层次性分解技术,构建故障传播结构化、层次化模型,以描述数控车床组件故障的分步传播和扩散行为,且该模型不依赖于精确的数学模型,可实现快速建模及故障定位;考虑组件间故障传播概率、故障传播模型结构对故障传播行为的双重影响,评估综合表征故障传播行为的指标,识别系统关键节点及关键故障传播路径,从整体上研究故障发生的根本原因和内在传播机理,这对于提高故障诊断可信性、系统使用可靠性,保障大型复杂系统安全运行具有一定的指导意义.
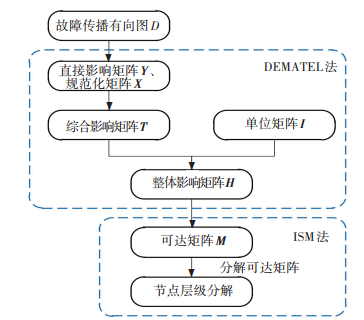
1 分层故障传播有向图模型构建首先以数控车床各个组件为节点集合V={v1, v2, …, vn},将组件间直接故障传播关系抽象为节点间互连的有向边集合E={ei→j}(1≤i, j≤n),构建系统故障传播有向图D=(V, E).进而集成DEMATEL/ISM方法分解模型D中各节点层级,层级分解流程如图 1所示.
|
图 1 集成DEMATEL/ISM的层级分解流程图 Figure 1 Hierarchy decomposition flow chart based on DEMATEL/ISM |
依据层级分解结果,提取骨架矩阵M′, 构建数控车床分层故障传播有向图模型D1,该模型可实现系统结构化和层次化,定位故障根源层组件,划分故障表层组件(故障多发层组件),同时明确组件间多层故障传播路径,为关键路径识别奠定基础.
2 故障传播概率评估 2.1 组件间故障影响度PageRank算法[11]是基于网络链接结构计算网页间相关性和重要性排名的一类算法,故引入PageRank算法度量某组件对其出链组件的故障影响度,定量分析组件间故障影响能力[12].
在相关假设条件下[13],故障传播有向图D=(V, E)中组件节点A的故障影响度(简称R值)的计算公式为
| $ R\left( A \right) = \frac{{\left( {1 - d} \right)}}{n} + d\sum\limits_{v \in O\left( A \right)} {\frac{{R\left( v \right)}}{{{I_v}}}} . $ | (1) |
式中:n为组件节点总数;d为阻尼因子,表示系统出现故障传播现象的概率,本文取传播故障数与总故障数的比值;O(A)为节点A的出链节点集合(即所有由节点A指出的节点集合);Iv为节点v的入链节点数量(即所有指向节点v的节点数量).
假设故障传播符合马尔科夫过程,因此定义一个n维向量,它的分量是各个组件的故障影响度值(记为R(vi)),即R=[R(v1), R(v2), …R(vn)]T.依据式(1),R值的矩阵化迭代计算方式为
| $ {\mathit{\boldsymbol{R}}^{x + 1}} = \frac{{1 - d}}{n}\mathit{\boldsymbol{e}} + d{\left( {\mathit{\boldsymbol{Q'}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{R}}^x}. $ | (2) |
式中:Rx+1、Rx分别表示第(x+1)次、第x次迭代所得各组件节点的故障影响度向量,e=(1, 1, …, 1)T,Q′为修正的状态转移概率矩阵(转置直接影响矩阵YT按行归一化得到矩阵Q,为了便于故障影响度计算,用向量(1/n,1/n,…,1/n)替换矩阵Q中元素全为0的行,得到修正的状态转移概率矩阵Q′).
ε为迭代收敛平稳阀值,赋予每个组件节点一个R初始值,当计算满足|Rx+1-Rx|<ε时,迭代结束,得到各个组件节点故障影响度R值.
若节点vi故障且能够将故障传至节点vj,则节点vi将获得部分R值,该值依赖于R(vj)和Ivj值大小;若R(vj)值较高,则R(vi)值也可能高,意味着连接两节点“输送故障”的有向边的故障影响度也可能高.依据该计算思想,结合数控车床分层故障传播有向图模型D1,定义组件间故障影响度为
| $ R\left( {{e_{i \to j}}} \right) = \sqrt {R\left( {{v_i}} \right)R\left( {{v_j}} \right)} . $ | (3) |
依据采集的故障数据评估各组件节点故障概率,进而融合组件间故障影响度表征组件间故障传播概率,组件vi故障对其出链组件vj的故障传播概率表示为
| $ P\left( {{e_{i \to j}}} \right) = {F_i}\left( t \right)R\left( {{e_{i \to j}}} \right). $ | (4) |
实际中,虽然某些支路的故障传播概率不大,但因其处于故障传播模型结构中较关键的位置,也可能引发高危害的故障传播状态.度量位置重要度的边介数指标一方面反映故障流经频率,一方面体现与模型中其他支路联络关系的密切程度[14],边介数应视为影响故障传播行为的重要模型结构指标.
本文定义组件间故障传播强度I(ei→j)为故障通过有向边ei→j进行传播的强值,该值越大表示故障通过该有向边的传播代价越小且后果越严重,即该边方向为更有利于故障传播的方向.其综合了组件间故障传播概率和边介数两指标量化某有向边对故障传播的贡献作用,作为关键路径识别的依据.
| $ I\left( {{e_{i \to j}}} \right) = \frac{{P\left( {{e_{i \to j}}} \right)}}{{\sum {P\left( {{e_{i \to j}}} \right)} }} + \frac{{L\left( {{e_{i \to j}}} \right)}}{{\sum {L\left( {{e_{i \to j}}} \right)} }}, $ | (5) |
式中L(ei→j)为有向边ei→j的介数值.
4 故障传播机理分析 4.1 故障传播范围界定理论上,模型D1中根源层节点故障可以沿着任意路径一直传至表层节点.实际上,系统安全性要求规定,某条路径的故障传播概率高于阈值10-8时才能进行传播[15].节点vm故障沿着路径k传播至节点vl的概率表示为
| $ {P_k}\left( {{v_m} \to {v_l}} \right) = \prod {P\left( {{e_{i \to j}}} \right)} , $ | (6) |
式中k为路径序号,Pk(vm→vl)表示组成路径k(节点vm至节点vl)相邻节点间故障传播概率乘积值.
因此,应首先基于式(6)界定故障于模型D1的传播范围,再进行关键路径识别.
4.2 关键故障传播路径识别为便于关键故障传播路径识别,可增设虚节点(虚节点即为相关节点的像,在实际系统中并不存在)调整模型结构D1,即去除模型中同层及跨层直接故障传播关系,使得组件间故障传播路径更加直观,便于复杂系统的故障传播过程分析.增设虚节点后的模型为D2.
故障起始于根源层节点,进而分步向上层节点扩散.在界定的故障传播范围内,基于关键路径识别依据I(ei→j),识别模型D2各层级关键节点,这些节点组成的路径则视为系统关键故障传播路径.
5 实例 5.1 数控车床分层故障传播有向图模型构建依据国产某型数控车床故障数据,对逐条故障信息进行故障机理分析,据此构造数控车床故障传播有向图D=(V, E),如图 2所示.

|
1—数控系统;2—进给系统;3—刀架;4—电气系统;5—伺服系统;6—主传动系统;7—液压系统;8—辅助系统;9—基础部件 图 2 数控车床故障传播有向图(D) Figure 2 Failure propagation digraph of CNC Lathe |
其矩阵化表达形式,直接影响矩阵Y=[yij]n×n为
| $ \mathit{\boldsymbol{Y}} = \begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}}\\ {{v_3}}\\ {{v_4}}\\ {{v_5}}\\ {{v_6}}\\ {{v_7}}\\ {{v_8}}\\ {{v_9}} \end{array}\left[ {\begin{array}{*{20}{c}} 0&0&3&0&0&2&0&1&1\\ 0&0&0&0&1&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 1&1&4&0&0&3&1&3&1\\ 0&0&2&0&0&5&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&1&2&0&0&0&0&5&2\\ 0&0&0&0&0&1&0&0&1\\ 0&0&0&0&0&0&0&0&0 \end{array}} \right]. $ |
式中
| $ {y_{ij}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = j;\\ \left\{ \begin{array}{l} 组件\;{v_i}\;故障引起组件\;{v_j}\;发生故障的次数,\\ \left( {i = 1,2, \cdots ,n;j = 1,2, \cdots ,n} \right)\;\;\;i \ne j. \end{array} \right. \end{array} \right. $ |
依据直接影响矩阵Y,具体参照文献[16],分解模型D中各组件节点层级,如表 1所示.
| 表 1 组件节点层级分解表 Table 1 Component node hierarchy decomposition table |
依据表 1,提取骨架矩阵M′为
| $ \mathit{\boldsymbol{M'}} = \begin{array}{*{20}{c}} {{v_3}}\\ {{v_6}}\\ {{v_9}}\\ {{v_5}}\\ {{v_8}}\\ {{v_1}}\\ {{v_2}}\\ {{v_7}}\\ {{v_4}} \end{array}\left[ {\begin{array}{*{20}{c}} 0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0&0&0\\ 1&1&0&0&0&0&0&0&0\\ 0&1&1&0&0&0&0&0&0\\ 1&0&0&0&1&0&0&0&0\\ 0&0&0&1&0&0&0&0&0\\ 0&0&0&0&1&0&1&0&0\\ 0&0&0&0&0&1&0&1&0 \end{array}} \right]. $ |
依据表 1从上到下逐级排列组件节点,依据骨架矩阵M′确定各层级组件节点间连接关系并用有向边表示,据此构建数控车床分层故障传播有向图模型D1,如图 3所示.

|
图 3 数控车床分层故障传播有向图(D1) Figure 3 CNC Lathe hierarchy failure propagation digraph |
数控车床组件节点数n为9,组件间传播故障数为41,系统总故障数为129,因此定义一个维度为9的故障影响度向量R=[R(v1), R(v2), …R(v9)]T,阻尼因子d=41/129≈0.317 8,赋予R1=(1, 1, …, 1)T,设迭代收敛平稳阀值ε=0.000 1.
根据直接影响矩阵Y,构造修正的状态转移概率矩阵Q′为
| $ \mathit{\boldsymbol{Q'}} = \begin{array}{*{20}{c}} {{v_1}}\\ {{v_2}}\\ {{v_3}}\\ {{v_4}}\\ {{v_5}}\\ {{v_6}}\\ {{v_7}}\\ {{v_8}}\\ {{v_9}} \end{array}\left[ {\begin{array}{*{20}{c}} 0&0&0&1&0&0&0&0&0\\ 0&0&0&{\frac{1}{2}}&0&0&{\frac{1}{2}}&0&0\\ {\frac{3}{{11}}}&0&0&{\frac{4}{{11}}}&{\frac{2}{{11}}}&0&{\frac{2}{{11}}}&0&0\\ {\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}&{\frac{1}{9}}\\ 0&1&0&0&0&0&0&0&0\\ {\frac{2}{{11}}}&0&0&{\frac{3}{{11}}}&{\frac{5}{{11}}}&0&0&{\frac{1}{{11}}}&0\\ 0&0&0&1&0&0&0&0&0\\ {\frac{1}{9}}&0&0&{\frac{3}{9}}&0&0&{\frac{5}{9}}&0&0\\ {\frac{1}{5}}&0&0&{\frac{1}{5}}&0&0&{\frac{2}{5}}&{\frac{1}{5}}&0 \end{array}} \right]. $ |
依据式(2),编程计算各组件故障影响度R(vi),如表 2所示.
| 表 2 组件节点故障影响度 Table 2 Component node failure influence degree |
进而根据模型D1和式(3),计算组件间故障影响度R(ei→j),如表 3所示.
| 表 3 组件间故障影响度 Table 3 Failure influence degree between component nodes |
依据各组件故障数据,构建组件故障概率函数Fi(t),并计算系统运行时间为800 h时,各组件的故障概率,整理如表 4所示.
| 表 4 组件节点故障概率 Table 4 Component node failure probability |
依据式(4),结合表 3、表 4,计算组件间故障传播概率P(ei→j),如表 5所示.
| 表 5 800 h组件间故障传播概率 Table 5 Failure propagation probability between component nodes /800 h |
计算模型D1各边介数L(ei→j),如表 6所示.
| 表 6 边介数 Table 6 Edge betweenness |
依据式(5),结合表 5、表 6,计算组件间故障传播强度I(ei→j),如表 7所示.
| 表 7 800 h组件间故障传播强度 Table 7 Failure propagation strength between component nodes /800 h |
依据式(6)界定模型D1的故障传播范围,以根源层节点v4故障沿着路径1传播至表层节点v3为例,P1(v4→v3)=P(e4→1)P(e1→3)=4.104 6E-03.
同理
| $ {P_2}\left( {{v_4} \to {v_3}} \right) = 1.977\;7{\rm{E}} - 05, $ |
| $ {P_3}\left( {{v_4} \to {v_6}} \right) = 1.977\;7{\rm{E}} - 05, $ |
| $ {P_4}\left( {{v_4} \to {v_6}} \right) = 2.417\;5{\rm{E}} - 04, $ |
| $ {P_5}\left( {{v_4} \to {v_6}} \right) = 3.011\;8{\rm{E}} - 04, $ |
| $ {P_6}\left( {{v_4} \to {v_9}} \right) = 2.417\;5{\rm{E}} - 04, $ |
| $ {P_7}\left( {{v_4} \to {v_9}} \right) = 3.011\;8{\rm{E}} - 04, $ |
皆高于阈值10-8.计算结果表明:距离最远的故障表层节点都在根源层节点故障可到达的传播范围内.因此,界定故障能够沿着模型D1中任意路径到达任何节点.
模型D1中存在三处跨层直接故障传播关系,分别为e4→1、e1→3、e7→8,不便于故障传播过程分析.引入虚节点v1′、v3′、v8′从而阻断节点v4和v1,v1和v3,v7和v8的直接联系,得到模型D2,如图 4所示.

|
图 4 增设虚节点的数控车床分层故障传播有向图(D2) Figure 4 CNC Lathe hierarchy failure propagation digraph with virtual nodes |
故障由根源层L5分步向上传播,由图 4可知,一步传播L5→L4有两条支路,根据表 7可知,I(e4→7)=0.254 6>I(e4→1)=0.152 1,因此,故障优先选择路径v4→v7进行传播,定位v7为L4层关键节点.重复此步骤,逐级确定关键节点v2、v5、v3,这些节点组成的路径②则视为运行时间为800 h时系统的关键故障传播路径,对应系统组件为电气→液压→进给→伺服→刀架.关键路径排序为②、③、⑦、⑤、⑥、④、①.在关键路径②和次关键路径③上,故障根源层组件为电气系统,属于动力机构是系统故障源;故障表层组件为刀架和主传动系统,属于执行机构是系统故障多发组件,与数控车床故障数据中二者故障数目较多相符.
要提高系统整体可靠性、安全性,应重点防护关键路径,有针对性地对关键节点进行监测并诊断,及时排除故障隐患,防止故障蔓延.
6 结论1) 基于数控车床组件运行故障信息,应用有向图理论、集成DEMATEL/ISM方法构建了数控车床分层故障传播有向图模型,实现了系统层级分解,即描述了故障的分步扩散结构,同时直观清晰地展示出组件间多层故障传播路径,简化了故障传播分析过程,为关键路径识别奠定基础.
2) 引入PageRank算法评估组件间故障影响度,结合组件节点故障概率,度量组件间故障传播概率;基于组件间故障传播概率和模型结构指标边介数定义故障传播强度表征故障传播行为,值越大表示故障通过某支路的传播代价越小且后果越严重,作为关键路径识别的依据.
3) 在界定的故障传播范围内,基于故障传播强度,结合增设虚节点的系统分层故障传播有向图,模拟故障分步扩散过程,定位系统故障源:电气系统.识别系统关键故障传播路径:电气系统→液压系统→进给系统→伺服系统→刀架,从而实现了数控车床故障传播机理分析,研究结论为故障诊断奠定基础.
| [1] |
WANG Yifeng, CHANG C T. A hierarchical approach to construct Petri nets for modeling the fault propagation mechanisms in sequential operations[J]. Computers & Chemical Engineering, 2003, 27(2): 259-280. DOI:10.1016/S0098-1354(02)00193-X |
| [2] |
PENG Sancheng, WANG Guojun, YU S. Modeling the dynamics of worm propagation using two-dimensional cellular automata in smartphones[J]. Journal of Computer and System Sciences, 2013, 79(5): 586-595. DOI:10.1016/j.jcss.2012.11.007 |
| [3] |
WANG Xiaofan, XU Jian. Cascading failures in coupled map lattices[J]. Physical Review E, 2004, 70(5): 056113. DOI:10.1103/PhysRevE.70.056113 |
| [4] |
BOBBIO A, CODETTA-RAITERI D, MONTANI S, et al. Modeling cascading failure propagation through dynamic bayesian networks[J]. IFAC Proceedings Volumes, 2009, 42(5): 209-214. DOI:10.3182/20090610-3-IT-4004.00041 |
| [5] |
LI Daqing, JIANG Yinan, KANG Rui, et al. Spatial correlation analysis of cascading failures: Congestions and Blackouts[J]. Scientific Reports, 2014, 4(4): 5381. DOI:10.1038/srep05381 |
| [6] |
王广勇, 郭正才, 朱艳飞. 数控机床主轴系统FMECA分析及改进措施[J]. 组合机床与自动化加工技术, 2015(11): 111-113. WANG Guangyong, GUO Zhengcai, ZHU Yanfei. FMECA and improve measurement of spindle system of CNC[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2015(11): 111-113. DOI:10.13462/j.cnki.mmtamt.2015.11.031 |
| [7] |
盛博, 邓超, 熊尧, 等. 基于图论的数控机床故障诊断方法[J]. 计算机集成制造系统, 2015, 21(6): 1559-1570. SHENG Bo, DENG Chao, XIONG Yao, et al. Fault diagnosis for CNC machine tool based on graph theory[J]. Computer Integrated Manufacturing Systems, 2015, 21(6): 1559-1570. DOI:10.13196/j.cims.2015.06.019 |
| [8] |
舒征宇, 邓长虹, 黄文涛, 等. 小世界电力网络故障传播过程与抑制策略[J]. 电网技术, 2013, 37(3): 862-867. SHU Zhengyu, DENG Changhong, HUANG Wentao, et al. Analysis on propagation of cascading failure in small-world power network and its suppressing strategy[J]. Power System Technology, 2013, 37(3): 862-867. DOI:10.13335/j.1000-3673.pst.2013.03.016 |
| [9] |
史浩. 基于网络模型的设备集成系统安全控制方法研究[D]. 北京: 北京交通大学, 2016. SHI Hao. Research on safety and control method for equipment integrated system based on network model[D]. Beijing: Beijing Jiaotong University, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3124729 |
| [10] |
KOKAWA M, MIYAZAKI S, SHINGAI S. Fault location using digraph and inverse direction search with application[J]. Automatica, 1983, 19(6): 729-735. DOI:10.1016/0005-1098(83)90039-0 |
| [11] |
BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Computer Networks and ISDN Systems, 1998, 30(1): 107-117. DOI:10.1016/S0169-7552(98)00110-X |
| [12] |
刘津彤. 基于有向图的数控车床故障传播机理研究[D]. 长春: 吉林大学, 2017. LIU Jintong. Research on failure propagation mechanism of CNC Lathe based on digraph[D]. Changchun: Jilin University, 2017. |
| [13] |
ZHANG Yingzhi, LIU Jintong, SHEN Guixiang, et al. Reliability evaluation of machine center components based on cascading failure analysis[J]. Chinese Journal of Mechanical Engineering, 2017, 30(4): 933-942. DOI:10.1007/s10033-017-0144-y |
| [14] |
孙玺菁, 司守奎. 复杂网络算法与应用[M]. 北京: 国防工业出版社, 2015: 32-34. SUN Xijing, SI Shoukui. Complex network algorithm and application[M]. Beijing: National Defend Industry Press, 2015: 32-34. |
| [15] |
祝庚, 陈毅华, 候家利. K步故障扩散算法的设计与实现[J]. 计算机测量与控制, 2005, 13(8): 784-787. ZHU Geng, CHEN Yihua, HOU Jiali. Design and realization of K-steps fault pervasion algorithm[J]. Computer Measurement & Control, 2005, 13(8): 784-787. DOI:10.16526/j.cnki.11-4762/tp.2005.08.013 |
| [16] |
张英芝, 吴茂坤, 申桂香, 等. 基于DEMATEL/ISM的组合机床故障相关性分析[J]. 工业工程, 2014, 17(3): 92-96, 127. ZHANG Yingzhi, WU Maokun, SHEN Guixiang, et al. An analysis of failure correlation of assemble machine tool based on DEMATEL / ISM[J]. Industrial Engineering Journal, 2014, 17(3): 92-96, 127. DOI:10.3969/j.issn.1007-7375.2014.03.017 |
 2018, Vol. 50
2018, Vol. 50


