2. 国家板带生产先进装备工程技术研究中心(北京科技大学),北京 100083;
3. 江苏帝尔保机械有限公司,扬州 225000
2. National Engineering Research Center of Flat Rolling Equipment(University of Science and Technology Beijing), Beijing 100083, China;
3. Jiangsu Durable Machinery Co., Yangzhou 225000, Jiangsu, China
高强钢在辊弯成型过程中,产生较大弹性回复,即存在回弹问题,已经严重制约其在汽车行业中的应用.很多学者通过建立材料模型和有限元模型来改善回弹预测精度.近年来,国内外学者研究发现,在循环加载卸载实验中,随着塑性应变的增加,高强钢的弹性模量出现逐渐减少趋势,即非线性滞后现象. Morestin等[1]通过单轴循环分析发现,塑性应变仅5%时,弹性模量下降了14%以上. Yoshida等[2]通过循环加载DP590实验与仿真分析发现,当增加预应变时,弹性模量出现迅速下降的趋势,弹性模量下降了20%以上. Cleveland等[3]建立了非线性弹性模量模型,发现在预应变12%下,高强钢弹性模量下降了22%;6022-T铝弹性模量下降了12%. Fei等[4]分析发现TRIP钢的弹性模量下降了12%以上. Abdel-Karim等[5]研究发现:考虑变弹性模量能够提高棘轮效应模拟的精度. Mendiguren等[6]通过非线性加载卸载试验,发现TRIP 700在预应变12%时,弹性模量下降了20%左右. Govik等[7]通过微观有限元研究了DP600非线性变弹性模量问题.高强钢在循环加载-卸载-加载过程中,应力应变也是非线性的,加载曲线路径不再沿原卸载曲线路径,表现出一定的滞后现象[8-9].高强钢弹性模量的降低对准确预测回弹有很大影响作用.考虑变弹性模量时,能够显著改善回弹的预测精度. Yu[10]通过等轴循环加载卸载拉伸试验分析了TRIP600钢非弹性回复机理问题,认为与定弹性模量相比,弦线模量更能准确预测冲压的回弹问题,这一观点在实验中得到了良好的验证. Ghaei等[11-13]利用弦线模量Yochida-Uemori模型描述变弹性模量,结合L-拉弯试验及有限元仿真验证其准确预测回弹优势. Chongthairungruang等[14]通过实验和有限元分析3种材料模型,发现Yochida-Uemori模型能更准确预测高强钢回弹问题,预成型改变了材料的弹性模量,且预成型显著影响回弹量大小,考虑塑性应变引起的变弹性模量模型能更准确预测高强钢的回弹问题. Hassan等[15]利用Yoshida-Uemori模型,提高了冲压预测回弹精度,DP1000预测精度提高了24.5%,DP600预测精度提高了33.3%以上.徐虹等[16]对DP780高强钢进行循环加载卸载试验,研究其变弹性模量变化规律,并建立变弹性模量变化公式,通过冲压验证了其变弹性模量能够较高精度预测回弹问题. Yoshida-Uemori模型能够准确描述复杂的循环加载变弹性模量特性,已经应用到冲压、折弯[4]、拉弯、L弯曲[12]等行业中.辊弯成型是一个渐变的弯曲过程,板带在横向方向上经历弯曲-卸载-再弯曲的渐变成型过程,弹性模量会出现显著变化.变弹性模量变化显著影响辊弯成型回弹预测精度,然而国内外对这一问题还没有展开研究.
本文研究变弹性模量对高强钢辊弯成型回弹预测精度影响,采用拉伸试验和循环加载试验分析DP980变弹性模量问题.通过屈服面法和弹性模量转化面法,建立变弹性模量解析式.在考虑变弹性模量条件下, 分别利用有限元MARC软件仿真预测辊弯成型回弹,对比仿真与试验的回弹结果,发现考虑变弹性模量时能够显著提高连续辊弯成型回弹的预测精度.
1 材料模型 1.1 材料高强钢DP980的材料厚度为1.4 mm,化学成份见表 1.该材料塑性加工性能好,屈服点低,延伸率高而且吸能性好. DP980是由连续的铁素体中环绕分布着岛状马氏体组成,其平均马氏体分数在48%左右.
| 表 1 DP980高强钢的化学组成成份 Table 1 Chemical compositions for DP980 |
用SANS CMT5105(载荷100 kN)电子万能试验机进行拉伸试验,见图 1(a).其拉伸能力100 kN,精度0.002.按照国家GB/T222.1—2010 A50标准,分别取轧制方向、板带横向方向和45°方向拉伸试件,见图 1(b).用非接触式应变传感器来测量试件应变,拉伸速度为2 mm/min.每组拉伸3次并求平均值,DP980材料的机械性能见表 2.

|
(a)拉伸示意(b)3个方向拉伸后试件(c)循环加载-卸载-拉伸试件 图 1 材料性能试验 Figure 1 Material properties testing |
循环加载卸载试验在SANS CMT5105电子万能试验机上进行,拉伸条件同等轴拉伸试验,预应变设置为:0.5%、0.8%、1.0%、2.0%、3.0%、4.0%、5.0%、6.0%、7.0%、8.0%、9.0%和10.0%.循环加载见图 2.

|
图 2 循环加载-卸载-加载路径示意 Figure 2 Description of the loading-unloading-loading cycle |
加载分5步进行:1)加载到预设应变值;2)加载中断;3)持续卸载;4)卸载终止且应力值为零;5)重新加载.
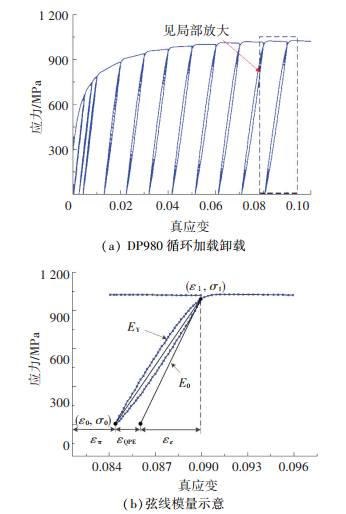
1.4 弦线模量模型DP980循环加载试验结果见图 3(a).从图 3中可以看出,卸载和循环加载的弹性模量是非线性的,重新加载时弹性模量具有迟滞特性,且随着塑性应变的增加,迟滞特性表现越明显. Eu为弦线模量,即开始卸载点与重新加载点连线的斜率.
| $ {E_{\rm{u}}} = \frac{{\left( {{\sigma _1} - {\sigma _0}} \right)}}{{\left( {{\varepsilon _1} - {\varepsilon _0}} \right)}}\left[ {{\rm{MPa}}} \right]. $ |
|
图 3 循环加载卸载试验结果 Figure 3 Results of uniaxial cycle tensile test |
随着塑性应变的增加,弹性模量降低,弦线模量应用到有限元中,即
| $ {E_{{\rm{av}}}} = {E_{\rm{0}}} - \left( {{E_{\rm{0}}} - {E_{\rm{a}}}} \right)\left( {1 - {{\rm{e}}^{ - \xi \bar \varepsilon {\rm{p}}}}} \right). $ | (1) |
式(1)由Yoshida等[2]提出,其中,Eav为辊弯成型中弹性模量的平均值,E0为原始弹性模量,Ea和ξ为材料参数,εp为材料成型过程中塑性应变.
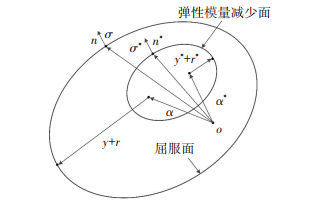
弦线模量随不同加载阶段而变化,初始开始逐渐减少,即斜率逐渐减少.在成型初始状态,弹性模量是连续恒定的.弹性模量减少转化面f*和塑性屈服转化面f的定义见图 4.
| $ {f^ * } = {Ø ^ * }\left( {{\sigma ^ * } - {\alpha ^ * }} \right) - {y^ * } - {r^ * }\left( p \right), $ |
| $ f = Ø \left( {\sigma - \alpha } \right) - y - r\left( p \right). $ |
|
图 4 弹性模量转化面示意 Figure 4 Definition of variables in the transition surface |
式中:σ*、σ为应力张量,α*、α为反应力张量,y*为弹性模量减小转化面内径,y为屈服转化面,r*为弹性模量减少转化面增量,r为塑性转化面增量.
| $ \varepsilon = {\varepsilon _{\rm{p}}} + {\varepsilon _{{\rm{QPE}}}} + {\varepsilon _{\rm{e}}}. $ |
式中:εp为塑性应变,εe为弹性应变,εQPE为准弹塑性应变.在连续辊弯成型过程中,材料成型处于3种状态:弹性阶段,即应力点处于弹性模量减少转换面内;非线性弹性阶段,即应力处于弹性模量转化面与塑性屈服面之间(包括弹性模量减少面之上);塑性阶段,即应力处于屈服面之外(也包含曲面之上),加载方向向外.
弹性阶段是经典的弹性理论,本论文不再介绍.非线性阶段的弹性模量变化,应变与应力的关系为
| $ {\rm{d}}{\sigma ^ * } = \frac{E}{{{E_0}}}{D_0}:{\rm{d}}\varepsilon . $ |
式中:D0为经典的弹性模量,E0为材料的初始弹性模量,可由拉伸试验获得.该阶段变弹性模量为
| $ E = {E_0} - {E_0}\left( {1 - {{\rm{e}}^{ - \xi {\rm{p}}}}} \right)\left[ {1 - {{\rm{e}}^{ - \xi \int {\left\| {{\rm{d}}\varepsilon } \right\|} }}} \right], $ |
| $ {\rm{d}}{\alpha ^ * } = \frac{{{n^ * }:{\rm{d}}{\sigma ^ * }}}{{{n^ * }:\left( {\sigma - {\sigma ^ * }} \right)}}\left( {\sigma - {\sigma ^ * }} \right). $ |
塑性阶段,应力应变的关系为
| $ d{\sigma ^ * } = {D_1}:\left( {{\rm{d}}\varepsilon - {\rm{d}}{\varepsilon ^{\rm{p}}}} \right), $ |
| $ E = {E_0} - {E_0}\left( {1 - {{\rm{e}}^{ - \xi {\rm{p}}}}} \right)\left[ {1 - {{\rm{e}}^{ - \xi \int {\left\| {{\rm{d}}\varepsilon - {\rm{d}}{\varepsilon ^{\rm{p}}}} \right\|} }}} \right], $ |
| $ {\rm{d}}{\alpha ^ * } = \frac{{{n^ * }:{\rm{d}}{\sigma ^ * } - \frac{{\partial {r^ * }}}{{\partial p}}{\rm{d}}p}}{{{n^ * }:\left( {\sigma - {\sigma ^ * }} \right)}}\left( {\sigma - {\sigma ^ * }} \right), $ |
| $ {\rm{d}}{r^ * } = M\left( {N - {r^ * }} \right){\rm{d}}p. $ |
式中:M、N为材料参数,可以通过几次循环加载测得.该材料模型可以通过材料子程序[9],通过应用UMAT和VUMAT应用到MARC中.
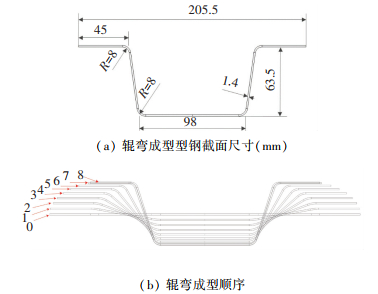
2 辊弯成型有限元模型的建立 2.1 FEA模型建立本论文研究的汽车用薄壁结构件具体尺寸如图 5 (a).利用COPRA专业软件,采用定弧长变半径设计工艺.成型顺序采用下山成型法,如图 5 (b)所示.机架间距450 mm,原始板带长度取1 000 mm,即大于两倍机架间距,保证同时有两组轧辊参与成型.为了更加有利于板带进入,该模型加入了支撑辊.创建的DP980门槛加强件三维模型如图 6所示.
|
图 5 辊弯成型模型设计 Figure 5 The model of design in cold roll forming |

|
图 6 DP980门槛加强件三维模型 Figure 6 The 3D model of Reinforced beam of door DP980 |
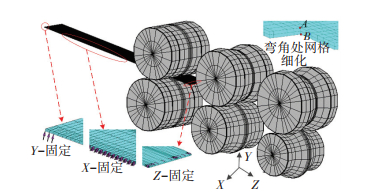
研究发现,壳-实单元能更准确预测回弹现象[17].该单元在厚度方向上有任意积分点,且每个积分点保留了实体单元的力学性能,同时消除了壳单元自锁现象.虽然积分点数对计算精度有一定影响,但以往学者分析发现,7~11积分点就能保证计算精度和效率.所以,本论文选用的壳-实185单元,积分点数选9.相对于板带, 轧辊变形可以忽略,则选择为解析刚体[18].为了提高计算效率,本文采用弯角区域网格细化,其余区域使用较粗的网格的原则,如图 7所示.网格为2层,整个板带的节点为16 698个,单元为10 584个.
|
图 7 有限元仿真模型 Figure 7 Finite element simulation model |
结合试验情况,仿真模型设定为下轴驱动,成型道次为8道次,驱动辊底径每机架递增2 mm,成型速度为20 rad/min,则板带线速度为10.4 mm/s.开始时板带先被拉到第一对轧辊之间,然后,靠板带与轧辊表面之间的摩擦实现向前移动,摩擦系数取0.2.为了保证仿真与试验条件相吻合,施加的约束如图 7所示,对于X约束,所有节点沿中心对称面在X方向进行固定;对于Y约束[19],在中心对称面末端底部最后的3个节点在Y方向固定;对于Z约束,前后两端所有的节点在Z方向固定.在对比不同弹性模量仿真时,单元类型、网格密度、边界条件和初始板带尺寸都要选取一致.
3 门槛加强件辊弯试验试验条件与仿真条件一致,试验机组如图 8(a)所示,精整起到校直板带和消除部分残余应力的作用.为了试验需求,冲孔机没有参与试验,即板带没有预冲孔.而辊弯机组的导向辊防止板带左右偏移,避免板带走偏. 图 8(b)为第7道与第8道成型效果. 图 8(c)为测量成型后角度,与设计对比,可以计算出回弹角度.辊弯成形后的测量位置,处于前后两端300~350 mm,以避免端口张开等其他问题对回弹的影响.测量3次,求平均值即为成型后的角度,以避免操作误差..

|
图 8 辊弯成型试验 Figure 8 Cold roll forming experiment |
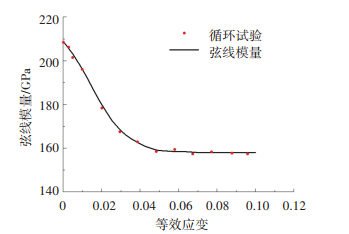
如2.3节描述,通过循环加载-卸载-加载试验,得出DP980不同塑性应变的弹性模量,如图 9所示.由图 9可知,随着塑性应变的增加,弹性模量开始迅速减少,接着缓慢减少,最后,成为一个定值,DP980双相钢在塑性应变10%下弹性模量下降了28%.随着塑性应变的增加,残余应力也在增加,残余应力阻碍材料弹性回复,进而弹性模量下降[20].在塑性应变过程中,微观损伤降低了材料特性,降低了弹性模量[21-22].合金中的孪晶或滞区带也会引起弹性模量变化[23-24].另外,随着塑性应变增加,晶界之间位错堆积与位错重组,是引起弹性模量下降的重要原因之一[25-26].通过微观组织观察,发现位错的密度随着塑性应变的增加,先迅速增高,接着缓慢增高,最后,位错密度处于相对稳定的位置[27].以上是造成弹性模量先急速下降,接着缓慢下降,最后稳定的原因.
|
图 9 不同塑性应变下的弦线模量 Figure 9 Chord modulus evolution at different pre-strains |
根据循环加载-卸载-加载试验结果,DP980门槛加强件在辊弯过程中,弦线弹性模量随塑性应变的变化公式为
| $ {E_{\rm{u}}} = 208\;763 - \left[ {208\;763 - 158\;119} \right]\left[ {1 - {{\rm{e}}^{ - 76.3{{\bar \varepsilon }^{\rm{p}}}}}} \right]. $ | (2) |
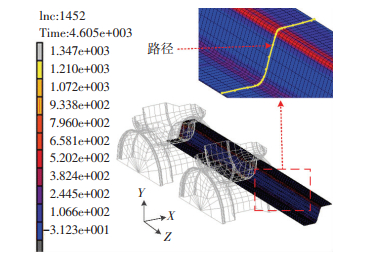
DP980在辊弯成型过程中,在对称面宽度方向上,弯角处发生横向弯曲,主要产生横向应变,尤其弹性应变.当板带轧辊成型后,此时,发生弹性回复,即回弹发生. 图 10为横向应力分布情况.
|
图 10 辊弯成型后横向应力分布与数据分析路径 Figure 10 Distribution of transversal stress in the last channel section after the roll forming process and location of date acquisition |
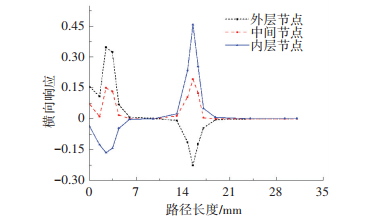
为了便于分析不同弹性模量模型对于应力应变的影响,选取了相同数据提取路径.如图 11所示,辊弯成型后在选取路径应变时,发现最大应变发生在弯曲处,中间层横向应变远小于上下层的横向应变;外层节点弯曲处最大拉应变大于内层节点该弯曲处的压应变,表明在厚度方向上中性层发生轻微的偏移,向压缩节点层偏移.
|
图 11 宽度路径方向横向应变 Figure 11 Transversal strains extracted from the strip path |
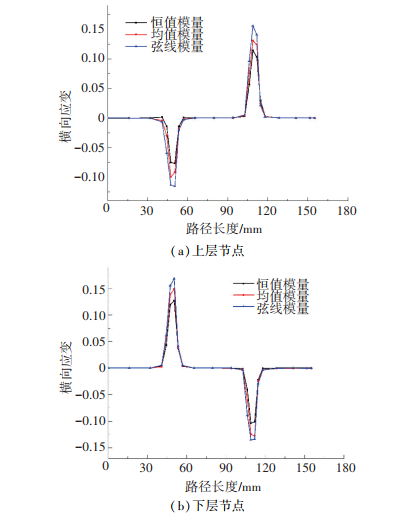
为了对比分析弹性模量模型对辊弯成型回弹精度预测的影响,本论文运用相同的塑性本构模型(均值表 2),分析了不同弹性模量模型(恒值弹性模量、均值弹性模量和弦线弹性模量模型). 图 12为辊弯成型后,横截面方向指定路径(图 10)下,弹性应变分布情况.上层节点弦线模量模型最大横向应变比恒值弹性模量模型应变大约40%,下层节点弦线模量模型最大横向变比恒值模量模型应变大了43%左右,而弹性应变大小决定回弹角度大小.
| 表 2 拉伸试验的DP980机械性能 Table 2 Mechanical properties of DP980 steel sheets |
|
图 12 不同弹性模量宽度路径方向横向应变 Figure 12 Transversal strains extracted from the strip pathbased on different elastic modulus |
在仿真中,恒值模量为209 GPa,均值模量为173 GPa,弦线模量如式(2)所示.不同弹性模量回弹仿真结果与试验对比见表 3, 由表 3可知, 弦线模量模型能更准确预测回弹.分析仿真结果与试验结果发现,回弹角都小于试验值.考虑变弹性模量的DP980门槛加强件回弹角比恒值模量回弹预测精度提高约24%,回弹角精度提高了23%以上;考虑弦线模量的DP980门槛加强件,回弹角比均值弹性模量法提高了8%,回弹角精度提高了10%.同时,说明随着弹性模量的增加回弹角度大小亦增加.
| 表 3 不同弹性模量模型回弹与试验对比 Table 3 Comparison of the springback between experiment and simlations |
即使考虑变弹性模量,仿真回弹精度与试验回弹精度相比,仍有15%差距.这与初始板带在辊弯之前,DP980材料内部有一定的残余应力有关[28-30],仿真模型中未考虑残余应力对回弹有一定影响[31].本模型只考虑变弹性模量问题,而未考虑材料在加工过程中的包辛格效应、瞬态力学行为、永久软化行为、硬化停止行为和材料各项异性等性质[32],而考虑更为复杂的材料模型,有助于进一步改善仿真精度.
仿真回弹精度与试验的差异,可能由成型参数造成[33],如:机架间距、成型速度、摩擦、成型策略、辊缝间距、角度分配等.几何参数如腹板宽度、翼变宽度、型钢高度、板带厚度和弯曲半径等也是造成仿真回弹角度低于试验角度的原因.另外,在试验过程中,设备有一定的变形,尤其轴的刚度,在辊弯成型中,轴可能发生挠曲变形,增加了辊缝间距,进而增加回弹角度.下一步我们的工作重点是,利用变弹性模量分析成型参数及几何参数对回弹的影响.
5 结论1) 循环加载-卸载-加载试验发现, 随着塑性应变的增加,DP980高强钢弹性模量开始迅速减少,接着缓慢减少,最后成为一个恒定值.
2) 在塑性应变10%时,DP980高强钢弹性模量下降25%以上.
3) 建立了弦线准弹塑性模量模型,并用塑性屈服面法和弹性模量减少转化面法解释变弹性模量产生过程.
4) 在高强钢辊弯成型回弹预测时,有必要考虑变弹性模量问题.相对恒值模量模型,考虑变弹性模量模型明显提高了高强钢辊弯成型回弹预测精度,为实现高强钢回弹补偿奠定了良好基础.
| [1] |
MORESTIN F, BOIVIN M. On the necessity of taking into account the variation in the Young modulus with plastic strain in elastic-plastic software[J]. Nuclear Engineering and Design, 1996, 162(1): 107-116. DOI:10.1016/0029-5493(95)01123-4 |
| [2] |
YOSHIDA F, UEMORI T, FUJIWARA K. Elastic-plastic behavior of steel sheets under in-plane cyclic tension-compression at large strain[J]. International Journal of Plasticity, 2002, 18(5/6): 633-659. DOI:10.1016/S0749-6419(01)00049-3 |
| [3] |
CLEVELAND R M, GHOSH A K. Inelastic effects on springback in metals[J]. International Journal of Plasticity, 2002, 18(5/6): 769-785. DOI:10.1016/S0749-6419(01)00054-7 |
| [4] |
FEI D, HODGSON P. Experimental and numerical studies of springback in air v-bending process for cold rolled TRIP steels[J]. Nuclear Engineering and Design, 2006, 236(18): 1847-1851. DOI:10.1016/j.nucengdes.2006.01.016 |
| [5] |
ABDEL-KARIM M. Effect of elastic modulus variation during plastic deformation on uniaxial and multiaxial ratchetting simulations[J]. European Journal of Mechanics-A/Solids, 2011, 30(1): 11-21. DOI:10.1016/j.euromechsol.2010.08.002 |
| [6] |
MENDIGUREN J, CORTÉS F, GÓMEZ X, et al. Elastic behaviour characterisation of TRIP 700 steel by means of loading-unloading tests[J]. Materials Science and Engineering A, 2015, 634: 147-152. DOI:10.1016/j.msea.2015.03.050 |
| [7] |
GOVIK A, RENTMEESTER R, NILSSON L. A study of the unloading behaviour of dual phase steel[J]. Materials Science and Engineering A, 2014, 602: 119-126. DOI:10.1016/j.msea.2014.02.069 |
| [8] |
KIM H, KIM C, BARLAT F, et al. Nonlinear elastic behaviors of low and high strength steels in unloading and reloading[J]. Materials Science and Engineering A, 2013, 562: 161-171. DOI:10.1016/j.msea.2012.11.020 |
| [9] |
SUN L, WAGONER R H. Complex unloading behavior: Nature of the deformation and its consistent constitutive representation[J]. International Journal of Plasticity, 2011, 27(7): 1126-1144. DOI:10.1016/j.ijplas.2010.12.003 |
| [10] |
YU Haiyan. Variation of elastic modulus during plastic deformation and its influence on springback[J]. Materials & Design, 2009, 30(3): 846-850. DOI:10.1016/j.matdes.2008.05.064 |
| [11] |
GHAEI A, GREEN D E. Numerical implementation of Yoshida-Uemori two-surface plasticity model using a fully implicit integration scheme[J]. Computational Materials Science, 2010, 48(1): 195-205. DOI:10.1016/j.commatsci.2009.12.028 |
| [12] |
GHAEI A. Numerical simulation of springback using an extended return mapping algorithm considering strain dependency of elastic modulus[J]. International Journal of Mechanical Sciences, 2012, 65(1): 38-47. DOI:10.1016/j.ijmecsci.2012.09.002 |
| [13] |
GHAEI A, GREEN D E, TAHERIZADEH A. Semi-implicit numerical integration of Yoshida?Uemori two-surface plasticity model[J]. International Journal of Mechanical Sciences, 2010, 52(4): 531-540. DOI:10.1016/j.ijmecsci.2009.11.018 |
| [14] |
CHONGTHAIRUNGRUANG B, UTHAISANGSUK V, SURANUNTCHAI S, et al. Experimental and numerical investigation of springback effect for advanced high strength dual phase steel[J]. Materials & Design, 2012, 39: 318-328. DOI:10.1016/j.matdes.2012.02.055 |
| [15] |
HASSAN H U, FAWAD M, ALPER G, et al. Springback prediction and reduction in deep drawing under influence of unloading modulus degradation[J]. International Journal of Material Forming, 2016, 9(5): 619-633. DOI:10.1007/s12289-015-1248-5 |
| [16] |
徐虹, 刘亚楠, 于婷, 等. 双相钢DP780在循环加载-卸载过程中的非弹性回复行为及其微观机理[J]. 吉林大学学报(工学版), 2017, 47(1): 191-198. XU Hong, LIU Yanan, YU Ting, et al. Inelastic recovery behavior and microscopic mechanism of high strength DP780 steel during cycle loading-unloading[J]. Journal of Jilin University, 2017, 47(1): 191-198. |
| [17] |
ALVESDESOUSA R, YOON J, CARDOSO R, et al. On the use of a reduced enhanced solid-shell (RESS) element for sheet forming simulations[J]. International Journal of Plasticity, 2007, 23(3): 490-515. DOI:10.1016/j.ijplas.2006.06.004 |
| [18] |
韩飞, 朱德鹏. 辊弯成形中成形力的理论分析和有限元仿真[J]. 锻压技术, 2016(12): 150-155. HAN Fei, ZHU Depeng. Theoretical analysis and numerical simulation on forming force in rolling[J]. Forging & Stamping Technology, 2016(12): 150-155. DOI:10.13330/j.issn.1000-3940.2016.12.026 |
| [19] |
ABEYRATHNA B, ROLFE B, HODGSON P, et al. A first step towards a simple in-line shape compensation routine for the roll forming of high strength steel[J]. International Journal of Material Forming, 2016, 9(3): 423-434. DOI:10.1007/s12289-015-1238-7 |
| [20] |
HILL R. The mathematical theory of plasticity[M]. Oxford: Clarendon Press, 1950.
|
| [21] |
YEH H, CHENG J. NDE of metal damage: ultrasonics with a damage mechanics model[J]. International Journal of Solids and Structures, 2003, 40(26): 7285-7298. DOI:10.1016/j.ijsolstr.2003.08.015 |
| [22] |
HALILOVI M, VRH M, TOK B. Prediction of elastic strain recovery of a formed steel sheet considering stiffness degradation[J]. Meccanica, 2009, 44(3): 321-338. DOI:10.1007/s11012-008-9169-8 |
| [23] |
ZHOU A G, BARSOUM M W. Kinking nonlinear elasticity and the deformation of magnesium[J]. Metallurgical and Materials Transactions A, 2009, 40(7): 1741-1756. DOI:10.1007/s11661-009-9845-x |
| [24] |
CÁCERES C H, SUMITOMO T, VEIDT M. Pseudoelastic behaviour of cast magnesium AZ91 alloy under cyclic loading-unloading[J]. Acta Materialia, 2003, 51(20): 6211-6218. DOI:10.1016/S1359-6454(03)00444-0 |
| [25] |
MENDIGUREN J, CORTÉS F, GÓMEZ X, et al. Elastic behaviour characterisation of TRIP 700 steel by means of loading-unloading tests[J]. Materials Science and Engineering A, 2015, 634: 147-152. DOI:10.1016/j.msea.2015.03.050 |
| [26] |
PÉREZ R, BENITO J A, PRADO J M. Study of the inelastic response of TRIP steels after plastic deformation[J]. ISIJ International, 2005, 45(12): 1925-1933. DOI:10.2355/isijinternational.45.1925 |
| [27] |
YANG M, AKIYAMA Y, SASAKI T. Evaluation of change in material properties due to plastic deformation[J]. Journal of Materials Processing Technology, 2004, 151(1/2/3): 232-236. DOI:10.1016/j.jmatprotec.2004.04.114 |
| [28] |
曹建国, 唐慧, 杨光辉, 等. 有高温相变的电工钢热轧起浪的有限元分析[J]. 哈尔滨工业大学学报, 2016, 48(1): 146-151. CAO Jianguo, TANG Hui, YANG Guanghui, et al. Finite element analysis of edge wave for non-oriented electrical strip with high temperature phase transition[J]. Journal of Harbin institute of technology, 2016, 48(1): 146-151. DOI:10.11918/j.issn.0367-6234.2016.01.022 |
| [29] |
彭雪锋, 韩静涛, 刘靖, 等. 感应回火对冷成形高强度钢方管力学特性的影响[J]. 上海交通大学学报, 2017, 51(4): 438-443. PENG Xuefeng, HAN Jingtao, LIU Jing, et al. Effect of induction tempering om mechanical properties of cold-formed high strength steel square tube[J]. Journal of Shanghai Jiaotong University, 2017, 51(4): 438-443. DOI:10.16183/j.cnki.jsjtu.2017.04.009 |
| [30] |
彭雪锋, 韩静涛, 晏培杰, 等. 热成形温度对高强钢方管组织及性能的影响[J]. 工程科学学报, 2016, 38(6): 820-826. PENG Xuefeng, HAN Jingtao, YAN Peijie, et al. Effect of hot forming temperature on the microstructure and mechanical properties of high strength square tubes[J]. Chinese Journal of Engineering, 2016, 38(6): 820-826. DOI:10.13374/j.issn2095-9389.2016.06.011 |
| [31] |
ABVABI A, ROLFE B, HODGSON P D, et al. The influence of residual stress on a roll forming process[J]. International Journal of Mechanical Sciences, 2015, 101-102: 124-136. DOI:10.1016/j.ijmecsci.2015.08.004 |
| [32] |
ZHAN Mei, YANG He, GUO Jing, et al. Review on hot spinning for difficult-to-deform lightweight metals[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(6): 1732-1743. DOI:10.1016/S1003-6326(15)63778-5 |
| [33] |
曹建国, 王乐, 刘江, 等. 基于过弯缺陷控制的异型管辊弯成型过程有限元仿真[J]. 中南大学学报(自然科学版), 2017, 48(9): 2345-2351. CAO Jianguo, WANG Le, LIU Jiang, et al. Finite element simulation of roll forming process based on over-bend defect control of shaped tube[J]. Journal of Central South University (Science and Technology), 2017, 48(9): 58-63. DOI:10.11817/j.issn.2345-2351.2017.09 |
 2018, Vol. 50
2018, Vol. 50


