星形轮系相比平行轴齿轮传动,具有体积小、重量轻、承载能力大等优点,广泛应用于汽车、船舶、航空航天等领域,但由于不可避免的制造和安装误差、轮齿弹性变形等,载荷无法实现在星型轮系各路功率分流间均匀分配,从而降低系统的承载能力,还会引起部分构件的过载和振动噪声问题,因此在传动设计中必须考虑到星轮间载荷分布的不均匀性.
从20世纪80年代至今,关于功率分流系统的均载特性,国内外学者就进行了多方面的研究. Ma等[1]研究了行星轮系动态载荷对系统均载特性的影响. Kahraman[2]考虑了齿轮安装制造误差对系统均载特性的影响,并计算了均载系数. Bode、Singh等[3-4]采用有限元接触模型研究了行星架和齿轮制造误差与静态均载系数的关系.袁擎宇等[5]从静力学的角度,运用当量啮合误差原理和浮动构件的平衡关系分析了两级星型齿轮传动静力学均载特性.朱才朝等[6-8]研究了柔性销对均载特性的影响.杜进辅等[9-11]基于集中参数模型和变形协调条件分析了多分流系统均载机理.任菲等[12]从动力学的角度研究了制造误差对人字齿行星轮系动态均载特性的影响.以上对功率分流均载特性的研究大体上分为三类:基于静力学平衡研究系统均载,该方法忽略了系统惯性载荷和动态激励;基于集中参数模型的动态均载特性,该方法忽略掉齿轮轴段自身的柔性[13];基于大型有限元软件的仿真结果分析均载特性,该方法往往存在计算量大、前处理困难等问题.
本文考虑时变啮合刚度、啮合误差、轴段结构柔性的影响,建立柔性销轴式人字齿星型轮系的动力学数学模型.基于动力学响应分析了误差激励、不同柔性销轴结构以及工况参数对系统均载性能的影响规律,为GTF人字齿星型轮系的均载系数确定,误差控制、加工、装配以及柔性销结构设计提供理论依据.
1 柔性销轴式GTF星型轮系传动原理为了降低GTF发动机风扇叶尖切线速度,增大发动机的涵道比,在涡扇发动机的低压压气机和风扇之间增加一个星型齿轮减速器. 图 1中显示了某小功率GTF发动机星型轮系的结构和传动原理,其中图 1(a)为实物模型,图 1(b)为传动简图,各构件参数取不同的下标:内齿圈r,太阳轮s,星轮Pm (m为星轮数,m=1,2,3),输入扭矩Tin,输出扭矩Tout.本星型轮系的星轮采用柔性销支撑的形式,功率经过太阳轮输入,分流到各个星轮,最后汇聚到内齿轮上,并采用人字齿轮传动以消除轴向力,系统中各齿轮参数见表 1.

|
图 1 GTF风扇发动机星型轮系 Figure 1 Star gear transmission system of GTF engine |
| 表 1 星型轮系齿轮参数 Table 1 Gear parameters of star gear transmission system |
柔性销轴最早是在1960年左右,英国发明家Hicks[14]发明的,相比于传统的固定销轴,柔性销轴受载后产生“S”型变形,可以保证各齿轮轴线平行,提高单位齿宽承载能力.此外由于柔性销的刚性较小,有利于各星轮的浮动,还可以避免瞬间载荷过大对系统的冲击,增加系统的承受冲击载荷的能力,有利于改善整个传动链结构件的使用寿命. GTF星型轮系采用Hick柔性销支撑的形式,本文在该销轴的基础上并参考文献[6]建立了其余3种不同结构的星轮悬臂销轴,4种销轴均使用合金结构钢40CrMoV12,该材料的屈服极限为595~715 MPa,各销轴的结构和尺寸如图 2所示.

|
图 2 不同悬臂销轴几何模型 Figure 2 Geometrical model for different cantilever pins |
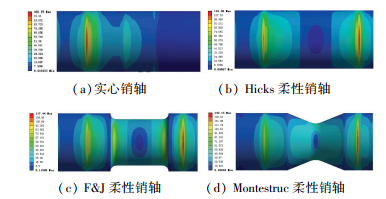
图 2(a)为固定销轴形式,图 2(b)为Hicks柔性销,图 2(c)为2006年Fox和Jallat[15]在Hicks柔性销的基础上改进而来,图 2(d)为2011年Montestruc[6]进一步改进的柔性销. 4种销轴在额定载荷下的应力云图如图 3所示,由图 3可知Montestruc柔性销轴的应力最大,最大应力为142.15 Mpa,远小于所用材料的屈服极限,不会发生屈服破坏,因此本文所建立的销轴模型强度上是足够的.
|
图 3 销轴应力云图 Figure 3 Stress nephogram of the pins |
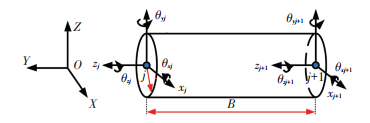
本文采用修正的Euler-Bernouli梁单元[16]建立轴段的动力学方程,如图 4所示,梁单元在单元局部坐标系(OXYZ)下的广义坐标为
| $ {\mathit{\boldsymbol{X}}_J} = {\left\{ {{\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{y}}_j},{\mathit{\boldsymbol{z}}_j},{\theta _{{x_j}}},{\theta _{{y_j}}},{\theta _{{z_j}}},{\mathit{\boldsymbol{x}}_{j + 1}},{\mathit{\boldsymbol{y}}_{j + 1}},{\mathit{\boldsymbol{z}}_{j + 1}},{\theta _{{x_{j + 1}}}},{\theta _{{y_{j + 1}}}},{\theta _{{z_{j + 1}}}}} \right\}^{\rm{T}}}. $ |
|
图 4 Euler-Bernouli梁单元 Figure 4 Euler-Bernouli beam element |
在外载荷下梁单元的动力学微分方程为
| $ {\mathit{\boldsymbol{M}}_J}{{\mathit{\boldsymbol{\ddot X}}}_J} + {\mathit{\boldsymbol{C}}_J}{{\mathit{\boldsymbol{\dot X}}}_J} + {\mathit{\boldsymbol{K}}_J}{\mathit{\boldsymbol{X}}_J} = {\mathit{\boldsymbol{F}}_J}, $ |
式中MJ、KJ、CJ、FJ为第J个梁单元在局部坐标系下的质量、刚度、阻尼和负载矩阵[17].
考虑到在空间梁单元系统中单元的局部坐标系方向各异,在组建轴系单元的总体矩阵时,单元的特性矩阵需要通过空间坐标变换,在总体坐标系下对各轴系单元参数进行描述.
局部坐标系下第J个梁单元节点的位移与在总体坐标系下单元节点位移的关系可以写成
| $ \begin{array}{*{20}{c}} {{{\left\{ {{{x'}_i},{{y'}_i},{{z'}_i},{{\theta '}_{{x_i}}},{{\theta '}_{{y_i}}},{{\theta '}_{{z_i}}},{{x'}_j},{{y'}_j},{{z'}_j},{{\theta '}_{{x_j}}},{{\theta '}_{{y_j}}},{{\theta '}_{{z_j}}}} \right\}}^{\rm{T}}} = }\\ {\mathit{\boldsymbol{R}}{{\left\{ {{x_i},{y_i},{z_i},{\theta _{{x_i}}},{\theta _{{y_i}}},{\theta _{{z_i}}},{x_j},{y_j},{z_j},{\theta _{{x_j}}},{\theta _{{y_j}}},{\theta _{{z_j}}}} \right\}}^{\rm{T}}}.} \end{array} $ | (1) |
式中:R=diag[T; T; T; T]为坐标变换矩阵,T=TγTβTα,α、β、γ为绕着总体坐标系X、Y、Z坐标轴旋转角.
| $ {\mathit{\boldsymbol{T}}_\alpha } = \left[ {\begin{array}{*{20}{c}} {\cos \alpha }&0&{\sin \alpha }\\ 0&1&0\\ { - \sin \alpha }&0&{\cos \alpha } \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{T}}_\beta } = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\sin \beta }&0\\ { - \sin \beta }&{\cos \beta }&0\\ 0&0&1 \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{T}}_\gamma } = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&{\cos \gamma }&{\sin \gamma }\\ 0&{ - \sin \gamma }&{\cos \gamma } \end{array}} \right]. $ |
将坐标变换矩阵代入到式(1)中,可得到第J个梁单元节点在总体坐标系下的单元刚度矩阵和质量矩阵:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_{J'}} = {\mathit{\boldsymbol{R}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_J}\mathit{\boldsymbol{R}},\\ {\mathit{\boldsymbol{M}}_{J'}} = {\mathit{\boldsymbol{R}}^{\rm{T}}}{\mathit{\boldsymbol{M}}_J}\mathit{\boldsymbol{R}}. \end{array} \right. $ | (2) |
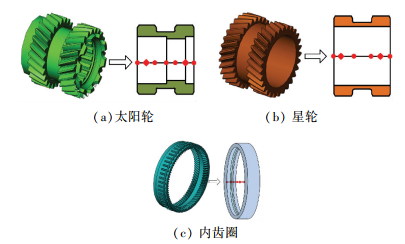
GTF星型轮系动力学建模中,在保证实际模型与理论模型的几何参数和动力学属性相似前提下,将太阳轮轴、星轮轴、齿圈、输出轴等构件进行简化.其等效原则为:在轴段截面突变处、轴承支撑处、齿轮啮合点、功率点等地方划分梁单元的节点[18],系统各齿轮轴等效为梁单元的过程如图 5所示.
|
图 5 齿轮轴等效 Figure 5 Equivalence of the gear shaft |
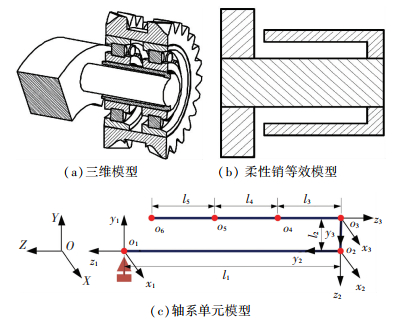
对于柔性销轴,由于其存在空间梁单元结构,其等效较为复杂,以Hicks柔性销为例说明其等效过程,其余柔性销的等效类似,如图 6所示. 图 6中:OXYZ为Hicks柔性销轴单元的总体坐标系; O1、O2、O3、O4、O5、O6为所划分的节点,其中O1为固定支撑点,O4、O5为星轮轴承支撑点,O1O2为轴段单元1,O2O3为轴段单元2,O3O4、O4O5、O5O6为轴段单元3、4、5.分别在O1、O2、O3节点处建立各自的单元局部坐标系,利用式(2)进行坐标变换直接写出在总体坐标系下的各自单元特性矩阵:
| $ {\mathit{\boldsymbol{K}}_1} = {\mathit{\boldsymbol{K}}_J},{\mathit{\boldsymbol{M}}_1} = {\mathit{\boldsymbol{M}}_J}, $ |
| $ {\mathit{\boldsymbol{K}}_2} = \mathit{\boldsymbol{R}}_2^{\rm{T}}{\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{R}}_2},{\mathit{\boldsymbol{M}}_2} = \mathit{\boldsymbol{R}}_2^{\rm{T}}{\mathit{\boldsymbol{K}}_2}{\mathit{\boldsymbol{R}}_2}, $ |
| $ {\mathit{\boldsymbol{R}}_2} = {\rm{diag}}\left[ {{\mathit{\boldsymbol{T}}_2},{\mathit{\boldsymbol{T}}_2},{\mathit{\boldsymbol{T}}_2},{\mathit{\boldsymbol{T}}_2}} \right],{\mathit{\boldsymbol{T}}_2} = {\mathit{\boldsymbol{T}}_{\gamma = 0}}{\mathit{\boldsymbol{T}}_{\beta = 0}}{\mathit{\boldsymbol{T}}_{\alpha = {\rm{ \mathsf{ π} }}/2}}, $ |
| $ {\mathit{\boldsymbol{K}}_3},{\mathit{\boldsymbol{K}}_4},{\mathit{\boldsymbol{K}}_5} = \mathit{\boldsymbol{R}}_3^{\rm{T}}{\mathit{\boldsymbol{K}}_3}{\mathit{\boldsymbol{R}}_3},{\mathit{\boldsymbol{M}}_3},{\mathit{\boldsymbol{M}}_4},{\mathit{\boldsymbol{M}}_5} = \mathit{\boldsymbol{R}}_3^{\rm{T}}{\mathit{\boldsymbol{M}}_3}{\mathit{\boldsymbol{R}}_3}, $ |
| $ {\mathit{\boldsymbol{R}}_3} = {\rm{diag}}\left[ {{\mathit{\boldsymbol{T}}_3},{\mathit{\boldsymbol{T}}_3},{\mathit{\boldsymbol{T}}_3},{\mathit{\boldsymbol{T}}_3}} \right],{\mathit{\boldsymbol{T}}_3} = {\mathit{\boldsymbol{T}}_{\gamma = 0}}{\mathit{\boldsymbol{T}}_{\beta = 0}}{\mathit{\boldsymbol{T}}_{\alpha = {\rm{ \mathsf{ π} }}}}. $ |
|
图 6 Hicks柔性销轴系单元等效 Figure 6 Shafting element equivalence for the Hicks flexible pin |
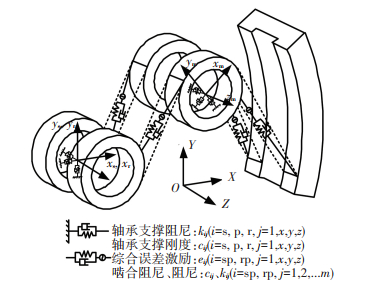
动力学建模中考虑的因素有:各齿轮横向振动、轴向扭转及摆动、轮齿啮合误差以及时变啮合刚度,人字齿星型轮系等效力学模型如图 7所示. 图 7中OXYZ为全局坐标系,oxyz为各齿轮轴的坐标系,其中星轮坐标系以太阳轮和各个星轮的连心线作为x轴.
|
图 7 人字齿星型轮系等效力学模型 Figure 7 Equivalent mechanical model for herringbone star gear transmission system |
将GTF人字齿星型轮系的各个构件看作质量弹性体,轴承支承部位、啮合副的弹性变形以及运动阻尼用等效的弹簧刚度和阻尼来表示,其中各齿轮的轴承支撑刚度和阻尼用符号表示为kij、cij(i=s、p、r;j=x、y、z),内外啮合齿轮副之间的时变啮合刚度、啮合阻尼、误差用符号表示为kij、cij、eij (i=sp、rp; j=1、2、3),左右齿轮位移的自由度表示为xij, yij, zij, θxij, θyij, θzij, (i=s、p、r,j=L、R).
动力学模型中各齿轮的振动位移(包括平动、扭转、摆动位移)均会在轮齿啮合副的啮合线方向产生等效位移,由于人字齿左右两侧结构对称,因此以左侧为例推导各齿轮轴单元的耦合关系.
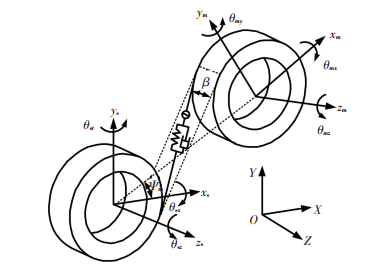
图 8为星型轮系人字齿左侧外啮合齿轮副的动力学模型,图 8中太阳轮和星轮的基圆半径为rs、rm,太阳轮的压力角为αs,螺旋角为β,第m个星轮相位角为ψm,定义外啮合的啮合角为ψsm=ψm-αs,齿轮在啮合线方向的相对位移为δ,太阳轮与第m个星轮的位移向量可以表示为
| $ {\mathit{\boldsymbol{q}}_{{\rm{s}}m}} = {\left[ {{x_{\rm{s}}},{y_{\rm{s}}},{z_{\rm{s}}},{\theta _{{\rm{s}}x}},{\theta _{{\rm{s}}y}},{\theta _{{\rm{s}}z}},{x_m},{y_m},{z_m},{\theta _{mx}},{\theta _{my}},{\theta _{mz}}} \right]^{\rm{T}}}. $ |
|
图 8 外啮合齿轮副动力学模型 Figure 8 Dynamic model of external gearing pair |
取啮合线由太阳轮指向星轮为正方向,啮合线方向的相对位移为δsmL= VsmLqsmL+esm(t),其中
| $ \begin{array}{l} \mathit{\boldsymbol{V}}_{{\rm{s}}m}^{\rm{L}} = \left[ { - \sin {\psi _{{\rm{s}}m}}\mathit{cos}\beta ,\cos {\psi _{{\rm{s}}m}}\cos \beta ,\sin \beta ,} \right.\\ \;\;\;\;\;\;\;\;{r_{\rm{s}}}\sin {\psi _{{\rm{s}}m}}\sin \beta , - {r_{\rm{s}}}\cos {\psi _{{\rm{s}}m}}\sin \beta ,{r_{\rm{s}}}\cos \beta ,\\ \;\;\;\;\;\;\;\;\sin {\psi _{{\rm{s}}m}}\cos \beta , - \cos {\psi _{{\rm{s}}m}}\cos \beta , - \sin \beta ,\\ \;\;\;\;\;\;\;\;\left. {{r_m}\sin {\psi _{{\rm{s}}m}}\sin \beta , - {r_m}\cos {\psi _{{\rm{s}}m}}\sin \beta ,{r_m}\cos \beta } \right]. \end{array} $ |
人字齿左侧内啮合齿轮副啮合向量同外啮合的推导方式一样,令ψrm=ψm+αr,其表达式为
| $ \begin{array}{l} \mathit{\boldsymbol{V}}_{{\rm{r}}m}^{\rm{L}} = \left[ {\sin {\psi _{{\rm{r}}m}}\cos \beta , - \cos {\psi _{{\rm{r}}m}}\cos \beta ,\sin \beta ,} \right.\\ \;\;\;\;\;\;\;\;{r_m}\sin {\psi _{{\rm{r}}m}}\sin \beta , - {r_m}\cos {\psi _{{\rm{r}}m}}\sin \beta , - {r_m}\cos \beta ,\\ \;\;\;\;\;\;\;\; - \sin {\psi _{{\rm{r}}m}}\cos \beta ,\cos {\psi _{{\rm{r}}m}}\cos \beta , - \sin \beta ,\\ \;\;\;\;\;\;\;\;\left. { - {r_{\rm{r}}}\sin {\psi _{{\rm{r}}m}}\sin \beta ,{r_{\rm{r}}}\cos {\psi _{{\rm{r}}m}}\sin \beta ,{r_{\rm{r}}}\cos \beta } \right]. \end{array} $ |
根据系统的离散化程度,将系统划分为多个轴系单元,其中销轴和各个星轮之间通过轴承连接单元进行耦合,齿轮之间通过啮合单元耦合,最后将各个轴系单元有序地连接起来[13],形成GTF星型轮系整体节点有限元模型.以Hicks柔性销轴式齿轮系统为例,节点有限元模型如图 9所示,其他销轴结构支撑下的节点有限元模型与之类似,不再赘诉,图 9中OXYZ为系统的总体坐标系,系统共75个节点、450个自由度.

|
图 9 GTF人字齿星型轮系整体节点有限元模型 Figure 9 Overall node finite element model of herringbone star gear transmission system for GTF engine |
将轴系单元的质量、阻尼、刚度、负载矩阵,按照有限单元法[17]的规则联立并组装形成系统的整体动力学方程为
| $ {\mathit{\boldsymbol{M}}_{\rm{T}}}{{\mathit{\boldsymbol{\ddot X}}}_{\rm{T}}} + {\mathit{\boldsymbol{C}}_{\rm{T}}}{{\mathit{\boldsymbol{\dot X}}}_{\rm{T}}} + {\mathit{\boldsymbol{K}}_{\rm{T}}}{\mathit{\boldsymbol{X}}_{\rm{T}}} = {\mathit{\boldsymbol{F}}_{\rm{T}}}. $ |
式中:MT、KT、CT为系统总体质量、阻尼和刚度矩阵,XT为系统轴系单元节点的位移向量,FT={F1, F2, …, Fn}T为系统外部激振力.
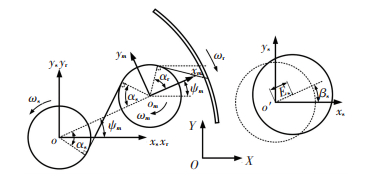
3 系统动态激励分析 3.1 当量啮合误差星型轮系的齿轮误差较为复杂,本文按照文献[9-11]主要考虑齿轮安装误差和制造误差引起的当量啮合误差.齿轮制造误差指齿轮加工制造所产生的几何中心与实际回转中心的偏差,安装误差指构件安装之后实际回转轴线与理论回转轴线的偏差,齿轮的误差示意如图 10所示.
|
图 10 制造误差和安装误差示意图 Figure 10 Diagram of the manufacturing and assembling error |
取太阳轮转向逆时针为角位移正方向,取啮合误差靠近齿向方向为当量啮合误差的正向.齿轮角速度为ω,制造误差、安装误差的幅值为E、A,初始相位角为β、γ,则各齿轮的误差引起的当量啮合误差公式如下:
1) 外啮合各齿轮误差所引起当量啮合误差为
| $ e{E_{{\rm{s}}m}} = {E_{\rm{s}}}\sin \left( {{\omega _{\rm{s}}}t + {\beta _{\rm{s}}} + {\alpha _{\rm{s}}} - {\psi _m}} \right), $ |
| $ e{A_{{\rm{s}}m}} = {A_{\rm{s}}}\sin \left( {{\gamma _{\rm{s}}} + {\alpha _{\rm{s}}} - {\psi _m}} \right), $ |
| $ e{E_{{\rm{ps}}m}} = {E_{\rm{p}}}\sin \left( { - {\omega _m}t + {\beta _m} + {\alpha _{\rm{s}}}} \right), $ |
| $ e{A_{{\rm{ps}}m}} = {A_{\rm{p}}}\sin \left( {{\gamma _m} + {\alpha _{\rm{s}}}} \right). $ |
2) 内啮合各齿轮误差所引起当量啮合误差为
| $ e{E_{{\rm{r}}m}} = {E_{\rm{r}}} \times \sin \left( { - {\omega _{\rm{r}}}t - {\beta _{\rm{r}}} + {\alpha _{\rm{r}}} + {\psi _m}} \right), $ |
| $ e{A_{{\rm{r}}m}} = {A_{\rm{r}}}\sin \left( { - {\gamma _{\rm{r}}} + {\alpha _{\rm{r}}} + {\psi _m}} \right), $ |
| $ e{E_{{\rm{pr}}m}} = {E_{\rm{p}}}\sin \left( { - {\omega _m}t - {\beta _m} + {\alpha _{\rm{r}}}} \right), $ |
| $ e{A_{{\rm{pr}}m}} = {A_{\rm{p}}}\sin \left( { - {\gamma _m} + {\alpha _{\rm{r}}}} \right). $ |
3) 考虑各种误差之后的综合外内啮合误差为
| $ {e_{{\rm{sp}}m}} = e{E_{{\rm{s}}m}} + e{A_{{\rm{s}}m}} + e{E_{{\rm{ps}}m}} + e{A_{{\rm{ps}}m}}, $ |
| $ {e_{{\rm{rp}}m}} = e{E_{{\rm{r}}m}} + e{A_{{\rm{r}}m}} + e{E_{{\rm{pr}}m}} + e{A_{{\rm{pr}}m}}. $ |
结合GTF星型轮系的齿轮参数,参考标准ISO 1328-1: 1995,得到精度等级为5级下齿轮的制造、安装误差如表 2所示.
| 表 2 齿轮制造和安装误差 Table 2 Manufacturing and assembling error ofthe Gears |
利用弹性力学的势能原理考虑轮齿弯曲变形、剪切变形、轴向压缩变形、赫兹接触变形及轮体变形,求解啮合线上等效刚度[18-19].内外啮合齿轮副单齿啮合刚度Ke可表示为
| $ {K_e} = 1/\left( {\frac{1}{{{K_{{\rm{b1}}}}}} + \frac{1}{{{K_{{\rm{s1}}}}}} + \frac{1}{{{K_{{\rm{a1}}}}}} + \frac{1}{{{K_{{\rm{f1}}}}}} + \frac{1}{{{K_{{\rm{b2}}}}}} + \frac{1}{{{K_{{\rm{s2}}}}}} + \frac{1}{{{K_{{\rm{a2}}}}}} + \frac{1}{{{K_{{\rm{f2}}}}}} + \frac{1}{{{K_{\rm{h}}}}}} \right). $ |
式中:Kb为弯曲刚度,Ks为剪切刚度,Ka轴向压缩刚度,Kf轮体变形等效刚度,Kh为赫兹接触刚度.对单齿啮合刚度进行叠加,可以得到星型轮系单边斜齿轮时变外内啮合刚kps和kpr随输入转角θ变化曲线如图 11所示,从图 11中可以得到齿轮系统时变外啮合刚度的均值为

|
图 11 星型轮系人字齿时变啮合刚度 Figure 11 Time-varying meshing stiffness of the herringbone gears |
传动系统中各个星轮沿中心轮周向均布,受齿数影响,不同啮合副在啮合相位上会有所不同,这种差异将会影响各轮齿啮合副的时变啮合刚度和当量啮合误差.本文在处理人字齿星型齿轮传动中的啮合相位时,基于人字齿轮的特点并结合Parker的研究成果[20],啮合相位差计算公式如下:
| $ {\gamma _{sm}} = {z_s}{\psi _m}/2{\rm{ \mathsf{ π} }}, $ |
| $ {\gamma _{rm}} = - {z_r}{\psi _m}/2{\rm{ \mathsf{ π} }}{\rm{.}} $ |
式中:γsm表示星型轮系的各外啮合副相位差,γrm表示各内啮合副的相位差,zs、zr分别为太阳轮和齿圈的齿数.
3.4 中心轮浮动传动系统中心齿轮的浮动会导致侧隙的变化,假定太阳轮和内齿圈在x和y方向上引起的浮动为xs、ys,xr、yr则浮动所引起的外内啮合线位移Δsm和Δrm为
| $ {\Delta _{sm}} = - {x_s}\sin {\psi _{sm}} + {y_s}\cos {\psi _{sm}}, $ |
| $ {\Delta _{rm}} = - {x_r}\sin {\psi _{rm}} + {y_r}\cos {\psi _{rm}}, $ |
| $ {x_s} = {y_s} = {E_s} + 4/3{E_p}\cos {\alpha _s}, $ |
| $ {x_r} = {y_r} = {E_r} + 4/3{E_p}\cos {\alpha _r}. $ |
轴承刚度的各自由度均存在着耦合关系,各方向刚度也是时变的,由于滚动轴承多数耦合项较小,为简化计算,在动力学分析时不考虑轴承刚度的时变性,仅保留径向和轴向的刚度值[18].滚动轴承的刚度矩阵Kb可以简化为
| $ {\mathit{\boldsymbol{K}}_{\rm{b}}} = {\rm{diag}}\left[ {{k_{xx}};{k_{yy}};{k_{zz}};0;0;0} \right]. $ |
Romax被认为是权威的载荷分布计算软件,可实现机械传动产品设计及系统仿真分析[21],利用Romax软件建立整个系统的模型,提取系统中轴承各自由度的刚度值如表 3所示.
| 表 3 轴承支撑刚度 Table 3 Stiffness of bearing support |
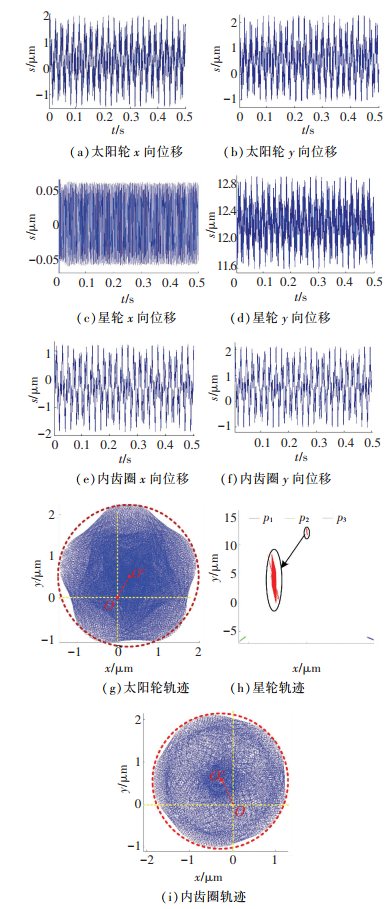
结合GTF人字齿星型轮系的动态激励以及额定工况(输入转速9 000 r/min,输入功率120 kW),求解系统动力学微分方程得到各齿轮节点的时域响应如图 12所示,由于人字齿两侧节点的振动规律相类似,因此以左侧为例进行分析.
|
图 12 齿轮节点时域响应 Figure 12 Time-domain response of the gear nodes |
由图 12(g)~(i)可知,各齿轮节点径向振动位移幅值在2 μm左右,中心齿轮构件由于偏心误差的存在使得其轨迹中心不再位于坐标原点O,这是造成系统内外啮合不均载的根本原因,与中心构件不同,星轮的受力状况较差,其振动轨迹为平面内的细长区域,与内外啮合力的合力方向一致.
由图 12(a)~(f)还可以看出,各齿轮节点x和y向振动位移也有一定差异,这是啮合误差和啮合相位差共同作用下使得系统并不完全对称的原因,这种现象也会引起系统的不均载.太阳轮和内齿圈作为中心轮,受力条件相似,其振动规律、幅值和轨迹都非常接近.但星轮的径向和切向振动规律(图 12(e)和12(f))差异较大,星轮y向(连心线方向)振动平衡位置不再是零点,而为一个正值,y向相比x向振动幅值大很多,这是因为星轮所受到的内外啮合力切向分力方向一致,而径向分力相反,叠加后相互抵消的结果.
4.2 星型轮系动态均载系数星型轮系的均载性能用动力学载荷分配不均匀系数来描述,简称动态均载系数.传动系统轮齿啮合力由弹性力和阻尼力组成,以Fsm与Frm分别表示GTF星型轮系内外啮合力:
| $ {F_{{\rm{s}}m}} = {k_{{\rm{s}}m}}\left( t \right){\delta _{{\rm{s}}m}} + {c_{{\rm{s}}m}}\left( t \right){{\dot \delta }_{{\rm{s}}m}}, $ |
| $ {F_{{\rm{r}}m}} = {k_{{\rm{r}}m}}\left( t \right){\delta _{{\rm{r}}m}} + {c_{{\rm{r}}m}}\left( t \right){{\dot \delta }_{{\rm{r}}m}}. $ |
虽然人字齿在结构上左右对称,不同于双悬臂支撑,单悬臂会导致系统的边界条件不再对称,使得人字齿两侧的均载性能不一致,将人字齿分为左右两侧分别计算:
| $ \delta _{{\rm{s}}m}^i = \mathit{\boldsymbol{V}}_{{\rm{s}}m}^i\mathit{\boldsymbol{q}}_{{\rm{s}}m}^i + {\Delta _{{\rm{s}}m}} + {e_{{\rm{s}}m}}\left( t \right),\left( {i = {\rm{L}},{\rm{R}}} \right) $ |
| $ \delta _{{\rm{r}}m}^i = \mathit{\boldsymbol{V}}_{{\rm{r}}m}^i\mathit{\boldsymbol{q}}_{{\rm{r}}m}^i + {\Delta _{{\rm{r}}m}} + {e_{{\rm{r}}m}}\left( t \right).\left( {i = {\rm{L}},{\rm{R}}} \right) $ |
定义某一时间节点上参与内外啮合人字齿左右两侧的均载系数为bsmL、bsmR和brmL、brmR:
| $ b_{{\rm{s}}m}^{\rm{L}} = 3F_{{\rm{s}}m}^{\rm{L}}/\sum\limits_{m = 1}^3 {F_{{\rm{s}}m}^{\rm{L}}} ,b_{{\rm{s}}m}^{\rm{R}} = 3F_{{\rm{s}}m}^{\rm{R}}/\sum\limits_{m = 1}^3 {F_{{\rm{s}}m}^{\rm{R}}} , $ |
| $ b_{{\rm{r}}m}^{\rm{L}} = 3F_{{\rm{r}}m}^{\rm{L}}/\sum\limits_{m = 1}^3 {F_{{\rm{r}}m}^{\rm{L}}} ,b_{{\rm{r}}m}^{\rm{R}} = 3F_{{\rm{r}}m}^{\rm{R}}/\sum\limits_{m = 1}^3 {F_{{\rm{r}}m}^{\rm{R}}} . $ |
把外内啮合人字齿各时间点星轮均载系数的最大值作为该时刻的均载系数,则人字齿内外啮合左右两侧的动态均载系数BsmL、BsmR和BrmL、BrmR为
| $ B_{{\rm{s}}m}^{\rm{L}} = \max \left( {b_{{\rm{s}}m}^{\rm{L}}} \right),B_{{\rm{s}}m}^{\rm{R}} = \max \left( {b_{{\rm{s}}m}^{\rm{R}}} \right), $ |
| $ B_{{\rm{r}}m}^{\rm{L}} = \max \left( {b_{{\rm{r}}m}^{\rm{L}}} \right),B_{{\rm{r}}m}^{\rm{R}} = \max \left( {b_{{\rm{r}}m}^{\rm{R}}} \right). $ |
取一段时间内外内啮合动态均载系数的最大值作为星型轮系的均载系数:
| $ B_{\rm{s}}^{\rm{L}} = \max \left( {B_{{\rm{s}}m}^{\rm{L}}} \right),B_{\rm{s}}^{\rm{R}} = \max \left( {B_{{\rm{s}}m}^{\rm{R}}} \right), $ |
| $ B_{\rm{r}}^L = \max \left( {B_{{\rm{r}}m}^{\rm{L}}} \right),B_{\rm{r}}^{\rm{R}} = \max \left( {B_{{\rm{r}}m}^{\rm{R}}} \right). $ |
在额定工况下,以5级精度为例,取安装、制造误差的极限值,通过求解在当量啮合误差下Hicks柔性销轴式人字齿星型轮系左右两侧的均载系数随时间的变化曲线如图 13所示.从图 13中可以看出, 3个星轮的均载系数变化规律相似,均呈现出周期性变化,但是由于啮合相位差和偏心误差的存在,使得星轮的均载系数呈现出均值和相位上的差异.从图 13中可以得到系统的外内啮合均载系数分别为:BsL=1.047、BsR=1.046、BrL=1.050、BrR=1.048,左侧的均载系数略大于右侧,内啮合系数略大于外啮合,这是由于人字齿右侧远离销轴支撑点,人字齿右侧的支撑刚度更小,均载性能更好,此外在相同的精度等级条件下,内齿圈的误差值略大,造成的不均载影响更大.

|
图 13 人字齿星型轮系均载系数 Figure 13 Load sharing coefficient of herringbone star gear transmission system |
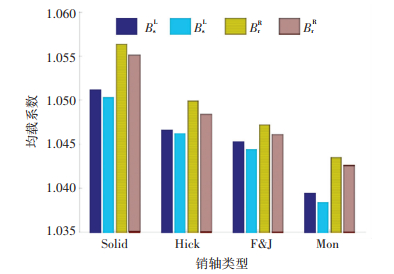
在其他条件相同的前提下,4种不同销轴支撑下人字齿星型轮系左右两侧内外啮合的均载系数如图 14所示.从图 14中可以看出, 其他3种销轴支撑下系统均载性能的规律同Hicks柔性销得到的结果类似,但相比于实心销轴,柔性销可以明显改善系统的均载性能,且Montestruc所改进的柔性销均载性能最佳,这与文献[6]的有限元仿真结果一致.
|
图 14 星型轮系均载系数 Figure 14 Load sharing coefficient of star gear trains |
为了单独分析齿轮的误差对系统均载性能的影响,以Hicks柔性销支撑的人字齿左侧内啮合为例,在制造误差、安装误差作用下得到系统的均载系数随误差变化曲线如图 15所示.从图 15可以看出:随着安装误差和制造误差的增大,系统的均载系数均逐渐增加,且基本上呈现出线性变化趋势,但比较制造误差和安装误差的单独影响发现,制造误差对均载系数的影响要明显大于安装误差.

|
图 15 误差对均载系数的影响 Figure 15 Influence of error on Load sharing coefficient |
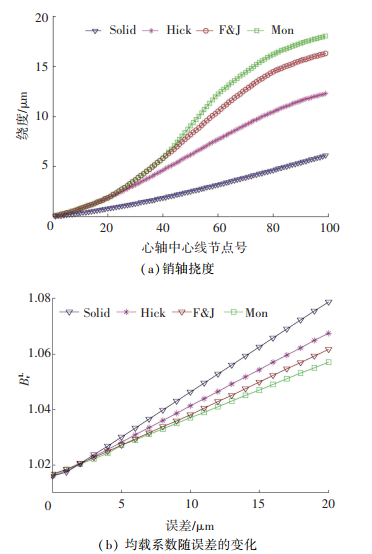
柔性销能够改善系统的均载性能,本质上为改变了齿轮的支撑刚度,理论和实践均表明:减小行星传动机构中各主要部件的支撑刚度能够有效改善系统均载性能,这主要是由于较低的支撑刚度能够有助于各部件自由浮动以补偿由于制造、安装和受载变形等因素造成的各类误差.在相同的载荷作用下得到4种销轴的变形如图 16(a)所示:相比于实心销轴,柔性销的刚度更小,且各种柔性销中Montestruc柔性销轴挠度最大、刚度最小;此外柔性销相比实心销轴会呈现“S”型变形,该性能可以保证齿轮轴线的平行,这对于改善人字齿两侧载荷的均匀性是很关键的. 4种不同结构的星轮销轴下的均载系数随误差变化如图 16(b)所示,从图 16(b)中可以看出相比于悬臂实心销轴,柔性销可以明显降低系统对误差的敏感性,改善系统均载性能,且随着销轴柔性的增加,系统均载性能逐渐提高.
|
图 16 不同柔性销结构对系统均载系数的影响 Figure 16 Influence of pin structure on load sharing coefficient |
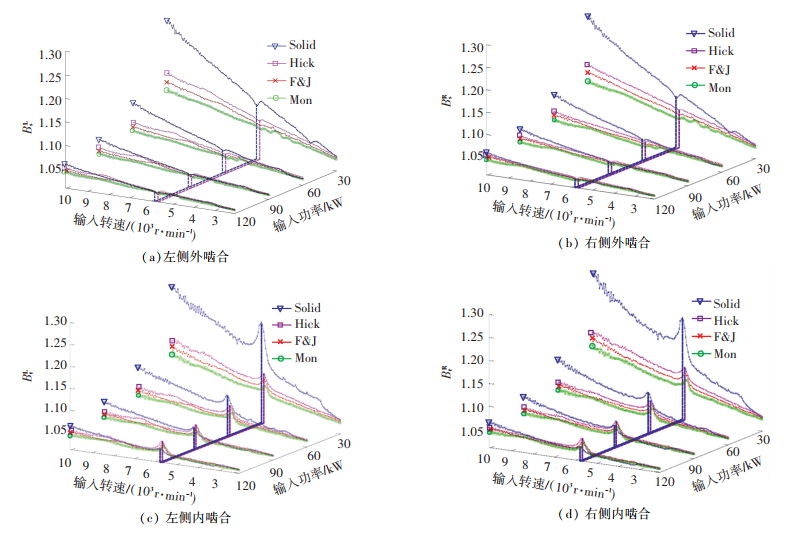
通过计算系统在不同功率下的均载系数随输入转速的变化如图 17所示,并结合系统的固有频率(表 4)分析均载系数变化,表 4中fi为系统第i阶固有频率,si为频率所对应的系统输入转速.受篇幅所限,本文仅列出了2种销轴的前12阶固有频率作为对比说明.
|
图 17 不同工况下的均载系数 Figure 17 Load sharing coefficient under different power |
| 表 4 系统固有频率 Table 4 Nature frequencyof system |
从图 17中可以看出,4种销轴支撑下系统的均载性能与转速和功率变化的趋势基本类似,无论内啮合还是外啮合,采用柔性销支撑的结构均载性能均要好过实心销轴,各功率下系统的均载系数随着输入转速的提高均呈增大趋势,但在共振点附近(图 17中实心销轴和Hick柔性销均载系数都在第10阶固有频率附近发生突变,4种销轴支撑下的系统的固有频率略有差异,但均对应表 4中的转速s10,另外两种销轴的规律也是类似)会出现均载系数突变的情况,且内外啮合的变化趋势相反,即内啮合的均载系数大幅增加,外啮合的则变小,但对整个系统而言,共振则大大降低了系统的均载性能.此外对比不同功率下的均载系数可以看出,随着功率增大,系统的均载性能变好,尤其是针对在功率较小的情况下,如P=30 kW时(该功率为风车状态下的功率,即发动机空中停车、燃烧室熄火或不工作时,气流通过未点燃的发动机并由于空气动力、转子惯性和阻力矩共同作用而带动发动机轴转动),柔性销改善系统均载性能的优势则更加突出,由此说明GTF发动机风扇驱动齿轮系统中采用柔性销的必要性.
5 结论1) 中心齿轮两个方向振动规律基本一致,而星轮径向和切向的振动规律差异较大,偏心误差的存在使中心轮振动的轨迹中心偏离理论位置,这是造成不均载的主要原因.
2) 当量啮合误差下系统内啮合的均载系数大于外啮合,且人字齿右侧的均载性能比左侧更好,随着误差的增大,系统的均载系数呈线性增加趋势,相比于安装误差,制造误差的对均载系数的影响要更大;与实心销轴相比,采用柔性销结构可以明显改善系统的均载性能,且随着销轴柔性增加,系统均载性能逐渐提高,对误差敏感性下降,柔性销结构中Montestruc所改进的柔性销刚度最小,均载性能最佳.
3) 系统的均载系数随着输入转速的增加呈增大趋势,系统的共振会导致系统的均载性能急剧下降,但对系统内外啮合的影响相反;随着系统承载功率的增大,系统均载性能变好,且功率越小,柔性销对改善系统的均载性能的优势越明显.
| [1] |
MA P, BOTMAN M. Load sharing in a planetary gear stage in the presence of gear errors and misalignment[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1985, 107(1): 4-10. DOI:10.1115/1.3258694 |
| [2] |
KAHRAMAN A. Load sharing characteristics of planetary transmissions[J]. Mechanism and Machine Theory, 1994, 29(8): 1151-1165. DOI:10.1016/0094-114x(94)90006-x |
| [3] |
BODAS A, KAHRAMAN A. Influence of carrier and gear manufacturing errors on the static load sharing behavior of planetary gear sets[J]. JSME International Journal Series C, Mechanical Systems, Machine Elements and Manufacturing, 2004, 47(3): 908-915. DOI:10.1299/jsmeimpt.ii.01.202.633 |
| [4] |
SINGH A. Application of a system level model to study the planetary load sharing behavior[J]. Journal of Mechanical Design, 2005, 127(3): 469-476. DOI:10.1115/1.1864115 |
| [5] |
袁擎宇, 朱如鹏, 朱自冰, 等. 两级星型齿轮传动静力学均载分析[J]. 机械科学与技术, 2004, 23(7): 789-792. YUAN Qingyu, ZHU Rupeng, ZHU Zibing, et al. Analysis of static load sharing in a 2-stage star gearing system[J]. Mechanical Science and Technology, 2004, 23(7): 789-792. DOI:10.3321/j.issn:1003-8728.2004.07.011 |
| [6] |
MONTESTRUC A N. Influence of planet pin stiffness on load sharing in planetary gear drives[J]. Journal of Mechanical Design, 2011, 133(1): 014501. DOI:10.1115/1.4002971 |
| [7] |
ZHU C C, XU X Y, LIU H J, et al. Research on dynamical characteristics of wind turbine gearboxes with flexible pins[J]. Renewable Energy, 2014, 68(7): 724-732. DOI:10.1016/j.renene.2014.02.047 |
| [8] |
谭援强, 胡聪芳, 张跃春, 等. 封闭差动行星齿轮箱动态均载性能试验研究[J]. 机械工程学报, 2016, 52(9): 28-35. TAN Yuanqiang, HU Congfang, ZHANG Yuechun, et al. Testing research on dynamic load sharing performance of encased differential planetary gearbox[J]. Journal of Mechanical Engineering, 2016, 52(9): 28-35. DOI:10.3901/JME.2016.09.028 |
| [9] |
杜进辅, 方宗德, 王宝宾, 等. 基于变形协调的行星轮系均载特性研究[J]. 航空动力学报, 2012, 27(5): 1166-1171. DU Jinfu, FANG Zongde, WNAG Baobin, et al. Study on load sharing behavior of planetary gear train based on deformation compatibility[J]. Journal of Aerospace Power, 2012, 27(5): 1166-1171. |
| [10] |
刘辉, 蔡仲昌, 项昌乐. 两级行星齿轮传动非线性啮合力频率耦合与动态特性研究[J]. 振动与冲击, 2015, 34(19): 13-23. LIU Hui, CAI Zhongchang, XIANG Changle. Frequency coupling and dynamic characteristics of nonlinear meshing force for two-stage planetary gears[J]. Journal of Vibration and Shock, 2015, 34(19): 13-23. DOI:10.13465/j.cnki.jvs.2015.19.003.ki.jvs.2015.19.003 |
| [11] |
朱伟林, 巫世晶, 王晓笋, 等. 安装误差对变刚度系数的复合行星轮系均载特性的影响分析[J]. 振动与冲击, 2016, 35(12): 77-85. ZHU Weilin, WU Shijing, WANG Xiaosun, et al. Influence of position errors on the load-sharing characteristics of compound planetary gear sets considering the variable stiffness coefficient[J]. Journal of Vibration and Shock, 2016, 35(12): 77-85. DOI:10.13465/j.cnki.jvs.2016.12.012.cnki.jvs.2016.12.012 |
| [12] |
REN F, QIN D T, LIM T C, et al. Study on dynamic characteristics and load sharing of a herringbone planetary gear with manufacturing errors[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(9): 1925-1934. DOI:10.1007/s12541-014-0547-y |
| [13] |
魏静, 张爱强, 秦大同, 等. 考虑结构柔性的行星轮系耦合振动特性研究[J]. 机械工程学报, 2017, 53(1): 1-12. WEI Jing, ZHANG Aiqiang, QIN Datong, et al. Coupling vibration analysis for planetary gear system considering flexible structure[J]. Journal of Mechanical Engineering, 2017, 53(1): 1-12. DOI:10.3901/JME.2017.01.001 |
| [14] |
HICKS R J. Load equalizing means for planetary pinions: U. S. Patent 3, 303, 713[P]. 1967-2-14.
|
| [15] |
FOX G P, JALLAT E. Epicyclic gear system: U. S. Patent 6, 994, 651[P]. 2006-2-7.
|
| [16] |
STRINGER D B. Geared rotor dynamic methodologies for advancing prognostic modeling capabilities in rotary-wing transmission systems[D]. Virginia: University of Virginia, 2008. http://adsabs.harvard.edu/abs/2008PhDT.......379S
|
| [17] |
HUEBNER K H, DEWHIRST D L, SMITH D E, et al. The finite element method for engineers[M]. New York: John Wiley & Sons, 2008.
|
| [18] |
常乐浩. 平行轴齿轮传动系统动力学通用建模方法与动态激励影响规律研究[D]. 西安: 西北工业大学, 2014. CHANG Lehao. A generalized dynamic model for parallel shaft gear transmissions and the influences of dynamic excitations[D]. Xi'an: Northwest Polytechnical University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10699-1015030990.htm |
| [19] |
CHEN Z G, SHAO Y M, LIM T C. Non-linear dynamic simulation of gear response under the idling condition[J]. International Journal of Automotive Technology, 2012, 13(4): 541-552. DOI:10.1007/s12239-012-0052-1 |
| [20] |
PARKER R G, LIN J. Mesh phasing relationships in planetary and epicyclic gears[J]. Journal of Mechanical Design, 2004, 126(2): 525-534. |
| [21] |
焦万铭, 杨珏, 马飞, 等. 变速器行星齿轮机构等强度优化设计[J]. 农业机械学报, 2015, 46(1): 359-364. JIAO Wanming, YANG Jue, MA Fei, et al. Equal strength optimal design of planetary gear transmission[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(1): 359-364. DOI:10.6041/j.issn.1000-1298.2015.01.050 |
 2018, Vol. 50
2018, Vol. 50



