装配序列在产品装配过程中扮演着极其重要的角色,不同的装配序列对产品成本、质量和可靠性等方面产生的影响是不同的.一个好的装配序列不仅应该满足产品所有的几何约束、精度要求,还应缩短装配过程的时间,减少成本[1].而且随着产品功能越来越丰富,质量要求越来越高,装配过程可靠性也将成为影响装配序列优选的重要因素.装配序列设计过程中一般存在多个可行的方案,优选出的装配序列方案应该有合理可行的装配路径、更可靠的装配过程、更少的夹紧件更换次数.因此,从若干可行装配序列方案中选择出最佳的装配序列,对产品生产很重要.
传统的装配序列决策过程一般是由工程师凭借其经验完成[2].但是对于复杂产品来说,不同装配序列意味着资源使用、效率、质量、可靠性的不同,即使经验丰富的工程师也难以在若干可行装配序列中优选出最好的装配方案.因此,建立健全装配序列评价指标体系和有效的决策方法就显得尤为必要.评价指标体系是进行装配序列优选的基础工作.目前,很多学者对装配序列的评价体系进行了研究:王孝义等[3]提出从零件级和序列级评价指标出发,采用基于有向图的序列比较法实现对装配序列的评价;袁宝勋等[4]提出从可行装配序列的零件级和系统级评价指标出发,采用基于区间逆序数和逼近理想解法对可行装配序列进行优选;Zhang等[5]从装配工艺的角度出发,提出整体级和单元级评价指标,并用最优解参考集法对可行装配序列进行评价;周开俊等[6]提出用熵权模糊综合评价法对装配资源、成本、时间、零件设计水平等指标进行评价,实现装配序列的优选.
目前,也有很多学者对装配序列决策方法进行了研究:Reddy B等[7]提出从可行装配序列花费成本角度出发,使用装配工具包设计软件对装配序列进行优选;LU.C等[8]提出从公差和装配间隙的角度出发,用转换矩阵计算可行装配序列的最终几何误差来实现装配序列的优选;Shiqi LI等[9]提出用共轴线约束和共平面约束等两种分层次法则将装配体分为两层,采用一种遍历迭代算法重组装配结构层次和更新装配姿势矩阵,实现对装配序列的优选.以上方法多是以获得最少的装配时间、最高的装配效率或最高装配精度为决策目标,考虑因素较单一且没有考虑装配可靠性因素.而由于制造业智能水平逐渐提高,设备可靠性越来越受重视,装配序列优选也会更加复杂,所以优选结果一般要求既能够满足精度、稳定性、可靠性等用户需求,又能满足工艺简单、成本低等生产企业要求.为了解决上述问题,本文提出一种基于多目标模糊综合评价的装配序列优选方法,从可靠性、精度、稳定性、工艺和成本等方面出发,将多属性决策方法应用到装配序列优选过程中.通过构建装配序列多目标综合评价指标体系,根据各评价指标的初始值和由FAHP确定的指标权重,使用消除和选择转换法对可行装配序列进行排序,并根据排序结果,从正、反面综合实现对可行装配序列优选.
1 装配序列评价指标体系建模装配序列评价指标体系对装配序列的评价结果以及产品生产都有较大影响,因此,要实现装配序列优选需建立科学合理的评价指标体系.评价指标体系的建立包括两个方面,一是确定所有评价指标及指标的层次关系;二是确定评价指标的算法.
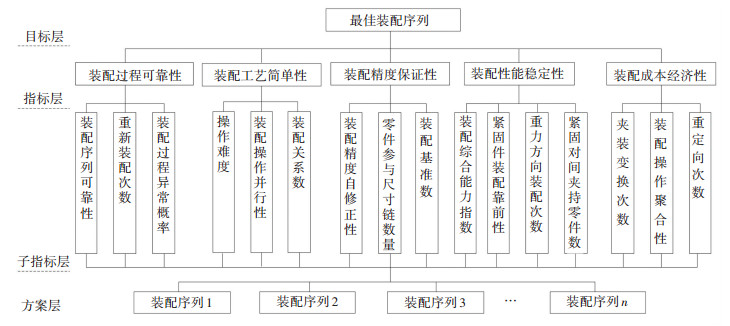
1.1 装配序列评价指标体系的建立要实现对装配序列评价,首先要确定相应评价指标.在企业调研基础上结合工程实际,根据专家意见提出16个对产品装配序列确定有影响的评价指标, 并根据指标属性以及对装配资源使用情况的影响将评价指标分为5类,评价指标层次结构模型如图 1所示.
|
图 1 装配序列评价指标层次模型 Figure 1 The hierarchy model of evaluation index for assembly sequence |
文献[3, 6, 10]中提出了零件级评价指标,然而由于装配时所需装配零件均已确定,各零件的属性值(质量、精度、对称性等)也是固定不变的,所以装配过程中已确定不变的零件属性值对装配序列的质量影响并不显著.如果从零件先后安装顺序不同引起装配质量不同的角度出发,面对多零件装配体时,评价其装配序列需按照不同零件属性值定义所有零件排序的最优参考序列(或标准序列).若有n个评价指标,m个装配序列,则需定义最优参考序列n×m次,这样计算过程相当繁杂,且工作量太大.所以本文提出从装配序列整体出发,从多目标角度研究不同装配序列对装配资源使用情况的影响,以致能够快速、准确地优选出最佳装配方案.
1.2 评价指标含义及计算方法装配过程可靠性是指按照给定的装配序列在规定条件下和规定的时间内,保证装配出来的产品具有规定可靠性水平的能力[11];装配工艺简单性是指在连续装配过程中,装配序列的工艺复杂程度;装配精度保证性是指可行装配序列精度指标在装配过程中保持正常的程度;装配性能稳定性是指在装配过程中装配零件在装配力和自身重力作用下的稳定程度;装配成本经济性是指实现装配序列所需要花费成本的经济程度.
在此,定义5个评价指标为U1~U5,子评价指标为Kj,评价指标下的属性值为kmj,j(1~16)为子评价指标序号,m为可行装配序列编号.
1) 装配序列可靠度K1.指装配体最后形成的装配正常概率.借鉴文献[12]的方法,在分析装配序列各工步装配异常概率的基础上,求得不同装配序列的装配过程可靠度.装配过程中,有一道工步装配异常,整个装配质量就会产生异常,又因为装配质量正常概率和异常概率之和为1,所以,装配序列的异常概率可根据各个工步故障率求得.设有n道装配工步,Pci表示第i道工步的正常概率,则装配序列的可靠度的属性值km1为
| $ k_m^1 = \prod\limits_{j = 1}^m {{P_{Rj}}\prod\limits_{i = m + 1}^n {{P_{ci}}} } . $ | (1) |
式中:j=1, 2, …, m;i=m+1, m+2, …, n;
2) 重新装配次数K2.指装配过程出现装配失效后,需要对装配体重新进行装配的次数,其主要反映了装配序列失效后的修正能力,其属性值越大对装配体进行重装的次数越多,表明失效序列的修正性越差,这与可靠性中的维修性相契合.在此,定义其属性值km2为装配序列的平均重新装配次数,即
3) 装配过程异常概率K3.指装配过程中产生装配异常的概率,其反映装配序列出现故障工步的数量在总工步中的占比,占比越大体现了装配序列的合理性越差.装配过程异常概率越大,装配序列出现故障的次数越多,则装配序可靠性越差.在此,定义其属性值
4) 操作难度K4.指工人实施装配序列的可操作性.操作难度通常从操作过程的可视性、可达性、操作风险以及操作条件等方面进行评价.在对其属性值量化过程中,若全部考虑这些因素,则计算比较繁杂.为简化计算过程,在此,借鉴模糊理论定义操作难度分为:相当难、较难、一般、稍简单、简单等5个等级,每个等级对应难度值分别为:1、0.8、0.6、0.4、0.2.计算时,根据实施可行装配序列的难度等级,选取相应难度值进行量化.
5) 操作并行性K5.指装配过程中存在若干子装配体可以同时进行装配的程度,其属性值km5越大,序列的邻界装配路径越短,装配时可以分开装配的子装配体就越多,相应的实施装配序列所花费的时间也就越少.将装配顺序表示为树形结构时,树的深度越小,则该装配过程并行性越好.采用装配树深度值差值法,其属性值km5可以表示为:km5=(tmax-ti)/(tmax-tmin).其中,tmax为可行装配序列装配树的最大深度值,tmin为最小深度值,ti为当前装配顺序深度值.
6) 装配关系数K6.指与装配零件有联接关系、装配关系的其他装配零件的数量,反映了零部件之间的约束关系,其值越大,子装配体间的装配关系数越多,会使产品装配工艺复杂,提高装配的操作要求.在此定义,其属性值km6等于装配体装配关系系数,即
7) 装配精度自修正性K7.在装配过程中,由于后道工序可以修正前道工序产生的误差,所以定义装配过程误差修正系数表示装配精度保证性.设装配过程中s个关键精度样本,定义装配过程的误差修正系数为
| $ k_m^7 = \left( {\sum\limits_{i = 1}^s {\frac{{i \times \left( {\left| {{d_{i1}}} \right| - \left| {{d_{in}}} \right|} \right)}}{{{\rm{sig}}\left( {\mathop {\max }\limits_j {D_i}\left( j \right)} \right)\mathop {\max }\limits_j {D_i}\left( j \right)}}} } \right)/\sum\limits_{i = 1}^s i . $ | (2) |
式中i=1, 2, …, s; j=1, 2, …, n;sig(x)是变量x的符号函数;di1, din分别表示装配过程中首尾工序的装配误差,Di(j)=|di(j)-di(j-1)|表示第i个关键精度样本的第j道装配工序对前道工序的装配误差修正量.
8) 参与尺寸链数量K8.指装配零件参与尺寸链的次数,其属性值km8为零件参与尺寸链的数量.装配零件参与尺寸链次数越多,则影响整体装配精度的可能性越大,越应提前装配.
9) 装配基准数K9.指装配时装配体作为其他装配体基准的次数,其属性值km9越大的装配体,应优先装配.
10)装配综合能力指数K10.综合工序能力指数Cpk常被用来衡量装配性能的稳定性.单个工序能力指数Cpki的大小用装配体轴孔特征的波动及异常来表示:
由于不同工序对装配体最终装配质量影响程度不同,设装配序列有n个工序,第i个工序的工序能力指数为Cpki,利用专家打分法确定不同工序的权重值w,则定义装配过程的综合能力指数为
| $ k_m^{10} = \sum\limits_{i = 1}^n {{C_{pki}}{w_i}} . $ | (3) |
11)紧固件装配靠前性K11.指装配时紧固件靠前装配的程度.可行装配序列中紧固件越靠前装配,装配其他组件时对已紧固的装配体影响越小,装配时装配序列的稳定性越好.在此,定义紧固件装配顺序平均值作为衡量紧固件装配靠前性指标,即
12)重力方向装配次数K12.指装配体在重力方向上的装配数量.装配时,重力方向被认为是最优的装配方向,该方向装配次数越多,则装配序列越好.其属性值km12等于装配过程中重力方向装配的总次数.
13)紧固对间夹持零件数K13.具有紧固关系的一对零件称为紧固对,紧固对之间所夹持的零件数量越少,装配体稳定性越好.在此,定义其属性值km13为紧固对间的平均零件数作,即
14)夹装变换次数K14.装配序列的夹装变换次数越少,则装配效率越高,经济性就越好.其属性值为
| $ k_m^{14} = \sum\limits_{i = 1}^Z {{T_{cn}}\left( {{T_{i - 1}},{T_n}} \right)} . $ | (4) |
其中
15)操作聚合性K15.指装配时零件集中完成装配的程度,其值越大,经济性越好.设装配过程的总装配操作次数为dmax,装配操作种类为dmin,所以操作种类变换的最少数目为dmin-1,最多为dmax-1,则其属性值为
| $ k_m^{15} = \left( {{d_{\max }} - 1 - {d_{\min }}} \right)/\left( {{d_{\max }} - {d_{\min }}} \right). $ | (5) |
16)重定向次数K16.指装配体在装配过程中装配方向改变的次数.其值越大,装配时操作数越多,需花费的装配成本越高.因此装配时其值越小越好.其属性值km16等于装配过程中装配体装配方向改变的次数.
2 基于FAHP的装配序列评价指标重要性确定层次分析法(Analytic Hierarchy Process,AHP)是美国运筹学家Saaty于20世纪70年代中期提出的一种实用层次权重分析方法[13]. AHP基本思想是将任意指标进行两两比较,并对结果主观给出精确比较值,然后将比较结果组成判断矩阵,通过判断矩阵求解所有指标的权重.
对于装配序列整体来说,各指标之间的比重关系具有一定的模糊性和不确定性,因此,在确定各指标相对于装配序列的权重过程中,需要考虑指标之间关系的模糊性或不明确性.在各指标关系确定过程中,相对于精确的数值,专家往往也会给出一些不明确的关系比例,例如专家一般会给出A比B稍微重要,而不是A是B的1.2倍关系.因此,用任意指标进行两两比较,并主观赋值的传统AHP法确定指标间各自的权重是不合适的,进行两两比较时指标间关系的不确定性应该被考虑[14].
评价指标两两比较过程中,用一个区间值去表示两指标间的关系比用一个固定数值表示更合理.这是因为在比较过程中指标间关系存在的模糊性使决策者往往无法用准确数字去表达他们对某指标的偏爱程度[15].由于模糊语言法可以合适地表达决策者对于某事物的的喜欢或厌恶程度,因此,由三角模糊数或梯形模糊数表示隶属度的语言值很适合表达人们对于某指标的偏爱程度.综上所述,在一些没有明确关系的指标比较中,使用FAHP法确定各指标权重比传统的AHP法更适合、有效.
为了更好地利用FAHP,一些学者提出了相应的方法,例如:模糊最小二乘法、综合程度分析法、直接模糊法和模糊偏爱法. CHANG[16]提出了一种新方法:用三角模糊数表示FAHP的指标两两比较范围,并用程度分析法处理指标两两比较后的综合程度值.本文应用他提出的程度分析法确定可行装配序列评价指标各自的权重.一个三角模糊数被定义为
| 表 1 模糊判断矩阵元素标度 Table 1 Value of fuzzy elements in pairwise comparison matrix |
计算过程基本思路为:首先,将同层次指标进行相对重要性评价,并用三角模糊标度表示指标两两比较的结果,然后把所有比较结果组成模糊判断矩阵;根据模糊判断矩阵,计算每个指标的初始权重;然后将各指标的初始权重两两比较,并取指标Kj(j=1, 2, …, n)的最终权重为其初始权重D(Kj)与其他元素的初始权重两两比较后结果的最小值;最后将各指标的权重标准化即可得到各指标的权重值.
基于FAHP的装配序列评价指标重要性计算过程包括以下步骤:
1) 构造三角模糊判断矩阵.设评价指标K1, K2, …, Kn进行两两重要性比较得到的模糊判断矩阵为A=(kij)n×n.模糊判断矩阵为互反矩阵,其计算公式如下:
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\left( {1,1,1} \right)}&{\left( {{l_{12}},{m_{12}},{r_{12}}} \right)}& \cdots &{\left( {{l_{1n}},{m_{1n}},{r_{1n}}} \right)}\\ {\left( {\frac{1}{{{r_{12}}}},\frac{1}{{{m_{12}}}},\frac{1}{{{l_{12}}}}} \right)}&{\left( {1,1,1} \right)}& \cdots &{\left( {{l_{2n}},{m_{2n}},{r_{2n}}} \right)}\\ \vdots&\vdots&\ddots&\vdots \\ {\left( {\frac{1}{{{r_{1n}}}},\frac{1}{{{m_{1n}}}},\frac{1}{{{l_{1n}}}}} \right)}&{\left( {\frac{1}{{{r_{2n}}}},\frac{1}{{{m_{2n}}}},\frac{1}{{{l_{2n}}}}} \right)}& \cdots &{\left( {1,1,1} \right)} \end{array}} \right]. $ | (6) |
式中i, j=1, 2, …, n.
2) 确定初始权重.定义指标Kj初始权重D(Kj)计算公式为
| $ D\left( {{K^j}} \right) = \sum\limits_{j = 1}^n {{k_{ij}}} \div \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{k_{ij}}} } = \frac{{\left( {\sum\limits_{j = 1}^n {{l_{ij}}} ,\sum\limits_{j = 1}^n {{m_{ij}}} ,\sum\limits_{j = 1}^n {{r_{ij}}} ,} \right)}}{{\left( {\sum\limits_{i,j = 1}^n {{l_{ij}}} ,\sum\limits_{i,j = 1}^n {{m_{ij}}} ,\sum\limits_{i,j = 1}^n {{r_{ij}}} ,} \right)}}. $ | (7) |
式中i、j=1, 2, …, nk.
3) 求各指标最终权重.指标Kj的最终权重d(Kj)为其初始权重D(Kj)与其他元素的初始权重两两比较后结果的最小值,因此要确定指标Kj的最终权重d(Kj),需将指标Kj的初始权重D(Kj)与其他指标初始权重进行两两比较.
设指标Ki和指标Kj的初始权重分别为D(Ki)=(li, mi, ui)、D(Kj)=(lj, mj, uj),则D(Ki)>D(Kj)的可能度用三角模糊函数V(D(Ki)>D(Kj))定义为
| $ V = \left\{ \begin{array}{l} 1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{m_i} > {m_j};\\ \frac{{{l_j} - {u_j}}}{{\left( {{m_i} - {u_i}} \right) - \left( {{m_j} - {l_j}} \right)}},\;\;\;\;\;{m_i} \le {m_j},{u_i}{ \ge _j};\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}}{\rm{.}} \end{array} \right. $ | (8) |
取指标Kj的最终权重d(Kj)为其初始权重D(Kj)与其他元素的初始权重两两比较后结果的最小值,即
| $ d\left( {{K^j}} \right) = \min \left\{ {V\left( {{D_j} > {D_1}} \right), \cdots ,V\left( {{D_j} > {D_n}} \right)} \right\}. $ | (9) |
同理,可计算出其他评价指标权重,然后可得各指标的最终权重集W′:
| $ W' = \left( {d\left( {{K^1}} \right),d\left( {{K^2}} \right), \cdots ,d\left( {{K^n}} \right)} \right). $ |
4) 归一化权重.将指标K1的最终权重值归一化,得到其归一化权重为
| $ {w_{{K^1}}} = \frac{{d\left( {{K^1}} \right)}}{{d\left( {{K^1}} \right) + d\left( {{K^2}} \right) + \cdots + d\left( {{K^n}} \right)}}. $ | (10) |
同理,可得其他指标的归一化权重.所以各指标的归一化权重集为
| $ W = \left( {{w_{{K^1}}},{w_{{K^2}}}, \cdots ,{w_{{K^n}}}} \right). $ |
消除和选择转换法(Elimination and Choice Translating Reality, ELECTRE)是由B.Roy提出的决策方法,该方法通过评估多指标方案的最大优势和最小劣势来确定最优方案[17],目前已广泛应用于各种方案的决策. ELECTRE可以分为5种类型,分别为ELECTREⅠ、Ⅱ、Ⅲ、Ⅳ和TRI. 5种方法的基础思想是一样的,但要根据决策问题的类型来选择应用哪种方法. ELECTREⅠ适用于选择类问题,ELECTREⅡ、Ⅲ、Ⅳ适用于排列问题,ELECTRE TRI使用于分配问题[18].本文中所要解决的问题是在众多可行装配序列中优选出最佳装配序列,因此选择使用ELECTREⅠ法.该方法将不同方案之间的优劣对比程度用目标一致性和不一致性两种类型表示,通过分析一致性评价指标和不一致性评价指标的值得到不同方案的优势值和劣势值,再根据目标值的最大值选择最优装配方案.
传统的ELECTRE法在计算过程中,各指标权重是专家主观给出的精确值,可能存在表达不准确的情况,为了更合理地表达各指标的权重,在此,将应用FAHP求出的各指标权重作为ELECTRE法中加权矩阵的权重.
假定A1, A2, …, Am为m个可能的装配序列实施方案,K1, K2, …, Kn为n个装配方案的评价指标,定义kij为方案Ai中Kj指标的值,矩阵[kij]n×m为决策矩阵,wn为评价指标, Cn由FAHP计算得到的权重.
ELECTRE Ⅰ法的计算流程如下:
1) 决策矩阵加权计算.考虑决策矩阵不同指标量纲间的差异,首先标准化决策矩阵[kij]n×m,得到标准化矩阵R=[rij]m×n,其中
| $ {r_{ij}} = \frac{{k_i^j}}{{\sqrt {\sum\limits_{i = 1}^m {x_{ij}^2} } }}, $ | (11) |
式中i=1, 2, …, m;j=1, 2, …, n.
定义标准化矩阵的加权矩阵如下:
| $ \mathit{\boldsymbol{V}} = \mathit{\boldsymbol{R}} \times \mathit{\boldsymbol{W = }}\left[ {\begin{array}{*{20}{c}} {{r_{11}} \cdot {w_1}}&{{r_{12}} \cdot {w_2}}& \cdots &{{r_{1n}} \cdot {w_n}}\\ {{r_{21}} \cdot {w_1}}&{{r_{22}} \cdot {w_2}}& \cdots &{{r_{2n}} \cdot {w_n}}\\ \vdots&\vdots&\ddots&\vdots \\ {{r_{m1}} \cdot {w_1}}&{{r_{m2}} \cdot {w_2}}& \cdots &{{r_{mn}} \cdot {w_n}} \end{array}} \right], $ | (12) |
式中0≤w1, w2, …, wn≤1.
2) 确定一致和不一致区间集合.假设A={A1, A2, …, Am}表示可行装配序列方案的集合,分别划分装配序列评价指标为一致性区间集合(C(a, b))和不一致区间集合(D(a, b)). C(a, b)表示一致性区间集合为
| $ {C_{\left( {a,b} \right)}} = \left\{ {j\left| {{x_{aj}} \ge {x_{bj}}} \right.} \right\}. $ | (13) |
作为C(a, b)的补偿,不一致区间集合D(a, b)的计算公式为
| $ {D_{\left( {a,b} \right)}} = \left\{ {j\left| {{x_{aj}} < {x_{bj}}} \right.} \right\} = J - {C_{\left( {a,b} \right)}} = {J_0}. $ | (14) |
3) 计算一致性区间指数矩阵.为准确反映决策者对方案的偏好程度,定义方案Aa和Ab之间的一致性区间指数集合Cab为
| $ {C_{ab}} = \sum\limits_{j \in {C_{ab}}} {{w_j}} . $ | (15) |
一致性指数表示方案Aa优于Ab的程度.一致性区间指数矩阵如下:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} - &{{C_{12}}}& \cdots &{{C_{1n}}}\\ {{C_{21}}}& -&\cdots &{{C_{2n}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{C_{m1}}}&{{C_{m2}}}& \cdots&- \end{array}} \right] $ | (16) |
4) 计算不一致性区间指数矩阵.首先应用不一致性指数Dab代表方案Aa和Ab之间的不满程度,其定义为
| $ {D_{ab}} = \frac{{\mathop {\max }\limits_{j \in {J_0}} \left| {{v_{aj}} - {v_{bj}}} \right|}}{{\mathop {\max }\limits_j \left| {{v_{aj}} - {v_{bj}}} \right|}}. $ | (17) |
不一致区间指数矩阵可定义为
| $ D = \left[ {\begin{array}{*{20}{c}} - &{{D_{12}}}& \cdots &{{D_{1n}}}\\ {{D_{21}}}& -&\cdots &{{D_{2n}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{D_{m1}}}&{{D_{m2}}}& \cdots&- \end{array}} \right]. $ | (18) |
5) 计算净优势值和劣势值.以ca和da分别表示装配序列的优势值和劣势值. ca.为方案a相对其他方案的优势指标加权之和减去其方案相对a的优势指标加权之和,反映了方案a优势指标在方案集中的综合优势程度.优势值越大,说明装配方案的综合优势程度越高,则装配方案越好
| $ {c_a} = \sum\limits_{\begin{array}{*{20}{c}} {b = 1}\\ {b \ne a} \end{array}}^n {{C_{ab}}} - \sum {\sum\limits_{\begin{array}{*{20}{c}} {b = 1}\\ {b \ne a} \end{array}}^n {{C_{ba}}} } . $ | (19) |
同理,da为方案a相对其他方案的劣势指标加权之和减去其方案相对a的劣势指标加权之和,反映了方案a劣势指标在方案集中的综合劣势程度.劣势值越小,说明装配方案的综合劣势程度越小,则装配方案越好.
| $ {d_a} = \sum {\sum\limits_{\begin{array}{*{20}{c}} {b = 1}\\ {b \ne a} \end{array}}^n {{D_{ab}}} } - \sum {\sum\limits_{\begin{array}{*{20}{c}} {b = 1}\\ {b \ne a} \end{array}}^n {{D_{ba}}} } . $ | (20) |
6) 计算净优势度.净优势值ca和净劣势值da的大小反映了装配序列的优良性.当各方案依据ca和da的排序结果不一致时,可借鉴文献[19]的方法,利用方案净优势值和净劣势值之间的距离来表示方案的优良性.若ca越大且da越小,则方案a在方案集中越好.装配序列的净优势度为
| $ {r_a} = {c_a} - {d_a}. $ | (21) |
ra反映了装配序列净优势值和净劣势值之间的距离,其值越大,装配序列也就越好.评价过程中若出现不同方案净优势度一样的情况,则说明两种方案具有等同的优良性,在进行装配序列优选时,可根据决策者对不同方案间优势指标和劣势指标的偏向程度对方案进行选择.
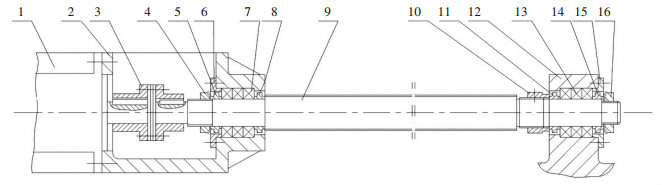
4 实例分析下面对某企业机床的传动系统装配序列进行实例分析.该企业的车削中心和加工中心所采用的传动系统基本一致,结构图如图 2所示. 2种机床分属于2个不同的装配车间,传动系统装配过程由各自车间的工艺员制定,由于不同的工艺员操作习惯和装配理念不同,所以目前传统系统共有4种不同的装配顺序,如图 3所示.现对4种装配序列进行综合评价,从中优选出最佳的装配方案.
|
1.电机; 2.电机座; 3.联轴器; 4.锁紧螺母; 5.隔套; 6.端压盖; 7.左轴承; 8.隔套; 9.滚珠丝杆; 10.锁紧螺母; 11.隔套; 12.丝杆座; 13.右轴承; 14.隔套; 15.端压盖; 16.锁紧螺母 图 2 传动系统装配图 Figure 2 The assembly drawing of drive system |
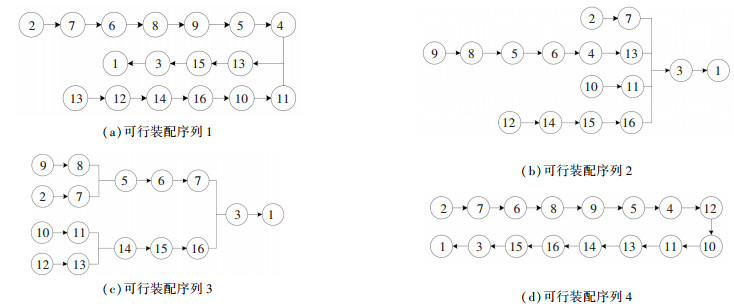
|
图 3 可行装配序列 Figure 3 The diagram of feasible assembly sequence |
步骤1:因为有4个可行装配序列,所以建立可行装配序列方案集A={A1, A2, A3, A4}.根据第2节确定的评价指标和指标的计算方法,求得各可行装配序列的评价指标属性值,各指标的基本属性值如表 2所示.
| 表 2 可行装配序列评价指标的值 Table 2 The value of feasible assembly sequence evaluation index |
步骤2:确定各评价指标的权重.一般情况下,不同的企业对于装配序列评价点的侧重有所不同,例如:航天设备对精度、可靠性等要求比较高,电柜门等产品则注重产品的经济性.因此,在确定装配序列各评价指标权重的过程中,要结合产品的实际需求,确定出合理的指标权重值.本例中所举的机床传动系统在实际使用过程中,对于装配精度和可靠性的指标要求比较高,因此在评价时对这两个指标有所偏重.
1) 模糊判断矩阵.由5位专家分别对5个评价指标进行模糊评价.根据式(6)将模糊数整合后可得模糊判断矩阵为
| $ \mathit{\boldsymbol{A = }}\\\begin{array}{*{20}{c}} {{U^1}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{U^2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{U^3}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{U^4}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{U^5}}&{}\\ {\left[ {\begin{array}{*{20}{c}} {\left( {1,1,1} \right)}&{\left( {0.83,1.33,1.83} \right)}&{\left( {0.83,1.33,1.83} \right)}&{\left( {0.46,0.60,0.85} \right)}&{\left( {1.17,1.67,2.17} \right)}\\ {\left( {0.55,0.75,1.20} \right)}&{\left( {1,1,1} \right)}&{\left( {0.67,1,2} \right)}&{\left( {0.55,0.75,1.20} \right)}&{\left( {0.55,0.75,1.20} \right)}\\ {\left( {0.55,0.75,1.20} \right)}&{\left( {0.5,1,1.5} \right)}&{\left( {1,1,1} \right)}&{\left( {0.46,0.60,0.85} \right)}&{\left( {0.83,1.33,1.83} \right)}\\ {\left( {1.17,1.67,2.17} \right)}&{\left( {0.83,1.33,1.83} \right)}&{\left( {1.17,1.67,2.17} \right)}&{\left( {1,1,1} \right)}&{\left( {1.5,2,2.5} \right)}\\ {\left( {0.46,0.60,0.85} \right)}&{\left( {0.83,1.33,1.83} \right)}&{\left( {0.55,0.75,1.20} \right)}&{\left( {0.40,0.50,0.67} \right)}&{\left( {1,1,1} \right)} \end{array}} \right]}&{\begin{array}{*{20}{c}} {{U^1}}\\ {{U^2}}\\ {{U^3}}\\ {{U^4}}\\ {{U^5}} \end{array}} \end{array} $ |
2) 确定指标初始权重.设各评价指标初始权重集为:U={D(U1), D(U2), D(U3), D(U4), D(U5)}= {装配过程可靠性,装配工艺简单性,装配精度保持性,装配性能稳定性,装配成本经济性}.将模糊判断矩阵值代入式(7),得各指标的初始权重分别为
| $ D\left( {{U^1}} \right) = \left( {0.119,0.222,0.387} \right), $ |
| $ D\left( {{U^2}} \right) = \left( {0.092,0.159,0.333} \right), $ |
| $ D\left( {{U^3}} \right) = \left( {0.093,0.175,0.322} \right), $ |
| $ D\left( {{U^4}} \right) = \left( {0.158,0.287,0.487} \right), $ |
| $ D\left( {{U^5}} \right) = \left( {0.090,0.156,0.280} \right). $ |
3) 确定指标最终权重.将指标U1和其他指标的初始权重带入式(8),则指标Kj的初始权重D(Kj)与其他指标初始权重进行两两比较的结果为
| $ V\left( {{U^1} > {U^2}} \right) = 1,V\left( {{U^1} > {U^3}} \right) = 1, $ |
| $ \begin{array}{l} V\left( {{U^1} > {U^4}} \right) = \frac{{0.158 - 0.387}}{{\left( {0.222 - 0.387} \right) - \left( {0.287 - 0.158} \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0.779,\\ V\left( {{U^1} > {U^5}} \right) = 1. \end{array} $ |
根据式(9)可得指标U1的最终权重d(U1):
| $ d\left( {{U^1}} \right) = \min \left( {1,1,0.779,1} \right) = 0.779. $ |
同理,可得其他指标的最终权重:
| $ d\left( {{U^2}} \right) = 0.579,d\left( {{U^3}} \right) = 0.595, $ |
| $ d\left( {{U^4}} \right) = 1,d\left( {{U^5}} \right) = 0.483. $ |
所以评价指标最终权重集为
| $ W' = \left( {0.779,0.579,0.595,1,0.483} \right). $ |
4) 归一化权重向量
根据式(10)将各指标最终权重标准化,得各指标的标准化权重集
| $ W = \left( {0.227,0.168,0.173,0.291,0.141} \right). $ |
同理,可得子评价指标层各评价指标的权重,如表 3所示(括号内数值为一级指标与二级指标权之积,含义为子指标相对于总目标权重).
| 表 3 各评价指标的权重 Table 3 The weights of each evaluation index |
步骤3:对可行装配序列进行决策.评价指标中,K1, K5, K6, K7, K8, K9, K10, K11, K12, K13, K15属于越大越优型指标,K2, K3, K4, K5, K14, K16属于越小越优型指标.在对可行装配序列进行评价时,为了消除数据间的差异性,利用式(11)对数据进行量纲归一化处理,处理后的数据如表 4所示.
| 表 4 评价指标属性值归一化处理后数据 Table 4 The attribute value of normalized data for evaluation index |
将量纲标准化处理后的各指标值及根据FAHP确定的各指标相应权重代入式(12),可得标准化矩阵的加权矩阵:
| $ \mathit{\boldsymbol{V}} =\\ \left[ {\begin{array}{*{20}{c}} {0.047}&{0.023}&{0.043}&{0.035}&{0.027}&{0.024}&{0.030}&{0.023}&{0.024}&{0.044}&{0.038}&{0.047}&{0.030}&{0.020}&{0.023}&{0.021}\\ {0.048}&{0.015}&{0.044}&{0.023}&{0.045}&{0.015}&{0.032}&{0.026}&{0.022}&{0.043}&{0.035}&{0.037}&{0.035}&{0.024}&{0.022}&{0.025}\\ {0.048}&{0.030}&{0.043}&{0.023}&{0.029}&{0.021}&{0.033}&{0.032}&{0.027}&{0.040}&{0.024}&{0.037}&{0.046}&{0.028}&{0.019}&{0.030}\\ {0.047}&{0.023}&{0.042}&{0.035}&{0.022}&{0.028}&{0.035}&{0.032}&{0.029}&{0.038}&{0.014}&{0.028}&{0.035}&{0.024}&{0.020}&{0.025} \end{array}} \right]. $ |
根据式(13)可得,评价指标的一致性指标集合为
| $ {C_{\left( {1,2} \right)}} = \left\{ {3,9,10,11,12,14,15,16} \right\} $ |
| $ {C_{\left( {1,3} \right)}} = \left\{ {2,3,10,11,12,14,15,16} \right\}, $ |
| $ {C_{\left( {1,4} \right)}} = \left\{ {1,5,6,10,11,12,14,15,16} \right\}, $ |
| $ {C_{\left( {2,1} \right)}} = \left\{ {1,2,4,5,6,7,8,13} \right\}, $ |
| $ {C_{\left( {2,3} \right)}} = \left\{ {2,5,6,10,11,12,15} \right\}, $ |
| $ {C_{\left( {2,4} \right)}} = \left\{ {1,2,4,5,6,10,11,12,15} \right\}, $ |
| $ {C_{\left( {3,1} \right)}} = \left\{ {1,4,5,6,7,8,9,13} \right\}, $ |
| $ {C_{\left( {3,2} \right)}} = \left\{ {1,3,4,7,8,9,13} \right\}, $ |
| $ {C_{\left( {3,4} \right)}} = \left\{ {1,4,5,6,10,11,12,13} \right\}, $ |
| $ {C_{\left( {4,1} \right)}} = \left\{ {2,3,4,7,8,9,13} \right\}, $ |
| $ {C_{\left( {4,2} \right)}} = \left\{ {3,7,8,9,13,14,16} \right\}, $ |
| $ {C_{\left( {4,3} \right)}} = \left\{ {2,3,7,8,9,14,15,16} \right\}. $ |
将各评价指标的一致性集合和不一致性集合代入式(15)、(16),得一致性区间指数矩阵为
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} - &{0.495}&{0.490}&{0.561}\\ {0.505}& - &{0.513}&{0.568}\\ {0.510}&{0.487}& - &{0.553}\\ {0.439}&{0.432}&{0.447}& - \end{array}} \right]. $ |
根据式(19),4个可行装配方案的净优势值分别为
| $ \begin{array}{l} {c_1} = \sum\limits_{b = 1}^4 {{C_{1b}}} - \sum\limits_{b = 1}^4 {{C_{b1}}} = \left( {0.495 + 0.490 + 0.561} \right) - \\ \;\;\;\;\;\;\left( {0.505 + 0.510 + 0.439} \right) = 0.093, \end{array} $ |
| $ \begin{array}{l} {c_2} = \sum\limits_{b = 1}^4 {{C_{2b}}} - \sum\limits_{b = 1}^4 {{C_{b2}}} = \left( {0.505 + 0.513 + 0.568} \right) - \\ \;\;\;\;\;\;\left( {0.495 + 0.487 + 0.432} \right) = 0.172, \end{array} $ |
| $ \begin{array}{l} {c_3} = \sum\limits_{b = 1}^4 {{C_{3b}}} - \sum\limits_{b = 1}^4 {{C_{b3}}} = \left( {0.510 + 0.487 + 0.553} \right) - \\ \;\;\;\;\;\;\left( {0.490 + 0.513 + 0.447} \right) = 0.099, \end{array} $ |
| $ \begin{array}{l} {c_4} = \sum\limits_{b = 1}^4 {{C_{4b}}} - \sum\limits_{b = 1}^4 {{C_{b4}}} = \left( {0.439 + 0.432 + 0.447} \right) - \\ \;\;\;\;\;\;\left( {0.561 + 0.568 + 0.553} \right) = - 0.364. \end{array} $ |
同理,将各评价指标的不一致性集合代入式(17),得方案A1相对于方案A2的不满意程度为
| $ {D_{12}} = \frac{{\mathop {\max }\limits_{j \in {D_{ab}}} \left| {{v_{1j}} - {v_{2j}}} \right|}}{{\mathop {\max }\limits_j \left| {{v_{1j}} - {v_{2j}}} \right|}} = \frac{{\left| {0.027 - 0.045} \right|}}{{\left| {0.027 - 0.045} \right|}} = 1. $ |
然后将不一致性指数代入到式(18),得不一致性区间指数矩阵为
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} - &1&1&{0.375}\\ {0.556}& - &{0.688}&{0.304}\\ {0.875}&1& - &{0.583}\\ 1&1&1& - \end{array}} \right]. $ |
根据式(20)可得4个可行装配方案的净劣势值分别为
| $ {d_1} = - 0.056,{d_2} = - 1.453, $ |
| $ {d_3} = - 0.229,{d_4} = 1.737. $ |
根据公式(21), 4个可想装配序列的净优势度分别为
| $ {r_1} = 0.149,{r_2} = 1.625,{r_3} = 0.328,{r_4} = - 1.773. $ |
综上所述,4个可行装配序列的优势值和劣势值如表 5所示.
| 表 5 可行装配序列的优势值、劣势值和净优势度 Table 5 The dominant, inferior values and degree of dominance of feasible assembly sequences |
从表 5可以看出,可行装配序列2具有最大的净优势值,即从16个评价指标的属性出发,该方案对其他方案的优势指标加权之和与其方案相对该方案的优势指标加权之和的差值最大,表明该方案在方案集中的综合优势程度最佳,因此,根据净优势值的排序结果,4个方案优劣对比结果为:2>3>1>4.同理,可行装配序列2具有最小的净劣势值,即该方案对其他方案的劣势指标加权之和与其方案相对该方案的劣势指标加权之和的差值最小,表明该方案在方案集中的综合劣势程度最小,该方案也就最佳,因此,根据净劣势值的排序结果,4个方案的优劣对比结果为:2>3>1>4. 4个方案根据净优势值和净劣势值的排序结果一样,因此,装配序列根据净装配优势度的排序结果为:2>3>1>4.根据该综合评价结果,车间通过反复试装发现,方案2不仅装配效率更高,且装配难度、精度等也较好.最后,方案2被定为装配部门统一装配方案,并指导车间生产,证明了本方法的有效性.
5 结论1) 根据装配序列评估的特点,在调研及专家意见基础上,建立了装配序列评价的指标体系,并提出合理可行的评价公式.
2) 根据各指标属性值及指标间的模糊权重,获取可行装配序列的优势值和劣势值排序,从正面和反面综合优选装配序列,增加了优选结果的准确性.
3) 对某企业产品的传动系统装配方案优选过程进行实例分析,优选出的装配方案得到了该企业认可,证明了该方法的有效性.
4) 其他机构的装配序列评价可根据此模式进行修改,以致对此类装配序列优选提供建议.
| [1] |
RIADH B H, MOEZ T, NIZAR A, et al. Integrated CA-D approach for generating assembly sequence plans based on collision study results[J]. Lecture Notes in Control & Information Sciences, 2015, 78(9): 63-72. DOI:10.1001/978-3-319-17527-0_7 |
| [2] |
VIJAMUKUND R, JOSE M, RAJEEV S, et al. Interactive evaluation of assembly sequences using augmented reality[J]. Teansactions on Robotics and Automation, 1999, 15(3): 435-449. DOI:10.1109/70.768177 |
| [3] |
王孝义, 张友良, 张帆, 等. 装配序列评价研究[J]. 中国机械工程, 2006, 16(13): 1165-1169. WANG Xiaoyi, ZHANG Youliang, ZHANG Fan, et al. Research on evaluating assembly sequences[J]. China Mechanical Engineering, 2006, 16(13): 1165-1169. |
| [4] |
ZHANG Jiayi, HAO Yongping, LIU Ying, et al. A new method of optiaml order reference set for product assembly evaluation[C]//2010 International Conference on Digital Manufacturing & Automation. Zhangjiajie: IEEE Computer Society, 2010, 44: 67-70. DOI: 10.1109/ICDMA.2010.44.
|
| [5] |
袁宝勋, 褚学宁, 李玉鹏, 等. 基于产品设计数据的装配序列定量化评价方法[J]. 计算机集成制造系统, 2014, 20(4): 807-816. YUAN Baovun, CHU Xuening, LI Yupeng, et al. Quanti-taive evaluation approach fou assembly sequences b-ased on product design data[J]. Computer Integrated Manufacturing Systems, 2014, 20(4): 807-816. |
| [6] |
周开俊, 李东波, 许黄敏, 等. 一种产品装配序列评价方法[J]. 计算机集成制造系统, 2006, 12(4): 563-567. ZHOU Kaijun, LI Dongbo, XU Huanmin, et al. Evaluation approach to product assembly sequences[J]. Computer Integrated Manufacturing Systems, 2006, 12(4): 563-567. |
| [7] |
REDDY B, GOTTIPOL U, KALYAN G, et al. A simple and efficient representation for evaluation and selection of assembly sequences[J]. Computer in Industry, 2003, 50(3): 251-264. DOI:10.1016/S0166-3615(03)00015-0 |
| [8] |
LU C, FU H. Evaluation of product assemblability in assembly sequences using the tolerancing approach[J]. International Journal of Production Research, 2006, 44(23): 5037-5063. DOI:10.1080/00207540600579656 |
| [9] |
LI Shiqi, LIU Yi, WANG Junweng, et al. An intelligent interactive approach for assembly process planning b-ased on hierarchical classification of parts[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(9-12): 1903-1914. DOI:10.1007/S00170-013-5426-7 |
| [10] |
李明宇. 复杂产品装配序列规划方法研究[D]. 武汉华中科技大学, 2013: 63-68. LI Mingyu. Research on method of assembly sequen-ce planning for complex product[D]. Wuhan: Huazhong University of Science and Technology, 2013: 63-68. http://cdmd.cnki.com.cn/Article/CDMD-10487-1014024738.htm |
| [11] |
金伟娅, 张康达. 可靠性工程[M]. 北京: 化学工业出版社, 2005: 1-10. JIN Weiya, ZHANG Kangda. Reliability engineering[M]. Beijing: Chemical Industry Press, 2005: 1-10. |
| [12] |
张根保, 葛红玉. GO法在产品装配过程质量分析中的应用[J]. 中国机械工程, 2010, 21(22): 2689-2692. ZhANG Genbao, GE Hongyu. Application and research of GO methodology in quality analysis of product assembly process[J]. China Mechanical Engineering, 2010, 21(22): 2689-2692. |
| [13] |
张吉军. 模糊层次分析法[J]. 模糊系统与数学, 2006, 14(2): 80-88. ZHANG Jijun. Fuzzy analytical hierarchy process[J]. F-uzzy Systems and Mathematics, 2006, 14(2): 80-88. |
| [14] |
METAXIOTIS K, PSARRAS J, SAMOUILIDIS J E, et al. Integrating fuzzy logic into decision support systems:current research and future prospects[J]. Information Management and Computer Security, 2003, 11(2): 53-59. DOI:10.1108/09685220310468592 |
| [15] |
KAHRAMAN C, KAYA I, CEBI S, et al. A comparative analysis for multiattribute selection among renewable energy alternatives using fuzzy axiomatic design and fuzzy analytic hierarchy process[J]. Energy, 2009, 34(10): 1603-1609. DOI:10.1016/j.eswa.2011.01.057 |
| [16] |
CHANG D.Y. Applications of the extent analysis method on fuzzy AHP[J]. European Journal of Operational Research, 1996, 95(3): 649-655. DOI:10.1016/0377-2217(95)00300-2 |
| [17] |
KAYA T, KAHRAMAN C. An integrated fuzzy AHP-ELECTRE methodology for environmental impact as-sessment[J]. Expert Systems with Applications, 2011, 38(7): 8553-8562. DOI:10.1016/j.eswa.2011.01.057 |
| [18] |
MARZOUK M. ELECLTRE Ⅲ model for value engineering application[J]. Automation in Construction, 2010, 20(5): 596-600. DOI:10.1016/J.AUTCON.2010.11.026 |
| [19] |
张俊. 基于ELECTRE法与熵权法的施工模板配板方案优选技术研究[D]. 天津: 河北工业大学, 2014: 30-36. ZHANG Jun. Template matching board construction s-cheme optimization technology research based on the method of ELECTRE and entropy weight[D]. Tianjin: Heibei University of Technology, 2014: 30-36. http://cdmd.cnki.com.cn/Article/CDMD-10080-1015998419.htm |
 2018, Vol. 50
2018, Vol. 50



