2. 中国舰船研究设计中心,武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
齿轮的磨损会造成接触环境恶化,加大齿间动态载荷,而载荷的增大又会加重齿轮磨损,磨损会造成更严重的轮齿失效形式.揭示磨损与齿轮参数的关系可实现主动抑制磨损,降低齿轮的振动冲击,延长齿轮使用寿命.
目前,各类齿轮系统磨损机理的研究还不尽完善,加之齿轮的啮合及运动学参数复杂,很难建立起磨损与齿轮参数间的直接关系.以往的研究中给定齿轮参数后,都是通过确定啮合载荷和齿面滑动距离(速度)后,应用磨损机理来确定磨损量.在对齿轮磨损的数值计算中,国内外学者普遍采用Archard磨损模型[1-5],只是在确定齿轮的啮合载荷和齿面滑动距离时方法不尽相同,Anddersson[1]通过齿轮几何学理论得到了啮合过程中滑动距离与啮合位置的关系. Flodin等[2]通过单点观测法确定了滑动速度和啮合压力. Wu等[3]在考虑了齿轮动力学和弹性流体动力润滑的影响下,推导了齿轮磨损计算公式.王晓笋等[4]和Kuang等[5]研究了齿面累积磨损量对轮齿啮合刚度的影响并进行了动力学分析.上述模型的齿间载荷只是进行了简单处理,并未考虑磨损带来的间隙对载荷的影响.
磨损是一个逐渐累积的渐变过程,达到极限值的时间历程很长,为了保证足够精度,数值仿真的方法给定的模拟步长又不能太大,这两个因素都会导致进行一次磨损量计算将耗费大量的时间,为了建立磨损与齿轮参数的关系,需要进行大样本模拟,若参数样本较多时,这种数值仿真算法将不再适用.
为了解决上述问题,可以使用近似模型来代替磨损数值模型.常用的近似逼近方法有响应面方法[6]、自适应神经网络方法[7]、Kriging方法[8]、径向基方法[9]等.响应面模型构造的函数形式固定,不适合解决复杂问题,自适应神经网络的稳健性低,同样精确度时的计算效率不如Kriging模型. Laurenceau等[10]将Kriging模型用在飞机动力学设计中,并与响应面法进行了对比. Lucifredi等[11]将动态Kriging模型应用于水电力系统的预测维护中,并对比了它与神经网络方法的计算精度与效率.本文采用Kriging方法对齿面磨损进行预测,用Kriging模型代替磨损仿真模型.
1 齿面磨损模型齿轮在高接触压力的作用下,相互啮合的轮齿表面发生相对滚动和滑动.虽然大部分齿轮采用了油脂润滑,但是润滑状态还是处于边界润滑或混合润滑,啮合表面不能被润滑剂完全隔开,摩擦表面会产生金属间的直接摩擦.此时,相互啮合的轮齿表面在低速重载作用下,会形成材料的转移以及表层金属剥落,造成齿轮的磨损.
Flodin等[2]基于广义的Archard磨损方程提出了直齿轮轻微磨损预测模型.假定在极短的时间内,齿廓上的点i的表面压力pi和滑移速度vi保持不变.因此,点i的磨损量可表示为
| $ {{h}_{i, n}}={{h}_{i, n-1}}+\Delta tkN\sum\limits_{j=1}^{s}{{{p}_{i, j}}{{v}_{i, j}}}. $ |
式中:hi, n为啮合点i处n次磨损后的磨损深度,hi, n-1为啮合点i处n-1次磨损后的磨损深度,n为当前磨损次数,Δt为时间步长,k为磨损系数,N为每次磨损运行间隔的转数,在此期间齿轮轮廓将不进行更新,s为赫兹接触半径内的点. pi, j为在j点接触时i点的表面压力,vi, j为点i的滑移速度.
1.1 表面压力基于Winkler弹性模型可得到在啮合点j接触时处于接触半径内齿廓点i的表面压力pi, j:
| $ {{p}_{i, j}}({{x}_{i, j}})=\frac{(0.59{{E}^{*}})}{Ra}({{a}^{2}}-x_{i, j}^{2}). $ | (1) |
式中:j为啮合点,a为接触半径,xi, j为接触半径内的一点i到啮合点j的距离,E*为等效弹性模量,R为两个圆柱的综合曲率半径.式(1)中的间接变量计算公式为
| $ a={{\left( \frac{4WR}{\mathsf{ π} {{E}^{*}}}~ \right)}^{1/2}}. $ |
式中:W为W1或W2,W1为第一对轮齿啮合副分担的法向力,W2为第二对轮齿啮合副分担的法向力,由式(2)和式(3)确定,当第1对齿轮先接触时,有
| $ \left\{ \begin{align} &{{W}_{1}}=\frac{{{k}_{1}}\left( t \right)\left( F+\left| \mathit{\Delta } \right|\cdot {{k}_{2}}\left( t \right) \right)\text{ }}{{{k}_{1}}\left( t \right)+{{k}_{2}}\left( t \right)}, \\ &{{W}_{2}}=\frac{{{k}_{2}}\left( t \right)\left( F-\left| \mathit{\Delta } \right|\cdot {{k}_{1}}\left( t \right) \right)}{{{k}_{1}}\left( t \right)+{{k}_{2}}\left( t \right)}. \\ \end{align} \right. $ | (2) |
当第2对齿轮先接触时,
| $ ~\left\{ \begin{align} &{{W}_{1}}=\frac{{{k}_{1}}\left( t \right)\left( F-\left| \mathit{\Delta } \right|\cdot {{k}_{2}}\left( t \right) \right)}{{{k}_{1}}\left( t \right)+{{k}_{2}}\left( t \right)}\text{, } \\ &{{W}_{2}}=\frac{{{k}_{2}}\left( t \right)\left( F+\left| \mathit{\Delta } \right|\cdot {{k}_{1}}\left( t \right) \right)}{{{k}_{1}}\left( t \right)+{{k}_{2}}\left( t \right)}. \\ \end{align} \right. $ | (3) |
式中:F为单位宽度的法向总载荷,k1(t)和k2(t)为齿对1和齿对2单位齿宽的啮合刚度. Δ为齿轮的几何侧隙.
当啮合点在B1C段时,
| $ \left| \mathit{\Delta } \right|=\left| {{h}_{1}}\left( y \right)+{{h}_{2}}\left( y \right)-\left( {{h}_{1}}\left( y+{{p}_{\text{b}}} \right)+{{h}_{2}}\left( y+pb \right) \right) \right|; $ |
当啮合点在DB2段时,
| $ \left| \mathit{\Delta } \right|=\left| {{h}_{1}}\left( y \right)+{{h}_{2}}\left( y \right)-\left( {{h}_{1}}\left( y-{{p}_{\text{b}}} \right)+{{h}_{2}}\left( y-{{p}_{\text{b}}} \right) \right) \right|. $ |
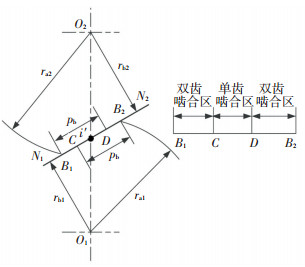
如图 1所示,y为接触点i和节点i’沿着啮合线的距离,h(y)为磨损深度.
|
图 1 齿轮啮合关系 Figure 1 Meshing relation plot of gears |
应用齿轮啮合理论可确定点i的滑动速度:
| $ \begin{align} &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{v}_{i}}=\left( {{\omega }_{1}}+{{\omega }_{2}} \right)\times {{y}_{i}}, \\ &{{y}_{i}}=i{{i}^{\prime }}={{r}_{\text{b1}}}\left( \text{tan}\ {{\beta }_{1i}}-\text{tan}\ \phi \right)={{r}_{\text{b2}}}(\text{tan}\ \phi -\text{tan}\ {{\beta }_{2i}}). \\ \end{align} $ |
式中:rb1rb2为主从动轮的基圆半径,β1iβ2i分别为啮合点i在齿轮1和齿轮2上对应的压力角,ϕ为啮合角.
2 Kriging预测模型上述磨损模型的工作参数、尺寸参数均是确定的,属于确定性模型.当N=1 000转,磨损次数为450时,计算时间大约为1 h,若给定另一组参数,程序需要重新计算并消耗同样的时间.在大量样本面前,直接计算的方法将不再适用,采用Kriging模型可以建立响应与模型参数的关系,当给定样本后可以快速精确地预测出磨损量(响应值).
同时,磨损是一个逐渐累积的过程,当磨损量达到极限时,齿轮失效,由齿面磨损的计算公式可以看出,在计算过程中假定了在N转内齿廓不进行更新,如果N的取值太大会造成计算精度低,因此在允许的范围内使N的取值尽可能小,但会造成计算时间长.在Kriging模型中将时间参数考虑进去,可以快速精确地预测磨损的变化趋势.
Kriging模型将模型参数看成随机变量,将磨损量看成随机响应,并将随机响应模型描述为两部分,参数化的线性回归模型和非参数化的随机过程模型.为了满足模拟过程的无偏性,可得随机响应的估计值为
| $ \mathit{\boldsymbol{\hat h}}\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{f}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}{\mathit{\boldsymbol{\beta }}^ * } + \mathit{\boldsymbol{r}}{\left( \mathit{\boldsymbol{x}} \right)^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{\beta }} ^ * }). $ | (4) |
式中:x={x1, x2, …, xn+1}为待测点,n+1为变量数;f(x)T={f1(x), f2(x), …, fp(x)}为向量x的多项式,p为多项式数;β*={β1*, β2*, …, βp*}T为模拟的广义最小二乘估计;假设有m个样本,分别为xs1, xs2, …, xsm;r(x)={R(θk, x, xs1), R(θk, x, xs2), …, R(θk, x, xsm)}T为待测点x和样本xs1, xs2, …, xsm之间的相关向量;Rm×m为样本间的相关矩阵;H为响应样本值;F为样本的多项式;β*为模拟的最小二乘估计,
| $ {\mathit{\boldsymbol{\beta }}^ * } = {\left( {{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{F}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{Y}}. $ |
式中:R(θk, xi, xj)是样本点中任意两个样本点xi和xj的空间相关方程,i, j∈s1, …, sm由用户自定义,其中计算效果最好,被广泛采用的是高斯相关方程.
| $ R({\theta _k}, {\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}) = \prod\limits_k^{n + 1} {{\rm{exp}}( - {\theta _k}\left| {x_k^i - x_k^j} \right|{^2})} . $ |
由R(θk, xi, xj)可组集为相关矩阵
| $ \mathit{\boldsymbol{R = }}{\left[{\begin{array}{*{20}{c}} {\sigma _1^2}&{R\left( {{\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{x}}_2}} \right)}& \cdots &{R\left( {{\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{x}}_m}} \right)}\\ {R\left( {{\mathit{\boldsymbol{x}}_2}, {\mathit{\boldsymbol{x}}_1}} \right)}&{\sigma _2^2}&{}&{}\\ \vdots &{}&{}&{}\\ {R\left( {{\mathit{\boldsymbol{x}}_m}, {\mathit{\boldsymbol{x}}_1}} \right)}&{}&{}&{\sigma _m^2} \end{array}} \right]_{\left( {m \times m} \right).}} $ |
应用最大似然估计法可得到相关方程中θT={θ1, …, θk, …, θn+1}T的最优解θ*为
| ${\mathit{\boldsymbol{\theta }}^ * } = \mathop {{\rm{min}}}\limits_\theta \left\{ {{{\left| \mathit{\boldsymbol{R}} \right|}^{\frac{1}{m}}}{\sigma ^2}} \right\}. $ |
式中, m为样本数,|R|为相关矩阵R的行列式.
当样本给定后,可确定出β*、R、H、F的具体表达式,当给出待测点x以及f(x)的回归模型,以及r(x)的相关方程,即可通过式(4)得到
表 1为计算一对齿轮磨损需要的参数,材料为45号钢.齿轮尺寸参数、工作参数和磨损参数均参考自文献[2].虽然文献[2]只进行了理论分析,但是被大量学者认可,并在文献[12]中进行了实验验证.
| 表 1 齿轮参数 Table 1 Parameters of gear pair |
定义磨损次数为150次,从第n-1次磨损到第n次磨损之间,齿轮转过了N=1 000转,并且1, 2, …, N转的任意一转中,齿轮的轮廓是恒定的,啮合点的压力和速度都相等.
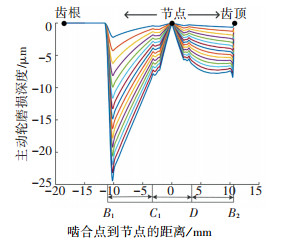
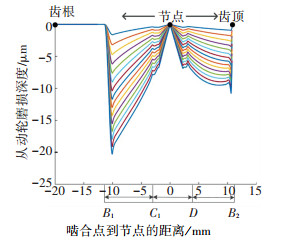
由图 2和图 3可知,节点处的磨损最小,齿根处的磨损要大于齿顶的磨损,主动轮(小齿轮)的磨损大于从动轮(大齿轮)的磨损,这与参考文献[12-14]得到的结论一致.最大磨损出现在主动轮齿廓点233处和从动轮263处.如图 1所示,一对齿的啮合从B1开始至B2结束,最大磨损出现在啮入位置和啮出位置处.由图 2和图 3可知,由于考虑间隙的影响,在单双齿啮合转换处,磨损量出现先增大再减小的现象,不同于文献[2]中的一直减小的趋势.
|
图 2 n次磨损后主动轮磨损深度(n=10, 20, ……, 150) Figure 2 Wear depth of the pinion after n wear cycles |
|
图 3 n次磨损后从动轮磨损深度(n=10, 20, ……, 150) Figure 3 Wear depth of the driven gear after n wear cycles |
若齿形角αn、齿宽b、外加力矩T1、小齿轮速度n1以及磨损系数k为变量,时间t为1 000 min,采用拉丁超立方试验设计方法,分别得到变量和真实磨损组成的样本50、100、500组,建立3种不同样本量下的Kriging近似模型(用Kriging-50,Kriging-100,Kriging-500表示).回归模型中多项式p=0,相关模型为高斯方程. 3种Kriging模型的具体参数如表 2所示.
| 表 2 Kriging模型中相关参数 Table 2 Parameters of the three Kriging models |
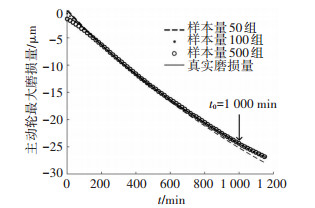
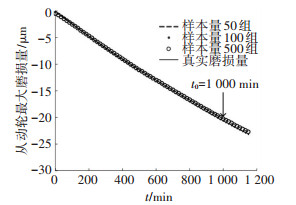
图 4、5为齿轮最大磨损量变化曲线,由图 4、5可知,磨损量随时间逐渐累积增加.在样本量为50、100和500时,建立Kriging模型的时间只需几秒钟,并且模型对真实磨损量的逼近精度很高,同时,真实磨损量只提供了t0时间内的样本,Kriging模型可预测t>t0时的磨损量,并且在样本量为100组以上时,误差非常小.
|
图 4 主动轮不同样本量时Kriging模型的模拟精度对比 Figure 4 Simulation precision with different Kriging model of pinion gear |
|
图 5 从动轮不同样本量时Kriging模型的模拟精度对比 Figure 5 Simulation precision with different Kriging model of driven gear |
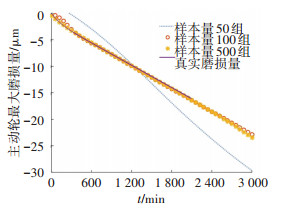
为说明Kriging模型的优越性,本文同时采用人工神经网络模型(ANN)[15],建立了6-13-1形式的3层BP神经网络,隐含层的传递函数选用S型对数函数,输出层的传递函数选用purelin线性传递函数,训练函数选择trainlm函数,网络的训练误差达到10-6时结果收敛. 图 6、7为不同样本量时ANN模型的模拟精度.
|
图 6 主动轮不同样本量时ANN模型的模拟精度对比 Figure 6 Simulation precision with different ANN model of pinion gear |
|
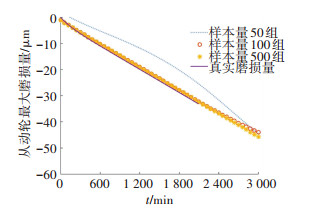
图 7 从动轮不同样本量时ANN模型的模拟精度对比 Figure 7 Simulation precision with different ANN model of driven gear |
采用50组样本训练得到的ANN模型的精确程度不高,采用100、500组的模型精确程度都很高,并且对未来趋势的预测也比较准确.同样采用50、100和500组样本建立的Kriging近似模型,3个Kriging模型的精确程度都很高,对未来趋势的预测也比较准确.由此可看出,与ANN方法相比,Kriging方法可使用更少的样本得到较高的精度.
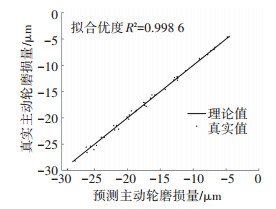
为了检验模型的通用性,另外取50组样本分别带入上述3种Kriging模型进行检验,将样本的真实值与Kriging模型的预测值进行对比,结果表明Kriging-50模型的拟合优度为0.764 5,Kriging-100模型的拟合优度为0.998 6,Kriging-500模型的拟合优度为0.999 9,可见当采用Kriging-100模型进行检验时,拟合优度可近似达到1,因此,只需要100组样本模拟得到的Kriging模型可近似代替磨损预测模型. 图 8为采用Kriging-100模型的磨损量预测值和真实值.
|
图 8 基于Kriging的预测值与真实值 Figure 8 Prediction and actual wear depth based on Kriging model |
样本量为105时,采用Kriging模型进行磨损量预测所需要的时间只有几秒钟,而用磨损仿真模型需要3.8年.可以看出,采用Kriging模型比直接采用磨损预测模型大大节约了时间和成本.
4 结论本文考虑了磨损对齿廓表面几何形状的影响,推导了几何侧隙下的齿间载荷分配公式,并以此为基础,引入Archard磨损模型和Winkler弹性力学模型,建立了低速重载齿轮的磨损量计算模型.基于Kriging方法得到了近似逼近模型,建立了齿轮参数与磨损的直接关系.为减少齿轮振动冲击提供了途径.得到的结论如下:
1) 节点处的磨损最小,齿根处的磨损要大于齿顶的磨损,主动轮(小齿轮)的磨损大于从动轮(大齿轮)的磨损.
2) 节点到齿顶的磨损分布较均匀,而齿根到节点的磨损变化较剧烈.重点应该关注齿根附近的磨损.
3) 使用很少的样本建立的Kriging模型可以完全代替磨损数值模型,计算效率和拟合优度都非常高.可用于对未知磨损的预测.
| [1] |
ANDERSSON S. Partial EHD theory and initial wear of gears[D]. Stockholm: Royal Institute of Technology, 1975.
|
| [2] |
FLODIN A, ANDERSSON S. Simulation of mild wear in spur gears[J]. Wear, 1997, 207(1/2): 16-23. DOI:10.1016/S0043-1648(96)07467-4 |
| [3] |
WU S, CHENG H S. Sliding wear calculation in spur gears[J]. Journal of Tribology, 1993, 115(3): 493-500. DOI:10.1115/1.2921665 |
| [4] |
王晓笋, 巫世晶, 周旭辉, 等. 含磨损故障的齿轮传动系统非线性动力学特性[J]. 振动与冲击, 2013, 32(16): 37-43, 69. WANG Xiaosun, WU Shijing, ZHOU Xuhui, et al. Nonlinear dynamics analysis of gear transmission system with wear fault[J]. Journal of Vibration and Shock, 2013, 32(16): 37-43, 69. DOI:10.3969/j.issn.1000-3835.2013.16.007 |
| [5] |
KUANG J H, LIN A D. The effect of tooth wear on the vibration spectrum of a spur gear pair[J]. Journal of Vibration and Acoustics, 2001, 123(3): 311-317. DOI:10.1115/1.1379371 |
| [6] |
CHENG J, LI Q S. Application of the response surface methods to solve inverse reliability problems with implicit response functions[J]. Computational Mechanics, 2009, 43(4): 451-459. DOI:10.1007/s00466-008-0320-0 |
| [7] |
PAPADRAKAKIS M, LAGAROS N D. Reliability-based structural optimization using neural networks and Monte Carlo simulation[J]. Computer Methods in Applied Mechanics and Engineering, 2002, 191(32): 3491-3507. DOI:10.1016/s0045-7825(02)00287-6 |
| [8] |
ZHU Z F, DU X P. Reliability analysis with Monte Carlo simulation and dependent kriging predictions[J]. Journal of Mechanical Design, 2016, 138(12): 121403. DOI:10.1115/1.4034219 |
| [9] |
TAN X H, BI W H, HOU X L, et al. Reliability analysis using radial basis function networks and support vector machines[J]. Computers and Geotechnics, 2011, 38(2): 178-186. DOI:10.1016/j.compgeo.2010.11.002 |
| [10] |
LAURENCEAU J, SAGAUT P. Building efficient response surfaces of aerodynamic functions with kriging and cokriging[J]. Aiaa Journal, 2008, 46(2): 498-507. DOI:10.2514/1.32308 |
| [11] |
LUCIFREDI A, MAZZIERI C, ROSSI M. Application of multiregressive linear models, dynamic kriging models and neural network models to predictive maintenance of hydroelectric power systems[J]. Mechanical Systems and Signal Processing, 2000, 14(3): 471-494. DOI:10.1006/mssp.1999.1257 |
| [12] |
FLODIN A. Wear Investigation of Spur gear teeth[J]. Tribotest journal, 2000, 7(1): 45-60. DOI:10.1002/tt.3020070106 |
| [13] |
AMARNATH M, SUJATHA C, SWARNAMANI S. Experimental studies on the effects of reduction in gear tooth stiffness and lubricant film thickness in a spur geared system[J]. Tribology International, 2009, 42(2): 340-352. DOI:10.1016/j.triboint.2008.07.008 |
| [14] |
王淑仁, 闫玉涛, 丁津原. 渐开线直齿圆柱齿轮啮合磨损试验研究[J]. 东北大学学报(自然科学版), 2004, 25(2): 146-149. WANG Shuren, YAN Yutao, DING Jinyuan. Experimental study on mesh-wear of involute spur gears[J]. Journal of Northeastern University(Natural Science), 2004, 25(2): 146-149. |
| [15] |
朱丽莎, 张义民, 卢昊, 等. 基于神经网络的转子振动可靠性灵敏度分析[J]. 计算机集成制造系统, 2012, 18(1): 149-155. ZHU Lisha, ZHANG Yimin, LU Hao, et al. Reliability sensitivity analysis of rotor vibration based on neural network[J]. Computer Integrated Manufacturing Systems, 2012, 18(1): 149-155. |
 2018, Vol. 50
2018, Vol. 50


