气体绝缘输电线路(gas-insulated transmission lines,GIL)具有电压等级高、输送容量大、电能损耗低、电磁干扰小等优点,且在传统架空线路受约束的区域,如需要跨越海峡、大江等条件下具有巨大的优势,因此GIL得到广泛的应用.在运行过程中,由于焦耳热损耗,输电线路一直处于发热状态,导致线路温度升高.温升不仅降低了线路的最大载流能力,使输电管道发生热变形,而且温度超过一定限度时将影响线路内部非导电材料的绝缘性能,使GIL内部绝缘气体如SF6分解,降低线路使用寿命,甚至发生严重的放电事故.因此温度是检验GIL运行状况是否良好的重要指标,通常的热检测手段只能测量外壳表面温度,难以掌握内部设备如导体、绝缘支柱、密封圈、触头等的温升程度.通过理论研究GIL的热特性,从而确定不同运行条件下内部设备的发热状态及其与外壳之间的温差,可为GIL过热状态监测提供技术支持,并为GIL的热可靠性设计提供理论参考.
目前,GIL热特性的研究还不够广泛.实验研究方面,Minaguchi等[1]测试了不同单相单元的温升特性,分别测试了在不同负载电流、绝缘气体压力、表面发射率情况下的稳态温升及考虑太阳辐射及风速时的暂态温升特性,并提出了一种GIL温度计算方法. Cookson等[2]对长为6.1 m,电压等级为120 kV的气体绝缘输电线路的单元进行了试验研究,比较了不同气体压力、气体种类对GIL线路的温升影响. Xing等[3]采用氟碳气体替代SF6气体,测试了GIL外壳和导体的温度,并计算气体的传热系数,然后计算了实际情况下的GIL温度,并将计算结果与试验结果进行了对比.
在理论分析计算方面,常用的方法有解析法和有限元法.解析法通过建立焦耳热损耗与对流换热以及热辐射的热平衡关系迭代求解出导体与外壳温度[4-7].该方法只能用于稳态温升的近似初步计算,且不能反映GIL整体温度分布.有限元法通过建立电磁场、流场、温度场等多物理场耦合模型的方法进行GIL线路温升计算. Kim S W等[8]以及Kim J K等[9]建立了有限元模型,但模型不包括流体域,用量纲一参数计算外壳的对流换热系数,计算时设置热通量为常数,虽可简化计算,但可能与物理实际不符.吴晓文等[10]、Novák等[11]建立了包含绝缘气体及外部空气域的二维多物理场耦合有限元模型,避免了在固体表面施加热边界条件,且考虑了温度相关的气体热物性参数,降低了计算误差.王健等[12]建立了不包含壳外空气流体域的三维多物理场耦合模型,同时进行了GIL热致伸缩形变的计算,并结合实验数据进行了模型准确性的验证.由于不同类型GIL的几何结构、材质和有限元方法的假定条件及设置边界条件的差异,GIL的热特性差异很大.
本文假定GIL内部绝缘气体为自然对流状态,并采用了温度相关的气体热物性参数,考虑外壳的电感效应和阻抗的温度效应,发展了含外部空气域GIL热特性的三维气热耦合有限元数值计算方法.基于Minaguchi等[1]的实验数据,对该有限元理论计算方法进行了验证分析.根据苏通GIL管廊工程的运行工况特点,以某国产1 000 kV的GIL产品为研究对象,分析了不同空气流速、运行电流、环境温度、绝缘气体压强、表面发射率等对该GIL热特性的影响.
1 三维气热耦合有限元数值计算方法 1.1 计算模型及基本控制方程在GIL内部充满绝缘气体,由于导体内存在负载电流和外壳内存在感应电流,势必会产生焦耳热损耗.而导体产生的热量一方面通过辐射散发,同时与绝缘气体存在热量交换.外壳内表面吸收辐射热量,同时与绝缘气体进行热量交换,而外壳的外表面通过辐射把热量散发给周围环境,同时与周围空气进行对流换热.可见GIL的热量传递过程综合了对流、热传导及辐射3种换热方式,由此建立计算模型需要能够反映这一复杂综合传热过程.本文的计算模型如图 1所示,该模型的流体域有GIL外部的空气域和内部的绝缘气体域,固体域为具有一定厚度的外壳和导体.固体域和流体域通过设定流固耦合交接面来传输温度和热流量.
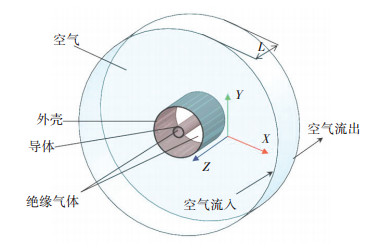
|
图 1 计算模型 Figure 1 Simulation model |
该模型假设条件为:1)计算时不考虑太阳辐射对温升的影响;2)模型将气固交界面进行耦合,考虑气体表面之间的辐射,但由于气体对辐射的吸收及反射能力很差,所以忽略气体对辐射热量的吸收;3)绝缘气体采用SF6,其与空气的热物性参数如密度、黏度及导热系数均与温度相关,是温度的函数;4)空气层外边界温度为远场周围环境温度,不受GIL发热影响;5)导体及外壳内材质各向同性,热损耗在其内部均匀分布.
通常有限元计算方法中在外壳外表面施加外壳周围空气自然对流引起的热流量,热流量的大小有很多经验关系式,这势必会带来热特性计算结果的差异.因此,本文发展的计算方法在GIL外部区域建立足够大空间的空气域,给定空气域径向周围边界的固定温度来代表外界环境的温度.在GIL内部,不同位置的绝缘气体因温度不同而导致不同位置的气体密度不同,从而引起自然对流.在GIL外部,当环境为无风速条件时,外界空气因相同原因形成自然对流;当考虑环境为有风速时,空气流动为强制流动.对流换热则根据气体的流动状态不同而有不同的求解方式.流体域的换热控制方程由质量守恒方程、动量守恒方程及能量守恒方程构成[13]:
质量守恒方程
| $ \frac{{\partial {\rho _{\rm{f}}}}}{{\partial t}} + {\rho _{\rm{f}}}\nabla \cdot v = 0, $ |
动量守恒方程
| $ {\rho _{\rm{f}}}\left( {\frac{{\partial v}}{{\partial t}} + v \cdot \nabla v} \right) = {\eta _{\rm{f}}}{\nabla ^2}v + E, $ |
能量守恒方程
| $ {\rho _{\rm{f}}}{c_p}\left( {\frac{{\partial T}}{{\partial t}} + v \cdot \nabla T} \right) = {\lambda _{\rm{f}}}{\nabla ^2}T. $ |
式中:ρf为空气或绝缘气体密度,kg/m3;t为时间,s;v为气流速度,m/s;ηf为气体动力黏度,Pa·s;E为动量方程的广义源项;cp为比热容,J/(kg·K);T为绝对温度,K;λf为气体导热系数,W/(m·K).
气体热物性参数包括密度、黏度、导热系数, 与温度的关系如下[10]:
| $ \rho \left( T \right) = \frac{{{\rho _0}{T_0}}}{T}, $ |
| $ \lambda \left( T \right) = {\lambda _0}{\left( {\frac{T}{{{T_0}}}} \right)^{1.5}}\frac{{{T_0} + S}}{{T + S}}, $ |
| $ \eta \left( T \right) = {\eta _0}{\left( {\frac{T}{{{T_0}}}} \right)^{1.5}}\frac{{{T_0} + S}}{{T + S}}. $ |
式中:λ0、η0分别为0 ℃时气体的导热系数及动力黏度;T0为参考温度,273 K;S为Sutherland常数,K.
在模型中,通过设置气体域浮力项来考虑自然对流的作用,浮力项中需设置重力大小及方向以及气体的参考密度.在重力的作用下,由于密度的差异产生浮力,当考虑浮力时,基于流体密度和参考密度的差异,在动量方程中将添加一个源项:
| $ E=\left( {{\rho _{\rm{f}}} - {\rho _{\rm{r}}}} \right)g, $ |
动量方程变为
| $ {\rho _{\rm{f}}}\left( {\frac{{\partial v}}{{\partial t}} + v \cdot \nabla v} \right) = {\eta _{\rm{f}}}{\nabla ^2}v + \left( {{\rho _{\rm{f}}} - {\rho _{\rm{r}}}} \right)g. $ |
式中:ρr为参考密度,kg/m3;g为重力加速度,kg·m/s2.选择环境温度下气体的密度为参考密度,密度不等于ρr的流体将被作用一个或正或负的浮力.自然对流条件下,绝缘气体域选用层流模型,气体域端面设置为对称边界;空气气体域也选用层流模型,气体域端面设置为开口边界.
为了保证GIL的运行安全性,一般需要采用风机通风来保证廊管内气流的畅通,这样GIL壳外气流并不是自然对流状态,而是强制流动状态.基于外壳直径和运行过程中的空气流速范围(>1 m/s),通过计算雷诺数可知, 当使用风机通风时,外部气流处于湍流状态, 此时,空气气体域选用k-ε湍流模型,气体端面设置速度入口及压力出口边界,空气流速根据运行条件进行选择.
GIL导体与外壳内部的热量传递通过热传导方式进行,内部导热微分控制方程为[10]
| $ {\rho _{\rm{s}}} = {c_p}\frac{{\partial T}}{{\partial t}} = {\lambda _{\rm{s}}}{\nabla ^2}T + Q. $ |
式中:ρs为导体或外壳的密度,kg/m3;λs为导体或外壳的导热率,W/(m·K);Q为热损耗,J.
辐射换热量与温度及表面性质有关.两个不同表面单元之间的辐射换热量表达式为[14-15]:
| $ {Q_i} = \frac{1}{{\frac{{1 - {\varepsilon _i}}}{{{A_i}{\varepsilon _i}}} + \frac{1}{{{A_i}{F_{ij}}}} + \frac{{1 - {\varepsilon _j}}}{{{A_j}{\varepsilon _j}}}}}\sigma \left( {T_i^4 - T_j^4} \right), $ |
| $ {F_{ij}} = \frac{1}{{{A_i}}}\iint\limits_{{A_i}{A_j}} {\frac{{\cos {\theta _i}\cos {\theta _j}}}{{\mathsf{ π}{r^2}}}{\text{d}}{A_i}{\text{d}}{A_j}}, $ |
式中:ε为表面发射率,Ai、Aj为单元i与j的面积,Fij为角系数,σ为史蒂芬玻尔兹曼常数,θi、θj为单元Ai与Aj的法线与二者连线的夹角,r为单元i与j之间的距离.辐射边界条件通过设置气体域上的气固耦合面的表面发射率来考虑,同时考虑到气体发射和吸收辐射的能力,气体被视为辐射透明体.
由于外壳的屏蔽作用,GIL导体可不考虑邻近效应的影响,只需考虑集肤效应的影响,导体及外壳电阻可用以下公式[16]计算:
| $ {R_{\rm{i}}} = {K_{\rm{f}}}\frac{{{\rho _{20}}\left[ {1 + {\alpha _{20}}\left( {{T_{\rm{m}}} - 20} \right.} \right]}}{{{S_{\rm{i}}}}}. $ |
式中:Ri为导体或外壳电阻,Ω/m;Kf为集肤效应系数;ρ20为20 ℃时导体或外壳的直流电阻率,Ω·m;α20为电阻温度系数,1/℃;Tm为导体或外壳的运行温度,℃;Si为导体或外壳的横截面积,mm2.
由于外壳电流与导体电流方向相反,相当于电流从远处返回,故导体圆管内的电磁场可看作独立的,不受外壳电流影响,其集肤效应系数计算与圆管计算公式一致,即
| $ \begin{array}{*{20}{c}} {{K_{\rm{f}}} = 1 + 0.03{{\left\{ {\frac{{\left[ {1 - 0.0016\left( {{T_{\rm{m}}} - 75} \right)} \right]C}}{{10}}} \right\}}^{3.75}} \times }\\ {{{\left\{ { - \frac{{\left[ {1 - 0.0016\left( {{T_{\rm{m}}} - 75} \right)} \right]C}}{D}} \right\}}^{1.5}},} \end{array} $ |
式中:C为导体或外壳壁厚,mm;D为导体或外壳的外径,mm.
导体或外壳横截面积为
| $ {S_{\rm{i}}} = {\rm{ \mathsf{ π} }}\left( {D - C} \right)C, $ |
导体每米损耗为
| $ {P_{\rm{C}}} = I_{\rm{C}}^2{R_{\rm{C}}}. $ |
式中:PC为导体每米损耗,W/m;IC为GIL额定电流,A;RC为导体电阻,Ω/m.
则导体单位体积发热功率为
| $ {P_{{\rm{CV}}}} = \frac{{{P_{\rm{C}}}}}{{{S_{\rm{C}}}}} \times {10^6}, $ |
式中PCV为导体单位体积发热功率,W/m3.
外壳每米损耗为
| $ {P_{\rm{T}}} = I_{\rm{T}}^2{R_{\rm{T}}}. $ |
式中:PT为外壳每米损耗,W/m;IT为外壳感应电流,A.一般当GIL长度<20 m时,可取IT=0.95 IC,当GIL长度>20 m时,可取IT=IC;RT为导体电阻,Ω/m.
则外壳单位体积发热功率为
| $ {P_{{\rm{TV}}}} = \frac{{{P_{\rm{T}}}}}{{{S_{\rm{T}}}}} \times {10^6}. $ |
式中PTV为导体单位体积发热功率,W/m3.
将导体与外壳的发热功率作为激励施加在模型中作为热源.
1.2 温度场计算结果与实验结果对比分析本文以Minaguchi等[1]实验中5 600 A GIL为研究对象,其结构如图 2所示.
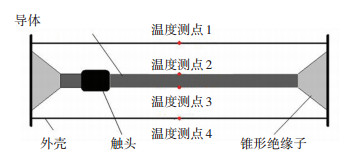
|
图 2 实验GIL结构及温度测点位置 Figure 2 Experimental structure of GIL and the locations of temperature measurement points |
实验过程中的温度测点除了图 2中所示外,在图中测点两侧相隔一定距离各另有4个同样布置的测点.实验发现, 相同位置的测点所测得的温度是相同的,可以认为在该实验条件下GIL的轴向温度分布是均匀的.所以可以用图 1所示计算模型进行温度场计算,得到的温度场分布可以代表整体温度场分布,计算模型中L=100 mm.
Minaguchi等[1]以此结构进行了3组不同运行条件下的实验, 以研究GIL温升特性,导体与外壳均为铝合金材料,材料型号与参数见表 1.
| 表 1 实验GIL材料及尺寸参数 Table 1 Material and size parameters of GIL in the experiment |
采用本文模型分别对3种运行条件进行仿真计算,得到的计算值与实验值的对比结果见表 2.
| 表 2 温度场计算值与实验值对比 Table 2 Comparison between the calculated and tested results of temperature field |
从表 2对比结果可以看出,最大误差出现在运行条件为5 600 A,24 ℃条件下测点一处的温度,误差为2.13%,整体误差均较小,且测点4温度仿真结果与实验结果完全一致,所以使用本模型进行GIL温度场仿真计算是可以得到较准确的温度场分布的.
以上分析验证了本模型进行GIL温度场计算的有效性.本文根据苏通GIL综合管廊工程的运行工况特点,以某国产1 000 kV的GIL产品[17]为研究对象,分析了主要影响参数对该GIL热特性的影响.
2 GIL热特性计算结果及其分析在GIL运行中,对导体及外壳的温度有严格的要求,因为温度不仅影响GIL的最大载流能力,而且对于GIL的安全运行有着重大影响.本文主要考虑了空气流速、负载电流、环境温度、绝缘气体压强、表面发射率这5个主要因素对于GIL运行温度的影响.假定的基本额定计算工况见表 3,本文对上述不同影响因素进行了多次仿真计算.
| 表 3 基本工况的计算条件 Table 3 Basic simulation conditions |
项目中的某国产1 000 kV的GIL材料及尺寸参数见表 4,建立的有限元模型如图 1所示,计算模型中L=1 m.
| 表 4 项目GIL材料及尺寸参数 Table 4 Material and size parameters of GIL in the project |
计算网格采用多块化的结构化网格,在气体区域气体与固体交界面附近进行了网格加密,综合考虑了计算效率与准确性,对空气区域的网格划分较粗大,绝缘气体网格划分较细密.本文选择了多种不同数目的网格,经计算发现,当网格数超过本文采用的网格数265 000后,GIL温度的变化不超过1%,因此视为所选网格数下的计算结果具有网格无关性.
2.1 假定基本工况下GIL的热特性分析基本额定工况下温度计算结果如表 5所示,表中给出了GIL的温度极值和整体平均值. 图 3为基本工况下GIL温度、流速分布图.可以看到,在管道径向,由于导体温度高于外壳温度,这样绝缘气体在径向上温度分布存在梯度,会引起内部绝缘气体径向上密度分布不均.在重力及升浮力作用下,绝缘气体发生自然对流,导体上方密度较小的气体流速较高,更多的热量通过对流换热到达外壳上部,由图 3(b)可见,外壳温度在径向出现分层现象,上部温度比下部温度要高一些.在管道轴向,由于在廊道内进行泵风,空气在流过GIL管道的过程中被逐渐加热,GIL管道整体的换热能力在轴向上是逐渐衰退的,空气进口侧换热效果好,出口侧换热效果较差,因此图 3(d)中外壳的温度左至右是逐渐增大的.由图 3(c)中可见,在轴向上,进口侧绝缘气体因换热更为强烈,绝缘气体发生自然对流时,进口侧速度波动整体上高于出口侧,这样导体轴向的温度分布从进口侧到出口侧逐渐升高.由此导体和外壳在内部绝缘气体的自然对流下,具有明显的三维温度场分布特征.总体来看,由于绝缘气体自然对流时在径向上上部区域速度比下部要大,在轴向上进口侧速度比出口侧要大,从而引起了导体和外壳整体温度的分布不均匀.本文计算假定基本工况下外壳温度差异径向上约为1.6 ℃,轴向上约为3.8 ℃.
| 表 5 基本工况下温度场计算结果 Table 5 Calculated result of temperature field at basic simulation conditions |
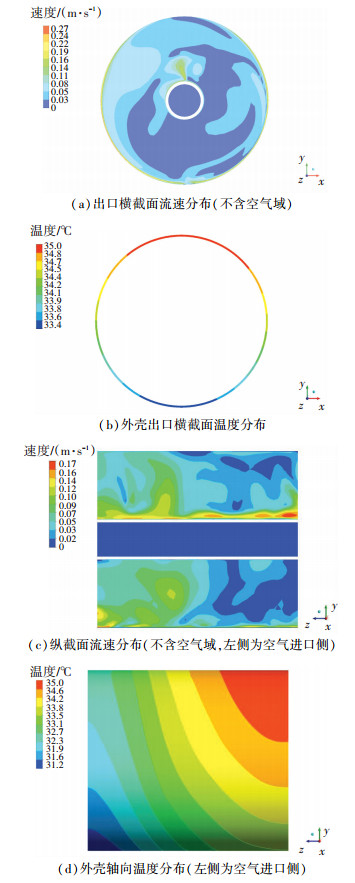
|
图 3 基本工况下的计算结果 Figure 3 Calculated result at basic simulation conditions |
GIL运行过程中,在管廊内通风是有效的散热方式.保持表 3中其他参数不变,只改变GIL外部计算域内空气的进口速度,图 4给出了不同泵风速度下GIL导体与外壳的平均温度计算结果.
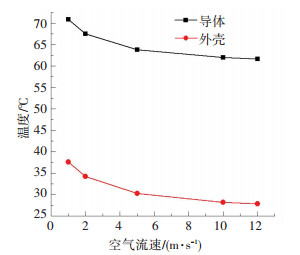
|
图 4 空气流速对GIL温度的影响 Figure 4 Influence of air flow rate on the temperature of GIL |
由图 4可以看出,随着空气流速的增加,GIL管道的整体温度下降,导体与外壳温度变化趋势基本一致,不同风速下两者之间的温差维持一个恒定值,约为33 ℃. GIL温度与空气流速大小呈现非线性特点:当风速较低时,增加空气流速具有较好的散热效果,GIL温度下降很明显;当风速较高,达到10 m/s以上时,GIL温度基本保持水平不变状态,这表明继续增大泵风,对GIL的散热效果作用不佳.
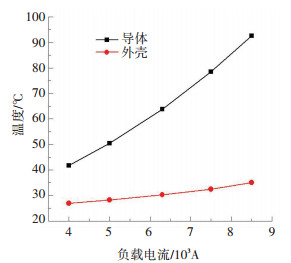
2.2.2 负载电流对GIL温度的影响GIL运行过程中会出现在不同负载电流下的运行状况,保持表 3中其他参数不变,选定工程设计范围内的负载电流,图 5给出不同负载电流条件下GIL的温度变化计算结果.
|
图 5 负载电流对GIL温度的影响 Figure 5 Influence of load current on the temperature of GIL |
由图 5可以看出, 随着负载电流的增加,GIL的温度呈指数式增长.导体温度随负载电流的加大而急速升高,而外壳温度增加的较为缓慢,这样两者之间的温差随着负载电流的加大而越来越大.因此GIL应尽量避免高负荷的过载电流运行情况,否则将会因导体过热原因给GIL安全运行带来隐患,甚至发生严重事故.
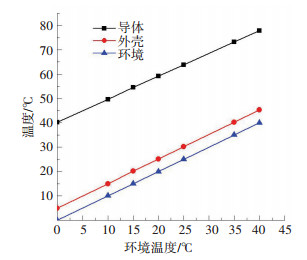
2.2.3 环境温度对GIL温度的影响GIL是全年全天候运行的,所以在不同的季节、时间,运行所处的环境温度都会发生变化,保持表 3中其他参数不变,选定不同的环境温度,图 6给出了不同环境温度下GIL的温度计算结果.
|
图 6 环境温度对GIL温度的影响 Figure 6 Influence of ambient temperature on the temperature of GIL |
由图 6可以看出,GIL的温度随着环境温度的增加而增加,而且呈现出线性变化特点,导体与环境温度之间的温差基本保持不变,约为38 ℃,而外壳与环境之间一般相差5 ℃.因此,在基本运行工况参数下,外界环境温度这单一因素发生变化,很容易评估出GIL的导体和外壳温度.
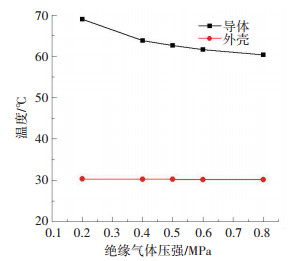
2.2.4 绝缘气体压强对GIL温度的影响GIL管道内充满了一定压力的绝缘气体SF6,由于不可避免在运行过程中存在一定程度的泄露,绝缘气体的压力会逐步降低.同样保持表 3中其他参数不变,选定不同的绝缘气体压强,图 7给出了不同绝缘气体压强下GIL的温度计算结果.
|
图 7 绝缘气体压强对GIL温度的影响 Figure 7 Influence of the pressure of insulation gas on the temperature of GIL |
由图 7可以看出, 随着绝缘气体压强的增加,GIL内部的热量输出能力增强,导体温度先迅速降低,至0.5 MPa时导体温度缓慢降低; 然而, 内部绝缘气体压力的变化并不会带来外壳温度的改变,外壳温度一直会保持不变.这一结论与Minaguchi等[1]的实验结果是一致的,产生此现象的原因可能是增加气体压力,导致气体密度增大,则气体在吸收更多热量的同时可以保持自身温度基本不变,所以导体温度降低而外壳温度基本不变.
同时,由式(1)[18]可知,在低压条件下气体的热传导所传输的热量受压强影响较大,随着压力的升高,压力对气体热传导所传输的热量的影响减小.
| $ \frac{1}{{{Q_0}}} = \frac{1}{Q} + \frac{B}{p}. $ | (1) |
式中:Q0为气体热传导所传输的热量;Q为不考虑压强时的换热量,为定值;B为常数;p为气体压强.
根据以上分析,增加绝缘气体压强可以有助于导体散热,降低导体温度.但是气体压强对导体温度的影响有限,即当压强超过0.5 MPa后,继续增大压强对于导体的散热影响不大,所以从制造、安装、经济角度综合考虑,绝缘气体压强为0.4~0.5 MPa比较合适.同时在GIL运行过程中需对管道内气体压力进行监测,当管道因为漏气等原因导致气体压力降低时,有可能产生过热的情况,需及时发现并解决.
2.2.5 外壳内表面和导体外表面的表面发射率对GIL温度的影响GIL管道的散热方式主要是通过对流和辐射,而辐射换热与管道表面的发射率有关. GIL使用的材料为铝合金,现考虑以下几种表面情况下的表面发射率对GIL管道温度的影响:1)表面抛光,表面发射率0.05;2)镉黄油漆,表面发射率0.20;3)铝表面氧化,表面发射率0.50;4)耐热漆,表面发射率0.90;5)黑色暗淡漆,表面发射率1.00 GIL的辐射换热中考虑辐射的表面为导体外表面、外壳内表面及外壳外表面,本文重点研究了导体外表面及外壳内表面表面发射率对换热的影响,外壳外表面表面发射率取定值0.80.
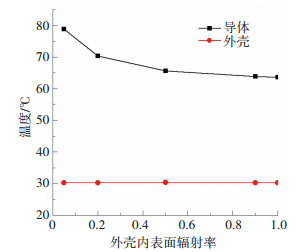
首先,保持导体外表面的表面发射率不变,以基本工况参数为设定的边界条件,改变外壳内表面的表面发射率. 图 8给出了不同外壳内表面发射率下的GIL温度计算结果.
|
图 8 外壳内表面辐射率对GIL温度的影响 Figure 8 Influence of the emissivity of the inner surface of enclosure on the temperature of GIL |
由图 8可以看出,随着外壳内表面发射率的增加,导体温度明显下降,且表面发射率较小时增加发射率对于导体降温有较好的效果,当外壳内表面发射率高于0.6之后,增加发射率对于导体散热的效果将减弱.然而外壳温度不会随外壳内表面的表面发射率改变而发生变化.
这一结论与Minaguchi等[1]的实验结果一致,可能的原因是:由于增大外壳内表面发射率后,导体通过辐射传热的方式散发的热量更多,有利于导体散热;而外壳散热主要通过外壳外表面对周围环境的辐射以及对流传热,这两种方式由于受气体温度、流动及辐射的共同影响,综合而产生的效果是外壳温度基本保持不变.
下面分析导体外表面的表面发射率对GIL温度的影响,此时,外壳内表面发射率取为0.90,同样以基本工况参数为设定的边界条件,改变导体外表面的表面发射率. 图 9给出了不同导体外表面发射率下的GIL温度计算结果.
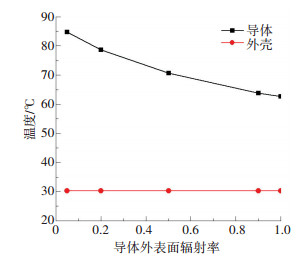
|
图 9 导体外表面辐射率与GIL温度的关系 Figure 9 Influence of the emissivity of the outer surface of conductor on the temperature of GIL |
由图 9可以看出,导体外表面的表面发射率对于导体的散热影响巨大,在发射率由0.05变为1.00时,导体的温度从88.3 ℃下降到65.4 ℃,散热效果非常突出.不过外壳散热主要受外界气流环境影响,因此外壳温度不会受到导体外表面的影响,其数值都将保持不变.综合表面发射率的影响,即使外壳温度不受这些表面发射率的影响,但对于导体的大幅度降温有非常显著的效果,因此在GIL设计时,选择合适的涂料,特别是对于导体的外表面,其次是外壳的内表面,应尽可能的增大其表面发射率,从而降低导体的运行温度.
3 结论1) 引入空气计算域,并采用流固耦合及在流体耦合面施加表面发射率的方法,建立了三维GIL温度场有限元计算模型.基于公开文献的实验数据,验证了计算GIL温度场模拟方法的可靠性.
2) 结合廊管特高压GIL的运行工况特点,采用此模型分析计算了不同空气流速、负载电流、环境温度、绝缘气体压强、表面发射率条件下某国产1 000 kV的GIL热特性.
3) 由于在模型中考虑了空气流速,所以GIL温度场不仅在横截面上的分布是分层的,在轴向方向上温度场的分布也出现了分层现象.
4) 随着空气流速的增大,GIL管道温度降低,导体与外壳温度变化基本一致.当风速较低时, 增加风速可以显著降低GIL温度;当风速较高,达到10 m/s以上时,增加风速对GIL散热效果不佳.
5) 随着负载电流的增加,GIL管道的温度将快速升高,且导体的温升速度远高于外壳的温升速度,导体与外壳温差急速增大.
6) GIL管道的温度与环境温度呈现线性特点,外壳与环境温差基本保持不变,导体与外壳温差随环境温度的升高略有减小.
7) 随着绝缘气体压强的增加,有利于GIL导体的散热,导体温度将降低,外壳温度基本保持不变.但当绝缘气体压强高于0.5 MPa后,继续增大压强对于导体散热效果的影响将减小.
8) GIL外壳内表面及导体外表面的表面发射率对于导体温度影响较大,增大以上两个表面的发射率有助于导体温度的降低,而对于外壳温度几乎无影响.当表面发射率高于0.6之后,导体温度对于导体外表面的发射率的变化更加敏感.
| [1] |
MINAGUCHI D, GINNO M, ITAKA K, et al. Heat transfer characteristics of gas-insulated transmission lines[J]. IEEE Transactions on Power Delivery, 1986, 1(1): 1-9. DOI:10.1109/MPER.1986.5528218 |
| [2] |
COOKSON A H, PEDERSEN B O. Thermal measurements in A 1 200 kV compressed gas insulated transmission line[C]//1979 7th IEEE/PES Transmission and Distribution Conference and Exposition. Atlanta: IEEE, 1979: 163-167.
|
| [3] |
XING Weijun, LI Kang, ZHANG Guoqiang, et al. Experimental study on the cooling performances of gas mixtures with fluorocarbon used in gas insulated transmission line[C]// 2010 International Conference on Electrical Machines and Systems. Incheon: IEEE, 2010: 1469-1472.
|
| [4] |
KOCH H, CHAKIR A. Thermal calculations for buried gas-insulated transmission lines (GIL) and XLPE-cable[C]// 2001 IEEE Power Engineering Society Winter Meeting. Columbus: IEEE, 2001: 857-862.
|
| [5] |
SCHOFFNER G, LÖBL H, ROGLER R D, et al. Thermal calculations of gas insulated transmission lines GIL based on thermal networks[C]// 2004 International Conference on Power System Technology. Singapore: IEEE, 2004: 1029-1036.
|
| [6] |
SONG Xudong, JIN Yilin, ZHU Ximeng, et al. Thermal circuit model of gas-insulated transmission line based on the finite element method[C]// 2017 2nd International Conference on Electrical and Electronics: Techniques and Applications. Beijing: Science and Engineering Research Center, 2017: 70-79.
|
| [7] |
BENATO R, DUGHIERO F. Solution of coupled electromagnetic and thermal problems in gas-insulated transmission lines[J]. IEEE Transactions on Magnetics, 2003, 39(3): 1741-1744. DOI:10.1109/TMAG.2003.810393 |
| [8] |
KIM S W, KIM H H, HAHN S C, et al. Coupled finite-element-analytic technique for prediction of temperature rise in power apparatus[J]. IEEE Transactions on Magnetics, 2002, 38(2): 921-924. DOI:10.1109/20.996237 |
| [9] |
KIM J K, HAHN S C, PARK K Y, et al. Temperature rise prediction of EHV GIS bus bar by coupled magnetothermal finite element method[J]. IEEE Transactions on Magnetics, 2005, 41(5): 1636-1639. DOI:10.1109/TMAG.2005.846117 |
| [10] |
吴晓文, 舒乃秋, 李洪涛, 等. 气体绝缘输电线路温升数值计算及相关因素分析[J]. 电工技术学报, 2013, 28(1): 65-72. WU Xiaowen, SHU Naiqiu, LI Hongtao, et al. Temperature rise numerical calculation and correlative factors analysis of gas-insulated transmission lines[J]. Transactions of China Electrotechnical Society, 2013, 28(1): 65-72. |
| [11] |
NOVÁK B, KOLLER L. Steady-state heating of gas insulated busbars[C]// Transmission and Distribution Conference and Exposition, 2012 IEEE PES. Orlando: IEEE, 2012: 1-7.
|
| [12] |
王健, 陈超, 李庆民, 等. 基于热力耦合分析的GIL热致伸缩特性及其影响因素[J]. 高电压技术, 2017, 43(2): 429-437. WANG Jian, CHEN Chao, LI Qingmin, et al. Thermal-induced flexible property of gas insulated lines and influencing factors based on thermal mechanical coupling analysis[J]. High Voltage Engineering, 2017, 43(2): 429-437. |
| [13] |
陶文铨. 数值传热学[M]. 第2版. 西安: 西安交通大学出版社, 2001: 1-6.
|
| [14] |
ETEIBA M B, MAMDOUH M, AZIZ A, et al. Heat conduction problems in SF6 gas cooled-insulated power transformers solved by the finite-element method[J]. IEEE Trans on Power Delivery, 2008, 23(3): 1457-1463. DOI:10.1109/TPWRD.2008.915793 |
| [15] |
谈和平, 易红亮. 多层介质红外热辐射传输[M]. 北京: 科学出版社, 2012.
|
| [16] |
阮全荣, 谢小平. 气体绝缘金属封闭输电线路工程设计研究与实践[M]. 北京: 中国水利水电出版社, 2011.
|
| [17] |
肖明清, 袁骏, 赵建, 等. 淮南-南京-上海1 000 kV交流特高压苏通GIL管廊工程隧道总体设计[C]// 2016年中国电机工程学会年论文集. 南京: 中国电机工程学会, 2016: 1-6.
|
| [18] |
朱兴国, 吴乃爵, 徐来定. 用热线法测定气体的导热系数[J]. 物理实验, 1985, 5(2): 57-58+54. ZHU Xingguo, WU Naijue, XU Laiding. Measurement of gas thermal conductivity with the method of hot-wire[J]. Physics Experimentation, 1985, 5(2): 57-58+54. |
 2018, Vol. 50
2018, Vol. 50


