2. 西安交通大学 能源与动力工程学院, 西安 710049
2. School of Energy and Power Engineering, Xi'an Jiaotong University, Xi'an 710049, China
近年来,喷雾被广泛应用在食品冷冻、保鲜、工业冷却、干燥、除尘,医疗等方面,而其中以液氮为工质的低温喷雾,由于其降温快、温度低、污染小的特点,在食品速冻、皮肤病治疗,特别是低温环境获得方面中发挥了重要的作用.对于大型飞行器的高雷诺数气动试验,低温风洞是一个最有效的方法.而作为低温风洞中实现均匀温度场最为重要的降温措施,液氮喷雾的设计显得尤为重要.研究氮液滴碰撞是研究低温流体喷雾问题的基础,对揭示喷雾冷却中雾场液滴行为和指导喷雾设计有重要的意义.
关于液滴碰撞的研究早期主要来源于气象学,因此对象大都为水滴,气流速度也较低. Brazier-Smith等[1]在不同的液滴直径比、相对速度及球心距离下进行了一系列水滴碰撞实验,观察到了反弹、永久合并、合并后分离、合并后分离并伴随小液滴形成这4种典型的相互作用. Ashgriz等[2]对水滴碰撞后的两种分离形态——反射分离和拉伸分离进行了实验研究. Brenn等[3]对液滴在拉伸分离时子液滴的生成规律进行了实验研究.液滴碰撞的数值模拟主要分为两类:一类是传统的网格方法,例如流体体积法(VOF)、水平集法(level set)等;另一类是无网格法,例如分子动力学方法(MD)等. Tanguy等[4]采用水平集法追踪气液界面,与前人的实验结果对比,取得了良好的一致性,但发现此方法存在可能引起质量损失的缺陷. Ko等[5]考虑液滴撞击引发的破碎过程,提出了一个新的液滴碰撞模型,可以预测子液滴的数目、大小及速度. Nikolopoulos等[6-8]采用流体体积法(VOF)分别对同尺寸液滴对心碰撞、同尺寸液滴偏心碰撞、以及不同尺寸液滴对心碰撞进行了详细的数值研究. Zeoli等[9]研究了高压气体雾化技术中临界液滴破碎的情况,建立了数值模型,并进行了实验验证,针对1~5 mm的大液滴进行了气流下的对比验证. Floury等[10]研究了油水混合物中高压阀门后液滴的破碎和再合成的情况,结果表明压力起决定作用. Lasheras等[11]使用多普勒粒度仪检测了高速水射流后破碎形成的液滴,用局部各向同性的经典概念来定性地解释了远处的液滴尺寸分布及其大气中水蒸气比例对粒径分布的影响. Christanti等[12]研究了聚合物对于射流雾化的影响因素,结果表明聚合物的分子质量增加会减弱聚合物的破碎. Sazhin等[13]在模拟燃油液滴时研究了液滴内部温度对液滴蒸发破碎的影响.结果表明,液滴内部温度变化会增加燃油表面的温度从而增加破碎概率.张彬等[14]采用流体体积法(VOF),研究了不同碰撞参数对液滴与壁面碰撞力的影响.夏盛勇等[15]对三氧化二铝液滴对心碰撞进行了数值模拟,得到了反弹、变形后聚合及自反分离这3种碰撞结果,并得出了对应的临界韦伯数.魏明锐等[16]在随机碰撞模型的基础上,全面考虑了液滴碰撞反弹、集合、反射分离和摩擦分离的情况,并用于KIVA程序中,改善了由于聚合而导致液滴半径较大的问题.
综上所述,国内外学者对于高速气流下的运动液滴行为研究得较少,同时对于低温工质,特别是氮液滴的研究十分欠缺.研究发现液体黏性和表面张力是影响液滴碰撞破碎特性的重要参数,液氮的黏度比较低,韦伯数比水和油等流体小,因此与水滴之间的碰撞特性不同.
本文基于研究水液滴碰撞破碎的方法,进一步深入分析氮液滴的情况.使用流体体积法(VOF)建立了氮液滴的碰撞模型,对液滴在高速气流下的碰撞过程进行了数值模拟,着重研究了碰撞过程中液滴形态及气隙压力等参数的变化特性.
1 数值计算模型与方法 1.1 控制方程在描述牛顿流体的流动现象时,N-S方程具有最合适的形式.牛顿流体的流动过程是一个包括内摩擦、热量传递及质量扩散等现象的具有耗散性质的过程.当流体为不可压常黏度流体时,N-S方程有如下形式:
| $ \begin{array}{l} \rho \left( {\frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}} \right) = \rho {g_x} - \frac{{\partial p}}{{\partial x}} + \\ \mu \left( {\frac{{{\partial ^2}u}}{{\partial {x^2}}} + \frac{{{\partial ^2}u}}{{\partial {y^2}}} + \frac{{{\partial ^2}u}}{{\partial {z^2}}}} \right), \\ \rho \left( {\frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}}} \right) = \rho {g_y} - \frac{{\partial p}}{{\partial y}} + \\ \mu \left( {\frac{{{\partial ^2}v}}{{\partial {x^2}}} + \frac{{{\partial ^2}v}}{{\partial {y^2}}} + \frac{{{\partial ^2}v}}{{\partial {z^2}}}} \right). \end{array} $ |
不可压缩流体连续方程为
| $ \frac{{\partial u}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = 0. $ | (1) |
由于N-S方程有4个未知数,因此需要与式(1)联立求解.近年来,随着CFD技术的飞速发展,商业软件的大量应用,在N-S方程的求解方面已取得较大突破.
1.2 VOF方法VOF方法是欧拉-欧拉法的一种,它是一种应用在固定欧拉网格上的表面追踪技术.在每个控制单元内,所有相的体积分数和为1.单元内的物性等变量值由各相共享,并且代表了体积平均值.
对相界面的追踪是通过求解相连续性方程从而得到该相的体积分数来实现的.对于不作为主相的第i相,方程具有如下形式:
| $ \frac{{\partial {\alpha _i}}}{{\partial x}} + {\mathit{\boldsymbol{v}}_i} \cdot \nabla {\alpha _i} = \frac{{{S_{{\alpha _i}}}}}{{{\rho _i}}}. $ |
式中:αi为单元内第i相流体的体积分数,vi为单元内第i相流体的速度,ρi为单元内第i相流体的密度,Sai为质量源项.
对于主相,体积分数则通过下式求解:
| $ \sum\limits_{i = 1}^n {{\alpha _i} = 1.} $ |
对整个计算域求解单一的动量方程,得到的速度场由各相共享,方程如下:
| $\begin{array}{l} \frac{\partial }{{\partial t}}\left( {\rho \mathit{\boldsymbol{v}}} \right) + \nabla \cdot \left( {\rho \mathit{\boldsymbol{vv}}} \right) =- \nabla \rho + \nabla \cdot \left[{\mu \left( \nabla \right.\mathit{\boldsymbol{v}} + } \right.\\ \left. {\left. {\nabla {\mathit{\boldsymbol{v}}^{\rm{T}}}} \right)} \right] + \rho g + \mathit{\boldsymbol{F}}. \end{array} $ |
式中:ρ为流体密度,μ为动力黏度.
同样,能量方程也是由各相共享,方程如下:
| $ \frac{\partial }{{\partial t}}\left( {\rho E} \right) + \nabla \cdot\left[{\mathit{\boldsymbol{v}}\left( {\rho E + p} \right)} \right] = \nabla \left( {{k_{{\rm{eff}}}}\nabla T} \right) + {S_{\rm{h}}}. $ |
式中:keff为有效热导率;Sh为源项,包括辐射以及其他体积热源;E为总能量.
本文通过上述理论,选取20 mm×20 mm的正方形区域作为计算区域,划分200×200的四边形结构化网格,采用VOF方法追踪界面变形,通过求解两相容积比率的连续性方程来跟踪相界面.使用ANSYS Fluent建立三维非稳态模型,并进行求解.
1.3 碰撞重要参数首先给定液滴碰撞中几个重要参数的定义.碰撞参数B定义为
| $ B = 2X/\left( {{D_{\rm{s}}} + {D_{\rm{b}}}} \right). $ |
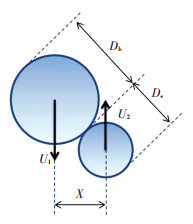
式中:B表示的液滴碰撞的取值范围为0 ≤ B<1,B = 0表示液滴对心碰撞,0<B<1表示液滴偏心碰撞; X为垂直碰撞方向的液滴中心间距;Ds为两液滴中较小液滴的直径;Db为较大液滴的直径. 图 1为液滴碰撞示意图.
|
图 1 液滴碰撞示意 Figure 1 Droplet collision schematic |
液滴直径比Δ定义为
| $ \mathit{\boldsymbol{ \boldsymbol{\varDelta} = }}{D_{\rm{s}}}/{D_{\rm{b}}}. $ |
式中,Δ=1表示两个相同尺寸液滴的碰撞,Δ<1表示不同尺寸液滴的碰撞. Δ越小,则液滴尺寸差异越大.
韦伯数We定义为
| $ We = \rho {v^2}l/\sigma . $ |
式中:ρ为气体密度,v为液滴相对气体的速度,l为特征长度,σ为表面张力系数.
2 计算结果 2.1 模型可靠性验证Ashgriz等[2]在1990年进行了水滴碰撞实验,在不同的碰撞初始条件下得到了反射分离及拉伸分离的结果.本文从文献[2]中选取了3个工况,并设置一个20 mm×20 mm的区域来进行液滴碰撞的模拟研究.在一个100 mm×100 mm的区域研究气隙压力的变化及影响.将本文的数值模拟结果与文献[2]实验结果进行了对比,如图 2所示.可以看出模拟结果与实验符合较好,模拟得到的液滴形态与实验中拍摄的液滴形态基本一致.因此,可以认为本文的计算模型适用于液滴碰撞过程的模拟.
2.2 高速气流下相同尺寸液滴对心碰撞在有一定气流速度的背景环境下,对两个相同尺寸的液滴对心碰撞过程进行了模拟,计算参数如下:气流温度选择低温风洞最低运行工况T=110 K,气流速度ua=10 m·s-1,液滴直径Ds=Db=0.8 mm,液滴直径比Δ=1,液滴速度u1=u2=7 m·s-1,相对速度ur=14 m·s-1,碰撞参数B=0,韦伯数We=41.6.直径的选取是根据实际液氮喷雾实验,本文实验测定液滴粒径分布最大液滴直径在0.8 mm.液滴形态的时序图如图 3所示.从图 3中可以看出,在两液滴尚未接触的开始时刻,由于气流的影响,液滴已经产生了较大变形;随后于0.30~0.35 ms时间段内,两液滴前端开始接触并逐渐挤压,液滴间隙内气体被压缩;但由于液滴初始动能大于压力能,在0.40~1.20 ms时间段内气体进一步被压缩,液滴逐渐挤压形成扁平状,并向两边扩展,向液滴后部伸展的部分由于受到气流的影响,在达到一定长度后被气流阻碍,并破碎产生数个子液滴,与伸展的主体部分开始沿气流方向运动,同时液滴前端继续向前伸展,整个液滴被拉伸形成细长的带状;1.2 ms之后,由于液滴运动能量超过了表面能,带状液滴断裂,形成许多子液滴,并继续沿气流方向运动.

|
图 3 高速气流下相同尺寸液滴对心碰撞时序图 Figure 3 The same diameter droplets central collision timing diagram under high-speed airflow |
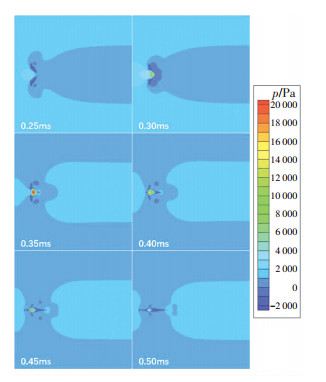
本文还对液滴碰撞中内部产生的气隙压力进行了分析.在液滴碰撞时,会在液滴内部产生气隙,这小部分的气体会对后续的液滴破碎形态造成影响.工程中比较重视液滴碰撞破碎之后的粒径,间隙压力释放的快慢和最高压力对于液滴的破碎粒径大小会造成一定的影响. 图 4为同尺寸液滴对心碰撞过程在碰撞时刻(0.25 ~ 0.5 ms)气体间隙内压力的变化过程.
|
图 4 相同尺寸液滴对心碰撞过程中气隙压力变化 Figure 4 The pressure variation of same diameter droplets central collision under high-speed airflow |
由图 4可以看出,在液滴开始运动到开始接触时,气隙内压力呈现逐渐升高趋势,在0.35 ms时刻左右,即液滴部分接触但并未完全合并时,气隙内压力达到最大值;随后,由于液滴初始动能大于压力能,气隙内气体被完全挤出,压力也逐渐回落,直至液滴完全合并.
2.3 高速气流下不同尺寸液滴对心碰撞在以上计算的基础上,改变其中一个液滴的尺寸,对高速气流下不同尺寸液滴的对心碰撞过程进行了模拟.计算参数为:气流温度T=110 K,气流速度ua= 10 m·s-1,液滴直径Ds= 0.4 mm,Db= 0.8 mm,液滴直径比Δ= 0.5,液滴速度u1=u2=7 m·s-1,相对速度ur=14 m·s-1,碰撞参数B=0,大液滴韦伯数We=41.6,小液滴韦伯数We=20.8.液滴形态的时序图如图 5所示.

|
图 5 高速气流下不同尺寸液滴对心碰撞时序图 Figure 5 Two different diameter droplets central collision timing diagram under high-speed airflow |
对比图 5与图 3可以看出,液滴尺寸比对液滴破碎结果有显著影响.由于较大液滴动量较大,因此合并后的液滴会继续沿着较大液滴的速度方向运动,加上气流的影响,液滴拉伸并下凹,呈现近似弓形的形状;随后在气流的作用下,弓形液滴从两端开始分离出子液滴,并逐渐延伸到中部,最终完全破碎,两端分离的子液滴较小,中部的子液滴较大.
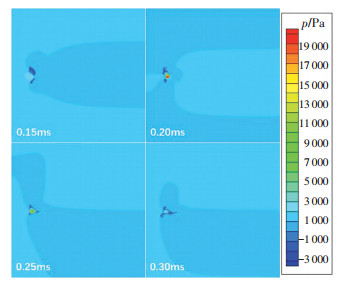
图 6为不同尺寸液滴对心碰撞过程中液滴碰撞时刻(0.15 ~ 0.30 ms)气体间隙内压力的变化过程.与图 4类似,气隙内压力呈现出先增大后减小的趋势. 图 4中压力释放为来流的下游方向,图 6中压力释放为来流的斜下游方向.这是由于直径比不为1,因此气隙内压力释放向着液滴方向小的下方释放,呈现不对称情况,在来流速度的带动下,随着气流向下游发展,气隙压力便朝向斜下方.上部液滴粒径大,影响了后续的压力分布,在0.3 ms时表现为上半部分压力大.
|
图 6 不同尺寸液滴对心碰撞过程中气隙压力变化 Figure 6 The pressure variation of two different diameter droplets central collision under high-speed airflow |
计算参数为:气流温度T=110 K,气流速度ua= 10 m·s-1,液滴直径Ds=Db=0.8 mm,液滴直径比Δ=1,液滴速度u1=u2=7 m·s-1,相对速度ur= 14 m·s-1,碰撞参数B=0.5,韦伯数We=41.6. 图 7为液滴形态的时序图,将图 7与图 3进行对比,首先可以看出,对于碰撞参数不为0,即液滴偏心碰撞的情况,碰撞后液滴拉伸的方向有明显不同.对心碰撞时,液滴拉伸方向趋近于水平方向,在液滴尺寸相同时则为完全水平;而偏心碰撞时液滴的扩展方向与水平方向的动量在碰撞过程中相互抵消,残余的动能会沿水平方向释放;而偏心碰撞时,液滴水平和竖直方向的动量都不能完全抵消,残余的动量经过合成,最终沿倾斜方向释放.从图 7中还可以看出,液滴的破碎形态与上一个工况类似,都是从两端逐渐扩散到中间部分,最终碎裂成数个子液滴.

|
图 7 高速气流下相同尺寸液滴偏心碰撞时序图 Figure 7 The same diameter dropletseccentric collision timing diagram under high-speed airflow |
图 8为同尺寸液滴偏心碰撞时液滴内气隙压力的变化过程.对比图 8与图 4可以看到,偏心碰撞气隙压力的形态和破碎形态相似,在上方呈现韧性带状.下方由于来流的影响,韧性带的不完整导致压力聚集在碰撞处附近.相较对心碰撞过程,偏心碰撞时的气隙压力会更快释放,这是由于偏心碰撞过程伴随着液滴的旋转,使间隙内气体更快的被挤出.

|
图 8 相同尺寸液滴偏心碰撞过程中气隙压力变化 Figure 8 The pressure variation of same diameter dropletseccentric collisionunder high-speed airflow |
实际工况中,不同尺寸的液滴偏心碰撞是最常见的,对这种情况进行了模拟研究.计算参数为:气流温度T=110 K,气流速度ua= 10 m·s-1,液滴直径Ds= 0.4 mm,Db=0.8 mm,液滴直径比Δ=0.5,液滴速度u1=u2=7 m·s-1,相对速度ur=14 m·s-1,碰撞参数B=0.5,大液滴韦伯数We=41.6,图 9为液滴形态的时序图.对比图 9与图 5可以发现,除去形状朝向的差别,两种工况下的液滴破碎形态十分类似,这说明当液滴尺寸差异较大时,碰撞参数对碰撞结果的影响不大,碰撞结果主要由液滴直径比等参数所决定.

|
图 9 高速气流下不同尺寸液滴偏心碰撞时序图 Figure 9 Two different diameter droplets eccentric collision timing diagram under high-speed airflow |
本文建立了液滴碰撞模型,采用VOF方法对氮液滴在高速气流中的碰撞过程进行了数值模拟,得到了碰撞过程中不同时刻液滴的形态.通过改变计算初始条件,研究了碰撞参数B、液滴尺寸比Δ等参数对碰撞过程的影响,结论如下:
1) 韦伯数较大时,液滴拉伸形成很长的韧性带,随后在自身运动及气流的作用下剧烈破碎.随着液滴破碎,特征尺寸的减小,韦伯数也会随之减小,液滴不再发生破碎.破碎后的液滴在气流速度的影响下,向下游运动.
2) 高速气流下液滴发生碰撞时,碰撞参数B主要决定液滴拉伸形成韧性带的方向.当B为0时,液滴对心碰撞,韧性带呈水平方向.当0<B<1时,液滴偏心碰撞,液滴水平和竖直方向的动量都不能完全抵消,残余的动量经过合成,最终沿倾斜方向释放,形成倾斜的韧性带.
3) 对比模拟中两种不同液滴尺寸比Δ结果发现,在Δ=1相同直径液滴的情况下,相同时间内,表面张力作用的连续韧性带长度相较Δ=0.5不同直径液滴碰撞的情况要长,Δ=0.5工况下液滴更迅速地破碎为液滴.
4) 液滴接触时形成的气体间隙,其压力呈现先增大后减小的趋势;相较对心碰撞过程,由于偏心碰撞时伴随着液滴的旋转,其气隙压力会更快释放.
通过研究氮液滴碰撞之后的形态变化和液滴粒径的相图,分析观察碰撞过程后存在的较大液滴,并确认其方位,从而设计出合适的喷嘴和喷雾方向.气隙压力的变化反映了液滴碰撞分离的过程,影响韧性带方向,从而影响大液滴的分布.因此在设计和应用安装时要尽量考虑液滴分离形态情况,尽量做到完全蒸发.
| [1] |
BRAZIER-SMITH P R, JENNINGS S G, LATHAM J. The interaction of falling water drops: coalescence[J]//Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 1972, 326(1566): 393-408. DOI: 10.1098/rspa.1972.0016.
|
| [2] |
ASHGRIZ N, POO J. Coalescence and separation in binary collisions of liquid drops[J]. Journal of Fluid Mechanics, 1990, 221(1): 183-204. DOI:10.1017/S0022112090003536 |
| [3] |
BRENN G, KOLOBARIC V. Satellite droplet formation by unstable binary drop collisions[J]. Physics of Fluids, 2006, 18(8): 1-18. DOI:10.1063/1.2225363 |
| [4] |
TANGUY S, BERLEMONT A. Application of a level set method for simulation of droplet collisions[J]. International Journal of Multiphase Flow, 2005, 31(9): 1015-1035. DOI:10.1016/j.ijmultiphaseflow.2005.05.010 |
| [5] |
KO G H, RYOU H S. Modeling of droplet collision-induced breakup process[J]. International Journal of Multiphase Flow, 2005, 31(6): 723-738. DOI:10.1016/j.Ijmulti-phaseflow.2005.02.004 |
| [6] |
NIKOLOPOULOS N, NIKAS K S, BERGELES G. A numerical investigation of central binary collision of droplets[J]. Computers & Fluids, 2009, 38(6): 1191-1202. DOI:10.1016/-j.compfluid.2008.11.007 |
| [7] |
NIKOLOPOULOS N, THEODORAKAKOS A, BERGELES G. Off-centre binary collision of droplets: A numerical investigation[J]. International Journal of Heat and Mass Transfer, 2009, 52(19/20): 4160-4174. DOI:10.1016/j.ij-heatmasstransfer.2009.04.011 |
| [8] |
NIKOLOPOULOS N, STROTOS G, NIKAS K S, et al. The effect of Weber number on the central binary collision outcome between unequal-sized droplets[J]. International Journal of Heat and Mass Transfer, 2012, 55(7/8): 2137-2150. DOI:10.-1016/j.ijheatmasstransfer.2011.12.017 |
| [9] |
ZEOLI N, GU S. Numerical modelling of droplet break-up for gas atomisation[J]. Computational Materials Science, 2006, 38(2): 282-292. DOI:10.1016/j.commatsci.2006.02.012 |
| [10] |
FLOURY J, LEGRAND J, DESRUMAUX A. Analysis of a new type of high pressure homogeniser. Part B. study of droplet break-up and recoalescence phenomena[J]. Chemical Engineering Science, 2004, 59(6): 1285-1294. DOI:10.1016/-j.ces.2003.11.025 |
| [11] |
LASHERAS J C, VILLERMAUX E, HOPFINGER E J. Break-up and atomization of a round water jet by a high-speed annular air jet[J]. Journal of Fluid Mechanics, 1998, 357: 351-379. DOI:10.1017/S0022112097008070 |
| [12] |
CHRISTANTI Y, WALKER L M. Surface tension driven jet break up of strain-hardening polymer solutions[J]. Journal of Non-Newtonian Fluid Mechanics, 2001, 100(1): 9-26. DOI:10.1016/S0377-0257(01)00135-5 |
| [13] |
SAZHIN S S, ABDELGHAFFAR W A, SAZHINA E M, et al. Models for droplet transient heating: effects on droplet evaporation, ignition, and break-up[J]. International Journal of Thermal Sciences, 2005, 44(7): 610-622. DOI:10.1016/j.ijthermalsci.2005.02.004 |
| [14] |
张彬, 韩强, 袁小芳, 等. 液滴与水平壁面碰撞力的数值研究[J]. 西安交通大学学报, 2013, 47(9): 23-27. ZHANG Bin, HAN Qiang, YUAN Xiaofang, et al. Simulation of impact force of drop impacting on horizontal plate[J]. Journal of Xi'an Jiaotong University, 2013, 47(9): 23-27. DOI:10.7652/xjtuxb201309004 |
| [15] |
夏盛勇, 胡春波. 三氧化二铝液滴对心碰撞直接数值模拟[J]. 应用数学和力学, 2014, 35(4): 377-388. XIA Shengyong, HU Chunbo. Direct numerical simulation of head-on binary collision of aluminum oxide droplets[J]. Applied Mathematics and Mechanics, 2014, 35(4): 377-388. DOI:10.3879/j.issn.1000-0887.2014.04.004 |
| [16] |
魏明锐, 文华, 刘永长, 等. 喷雾过程液滴碰撞模型研究[J]. 内燃机学报, 2005, 23(6): 518-523. WEI Mingrui, WEN Hua, LIU Yongchang. Modeling study on droplets collision in spray process[J]. Transactions of CSICE, 2005, 23(6): 518-523. |
 2018, Vol. 50
2018, Vol. 50



