2. 北京山维科技股份有限公司,北京 100043
2. Beijing Sunway Technology Co., Ltd., Beijing 100043, China
供水管网可靠性是指供水管网在一定时间内一定运行条件下完成预定功能的性质[1].管网可靠性分析是供水系统重点研究的问题[2],对管网的设计和运维具有重要指导意义.主流方法大多是在Wagner等(1988)提出的解析法和模拟法的基础上不断深化或者将二者相结合而发展起来的[3-4].解析法主要从管网结构分析发生故障时管网的连通性及从水源点到取水点的可达性;模拟法侧重通过水力模型计算评价供水需求的满足程度.在解析法可靠性分析方面,Quimpo和Shamsi[5]提出了结点对可靠性(NPR)模型,其中,NPR是指某个结点与水源保持连通的可能性;Kansal等[6]基于附加生成树的概念,将管网的整体连通性定义为源结点与所有需求结点同时连通的可能性;Walski[7]将管道故障时关阀停水形成的封闭区域定义为单元(segment),提出单元-阀门(segment-valve,SV)图模型,运用图论方法分析阀门的数量和布局是否满足管网可靠性需求;Jun等[8]则进一步基于SV图提出一系列指标来衡量管网的可靠性.
结构分析之所以成为管网可靠性的重要手段,是因为结构显著影响功能[9],供水需求的满足,依赖于管网结构中从水源到用户的传输路径[10].复杂网络理论为管网结构分析提供了新的思路和方法.Yazdani和Jeffrey[11]应用复杂网络测度指标研究供水管网结构特征,进而探究保障可靠性的管网扩建策略;Hawick[12]用图分析理论通过模拟故障分析供水管网可靠性,研究提高可靠性的措施.
既往研究一般使用节点-连边模型分析供水管网的复杂网络特性[13].但是,节点-连边模型存在一定局限:管段由相邻接的管点所界定,相对较短,空间分布呈现明显的局部化特点;节点连通度绝大多数在1~4,拓扑连接呈现均质性和规则化特征.上述局限使得复杂网络研究的很多理论成果和分析方法,不便运用于供水管网.本文把具有相同口径和材质的顺序相连管段看作同一实体,即“管线”,提出管线对偶图(pipeline dual graph,PDG)模型,在此模型基础上运用复杂网络的理论和方法,对中国3个城市的实际供水管网进行结构测度和鲁棒性分析.由此得到一种适用于PDG模型的供水管网可靠性评价方法和相应的评价指标,可用于设计和运维方案的制定.
1 管线对偶图模型节点-连边模型将三通、四通、阀门、水表等管件统称为管点,相连管点间的管道称为管段,将管点和管段分别抽象为节点和连边,从而形成一个图(graph).但在供水管网规划设计和工程实施中,一般在同一条道路上敷设口径和材质统一的一条完整管道,在接水、维修的施工情境下才会将管道作开管或截断处理.这样的一条管道在供水服务质量方面也具有高度统一性.基于这种观察,本文提出一种新的管网拓扑模型,将顺序相连、无大角度转折的同口径同材质管段序列——管线(pipeline),看作一个统一实体,并抽象为节点,如果两条管线相交,则两管线对应节点用边相连.由此形成的无向图即为管线对偶图(PDG)模型.
1.1 管线生成的连接规则本文中的管线,意指管段按照一定连接规则顺序相连而形成的最大线性实体.由管段相接形成管线的连接规则可描述如下:设管段A的一个端点是w,则与w关联的另一管段B与管段A属于同一管线的充分必要条件是:1)口径和材质与管段A相同(属性一致性规则);2)与管段A在w处的夹角不小于135°,且在所有与w关联的相同口径和材质的管段中与管段A的夹角最大(夹角最大化规则).夹角最大化规则的提出,是基于设计和铺设中管道的实际排布规律.假设图 1中所有管段均具有相同口径和材质,对于图 1(a)中的拐点,因为夹角α≥135°,两管段被认为属于同一管线;对于图 1(b)中的三通,考虑与管段A连接的管段B,因为二者的夹角α≥135°,且该夹角比管段C与管段A的夹角大,所以,管段A与管段B属于同一管线;对于图 1(c)中的四通,因为α、β≥135°,则管段A与C属于同一管线,管段B与D属于同一管线.

|
图 1 管段连接类型 Figure 1 Pipe connection forms |
PDG生成的第一步是依据连接规则对管段集合求解最小划分(使得到的管线数量最小),接着将集合划分中的每个子集(即一条管线)抽象为一个图的节点,最后检查管线间的相交关系.如果两管线相交,则将对应的节点用边相连,从而完成PDG模型.
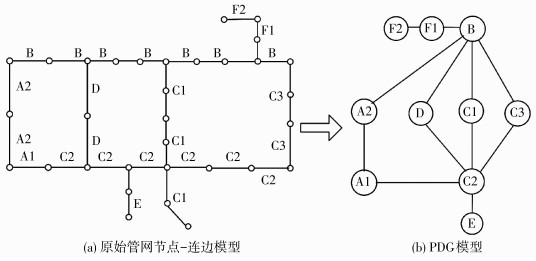
图 2(a)为原始管网的节点-连边模型,对应的PDG如图 2(b)所示.可以看出,PDG模型同时凸显了管道及其连通关系,有利于分析管网结构及其对管网功能的影响.
|
图 2 节点-连边模型及其对应的管线对偶图模型 Figure 2 Node-edge model and the corresponding pipeline dual graph model |
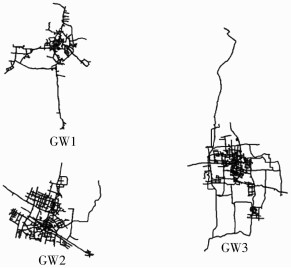
选用广西省某城市和江苏省两个城市口径DN200以上实际供水主干管网作为研究对象,分别记为GW1、GW2和GW3.3个城市的管网总体分布如图 3所示.由于城市形态不同,3个供水管网的空间形态也存在明显差异:GW3管网空间分布范围明显大于前两者,但郊区管网分布稀疏;GW1与GW2的空间范围相近,GW2所在城市地形平坦,管网分布均匀,整体呈网格状分布,而GW1所在的城市多山地和丘陵,城市分布受地形限制,管网分布也不均匀.
|
图 3 供水管网分布 Figure 3 Distribution maps of the water supply networks |
图 4为3个供水管网对应PDG的可视化表达,其中每个节点的坐标设定为原始管网中对应管线全部坐标点的平均值.管网PDG与原始管网的范围和布局大致相同,但是放大局部区域(图 5)可以看出,PDG与原始管网的结构和形态差异较大,PDG中的节点度(连边数量)有明显多样性.

|
图 4 管网PDG模型 Figure 4 PDG models of the 3 water supply networks |

|
图 5 GW3局部放大 Figure 5 Partial enlargement of GW3 |
各管网相应PDG模型的总体特征如表 1所示.其中n表示管点数,m表示管段数,N代表管线数(即PDG中的节点数),M代表管线交叉数(即PDG中的边数),m/N代表管段管线转化比.由表 1可以看出,GW1和GW2的总体规模相近,GW3的规模则是二者的近2倍;GW1管段管线转化比明显大于GW2和GW3,GW2略大于GW3,说明GW1管线规模(包含管段数)较大.
| 表 1 3个管网的特征 Table 1 Characteristics of the 3 networks |
供水管网结构测度指标可分为基本拓扑特征、网络冗余度和网络连通性3类,如表 2所示.其中,平均度 <k>与度分布、平均路径长度L都是体现供水管网拓扑结构总体特征的统计指标.聚类系数C[14]和网格系数Rm[15]主要体现网络的冗余度.谱隙(spectral gap)Δλ定义为网络连接矩阵的最大与次大特征值之差[16-17],代数连通度(algebraic connectivity)λ2定义为图的标准化拉普拉斯矩阵的第二小特征值[18-19],二者均是衡量网络连通性强度的指标.
| 表 2 供水管网结构测度指标 Table 2 Structure metrics of water supply networks |
通过R软件平台环境,运用igraph、Matrix等开源程序包对3个PDG实例进行结构测度,结果如表 3所示.总体看GW2的测度指标全面优于GW1和GW3,特别是谱隙指标Δλ,领先2个数量级以上,表明GW2具有更好的可靠性.GW1和GW3的指标普遍接近,除Δλ之外的其他指标都在一个数量级以内,不足以体现冗余度和连通性的差异[12-13].GW1的谱隙指标Δλ相比GW3有一个数量级的优势,表明GW1的割点、割边等传输瓶颈较少,这类关键部件失效或遭受攻击造成大面积停水的风险较小.
| 表 3 基于PDG模型的结构测度结果 Table 3 Structure metrics based on PDG model |
进一步的可靠性比较,可以在分析度分布的基础上,考察管网对抗攻击(即移除部件)保持结构稳定的鲁棒性.首先考察3个PDG模型的节点度分布是否具有无标度(scale-free)特性.所谓无标度特性,意指节点度为k的可能性p(k)随k的增大而减小,满足p(k) ~ k-r,其中r为幂律分布指数.如果节点度满足幂律分布,复杂网络研究中称之为无标度网络[20],常用模拟攻击方法来考察其结构鲁棒性.这类网络在随机攻击下有较强的鲁棒性,而在高连接度节点遭到攻击时,网络会被分解成独立部分甚至崩溃[21].PDG模型下的度分布图和累计度分布图如图 6(a)、(b)所示,其中纵坐标表示度对应概率.可以看出,3个管网的累计度均呈现明显长尾分布,符合无标度特征.

|
图 6 基于PDG模型的管网度分布与累计度分布 Figure 6 Degree distribution and cumulative degree distribution based on PDG model |
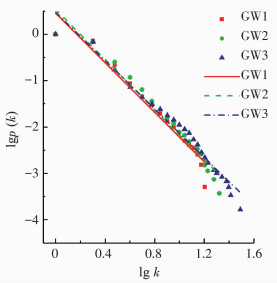
分别对累计度分布概率p(k)及k-r取对数,绘制双对数累计度分布图,如图 7所示.可以看出,3个实例管网的双对数累计度分布图均呈近似线性关系.通过回归分析,求出3个PDG的lg k系数和判定系数R2:GW1为-2.669和0.948;GW2为-2.706和0.956;GW3为-2.611和0.968.两系数存在明显的线性相关关系,进一步验证了供水管网在PDG模型下是无标度网络,从而可以应用复杂网络理论常用的模拟攻击分析方法,研究管网部件被移除(发生随机故障或遭到蓄意破坏)时供水管网的拓扑完整性和连通度[22].
|
图 7 双对数累计度分布 Figure 7 Double logarithmic cumulative degree distribution |
供水管网的结构鲁棒性指管网整体结构对外部干扰和故障的容忍度[20],是可靠性的重要表现,可以模拟管网受到攻击后结构指标的变化来分析.本文选用平均路径长度L,聚类系数C,网络簇数CL和最大连通子图的相对大小S来测度管网结构的变化.L和C分别反映网络全局传输效率和局部传输效率.当网络受到攻击后,逐渐分裂成若干个连通子图,称为网络簇.网络簇数CL可以用于衡量网络结构破坏的程度. S是指最大连通子图节点数与全局网络节点数的比值,能够反映管网受到攻击时保持服务功能的完整度.
模拟攻击的方式是每次选择一个节点,删除该节点及其相连的边,同时删除生成的孤立点,记录去点率f(去除节点的个数占总节点数的比率),计算管网结构测度指标L、C、CL、S;反复执行直至网络中所有节点都被删除为止.对于随机攻击,删除节点的选择是随机的;对于蓄意攻击,一般是根据具体的攻击策略对节点重要性进行降序排列,按照从最重要到次重要的次序来删除节点,观察结构受到的影响.考虑到供水管网PDG的无标度特性,采用复杂网络研究中结果较为显著的两种策略进行蓄意攻击模拟:基于节点度和基于节点介数中心性(betweenness centrality)[24].节点度是与该节点邻接的节点个数,在PDG模型中代表与一条管线连通的其他管线数量;节点介数中心性是经过该节点的最短路径数量占所有节点间最短路径总数的比例[25].
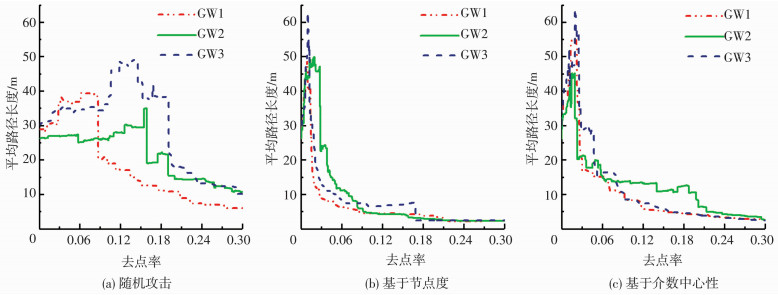
3.2 结果分析分别采用随机攻击、基于节点度攻击和基于节点介数中心性攻击3种策略对3个供水管网进行模拟攻击,各测度指标结果如图 8~11所示.每幅图从左到右分别代表随机攻击、基于节点度攻击和基于节点介数中心性3种策略,3种不同线型的曲线代表3个管网,横坐标代表去点率,纵坐标代表结构测度指标的值.
|
图 8 不同攻击策略下L变化 Figure 8 Changes of L under different attack strategies |
|
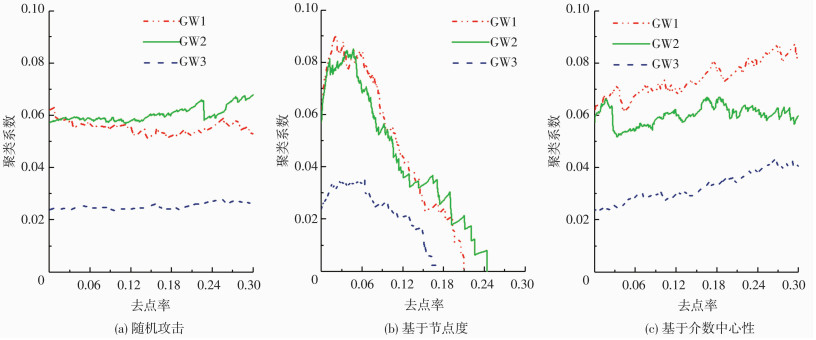
图 9 不同攻击策略下C变化 Figure 9 Changes of C under different attack strategies |
|
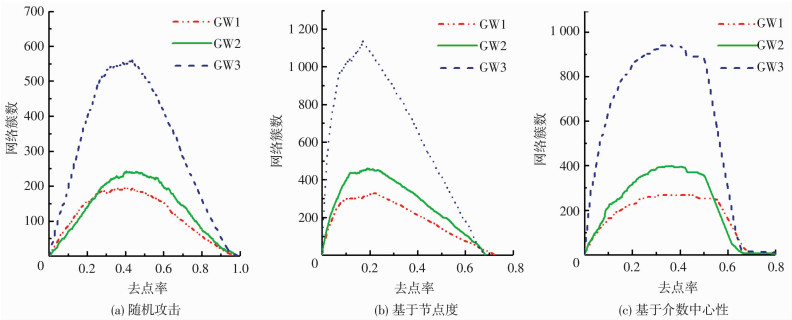
图 10 不同攻击策略下CL变化 Figure 10 Changes of CL under different attack strategies |
|
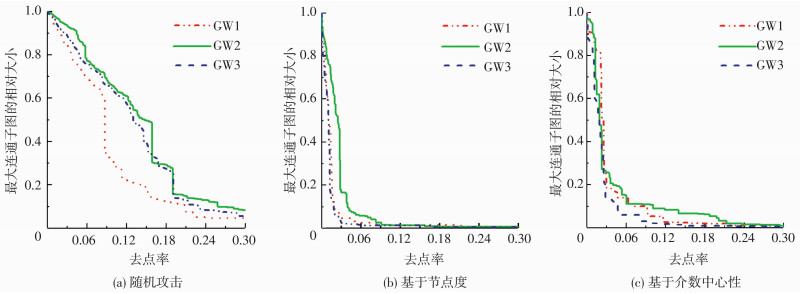
图 11 不同攻击策略下S变化 Figure 11 Changes of S under different attack strategies |
在不同攻击策略下,随着删除节点的增多(去点率f增大),管网结构变化均可分为3个阶段:1)初始期:L急剧增加,网络的传输效率受到明显影响.同时S逐渐下降,CL逐渐上升,说明攻击不断产生规模较小的碎片,但网络尚未分裂,总体运行仍能保持相对平稳.2)分裂期:L到达峰值,然后开始大幅下降,同时S直线下降,CL继续上升.说明网络结构变化剧烈,开始分裂为多个规模相近且相互独立的子图,管网基本瘫痪. 3)崩溃期:L和S由剧烈下降转变为缓慢下降,并逐渐下降至0.此期间CL继续上升并达到最大值,而后由最高点开始下降直至为0.此时网络已失效.
不同攻击模式下管网的结构变化有明显差异.由图 9看出,基于介数中心性攻击和随机攻击两种模式下,聚类系数C变化相对平稳;而在基于节点度的攻击模式下,管网结构变化则相对剧烈.
同一管网在不同攻击策略下,网络结构的变化各不相同.在节点被不断删去时,体现管网结构特征的平均路径长度L、聚类系数C、网络簇数CL和最大连通子图相对大小S 4个指标的变化趋势存在明显差异,相应地进入分裂期和崩溃期的先后大不相同.表 4列出了管网结构发生阶段性变化时的去点率.f1表示由初始期进入分裂期时的去点率,f2表示由分裂期进入崩溃期的去点率.可以看到,基于节点度攻击策略下f1和f2最小,其次是基于介数中心性攻击策略,随机攻击策略下f1和f2最大.这说明基于节点度的攻击是对管网影响最严重的策略,最易造成管网分裂和崩溃,因而连接度大的管线是应该重点保护的对象.
| 表 4 管网不同攻击策略下不同阶段的去点率 Table 4 Removal rate of different attack strategies in different phase |
不同管网在相同攻击策略下,f1、f2也各不相同,f1的差异尤为明显.由表 4可以看出:在节点度和随机攻击策略下,f1的大小顺序均为GW2>GW3>GW1,GW2的鲁棒性最好,其次是GW3,GW1的鲁棒性最差.在介数中心性攻击策略下,GW1的f1和f2略大于后两者,与GW1谱隙测度较高的情况相对应,说明这种攻击策略对管网传输瓶颈比较敏感.
通过结构测度和鲁棒性分析的结果,可以反观3个实际管网的特点.GW1分布很不均匀,管线规模大,管线替代通路少,连通性对管线依赖度高,连接度高的管线对连通的影响很大,但割点割边等传输瓶颈较少;GW2分布均匀规整,环路多,冗余度和健壮性好;GW3管线规模适中,替代通路较充分,但割点割边相对较多,成为管网中的脆弱部分.认识上述特点有助于对管网进行有针对性的保护和优化.
3.3 基于SV图的可靠性评价作为对比,对上述3个实际管网使用Jun等[8]提出的基于SV图的3个基本指标进行可靠性评价:单元平均管道长度La;单元内平均管线数Na;长度阀门比L/V.结果如表 5所示.
| 表 5 3个管网的SV模型分析结果 Table 5 Results of SV model analysis for the 3 networks |
La和Na越小,管道故障的影响范围越小,管网可靠性越高.L/V越小,单位长度管道内阀门数量越多,故障越容易控制在局部范围,管网可靠性越高.分析结果显示管网可靠性排序为GW2>GW3>GW1.单元完整覆盖管网,总体呈现均匀分布,所以,单元故障与随机攻击的效果类似.上述SV图分析结果符合PDG模型下的分析结论,与随机攻击下PDG结构的健壮性一致,验证了PDG模型对可靠性评估的价值.
4 结论提出一种新的管网拓扑模型——PDG模型作为供水管网可靠性分析工具,并基于此模型提出了管网可靠性分析方法.针对3个城市供水管网PDG模型,运用复杂网络理论进行管网的结构测度和鲁棒性分析,得出以下结论:
1) 供水管网的PDG模型具有明显的无标度特性,突破了节点-连边经典网络模型的局限性,能更好地表征在发生故障或者遭受攻击时管网性能受到的影响.
2) 不同管网在不同的攻击策略下结构变化规律呈现较强的相似性,都会经过初始期、分裂期和崩溃期3个阶段.不同的攻击策略下供水管网进入分裂期和崩溃期的进程差异明显.基于节点度的攻击策略对管网结构的影响最大,基于节点介数中心性其次,随机攻击最小.高度连接的管线应作为系统维护的重点.
3) 结构测度与鲁棒性分析相结合,是一种有效地评价管网可靠性的方法.谱隙在度量供水管网连通性时区分度较好,而管网进入分裂期时的去点率可作为衡量其鲁棒性的重要指标.
本文提出的PDG模型分析方法,可用于比较和优选供水管网设计和运维的不同方案.该方法以及用于对比的基于SV图的经典可靠性分析方法,均侧重对管网结构和连通性的分析,属于解析法范畴,难以细致体现在各种攻击策略中压力和流量对需求的满足程度.针对此局限,后续研究可将解析法和模拟法相结合,以水力模型为辅助工具,将PDG模型与原始管网关联起来,进一步分析攻击对管网流量、压力等参数的影响,发展更为细致的攻击策略和评价指标,更为全面地分析供水管网的可靠性.
| [1] |
GUPTA R, BHAVE P R. Reliability-analysis of water-distribution systems[J]. Journal of Environmental Engineering, 1994, 120(2): 447-461. DOI:10.1061/(ASCE)0733-9372(1994)120:2(447) |
| [2] |
SHA Z, PANCHAL J H. Towards the design of complex evolving networks with high robustness and resilience[J]. Procedia Computer Science, 2013, 16: 522-531. DOI:10.1016/j.procs.2013.01.055 |
| [3] |
WAGNER J M, SHAMIR U, MARKS D H. Water distribution reliability: analytical methods[J]. Journal of Water Resources Planning & Management, 1988, 114(3): 253-275. DOI:10.1061/(ASCE)0733-9496(1988)114:3(253) |
| [4] |
WAGNER J M, SHAMIR U, MARKS D H. Water distribution reliability: simulation methods[J]. Journal of Water Resources Planning & Management, 1988, 114(3): 276-294. DOI:10.1061/(ASCE)0733-9496(1988)114:3(276) |
| [5] |
QUIMPO R G, SHAMSI U M. Reliability-based distribution system maintenance[J]. Journal of Water Resources Planning and Management, 1991, 117(3): 321-339. DOI:10.1061/(ASCE)0733-9496(1991)117:3(321) |
| [6] |
KANSAL M L, KUMAR A, SHARMA P B. Reliability analysis of water distribution systems under uncertainty[J]. Reliability Engineering and System Safety, 1995, 50(1): 51-59. DOI:10.1061/(ASCE)0733-9372(1995)121:9(674) |
| [7] |
WALSKI T M. Practical aspects of providing reliability in water distribution systems[J]. Reliability Engineering & System Safety, 1993, 42(1): 13-19. DOI:10.1016/0951-8320(93)90050-9 |
| [8] |
JUN H, LOGANATHAN G V, DEB A K, et al. Isolating subsystems in a water distribution network[C]// World Water and Environmental Resources Congress. 2004: 1-8. DOI: 10.1061/40737(2004)466.
|
| [9] |
STROGATZ S H. Exploring complex networks[J]. Nature, 2001, 410(6825): 268. DOI:10.1038/410268a0 |
| [10] |
YAZDANI A, OTOO R A, JEFFREY P. Resilience enhancing expansion strategies for water distribution systems:A network theory approach[J]. Environmental Modelling & Software, 2011, 26(12): 1574-1582. DOI:10.1016/j.envsoft.2011.07.016 |
| [11] |
YAZDANI A, JEFFREY P. Applying network theory to quantify the redundancy and structural robustness of water distribution systems[J]. Journal of Water Resources Planning and Management, 2012, 138(2): 153-161. DOI:10.1061/(ASCE)WR.1943-5452.0000159 |
| [12] |
HAWICKK A. Water distribution network robustness and fragmentation using graph[C]// Proc Int Conf on Water Resource Management (AfricaWRM 2012). IASTED, 2012: 304-310. DOI: 10.2316/P.2012.762-037.
|
| [13] |
WATTSD J, STROGATZ S H. Collective dynamics of 'small-world' networks[J]. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 |
| [14] |
BOCCALETTI S, BIANCONI G, CRIADO R, et al. The structure and dynamics of multilayer networks[J]. Physics Reports, 2014, 544(1): 1-122. DOI:10.1016/j.physrep.2014.07.001 |
| [15] |
DE CORTE A, SÖRENSEN K. HydroGen: An artificial water distribution network generator[J]. Water Resources Management, 2014, 28(2): 333-350. DOI:10.1007/s11269-013-0485-y |
| [16] |
ESTRADA E. Network robustness to targeted attacks. The interplay of expansibility and degree distribution[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2006, 52(4): 563-574. DOI:10.1140/epjb/e2006-00330-7 |
| [17] |
MALLIAROSF D, MEGALOOIKONOMOU V, FALOUTSOS C. Estimating robustness in large social graphs[J]. Knowledge and Information Systems, 2015, 45(3): 1-34. |
| [18] |
FIEDLER M. Algebraic connectivity of graphs[J]. Czechoslovak Mathematical Journal, 1973, 23(2): 298-305. DOI:10.1007/s10115-014-0810-7 |
| [19] |
ZHOU H, BABAEI A, MAO S, et al. Algebraic connectivity of degree constrained spanning trees for FSO networks[C]// Communications (ICC). 2013 IEEE International Conference on IEEE, 2013: 5991-5996. DOI: 10.1109/ICC.2013.6655558.
|
| [20] |
ALBERT R, JEONG H, BARABASI A L. Internet: Diameter of the world-wide web[J]. Nature, 1999, 401(6749): 130-131. DOI:10.1038/43601 |
| [21] |
ALBERT R, JEONG H, BARABASI A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406(6794): 378-382. DOI:10.1038/35019019 |
| [22] |
YAZDANI A, JEFFREY P. Complex network analysis of water distribution systems[J]. Chaos, 2011, 21(1): 016111. DOI:10.1063/1.3540339 |
| [23] |
BRUNEAU M, CHANG S E, EGUCHI R T, et al. A framework to quantitatively assess and enhance the seismic resilience of communities[J]. Earthquake Spectra, 2003, 19(4): 733-752. DOI:10.1193/1.1623497 |
| [24] |
HOLME P, KIM B J, YOON C N, et al. Attack vulnerability of complex networks[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2002, 65(5 Pt 2): 056109. DOI:10.1103/PhysRevE.65.056109 |
| [25] |
BARTHELEMY M. Betweenness centrality in large complex networks[J]. The European Physical Journal B-Condensed Matter and Complex Systems, 2004, 38(2): 163-168. DOI:10.1140/epjb/e2004-00111-4 |
 2018, Vol. 50
2018, Vol. 50


