实现管网优化调度能够节约大量供水能耗,全面提高供水的安全性和可靠性,但调度的重要前提是获得高精度的日用水量预测值.鉴于日用水量的非线性特征,学者们以主要影响因素和相关日用水量为输入,采用非线性映射能力较强的神经网络[1-3]建模,但是神经网络存在参数较多,训练易陷入局部最优和过拟合等问题.Msiza等[4]根据主要影响因素和相关日用水量,利用参数较少(3个)和预测能力更强的支持向量机(SVM)建模.柳景青[5]引入改进粗糙集算法深入分析了不同季节的日用水量主要影响因素,进一步提高了基于SVM模型的预测精度.然而,传统采用网格交叉验证法确定SVM模型参数耗时较长,并且优化的参数取决于网格的划分,有较强的主观性.Huang等[6]利用传统遗传算法(GA)优化SVM的参数,但其未解决GA全局搜索能力较差的问题,难以找到较优参数.为此,本文在利用粗糙集和自相关系数法客观确定模型输入参数的基础上,引入参数更少(2个)和计算速度更快的最小二乘支持向量机(LSSVM)来建模,并利用寻优能力较强的差分进化算法对模型参数进行优化,全面提高模型的建模速度和预测精度.
1 函数估计的LSSVM算法[7]对于训练样本{xk, yk}k=1N,输入xk∈ Rn,输出yk∈R.
目标函数为
| $ \begin{array}{*{20}{c}} {{J_1}\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{e}}} \right) = \mu {E_W} + \zeta {E_D} = \frac{\mu }{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w + }}\frac{1}{2}\zeta \sum\limits_{k = 1}^N {e_k^2} ,}\\ {{\rm{s}}.{\rm{t}}.{y_k} = {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{\mathit{\boldsymbol{x}}_k}} \right) + b + {e_k},k = 1, \cdots ,N.} \end{array} $ | (1) |
式中:权矢量w∈ Rnf,误差ek∈ R,μ和ζ为参数, 核函数φ(xk): Rn→ Rnf,b为偏置.
为求解最小值,构造函数
| $ L = {J_1}\left( {\mathit{\boldsymbol{w}},\mathit{\boldsymbol{e}}} \right) - \sum\limits_{k = 1}^N {{\alpha _k}\left\{ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{\mathit{\boldsymbol{x}}_k}} \right) + b + {e_k} - {y_k}} \right\}} . $ | (2) |
式中αk为拉格朗日系数.
设γ=ζ/μ,对式(2)求偏导:
| $ \left\{ \begin{array}{l} \frac{{\partial L}}{{\partial \mathit{\boldsymbol{w}}}} = 0 \to \mathit{\boldsymbol{w}} = \sum\limits_{k = 1}^N {{\alpha _k}\varphi \left( {{\mathit{\boldsymbol{x}}_k}} \right)} ;\\ \frac{{\partial L}}{{\partial b}} = 0 \to \sum\limits_{k = 1}^N {{\alpha _k}} = 0;\\ \frac{{\partial L}}{{\partial {e_k}}} = 0 \to {\alpha _k} = \gamma {e_k},k = 1, \cdots ,N;\\ \frac{{\partial L}}{{\partial {\alpha _k}}} = 0 \to {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{\mathit{\boldsymbol{x}}_k}} \right) + b + {e_k} - {y_k} = 0,k = 1, \cdots ,N. \end{array} \right. $ | (3) |
消去w和e, 得
| $ \left[ {\begin{array}{*{20}{c}} 0&{{\bf{1}}_v^{\rm{T}}}\\ {{{\bf{1}}_v}}&{\mathit{\Omega } + \frac{1}{\gamma }\mathit{\boldsymbol{I}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} b\\ \mathit{\boldsymbol{\alpha }} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0\\ \mathit{\boldsymbol{y}} \end{array}} \right]. $ | (4) |
式中:y =[y1, …, yn]T, 1 v=[1, …, 1]T, α =[α1, …, αn]T, I为N×N的单位阵, Ωkl=φ(xk)Tφ(xl)=K(xk, xl), k, l=1, …, N.
求出α和b,则采用径向基核函数的LSSVM的表达式为
| $ y\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{k = 1}^N {{\alpha _k}K\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_k}} \right) + b} . $ | (5) |
式中K(x, xk)=exp{-‖x-xk‖2/σ2.
因此,建模仅需确定σ和γ两个参数.
2 差分进化算法(DE)优化模型参数DE[8]是一种利用种群个体间的合作和竞争实现优化搜索的算法.通过采用差分变异操作和竞争生存策略,该算法能够对优化空间实现全局搜索.由于DE算法的搜索性能主要取决于差分缩放因子F和交叉概率CR的取值,采用根据个体的目标值自适应调整参数的策略,以获得更好的优化结果.
DE算法的种群由NP个个体组成,每个个体由优化参数γ和σ组成.DE算法由编码、变异、交叉和选择等操作组成.
1) 编码
γ和σ采用实数编码,取值范围[9]:γ∈[0.01, 50],σ∈[0.01, 50].
2) 变异
对于G代第i个个体,在[0, 1]区间内产生一个随机实数Fi, G,G代第i个个体中的第j个优化参数pi, Gj(j=1, 2)经过变异,得到相应的变异参数
| $ v_{i,G + 1}^j = p_{{r_1},G}^j + {F_{i,G}}\left( {p_{{r_2},G}^j - p_{{r_3},G}^j} \right). $ | (6) |
式中:r1、r2、r3为[1, NP]区间内随机产生的互不相同的整数,分别表示个体的编号,并且r1≠r2≠r3≠i;G为代数;Fi, G为缩放因子,控制着差分向量(pr2, Gj-pr3, Gj)的缩放.
3) 交叉
优化参数pi, Gj和变异参数vi, G+1j根据式(7)进行混合,产生试验参数ui, G+1j(j=1, 2):
| $ u_{i,G + 1}^j = \left\{ \begin{array}{l} v_{i,G + 1}^j,\;\;{\rm{rand}} \le C{R_{i,G}}\;或\;i = {\rm{rand}}n\left( 2 \right);\\ p_{i,G}^j,\;\;\;\;其他. \end{array} \right. $ | (7) |
式中:rand为在[0, 1]区间内随机产生的一个数;CRi, G为G代第i个个体的交叉率; randn(2)为[1, 2]区间内产生的一个随机正整数,以保证至少一个优化参数会发生变异.
4) 选择
计算优化参数pi, Gj和试验参数ui, G+1j(j=1, 2)对应的目标函数,采用贪婪的选择模式
| $ p_{i,G + 1}^j = \left\{ \begin{array}{l} u_{i,G + 1}^j,f\left( {u_{i,G + 1}^1,u_{i,G + 1}^2} \right) < f\left( {p_{i,G}^1,p_{i,G}^2} \right);\\ p_{i,G}^j,f\left( {u_{i,G + 1}^1,u_{i,G + 1}^2} \right) \ge f\left( {p_{i,G}^1,p_{i,G}^2} \right). \end{array} \right. $ | (8) |
为了获得更好的个体,需在贪婪选择前对F和CR进行自适应调整.
对于G代第i个个体,若根据Fi, G和CRi, G的组合得到试验参数的目标值小于优化参数对应的目标值,则G+1代第i个个体的Fi, G+1和CRi, G+1保持不变;否则,在取值范围内重新随机产生Fi, G+1和CRi, G+1.具体如下:
| $ {F_{i,G + 1}} = \left\{ \begin{array}{l} {F_{i,G}},f\left( {u_{i,G + 1}^1,u_{i,G + 1}^2} \right) \le f\left( {p_{i,G}^1,p_{i,G}^2} \right);\\ {F_{\min }} + {\rm{rand}} \times \left( {{F_{\max }} - {F_{\min }}} \right),\;\;\;\;\;其他. \end{array} \right. $ | (9) |
式中Fmin、Fmax分别为F取值的下限和上限.
| $ C{R_{i,G + 1}} = \left\{ \begin{array}{l} C{R_{i,G}},f\left( {u_{i,G + 1}^1,u_{i,G + 1}^2} \right) \le f\left( {p_{i,G}^1,p_{i,G}^2} \right);\\ C{R_{\min }} + {\rm{rand}} \times \left( {C{R_{\max }} - C{R_{\min }}} \right),\;\;\;\;其他. \end{array} \right. $ | (10) |
式中CRmin、CRmax分别为CR取值的下限和上限.
3 基于SADELSSVM的日用水量建模和预测 3.1 模型的输入参数分析 3.1.1 主要影响因素分析一般来说,日用水量的影响因素主要是最高温度、平均温度、最低温度、星期量、阴晴量和降雨量等因素.为了进一步确定主要影响因素,采用善于处理不精确、不相容数据的基于权值累计评价的可变精度粗糙集算法.通过引入变精度,使算法具有较好的整体信息评价能力和容错性;通过采用权值累计评价,使算法客观评价主影响因素,较好地解决分析不同长度序列可能得到不同主要影响因素的不足.
利用浙江某城市2003年—2006年的日用水量及相关天气数据,采用改进粗糙集算法分析了不同季节的主要影响因素,过程详见文献[5].分析结果为:春、冬季日用水量的主要影响因素为相对湿度、阴晴量、星期量和平均温度,而夏、秋季日用水量的主要影响因素为相对湿度、阴晴量、星期量和最高温度.各季日用水量都删除了部分影响因素,这些因素虽然也重要,但它们与主要影响因素相关,因此可被替代.比如:最低温度、最高温度与平均温度有一定相关性,阴晴量则可部分表示降雨量.因此,计算结果是合理的.
3.1.2 序列相关性分析采用自相关系数法确定序列数据间的相关性,具体过程如下.
日用水量序列dt(t=1, 2, …, T)的自相关系数为
| $ {c_h} = \frac{{\sum\limits_{t = 1}^{T - h} {\left( {{d_t} - \bar d} \right)\left( {{d_{t + h}} - \bar d} \right)} }}{{\sum\limits_{t = 1}^T {{{\left( {{d_t} - \bar d} \right)}^2}} }}. $ | (11) |
式中:
根据2003年—2006年的序列,计算得到|c7| =0.831,其他的|ch| <0.5.
3.2 日用水量建模和预测鉴于四季的主要影响因素不尽相同,为了便于建模和预测,输入取各季主要影响因素的合集,即相对湿度、阴晴量、星期量、平均温度和最高温度, 其中星期量∈[1, 8],节假日的星期量取8,阴晴量∈[1, 8].考虑到序列的相关性,输入增加取预测日前第7天日用水量.
将2007年—2008年的日用水量数据分为367组数据,其中2007年1月1日—12月26日360组是训练验证集,2007年12月27日—2008年1月2日7组(包括工作日和周末日)为预测集.为了客观评价模型参数,将360组数据6等分,进行6折交叉验证计算(即每次选5份数据训练LSSVM,用1份验证LSSVM,进行每次选取不同验证集的6次验证),各个体的目标值计算方法如下:
| $ f\left( {\gamma ,\sigma } \right) = {\left( {\sum\limits_{m = 1}^{6} {\sum\limits_{q = 1}^{60} {\frac{1}{{60}}{{\left( {{F_{mq}} - {Y_{mq}}} \right)}^2}} } } \right)^2}. $ | (12) |
式中:γ、σ为个体中对应的LSSVM参数;Fmq表示第m次验证中以验证集第q组数据为LSSVM输入计算得到的预测值;Ymq表示第m次验证中验证集第q组输入数据对应的实际日用水量.
日用水量建模的过程如下:
1) 设置SADE算法最大进化代数MAX为100,赋值代数G为1,取种群的个体数NP=50,随机产生第i个实数编码的个体(γi, σi)以及与其对应的Fi, G和CRi, G (i=1, 2, …, NP).
2) 利用交叉验证法计算种群个体的目标值(对训练验证集中的训练数据和验证的输入数据归一化预处理,并反预处理预测结果).
3) 对各个体中的优化参数进行变异和交叉,得到相应试验参数,并判断各试验参数是否已超出取值范围:若试验参数小于0.01,试验参数取0.01;若大于50,则取50.
4) 根据试验参数,同样利用交叉验证法计算其目标函数值,与对应优化参数的目标值对比后,通过选择得到新种群及其个体目标值.根据选择结果,对种群第i个(i=1, …, NP)个体的Fi, G和CRi, G进行自适应调整.
5) 判断G是否等于最大进化代数:若是,输出最小目标值对应的最优参数,计算结束;若否,G=G+1,转到步骤3).
为验证SADE算法的寻优能力,将其与自适应遗传算法(SAGA)和传统DE算法进行对比,3种算法都采用相同的寻优范围和目标函数.传统DE算法的F和CR分别取0.7和0.9(根据文献[10]的结论并进行试算),其他参数和SADE算法一样.自适应遗传算法(SAGA)的个体取50个,个体中γ和σ都采用实数编码,最大进化代数取100,采用轮盘赌法和两位交叉方式,采用自适应交叉和变异操作[11](高目标值的个体具有更大的交叉和变异概率),每代保留种群最优个体.
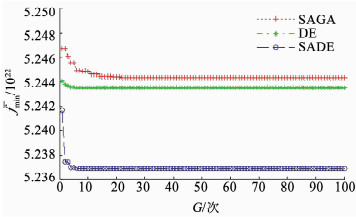
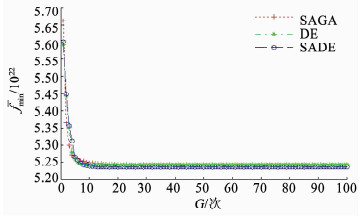
由于SAGA、SADE和DE算法的个体是随机产生的,每个算法都在配置为CPU Intel Core i5 1.8G、4G DDR内存的计算机上运行5次,以更好地验证算法的寻优能力.5次优化计算得到的最小目标值平均值fmin和平均目标值平均值favg详见图 1、2.可以看出,SADE不仅具有最强的全局寻优能力(5次中最多在15代找到最优的个体,最优个体目标值也最小),而且具有最快的群体平均进化速度,从第7代起已获得比DE和SAGA更小的favg;DE算法也具有较强的全局寻优能力(5次中最多在25代找到最优的个体,最优个体目标值仅次于SADE),并且具有较快的群体平均进化速度,从第7代起已获得比SAGA更小的favg;SAGA则具有最差的全局寻优能力(5次中最多在50代才找到最优个体,最优个体的目标值也最大),并且群体平均进化速度最慢,7代后的favg都为最大.
|
图 1 最小目标值平均值对比 Figure 1 Comparison of the mean of minimum objective values among three algorithms |
|
图 2 平均目标值平均值对比 Figure 2 Comparison of the mean of average objective values among three algorithms |
取5次计算中最小目标值的对应参数为每个算法优化得到的最优参数,SADE、DE和SAGA算法得到的最优参数分别为(0.435 6,1.284 7)、(0.318 5,1.695 1)和(0.671 4,2.192 3).分别用各最优参数对LSSVM的参数赋值,利用预处理后的360组训练测试集训练LSSVM模型,然后模型根据预处理后的预测集输入数据对7日用水量进行预测,在对预测结果反预处理后,得到图 3所示的结果.

|
图 3 日用水量预测对比 Figure 3 Comparison of daily water demand forecasting among three models |
采用绝对相对误差eAPE和平均绝对相对误差eMAPE来评价各模型的预测结果:
| $ {e_{{\rm{APE}}}} = \left| {\frac{{{Y_s} - {F_s}}}{{{Y_s}}}} \right|, $ | (13) |
| $ {e_{{\rm{MAPE}}}} = \frac{1}{S}\sum\limits_{s = 1}^S {\left| {\frac{{{Y_s} - {F_s}}}{{{Y_s}}}} \right|} . $ | (14) |
式中:Fs为模型对第s天日用水量的预测值,Ys为第s天的实际日用水量, S为预测总天数.
对于2007年12月27日—2008年1月2日的7日用水量,基于SADELSSVM模型预测的绝对相对误差分别为1.4%、1.6%、4.2%、5.0%、0.5%、0.2%、3.4%,绝对相对误差的最大值为5.0%,平均绝对相对误差为2.33%.基于DELSSVM模型预测7日用水量的绝对相对误差分别为1.7%、1.9%、7.3%、5.9%、1.8%、2.1%、5.1%,绝对相对误差的最大值为7.3%,平均绝对相对误差为3.69%.基于SAGALSSVM模型预测7日用水量的绝对相对误差分别为1.0%、1.1%、8.2%、7.5%、0.9%、2.0%、5.5%,绝对相对误差的最大值为8.2%,平均绝对相对误差为3.74%.由于12月30日用水量与以前相差较大,基于SADELSSVM模型、基于DELSSVM模型和基于SAGALSSVM模型对该日预测误差都较大,分别为5.0%、5.9%和7.5%.对于3个算法,SADE算法具有最强的全局寻优能力,DE算法具有较强的全局寻优能力,因此,基于SADELSSVM模型预测误差最小,基于DELSSVM模型预测误差较小.12月29日和1月2日与以前用水量相差不大,SADE算法仍能够找到较优的模型参数,因此,基于SADELSSVM模型预测误差仅为4.2%、3.4%.但限于DE和SAGA算法的寻优能力,基于DELSSVM模型和基于SAGALSSVM模型的参数与基于SADELSSVM模型的参数有一定偏差,因此,两模型对12月29日和1月2日预测的绝对相对误差也较大,预测结果分别为7.3%、5.1%和8.2%、5.5%.
在季节变化时,日用水量一般会有较大变化,预测难度较大,因此,分别利用以上3个模型预测该城市2008年四季改变后一周的日用水量(3月1日—7日、6月1日—7日、9月1日—7日、12月1日—7日),以进一步验证本文提出模型的有效性,得到的预测结果见表 1.可以看出,对于28日中每一天的预测结果,基于SADELSSVM模型预测精度最高,基于DELSSVM模型预测精度第二,基于SAGALSSVM模型预测精度则最差.基于SADELSSVM模型预测的平均绝对相对误差为3.56%,绝对相对误差的最大值为6.7%(9月1日).基于DELSSVM模型预测的平均绝对相对误差为4.07%,绝对相对误差的最大值为7.1%(6月1日).基于SAGALSSVM模型预测的平均绝对相对误差为4.49%,绝对相对误差的最大值为8.3%(6月1日).由于3月1日、3月2日、6月1日、6月2日、9月1日、9月2日、12月1日和12月2日与以前的日用水量相差较大,3个模型对8日的预测误差都较大,但是具有较强全局寻优能力的SADE算法仍能根据历史数据搜索到较优参数,因此,基于SADELSSVM模型对该8日的预测误差较小.由于DE算法寻优能力较差,SAGA算法寻优能力最差,基于DELSSVM模型对该8日的预测误差较大,基于SAGALSSVM模型对该8日的预测误差最大.
| 表 1 绝对相对预测误差对比 % Table 1 Comparison of absolute relative error among three models |
综上,基于SADELSSVM模型具有最强的预测能力,基于DELSSVM模型具有较强的预测能力,基于SAGALSSVM模型则具有最差的预测能力.
4 结语SADE算法根据个体进化结果自适应调整每个个体的差分向量缩放因子和交叉概率,较好地解决了传统DE算法两参数的确定问题,而且全面提高了算法的全局搜索能力和收敛速度.分析结果验证了SADE算法具有更强全局寻优能力和更快收敛速度,也验证了基于SADELSSVM模型具有更强的预测能力.
| [1] |
BABEL M S, SHINDE V R. Identifying prominent explanatory variables for water demand prediction using artificial neural networks: A case study of Bangkok[J]. Water Resources Management, 2011, 25(6): 1653-1676. DOI:10.1007/s11269-010-9766-x |
| [2] |
袁一星, 兰宏娟, 赵洪宾, 等. 城市用水量BP网络预测模型[J]. 哈尔滨建筑大学学报, 2002, 35(3): 56-58. YUAN Yixing, LAN Hongjuan, ZHAO Hongbin, et al. BP model for forecasting urban water consumption[J]. Journal of Harbin University of C. E. & Architecture, 2002, 35(3): 56-58. |
| [3] |
王亮, 汪震, 岳琳. 基于粒子群优化算法的城市日用水量预测模型[J]. 中国给水排水, 2007, 23(7): 89-93. WANG Liang, WANG Zhen, YUE Lin. Urban daily water consumption forecasting model based on particle swarm optimization[J]. China Water & Wastewater, 2007, 23(7): 89-93. DOI:10.3321/j.issn:1000-4602.2007.07.023 |
| [4] |
MSIZA S, NELWAMONDO F, MARWALA T. Water demand prediction using artificial neural networks and support vector regression[J]. Journal of Computers, 2008, 3(11): 1-8. DOI:10.4304/jcp.3.11.1-8 |
| [5] |
柳景青. 调度时用水量预测的系统理论方法及应用研究[D]. 浙江: 浙江大学, 2005. LIU Jingqing. Study on forecasting model of hourly water consumption for optimal operation[D]. Zhejiang: Zhejiang University, 2005. http://cdmd.cnki.com.cn/article/cdmd-10335-2005086960.htm |
| [6] |
HUANG C L, WANG C J. A GA-based feature selection and parameters optimization for support vector machines[J]. Expert Systems with Applications, 2006, 31(2): 231-240. DOI:10.1016/j.eswa.2005.09.024 |
| [7] |
SUYKENS J A K, GESTEL V T, BRABANTER D J, et al. Least squares support vector machines[M]. Singapore: World Scientific, 2002.
|
| [8] |
STORN R, PRICE K V. Differential evolution-a simple and efficient heuristic for global optimization over continuous space[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [9] |
GESTEL V T, SUYKENS J A K, BAESENS B, et al. Benchmarking least squares support vector machine classifiers[J]. Machine Learning, 2004, 54(1): 5-32. DOI:10.1023/B:MACH.0000008082.80494.e0 |
| [10] |
STORN R, PRICE K V, LAMPINEN J. Differential evolution: A practical approach to global optimization[M]. Berlin: Springer, 2005.
|
| [11] |
SRINIVAS M, PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on System Man and Cybernatics, 1994, 24(4): 656-667. DOI:10.1109/21.286385 |
 2018, Vol. 50
2018, Vol. 50


