2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. School of Engineering, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. School of Engineering, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK
FLNG (floating liquefied natural gas)和LNGC (liquefied natural gas carrier)的近靠卸载,通常仅相距4~10 m.两船构成的多浮体系统引发复杂的水动力干扰作用,为准确预报两船的运动带来困难.双船运动的准确预报主要面临两大问题—多浮体水动力干扰和间隙水域的黏性问题,而遮蔽效应的研究也从以上两大问题着手.
对于早期的多浮体间的水动力干扰问题,Ohkusu等[1]首先采用二维切片理论分析了两船旁靠时的水动力影响.Van Oortmerssen[2]采用三维线性绕射理论进行了进一步探究.基于早期的研究,Choi和Hong[3]采用高阶边界元法计算多浮体间水动力干扰.Hong和Kim[4]从数值和试验的角度研究了两船旁靠系统在横浪和迎浪下的一阶运动和二阶波浪力,发现横浪下两船运动的遮蔽效应十分明显.许鑫等[5]研究了三个驳船旁靠进行浮托作业时的水动力干扰和计算网格的收敛性,并与试验对比验证了算法的可靠性.João Pessoa和Nuno Fonseca等[6]考虑连接器的作用并研究了FLNG旁靠的全耦合模型,分析了两船的相对运动和系泊缆及防碰垫上的载荷,并通过模型试验验证数值算法的可靠性.
对于黏性的影响,众多学者在势流的基础上提出了修正的方法,使得数值结果更符合实际.2001年Huijsmans[7]首次提出刚性盖(rigid lid)理论,有效抑制波面运动.为了允许产生波面运动,Newman[8]提出了柔性盖的方法,采用切比雪夫多项式拟合间隙区域的波面,通过设定一个线性阻尼因子来降低谐振振幅.由于以上方法均使得流场引入了外界扰动,陈小波[9]提出了阻尼盖理论,通过在动量方程中引入阻尼力,推导出带阻尼因子“epsilon”的自由面条件并施加在两船间隙水面中,此方法从流场能量耗散的机理上抑制波面的谐振.
之前的研究大多关注两船受风标效应时迎浪条件下的运动,因此,针对不同浪向(斜浪)下的研究相对较少.其中,早期研究的两船相距较远,不用考虑间隙水体的黏性效应.例如,Fang和Chen[10]采用纯三维线性势流理论,计算了不同斜浪下两船(D/B= 2,D为间隙宽度,B为船宽)固定和自由漂时的相对运动和间隙波面共振,分析发现大船的遮蔽效应对间隙波面共振影响显著.Kim[11]采用非黏性Rankine源方法计算了不同浪向下两船(D/B=2)的运动响应和波浪场,分析了两船遮蔽效应对垂荡和纵摇的影响,并发现双船对斜浪的反射能力较之单船更强.对于小间隙旁靠,Shivaji[12]采用阻尼盖的方法,从时域的角度分析了近靠的两驳船(D/B=0.2)在大波陡的横浪与斜浪下非线性运动的遮蔽效应,考虑了F-K力和静水恢复力在瞬时湿表面的积分.
本文采用数值和模型试验相结合的方法,较为全面地研究了不同浪向对小间隙液面共振、FLNG和LNGC两船体运动以及二阶平均漂移力的影响,以此分析了水动力遮蔽现象.对比之前的研究,主要针对小间距(D/B<0.2)旁靠的两船水动力问题进行研究,考虑浪向的变化对阻尼盖[9]施加的影响.同时,着重分析由体积不同的两船所引发的斜浪下的遮蔽效应,分析了较为危险的横向运动,可为FLNG的工程实践提供重要参考.
1 数值方法基于HYDROSTAR软件,采用人工自由面阻尼修正后的三维频域势流理论进行双船运动的计算.通过试验与数值的对比选取适当的自由面阻尼ε,并基于修正后的参数计算波面升高和船体运动,进而采用中场法求解平均漂移力.
为了描述两船的运动和受力,首先建立坐标系,分别为两船随体坐标系ok-xkykzk(k=A, B)和空间固定的大地坐标系o-xyz.随体坐标系中,FLNG的坐标下标为A,LNGC的坐标下标为B,如图 1所示.其中x轴指向船首,y轴指向船身左舷,z轴垂直向上.坐标系的原点都在静水面上.

|
图 1 坐标系的设定 Figure 1 Definition of coordinate systems |
人工阻尼盖法[9]通过在动量方程中添加阻尼力项,改变自由面边界条件并施加在两船之间的自由面网格上,最终修正无黏性势流理论.这种方法类似于添加线性横摇附加阻尼,来模拟舭龙骨在船体横摇中引起的水体能量耗散,从而减小谐摇时的峰值,而对其他频率下的运动影响很小.
在动量方程中引入黏性力项
| $ {\mathit{\boldsymbol{f}}_{{\rm{dmp}}}}{\rm{ = - }}\mathit{\mu }\mathit{\boldsymbol{v}}{\rm{.}} $ | (1) |
式中:μ为大于零的阻尼系数,v为流场中某点流体运动速度.修正后的动量方程为
| $ \mathit{\boldsymbol{v}}\nabla {\rm{\cdot}}\mathit{\boldsymbol{v}}{\rm{ + }}\frac{{\partial \mathit{\boldsymbol{v}}}}{{\partial \mathit{t}}}{\rm{ = - }}\mathit{\mu }\mathit{\boldsymbol{v}}{\rm{ + }}\mathit{\boldsymbol{f}}{\rm{ + }}\frac{{\rm{1}}}{\mathit{\rho }}\nabla \mathit{p}{\rm{.}} $ | (2) |
式中:f为惯性力项,ρ为流体密度,p为流场中某点压强.
由于修正后的动量方程仍满足Kelvin定理,为无旋场,可用速度势Φ描述.那么间隙中的波面升高可用下式表达:
| $ \mathit{\eta }{\rm{ = - }}\frac{{\rm{1}}}{\mathit{g}}\left( {\frac{{\partial \mathit{\Phi }}}{{\partial \mathit{t}}}{\rm{ + }}\mathit{\mu \Phi }} \right){\rm{.}} $ | (3) |
式中g为重力加速度.在外液面上采用传统势流的自由面条件,而间隙液面上的自由面条件变为
| $ \begin{array}{l} - \left( {{\rm{1 + i}}\mathit{\varepsilon }} \right){\mathit{\omega }^{\rm{2}}}{\mathit{\varphi }_{\rm{m}}}{\rm{ + }}\mathit{g}\frac{\partial }{{\partial \mathit{z}}}{\mathit{\varphi }_{\rm{m}}}{\rm{ = 0, }}\\ \;\;\;{\rm{(}}\mathit{m}{\rm{ = 1, 2, }} \cdots {\rm{12;}}\mathit{\varepsilon }{\rm{ = }}\frac{\mathit{\mu }}{\mathit{\omega }}{\rm{)}}{\rm{.}} \end{array} $ | (4) |
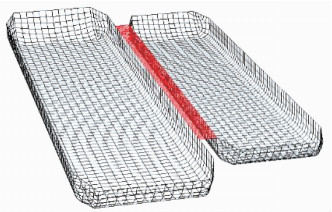
其中ω为频率,φm为两船12个广义自由度下规范化的速度势[13],ε取值0~1使得波面升高的计算值与试验相匹配.考虑到仅在两船间隙中液面共振最剧烈,本文中阻尼盖覆盖FLNG和LNGC近靠间隙内的液面,长度为LNGC平行中体长,如图 2红色所示.最后,通过试验测得的间隙中点的波面升高RAO来选取合适的阻尼因子.
|
图 2 两船湿表面的板单元模型 Figure 2 Wet surface panel models of two vessels |
采用人工阻尼盖法修正双船辐射和绕射问题的定解条件,采用格林函数法求解边界积分方程和速度势.通过波浪力在平均湿表面(图 2)的积分,获取运动方程中的附加质量阻尼系数和波浪力等参数,具体理论参考文献[13].两船频域内的运动方程与单船的类似,求解时由单浮体的6×6矩阵方程变为12×12的方程,即
| $ \left[ {{\rm{ - }}{\mathit{\omega }^{\rm{2}}}\left( {\mathit{\boldsymbol{M}}{\rm{ + }}\mathit{\boldsymbol{A}}{\rm{}}} \right){\rm{ - i}}\mathit{\omega }\left( {\mathit{\boldsymbol{B}}{\rm{ + }}\mathit{\boldsymbol{B'}}} \right){\rm{ + }}\mathit{\boldsymbol{K}}} \right]\mathit{\boldsymbol{x}}{\rm{ = }}\mathit{\boldsymbol{F}}{\rm{.}} $ | (5) |
式中:ω为频率,M为船体质量阵,A和B为附加质量和兴波阻尼阵; B'为黏性阻尼阵; K为静水恢复力阵; x为双船的12自由度位移; F为波浪激励力.
对于二阶平均漂移力的计算,由于近场法对网格密度要求较高,计算效率低,而远场法无法计算单个浮体的二阶力,选用中场法[14]计算各浪向下的平均漂移力,既保证了收敛性又提高了精度.通过对每个浮体设置控制面,中场法将流体压力积分面从船体湿表面转移到控制面上.
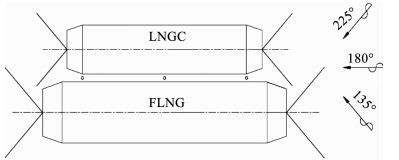
2 模型试验为了选取合适的自由面阻尼ε并验证数值结果的准确性,开展了模型试验.本次试验在上海交通大学深水试验池中进行(缩尺比为1:60),试验水深5 m.FLNG与LNGC两船的船体参数如表 1.试验中FLNG与LNGC两船间隔6 m(模型值0.1 m)并列放置,如图 3所示.两船采用沿45°布置的软刚度弹簧进行水平系泊,用以抵消二阶慢漂运动并避免对波频运动的干扰.试验中在两船间隙中线处布置3个浪高仪测量波浪升高时历,纵向位置分别为间隙的首尾和中点处,如图 3圆圈所示.试验中设置3个浪向,可见当处于135°浪向时,大船迎浪遮蔽小船;225°浪向时,小船迎浪遮蔽大船.
| 表 1 FLNG和LNGC主尺度和参数 Table 1 Principal particulars of the FLNG and LNGC |
|
图 3 模型试验布置 Figure 3 Layout of model tests |
试验内容包含横摇衰减试验和不规则波试验两部分.衰减试验中,一船固定,测量另一船做横摇自由衰减的运动时历.通过衰减试验可校核模型惯量参数,并根据赵文华[15]提出的理论方法,由无因次阻尼系数γ计算横摇黏性阻尼B',衰减分析结果见表 2.
| 表 2 横摇衰减试验分析 Table 2 Analysis of roll decay tests |
不规则波试验中,测量两船在135°、180°和225°白噪声波浪下的运动以及两船间隙中点处的波面升高.对白噪声试验数据进行谱分析后,可得船体六自由度运动的RAO.用实际波面升高的RAO来调节自由面阻尼系数ε,从而抑制纯势流计算下剧烈的间隙水体共振.并采用此自由面阻尼计算两船运动RAO,与实测船体运动RAO对比,验证数值算法的可靠性.
3 数值与试验结果对比由于两船近靠时,间隙液面的黏性效应十分显著,首先采用阻尼盖的方法对间隙中的流场进行修正,再进行双船的计算和分析.通过模型试验选取合理的自由面阻尼ε,分析浪向的改变对水体共振的影响.基于阻尼盖修正的结果,验证在斜浪和迎浪条件下数值计算的可靠性,进而研究了135°~225°浪向下两船系统的运动特性,揭示斜浪下两船之间水动力干扰的规律.最后,分析了浪向的变化对两船平均漂移力的影响.
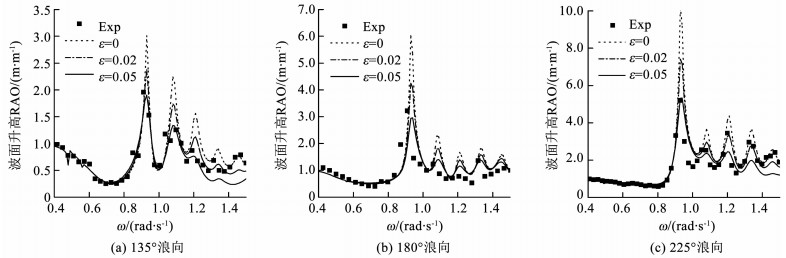
3.1 间隙水体共振由于之前的研究大多考虑迎浪下的多浮体问题而较少关注其他浪向,首先研究浪向的变化对阻尼盖添加的影响.图 4为不同浪向下间隙中点处的波面升高RAO,并考虑自由面阻尼为0, 0.02和0.05这3种情况,通过与试验值进行对比选取合适的自由面阻尼.观察图 4(a)、(b)、(c)发现,两船在3种不同浪向下,自由面阻尼的施加均有效降低了水体共振的峰值,而对其他非共振频率处的影响微弱.当自由面阻尼ε=0.05时,不同浪向下波面升高的计算值均能与试验值吻合.由此推断,浪向在迎浪左右45°范围内时,可选取相同的自由面阻尼进行计算.
|
图 4 不同浪向下间隙中点处波面升高RAO Figure 4 Free surface elevation RAO at the gap center point under different wave directions |
研究发现,数值模拟与试验的峰值频率虽十分接近但并不完全吻合(相差0.02),这一现象在Bunnik等[16]的研究中有所提及,即峰值频率的偏移是由在船体内液面加刚性盖来消除不规则频率导致的,可通过细分网格来消除.可见图中错峰现象并不明显,也间接验证了网格精度的可靠性.
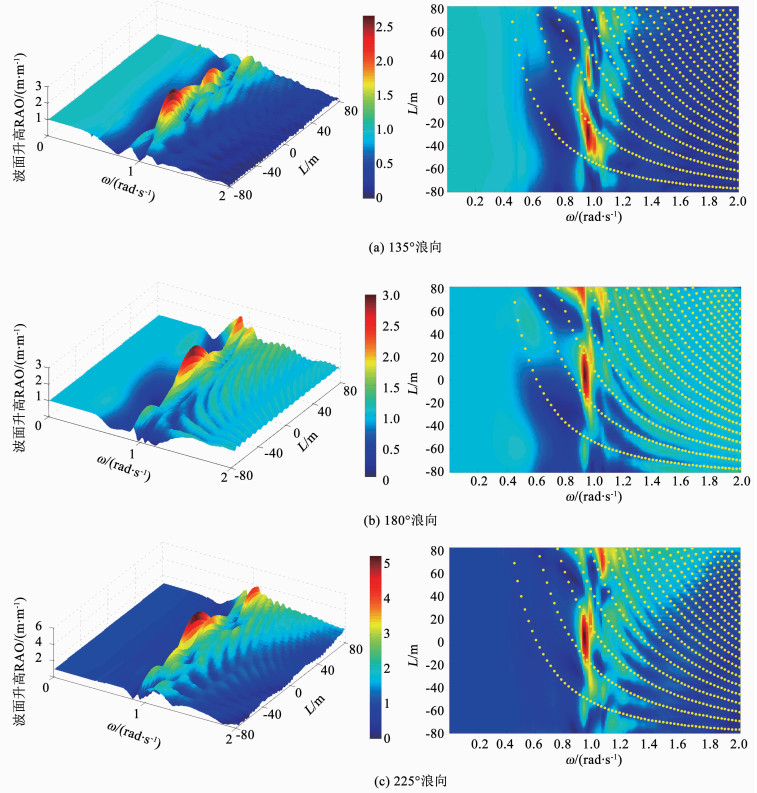
Molin等[17]指出两船的间隙可视为两端开口的月池模型,其两端流场的非连续性过度导致边界效应明显,因此,波浪在间隙内容易产生反射,并与入射波、绕射波和辐射波叠加形成复杂的共振现象.表 3列出试验测得的前四阶水体共振频率,可见除了高阶(3、4阶)固有频率由于试验精度存在微小差异,浪向的变化并不改变其固有频率.为了进一步研究浪向对间隙波面共振模态的影响,计算了不同浪向下,沿船长方向(-80 m<L<80 m)范围内间隙中点处波面升高的RAO,如图 5.可以看出,浪向的变化对低阶共振模态和幅值均有影响,而高阶共振模态则保持不变.下文首先讨论浪向对水体共振模态的影响.
| 表 3 试验测得间隙水体共振模态 Table 3 Modes of gap water resonance measured in tests |
|
图 5 不同浪向下间隙中线处波面升高RAO (L=0 m为LNGC船中处) Figure 5 Free surface elevation RAOs along the gap symmetry line under different wave directions (L=0 refers to the midship of LNGC) |
低阶共振模态是受入射波、绕射波、辐射波和反射波相叠加的联合影响.由图 5(b)、(c)可知,在180°和225°浪向下,波面升高的极大值发生在一阶模态,并位于船中位置.而在图 5(a) 135°浪向下,FLNG的遮蔽抑制了一阶模态的水体运动,此时二阶共振最为剧烈并导致峰值位置向船中的两侧偏移.
当频率ω>1.2 rad/s时,间隙内沿船长方向形成了稳定的高阶水体共振模态,此时高频波浪的强穿透性使得其不受浪向(入射势)的影响.同时高频波浪作用下船体运动较小,辐射势影响弱,因此高频共振模态与两船固定时情况相同,遵守由Bunnik等[16]提出的间隙波浪s反射模型.图 5中黄色点状线为半波长的整数倍与频率的函数曲线并满足线性色散关系(如式(6),其中λ为波长,g为重力加速度),将其沿y轴向负方向(船尾)移动半个LNGC船长覆盖至波浪RAO图上.可见每个共振频率下相邻峰值间距0.5 λ,在间隙中沿船长方向依次排列形成驻波.
| $ \frac{\mathit{n}}{2}\mathit{\lambda }{\rm{ = }}\frac{{{\rm{ \mathsf{ π} }}\mathit{g}}}{{{\mathit{\omega }^{\rm{2}}}}}\mathit{n}{\rm{, }}\;\mathit{n}{\rm{ = 1, 2, 3, }} \cdots {\rm{}} $ | (6) |
浪向对共振幅值的影响也十分显著.当浪向为225°时,波面共振最剧烈,最大峰值可达到入射波高的5倍多;当浪向为135°时,波面共振最弱,最大峰值仅为入射波高的2.7倍.由此可见,当浪向为135°时,FLNG迎浪并有效遮蔽来波,抑制了间隙内的波面运动;当浪向为225°时,LNGC迎浪,但由于其体积较小,无法有效遮蔽来波从而加剧间隙内的波面共振.这一现象在研究大间距的旁靠问题时也被Fang和Chen[10]发现,并指出自由漂浮时两船的摇荡增大了间隙水体运动的幅值.因此,从LNGC一侧入射的斜浪将引发间隙水体的剧烈共振,这在工程中十分不利.
3.2 双船运动数值计算的试验验证在选取适当的阻尼系数“epsilon”从而抑制水体共振的基础上,采用此系数来计算迎浪和斜浪下双船重心处的运动RAO,并与白噪声试验的谱分析结果进行对比,从而验证数值算法的准确性.由于两船间隙对横向运动的影响十分敏感,着重选取了横荡、横摇和首摇3个自由度进行分析,如图 6、7.

|
图 6 135°斜浪下两船横荡、横摇和首摇RAO计算值与试验值对比 Figure 6 Comparisons of calculated and test results for the sway, roll and yaw motion RAOs of two vessels under 135°oblique waves |

|
图 7 180°迎浪下两船横荡、横摇和首摇RAO计算值与试验值对比 Figure 7 Comparisons of calculated and test results for the sway, roll and yaw motion RAOs of two vessels under 180°head waves |
斜浪工况下,列举了135°浪向下的两船运动.观察图 6发现,对于横荡RAO曲线(尤其FLNG),其在两船横摇固有频率处均发生振荡,由此推断两船的横荡与横摇之间存在一定程度的耦合作用.而在迎浪情况下,由于横摇幅值较小,对横荡的耦合作用较小.对于横摇运动,数值模拟能够准确地捕捉两船的固有频率,而峰值较实际值偏小.这是由于线性黏性横摇阻尼低估了谐摇大幅运动时的实际阻尼值,导致计算值偏大.对于首摇运动,其受到高频水体共振的影响较为明显,尤其是质量较小的LNGC.由图 6可知,各自由度的数值和试验结果能够较好吻合,说明了数值方法的可靠性.当0.9 rad/s≤ω≤1.2 rad/s时,施加自由面阻尼ε=0.05能够较好地抑制无黏性时的较大运动,使得峰值降低并接近真实值.而对比图 4(a)发现,这正对应间隙水体发生共振的频率,因此,人工阻尼的施加不仅抑制自由面的大幅振荡,也有效抑制了浮体运动在水体共振频率处的振荡.
迎浪工况下,单船的横向波浪力较小,但是由于两船的不对称性和间隙的存在,同样引发了强烈的水动力干扰和横向运动,如图 7所示.然而,虽然迎浪下的数值结果符合基本趋势但幅值偏小,尤其是FLNG.这是由于试验中不可避免地存在首摇运动,加大了船体的横向波浪力,无法模拟数值计算中绝对的迎浪条件.对于运动相对较小的FLNG,这种系统误差将被放大.由于本文着重研究不同浪向,尤其是斜浪下双船旁靠的运动特性,对此并不做过多研究.
3.3 不同浪向下两船的运动由3.1和3.2可知,可以用相同的自由面阻尼ε对不同浪向下的波面和船体运动进行计算和分析.基于以上结论,本文采用阻尼因子0.05计算了135°~225°所有浪向下两船的横向运动,并分析浪向变化的影响.计算结果见图 8~10.
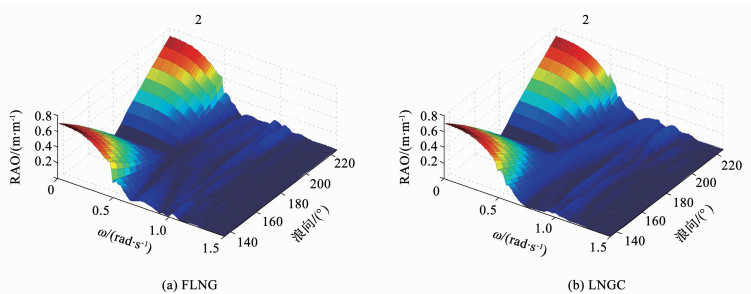
|
图 8 不同浪向下FLNG和LNGC的横荡RAO Figure 8 Sway RAOs of FLNG and LNGC under different wave directions |
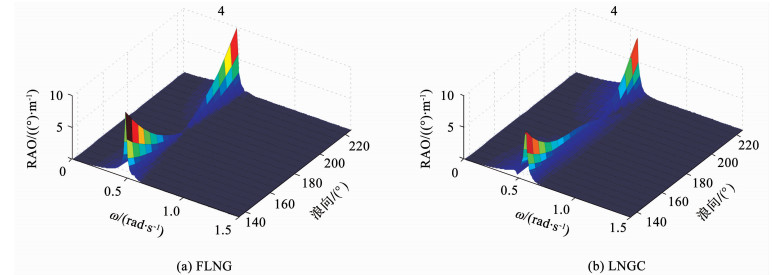
|
图 9 不同浪向下FLNG和LNGC的横摇RAO Figure 9 Roll RAOs of FLNG and LNGC under different wave directions |
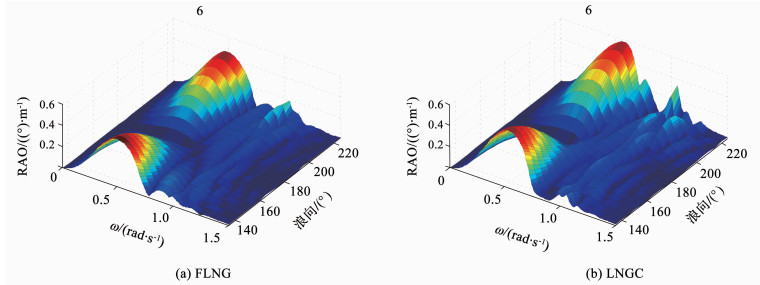
|
图 10 不同浪向下FLNG和LNGC的首摇RAO Figure 10 Yaw RAOs of FLNG and LNGC under different wave directions |
观察上述3个结果图发现,在低频区域两船运动RAO大致呈现对称的形式.值得注意的是,图 9(b)中LNGC的横摇RAO并非在180°浪向下,而在约195°浪向时达到最小值,这一非对称现象是由FLNG在斜浪下的水动力干扰导致.这一现象表明,当LNGC处于180°~225°迎浪一侧时,在某一特定浪向下的横摇反而得到了抑制.
图 11(a)、(b)对比了两船在135°与225°斜浪下运动RAO的极值,由于横荡所受浪向的影响十分微弱,仅对比横摇和首摇运动.首先对于FLNG,发现其对浪向的变化极不敏感;而对于LNGC,发现其在135°浪向下的运动峰值较小,相比225°浪向下横摇和首摇分别降低19.77%和6.89%.可见因为FLNG的体积较大,当其处于迎浪(135°浪)一侧时对LNGC的遮蔽效应较之LNGC在迎浪(225°浪)一侧时对FLNG的遮蔽效应更强,而LNGC对FLNG的遮蔽影响不明显.

|
图 11 两船横摇、首摇和高频首摇RAO在135°与225°浪向下运动RAO极值对比 Figure 11 Peak values of roll, yaw and high-frequency yaw RAO of two vessels under 135°and 225°wave directions |
对于激发水体共振的高频区域(0.9~1.2 rad/s),由图 8、10发现,横荡和首摇随着浪向趋近225°有所加剧,这一趋势与3.1节中间隙水体共振幅值随浪向的变化趋势相吻合.图 11(c)为两船在135°和225°斜浪下首摇高频(0.9~1.2 rad/s)运动RAO的极值,发现225°浪向下两船的高频运动十分剧烈,两船幅值可达到图 11(b)中对应极值的42%(FLNG)和58%(LNGC),此时水体共振引发的高频运动不容忽视.而当FLNG处于迎浪侧时(135°浪向),两船的高频运动峰值显著降低,相比225°浪向下分别降低了47.36%(FLNG)和61.76% (LNGC).综上,近靠时FLNG的遮蔽效应对两船高频运动的抑制效果十分显著.
3.4 不同浪向下两船的平均漂移力基于对波面升高和船体运动的计算分析,进一步探讨浪向对FLNG和LNGC平均漂移力的影响.由于浮体的平均漂移力是基于波面升高和船体运动响应而计算得到的,对二者的精确计算为获得可靠的平均漂移力提供了保障.Fournier等[18]证明了同一自由面阻尼对波面升高、船体运动和二阶力计算的准确性,因此,沿用前文得到的自由面阻尼ε=0.05,采用中场法对不同浪向下两船的二阶横荡漂移力进行计算,如图 12,其中虚线表示单船情况下的结果.

|
图 12 不同浪向下FLNG和LNGC的横荡平均漂移力RAO Figure 12 Sway mean drift force RAO of FLNG and LNGC under different wave directions |
首迎浪条件下,由图 12可知,两船在水体共振频率处受到向两侧外推的漂移力(FLNG负向LNGC正向).而斜浪下则截然不同:迎浪侧船体(135°浪FLNG或225°浪LNGC)的平均漂移力与单船情况下的十分相似,不同的是在水体共振频率处受到向外侧的漂移力;背浪侧船体(135°浪LNGC或225°浪FLNG)的平均漂移力则与迎浪情况相似.因此,对于斜浪工况,迎浪一侧的船体所受的二阶漂移力为入射波对单船的贡献叠加水体共振的影响,背浪侧船体被遮蔽从而主要受水体共振的影响.
值得注意的是,当浪向为225°时,剧烈的水体共振对二阶力贡献十分明显.例如图 12 (a)中,225°浪向下FLNG的负向漂移力最大可达到迎浪时的4倍左右.在图 12 (b)中,对于225°浪向下的LNGC,水体共振改变负向漂移力为正值,表明其抵消并超过入射波的贡献,使得漂移力的正峰值甚至超过135°和180°浪向下的.这对系泊系统和两船间连接系统的安全性提出挑战.
4 结论1) 对于阻尼盖法,当浪向在迎浪左右45°范围内时,可选取相同的自由面阻尼进行计算.浪向的变化对低阶水体共振的模态和幅值均有影响,而高阶共振模态则保持不变.
2) 通过数值和试验对比,发现迎浪下两船横向运动的计算值偏小,斜浪下两船的横摇与其他模态存在耦合作用.人工阻尼的施加有效抑制了船体在水体共振频率处的大幅振荡,并使得数值模拟与试验吻合.
3) 通过对比不同浪向下两船相互遮蔽时的运动,发现当FLNG在迎浪侧时,其对LNGC的遮蔽效应更强,并且FLNG遮蔽效应对两船高频运动的抑制效果十分显著.
4) 通过计算不同浪向下两船的平均漂移力,发现迎浪侧的船体主要受入射波的影响,背浪侧的船体被遮蔽从而主要受间隙水体共振影响.而在225°浪下,剧烈的水体共振对两船平均漂移力的贡献更为突出.
| [1] |
OHKUSU M. On the heaving motion of two circular cylinders on the surface of a fluid[J]. Reports of Research Institute for Applied Mechanics, 1969, 17(58): 167-185. DOI:10.1093/qjmam/2.2.218 |
| [2] |
VAN OORTMERSSEN G. Hydrodynamic interaction between two structures floating in waves[C]// Proceedings of the 2nd International Conference on Behavior of Offshore Structures (BOSS'79). London, UK: The Law and Practice of the International Court, 1979: 339-356.
|
| [3] |
CHOI Y R, HONG S Y. An analysis of hydrodynamic interaction of floating multi-body using higher-order boundary element method[C]// Proceedings of the 12th International Offshore and Polar Engineering Conference. Kitakyushu, Japan: International Society of Offshore and Polar Engineers, 2002: 303-308.
|
| [4] |
HONG S Y, KIM J H, CHO S K, et al. Numerical and experimental study on hydrodynamic interaction of side-by-side moored multiple vessels[J]. Ocean Engineering, 2005, 32(7): 783-801. DOI:10.1016/j.oceaneng.2004.10.003 |
| [5] |
XU X, LI X, YANG J M. Hydrodynamic interactions of three barges in close proximity in a floatover installation[J]. China Ocean Engineering, 2016, 30(3): 343-358. DOI:10.1007/s13344-016-0023-9 |
| [6] |
PESSOA J, FONSECA N, GUEDES SOARES C. Numerical study of the coupled motion responses in waves of side-by-side LNG floating systems[J]. Applied Ocean Research, 2015, 51: 350-366. DOI:10.1016/j.apor.2015.01.012 |
| [7] |
HUIJSMANS R, PINKSTER J A, DE WILDE J. Diffraction and radiation of waves around side-by-side moored vessels[C]// Proceedings of the 11th International Offshore and Polar Engineering Conference. Stavanger, Norway: International Society of Offshore and Polar Engineers, 2001: 406-412.
|
| [8] |
NEWMAN J N. Progress in wave load computations on offshore structures[C]// Proceedings of the 23rd International Conference Offshore Mechanics & Arctic Engineering. Vancouver, Canada: The American Society of Mechanical Engineers, 2004: 20-25.
|
| [9] |
CHEN X B. Offshore hydrodynamics and applications[J]. Ies Journal Part A Civil & Structural Engineering, 2011, 4(3): 124-142. DOI:10.1080/19373260.2011.595903 |
| [10] |
FANG M C, CHEN G R. The relative motion and wave elevation between two ships advancing in waves[J]. International Shipbuilding Progress, 2002, 49(3): 177-194. DOI:10.1016/s0029-8018(00)00042-1 |
| [11] |
KIM K, KIM Y, KIM M. Time-domain analysis of motion responses of adjacent multiple floating bodies in waves[C]// Proceedings of the 18th International Offshore and Polar Engineering Conference. Vancouver, Canada: International Society of Offshore and Polar Engineers, 2008: 301-307.
|
| [12] |
SHIVAJI G T, SEN D. Time domain simulation of side-by-side floating bodies using a 3D numerical wave tank approach[J]. Applied Ocean Research, 2016, 58: 189-217. DOI:10.1016/j.apor.2016.03.014 |
| [13] |
刘应中, 缪国平. 船舶在波浪上的运动理论[M]. 上海: 上海交通大学出版社, 1987. LIU Yinzhong, MIAO Guoping. Theory of ship motions in waves[M]. Shanghai: Shanghai Jiao Tong University Press, 1987. |
| [14] |
CHEN X B. Middle-field formulation for the computation of wave-drift loads[J]. Journal of Engineering Mathematics, 2007, 59(1): 61-82. DOI:10.1007/s10665-006-9074-x |
| [15] |
ZHAO W H, YANG J M, HU Z Q, et al. Experimental and numerical investigation of the roll motion behavior of a floating liquefied natural gas system[J]. Science China Physics, Mechanics and Astronomy, 2013, 56(3): 629-644. DOI:10.1007/s11433-012-4914-3 |
| [16] |
BUNNIK T, PAUW W, VOOGT A. Hydrodynamic analysis for side-by-side offloading[C]// Proceedings of the 19th International Offshore and Polar Engineering Conference. Osaka, Japan: International Society of Offshore and Polar Engineers, 2009: 648-653.
|
| [17] |
MOLIN B, REMY F, KIMMOUN O, et al. Experimental study of the wave propagation and decay in a channel through a rigid ice-sheet[J]. Applied Ocean Research, 2002, 24(5): 247-260. DOI:10.1016/S0141-1187(03)00005-1 |
| [18] |
FOURIER J R, NACIRI M, CHEN X B. Hydrodynamics of two side-by-side vessels experiments and numerical simulations[C]// Proceedings of the 16th International Offshore and Polar Engineering Conference. San Francisco, USA: International Society of Offshore and Polar Engineers, 2006: 158-165.
|
 2018, Vol. 50
2018, Vol. 50



