引用本文

王淼, 王锦, 张超. 优化填料布置及配水对冷却塔性能的影响[J]. 哈尔滨工业大学学报, 2018, 50(8): 124-131. DOI: 10.11918/j.issn.0367-6234.201803100.

WANG Miao, WANG Jin, ZHANG Chao. Effect of fill layout and water flow rate distribution on the performance for cooling tower[J]. Journal of Harbin Institute of Technology, 2018, 50(8): 124-131. DOI: 10.11918/j.issn.0367-6234.201803100.

基金项目

国华宁海电厂海水冷却塔新型填料和进风导流冷却效率分析研究(C15L00010)

作者简介

王淼(1988—)，女，博士研究生;
王锦(1973—)，女，教授，博士生导师

通信作者

王锦, 14115313@bjtu.edu.cn

文章历史

收稿日期: 2018-03-20

Abstract Full text Figures/Tables PDF

优化填料布置及配水对冷却塔性能的影响

王淼¹, 王锦¹, 张超²

1. 北京交通大学土木建筑工程学院，北京 100044;
2. 国华宁海电厂电力与水利部门，浙江宁波 315000

收稿日期: 2018-03-20

基金项目: 国华宁海电厂海水冷却塔新型填料和进风导流冷却效率分析研究(C15L00010)

作者简介: 王淼(1988—)，女，博士研究生;
王锦(1973—)，女，教授，博士生导师

通信作者: 王锦, 14115313@bjtu.edu.cn

摘要: 为明确填料布置及配水对冷却塔冷却性能的影响，以浙江国华宁海电厂二期工程6#冷却塔为原型，建立三维数值模型，通过自定义函数加载质量、动量和能量计算程序，与实测对比，模拟结果准确.对比分析3种填料和5种填料布置对超大型冷却塔冷却性能的影响，发现与双向波和双斜波相比，S波冷却效率最优.与S波1.5 m填料等高布置相比，沿径向按无量纲半径$ \check{r}$≤0.39 (内区)、0.39＜$ \check{r}$≤0.70 (中区)和0.70＜$ \check{r}$≤ 1 (外区)非等高1.25-1.5-1.25 m布置的出水温度降低了0.66 K，表明降低填料内区和外区高度，使得空气流速增加，空气流场分布更均匀.另外，当布水总量恒定时，增加冷却水含盐量，3种填料的出水温度均升高2 K左右，说明出水温度升高主要与海水自身性质有关，且受填料波型的影响较小.

关键词: 超大型冷却塔三维数值模拟填料非均匀布置非均匀配水冷却性能

Effect of fill layout and water flow rate distribution on the performance for cooling tower

WANG Miao¹, WANG Jin¹, ZHANG Chao²

1. School of Civil Engineering, Beijing Jiaotong University, Beijing 100044, China;
2. Department of Power Engineering and Water Conservancy, GuoHua Ninghai Power Plant, Ningbo 315000, Zhejiang, China

Abstract: In order to identify the effect of fill layout and water flow rate distribution on the cooling performance of cooling tower, a three-dimensional numerical model was established based on prototype of No.6 Cooling Tower in the Second Phase of Guohua Ninghai Power Plant in Zhejiang Province. Loading the mass, momentum, energy equation was computed by using user defined function. The comparision with the field measurement data proves the accuracy of the numerical calculation result. The effects of three kinds of fills and five kinds of fills layouts on cooling performance of super-large cooling tower weve compared and analyzed. It is found that compared with biphasic wave and double oblique wave, the cooling efficiency of S wave is optimal. For S wave, based on the dimensionless radius $ \check{r}$≤0.39 (inner zone), 0.39 < $ \check{r}$≤0.70 (middle zone) and 0.70 < $ \check{r}$≤1 (outer zone), the outlet water temperature of non-uniform layout 1.25-1.5-1.25 m is 0.66 K lower than the outlet water temperature of the uniform fill layout pattern 1.5 m. It is shown that the decreased fill height in inner and outer zones results in a higher air velocity and more uniform distribution of air velocity. In addition, increasing the salinity of cooling water made the outlet water temperature of three kinds of fills improve by about 2 K. It is indicated that the rise of outlet water temperature is related to the nature of seawater itself, and fill types has little impact on outlet water temperature.

Key words: super-large cooling tower three dimensional numerical simulation fill non-uniform layout non-uniform water flow rate distribution cooling performance

随着核电站规模的不断扩大，普通冷却塔作为冷源设备已不能满足大型核电站循环水冷却的需求，因此，超大型冷却塔应运而生.通常将淋水面积大于12 000 m²，塔高超过《工业循环水冷却设计规范》(GB/T 50102—2014) 165 m限制的冷却塔称为超大型冷却塔^[1]，其主要传热传质区为喷淋区、填料区和雨区.由于填料区占冷却塔总散热量的60%~ 70%^[2]，同时，喷淋区配水优劣直接影响填料区两相流的传热传质，因此，合理优化超大型冷却塔的填料布置和配水形式，对提高超大型冷却塔的冷却性能具有重要的意义.然而，试验方法很难模拟实际工程中空气与液滴复杂的传热传质过程，为此，需要对超大型冷却塔内空气流场特性进行数值模拟分析.

目前，国内外对冷却塔传热传质模型计算常采用Merkel方法^[3]或Poppe方法^[4]，如国外学者Kloppers等^[5]针对3种不同填料类型，采用Merkel和Poppe模型进行冷却塔冷却性能计算对比分析，研究发现，Poppe模型计算的出水温度精度较高.国内赵元斌等^[6]采用Merkel模型，计算分析了填料非均匀布置对冷却塔冷却性能的影响，得出与均匀布置相比，填料非均匀布置的出水温度降低约0.2 K.黄东涛等^[7]采用数值分析的方法研究了填料区非均匀布置及喷淋区非均匀配水对冷却塔性能的影响，发现填料非均匀布置及非均匀配水的出水温度比填料等高均匀配水的出水温度低0.7 K，比填料等高非均匀配水的出水温度低0.3 K.金台等^[8]发现冷却塔采用分区配水后出水温度可降低约0.55 K.赵顺安等^[9]通过优化冷却塔配水设计，提高了冷却塔配水均匀性，使冷却塔冷却性能增加.郑水华等^[10]指出优化填料高度和配水均可使出水温度降低0.2 K.国际上Williamson^[11-12]、Kroger^[13]和Kloppers^[14]采用Popper模型对冷却塔进行了二维数值模拟，并对填料高度进行了优化，得出填料高度增加，出水温度下降的结论.Alkhedhair等^[15-16]模拟了管道喷淋时喷嘴对空气流场的影响，得出减小喷嘴直径，促进了空气与液滴间蒸发，可提高冷却塔的冷却性能的结论.总体来看，文献[6-16]讨论了填料布置或配水对冷却塔冷却性能的影响，但文献[6-10]假设刘易斯数(热扩散系数与质量扩散系数的比值)等于1，并忽略了冷凝水蒸发损失引起的热量变化.文献[12-15]采用了二维数值模型分析塔内不同区域的冷却性能，但对z向截面空气流场分布特征的研究具有一定局限性.

为此，以浙江国华宁海电厂二期工程淋水面积13 000 m²的超大型冷却塔为原型，建立超大型冷却塔三维数值模型.利用Popper理论和FLUENT软件，考虑蒸发损失引起的水量变化，采用自定义函数判断冷却塔出口空气为未饱和或过饱和状态，并对超大型冷却塔进行数值模拟计算.开展不同填料类型、不同填料高度布置、不同区域淋水密度和不同海水盐度对冷却塔冷却性能的影响研究，分析冷却塔内空气流场和传热特性，全面优化冷却塔填料和配水布置，揭示冷却水含盐量对冷却塔冷却性能影响规律.

1 计算模型 1.1 几何模型和数学模型

浙江国华宁海电厂中超大型自然通风湿式冷却塔的几何参数如图 1所示.本文采用分离隐式求解器、SIMPLE算法^{[12-13, 17]}对空气流场进行求解，并采用雷诺平均Navier-Stokes方程描述计算域内空气运动，用标准k-ε湍流模型进行湍流封闭.编写自定义函数分别加载到喷淋区、填料区和雨区，对塔内两相流间的质量、动量和能量传递进行数值模拟计算.空气与液滴传热传质的详细数学模型可参见文献[18-23].

图 1 冷却塔的几何参数、计算域及边界条件 Figure 1 Geometrical parameters of cooling tower, computing domain and boundary conditions

空气通用控制方程为

$ \mathit{\Delta }{\rm }\!\!\cdot\!\!{\rm }\left( \mathit{\rho \mu \varphi }{\rm -}{{\mathit{\Gamma }}_{\mathit{\varphi }}}{{\mathit{\Delta }}_{\mathit{\varphi }}} \right){\rm =}{{\mathit{S}}_{\mathit{\varphi }}}{\rm .} $

(1)

式中：φ为标量(指代速度、温度、湍动能或湍流动能耗散率等)，ρμφ为对流项；Г_φΔ_φ为扩散项；Г_φ为标量的扩散项系数；S_φ为源项.

液滴能量传递方程为

$ {{\mathit{m}}_{{\rm p}}}{{\mathit{c}}_{{\rm p}}}\frac{{\rm d}{{\mathit{T}}_{{\rm p}}}}{{\rm d}\mathit{t}}{\rm =}\mathit{h}{{\mathit{A}}_{{\rm p}}}\left( {{\mathit{T}}_{{\rm ab}}}{\rm -}{{\mathit{T}}_{{\rm p}}} \right){\rm +}\frac{{\rm d}{{\mathit{m}}_{{\rm p}}}}{{\rm d}\mathit{t}}{{\mathit{h}}_{{\rm fg}}}{\rm .} $

(2)

式中：m_p为液滴质量流率，kg/(m²·s)；c_p为比热容，J/(kg·K)；T_p为液滴的温度，K；A_p为水滴表面积，m²；T_ab为空气的温度，K；h_fg为汽化潜热，J/kg；h为传热系数，W/(m² ·K).

当水蒸气为不饱和且无冷凝水析出时，能量方程源项可表示为

$ {{\mathit{S}}_{{\rm vap}}}{\rm =}\frac{{{\mathit{m}}_{{\rm evap}}}}{{{\mathit{L}}_{\mathit{fi}}}}{\rm , } $

(3)

$ {{\mathit{S}}_{{\rm con}}}{\rm =0, } $

(4)

$ {\mathit{S}_{\rm{q}}}{\rm{ = }}\frac{{{\mathit{m}_{{\rm{w1}}}}{\rm{\cdot}}{\mathit{c}_{{\rm{pw}}}}{\rm{\cdot}}\mathit{\Delta }{\mathit{T}_{{\rm{wn}}}}{\rm{ + }}{\mathit{m}_{{\rm{evap}}}}\left( {\frac{{{\mathit{T}_{{\rm{w1}}}}{\rm{ + }}{\mathit{T}_{{\rm{w0}}}}}}{2}{\rm{ - 298}}{\rm{.15}}} \right){\rm{\cdot}}{\mathit{c}_{{\rm{pv}}}}{\rm{ - }}{\mathit{h}_{{\rm{fg}}}}}}{{{\mathit{L}_{{\rm fi}}}}}{\rm{ + }}{\mathit{S}_{{\rm{con}}}}{\rm{\cdot}}{\mathit{h}_{{\rm{fg}}}}{\rm{.}} $

(5)

当水蒸气过饱和且有冷凝水析出时，存在：

$ {\mathit{S}_{{\rm{vap}}}}{\rm{ = }}{\mathit{\omega }_{{\rm{sat, Ta}}}}{\rm{ - }}\mathit{\omega }{\rm{, }} $

(6)

$ {\mathit{S}_{{\rm{con}}}}{\rm{ = }}{\mathit{m}_{{\rm{evap}}}}{\rm{ - }}{\mathit{S}_{{\rm{vap}}}}{\rm{.}} $

(7)

式中：S_q为能量源项；m_w1为填料底部水的质量流率，kg/(m²·s)；c_pw为水滴定压比热容，J/(kg·K)；ΔT_wn为填料区水温差，K；m_evap为水蒸发量；T_w1与T_w0分别为填料底部与顶部水温，K；c_pv为水蒸气定压比热容，J/(kg·K)；L_fi为填料高度，m；ω_{sat, Ta}为空气温度下对应的饱和含湿量；ω为含湿量; S_vap为水蒸气源项; S_con为冷凝水源项.

填料的热力和阻力计算公式均源自填料性能测试标准^[24].可得不同填料类型及高度的热力性能如表 1^[25]所示，其中λ为空气质量流量与水质量流量的比值.此外，填料区阻力计算可表示为

$ {\rm{\Delta }}\mathit{p}{\rm{ = }}{\mathit{A}_\mathit{\beta }}{\rm{\cdot}}{\mathit{v}^\mathit{m}}{\rm{\cdot}}\mathit{\gamma }{\rm{.}} $

(8)

表 1 填料在不同波型与高度下的热力性能 Table 1 Thermal properties of the fill under different height and wave types

式中：γ为空气比重，kg/(m²·s²)；v为填料区平均风速，m/s；A_β和m为填料系数(不同填料类型和高度的A_β和m见表 2^[25]).

表 2 不同波型与高度下填料系数 Table 2 Fill coefficient under different height and wave types

采用FLUENT中面源射流方式对喷淋区的液滴进行布水，设置液滴直径为0.005 m^[26].液滴在运动中受阻力、浮力和重力作用.因此，可以得到笛卡尔坐标系下Z方向液滴平衡方程：

$ \frac{{{\rm{d}}{\mathit{u}_{{\rm{pz}}}}}}{{{\rm{d}}\left( {{\rm{ - }}\mathit{z}} \right)}}{\rm{ = }}\frac{{\left( {{\mathit{\rho }_{\rm{p}}}{\rm{ - }}\mathit{\rho }} \right)\mathit{g}}}{{{\mathit{\rho }_{\rm{p}}}{\mathit{u}_{{\rm{pz}}}}}}{\rm{ - }}\frac{{{\mathit{f}_{\rm{z}}}}}{{{\mathit{m}_{\rm{p}}}{\mathit{u}_{{\rm{pz}}}}}}{\rm{, }} $

(9)

$ {\mathit{f}_{\rm{z}}}{\rm{ = }}{\mathit{C}_{\rm{p}}}\mathit{R}{\mathit{e}_{\rm{p}}}\frac{{{\rm{ \mathsf{ π} }}{\mathit{d}_{\rm{p}}}\mathit{u}}}{8}\left( {{\mathit{u}_{{\rm{pz}}}}{\rm{ + }}{\mathit{u}_{\rm{a}}}} \right){\rm{, }} $

(10)

$ \mathit{R}{\mathit{e}_{\rm{p}}}{\rm{ = }}\frac{{\mathit{\rho }{\mathit{d}_{\rm{p}}}\sqrt {\mathit{u}_{{\rm{pz}}}^2{\rm{ + }}\mathit{u}_{\rm{a}}^2} }}{\mathit{u}}{\rm{, }} $

(11)

$ {\mathit{C}_{\rm{p}}}{\rm{ = }}\frac{{{\rm{24}}}}{{\mathit{R}{\mathit{e}_{\rm{p}}}}}{\rm{ + }}\frac{{\rm{6}}}{{{\rm{1 + }}\sqrt {\mathit{R}{\mathit{e}_{\rm{p}}}} }}{\rm{ + 0}}{\rm{.4}}{\rm{.}} $

(12)

式中：f_z为液滴所受阻力，N；u_pz和u_a分别为液滴垂直向下的速度、空气垂直向上的速度，m/s；d_p为液滴直径；ρ_p和ρ分别液滴密度和空气密度，kg/m³；g为重力加速度，m/s²；u为液滴的动力黏滞系数，Pa·s；C_p为液滴阻力系数；Re_p为空气相对液滴运动的雷诺数.

1.2 网格划分及计算边界

建立直径800 m、高600 m圆柱体计算域，如图 1所示.计算域的直径是塔底直径的5.3倍，计算域的高是塔高的3.4倍.由于冷却塔几何结构规整、对称，采用结构化六面体网格对喷淋区、填料区和雨区的网格进行加密细化，其他区域的网格粗化.

在环境侧风条件下，设置圆柱体计算域迎风侧的边界条件为速度入口，速度方向与当地主导风向相同.圆柱体计算域背风侧和顶部的边界条件为压力出口.当数值计算满足能量残差在10^-6量级、其他各变量残差在10^-4量级、且迭代50步内出水温度变化小于0.01 ℃时，判断此时计算结果收敛.

为了讨论填料布置对冷却塔冷却性能的影响，沿径向将填料划分为不同区域.按无量纲半径$ \check{r}$将填料分为内、中、外3个区：$ \check{r}$≤0.39(内区)、0.39＜$ \check{r}$≤ 0.70(中区)、0.70＜$ \check{r}$≤1(外区)，及内、外两个区：$ \check{r}$≤0.5(内区)、0.5＜$ \check{r}$≤1(外区)两区，两种布置形式如图 2所示.沿轴向对填料高度进行非均匀布置，以填料高度1.5 m等高布置为基础，设计了4种填料非均匀布置方案，如图 3所示.填料非均匀1-1.5-1.5 m布置：在$ \check{r}$≤0.39(内区)内填料高度布置为1 m，0.39＜$ \check{r}$≤0.70(中区)、0.70＜$ \check{r}$≤1(外区)内填料高度均为1.5 m；填料非均匀1-1.25-1.5 m布置：在$ \check{r}$≤0.39(内区)内填料高度布置为1 m，0.39＜$ \check{r}$≤0.70(中区)内填料高度布置为1.25 m，0.70＜$ \check{r}$≤1(外区)内填料高度均为1.5 m；填料非均匀1.25-1.5-1.25 m布置：在$ \check{r}$≤0.39(内区)、0.70＜$ \check{r}$≤1(外区)内填料高度均为1.25 m，0.39＜$ \check{r}$≤0.70(中区)内填料高度布置为1.5 m；填料非均匀1.25-1.5 m布置：在$ \check{r}$≤0.5(内区)内填料高度布置为1.25 m，0.5＜$ \check{r}$≤1(外区)内填料高度均为1.5 m.

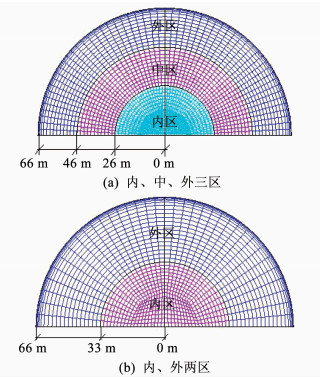
图 2 填料不同区域划分及网格分布 Figure 2 Different fill zone and grid distribution

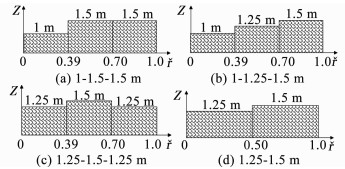
图 3 填料高度非均匀布置 Figure 3 Non-uniform layout of fill height

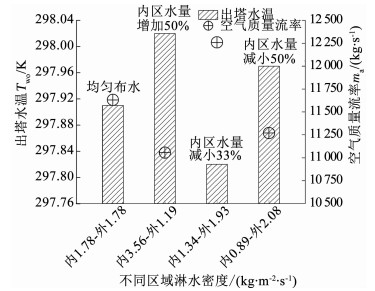
同时讨论了总水量恒定时，喷淋区非均匀布水(均匀布水1.78 kg/(m²·s)；内区水量增加50 %：内区3.56-外区1.19 kg/(m²·s)；内区水量减少33 %：内区1.34-外区1.93 kg/(m²·s)；内区水量减少50 %：内区0.89-外区2.08 kg/(m²·s))对冷却性能的影响.另外，研究了冷却水含盐量(淡水、含盐量为35 g/kg的海水、浓缩1倍的海水、浓缩1.5倍的海水和浓缩2倍的海水)对冷却塔冷却性能的影响，所有设计方案详见表 3.

表 3 填料布置和配水形式 Table 3 Non-uniform layout of fill height and water flow rate distribution

布置形式	半径范围(填料高度)/m			填料体积/ m³	水量分布/ (kg·m^-2·s^-1)		冷却水盐度
布置形式	内区	中区	外区	填料体积/ m³	内区	外区	冷却水盐度
1.5-1.5-1.5 m	$ \check{r}$≤0.39 (1.5 m)	0.39＜$ \check{r}$≤0.70 (1.5 m)	0.70＜$ \check{r}$≤1 (1.5 m)	10 258	1.78	1.78	淡水
1-1.5-1.5 m	$ \check{r}$≤0.39 (1 m)	0.39＜$ \check{r}$≤0.70 (1.5 m)	0.70＜$ \check{r}$≤1 (1.5 m)	9 727	1.78	1.78	淡水
1-1.25-1.5 m	$ \check{r}$≤0.39 (1 m)	0.39＜$ \check{r}$≤0.70 (1.5 m)	0.70＜$ \check{r}$≤1 (1.5 m)	9 162	1.78	1.78	淡水
1.25-1.5-1.25 m	$ \check{r}$≤0.39 (1.25 m)	0.39＜$ \check{r}$≤0.70 (1.5 m)	0.70＜$ \check{r}$≤1 (1.25 m)	9 114	1.78	1.78	淡水
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	1.78	1.78	海水
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	3.56	1.19	淡水
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	1.34	1.93	淡水
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	0.89	2.08	淡水
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	1.78	1.78	海水
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	1.78	1.78	海水浓缩1倍
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	1.78	1.78	海水浓缩1.5倍
1.25-1.5 m	$ \check{r}$≤0.5 (1.25 m)	—	0.5＜$ \check{r}$≤1 (1.5 m)	9 829	1.78	1.78	海水浓缩2倍

表 3 填料布置和配水形式 Table 3 Non-uniform layout of fill height and water flow rate distribution

1.3 网格独立性及有效性验证

采用表 4中工况1的环境参数对网格进行无关性检验，建立3套网格数分别为42万、69万和107万的结构化六面体模型，计算得到3套模型的出水温度分别为297.97，297.91和297.89 K.发现与网格数42万模型相比，网格数69万模型的出水温度降低了0.06 K.与网格数107万网格模型相比，网格数69万网格模型的出水温度增加了0.02 K.说明当网格数大于67万时，出水温度随网格数增加降低幅度缓慢.综合考虑，选用69万的网格模型.

表 4 冷却塔的模型验证 Table 4 Model validation through field test data of the cooling tower

2013年5月11日—5月15日，中国水科院根据《工业冷却塔测试规程》(DL/T 1027—2006)对宁海电厂冷却塔的出口水温进行现场实测.其后，选取了不同环境参数下两个工况的实测数据与模拟结果进行对比.得到两个实测工况出水温度与模拟出水温度的计算误差分别为0.18和0.28 K，相对误差分别为1.47 %和2.72 %，模型误差均未超过5%(见表 4).说明该模型具有足够的准确性和可靠性，可用于冷却塔性能优化研究.

2 计算结果分析 2.1 填料类型及布置对冷却塔冷却性能的影响

S波、双向波和双斜波的出水温度、空气质量流率、冷却效率和填料区压力降随填料布置的变化规律如图 4所示.从图 4 (a)可知，3种填料在相同布置形式时，S波出水温度均最低，双斜波出水温度居中，双向波出水温度最高.同时，由图 4 (b)可知，与双向波和双谐波相比，S波冷却效率和填料区压降均最高.说明S波冷却性能最优，这是由于该波弯曲次数较多，使得塔内液滴与空气换热更充分.此外，3种填料在不同布置形式时，非均匀1.25-1.5-1.25 m布置的出水温度均最低.例如，对S波而言，与1.5 m等高布置和非均匀布置(1-1.5-1.5 m，1-1.25-1.5 m和1.25-1.5 m)相比，非均匀1.25-1.5-1.25 m布置的出水温度分别降低了0.66，0.68，0.73和0.54 K.

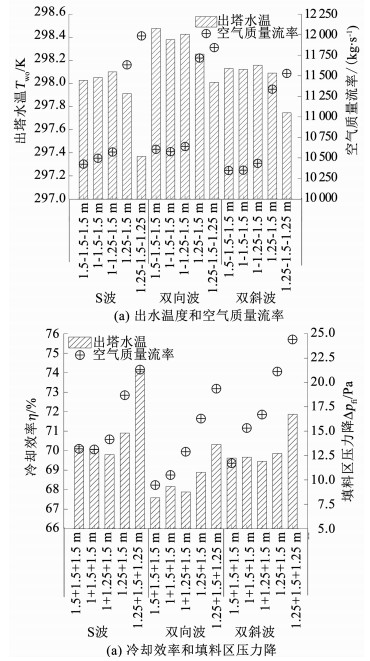
图 4 不同参数受填料类型和高度布置影响的变化 Figure 4 Effect of fill types and fill heights layout on different parameters

这主要由于非均匀1.25-1.5-1.25 m布置的空气质量流率最高，使塔内空气与液滴传热传质能力增强.例如，与S波的其他布置形式相比，非均匀1.25-1.5-1.25 m布置的空气质量流率平均增加了1 203 kg/s.此外，从经济性角度看，非均匀1.25-1.5-1.25 m布置的填料用量相比1.5 m等高布置减少了11.2 %，如表 3所示.说明合理优化冷却塔填料高度，能大大提高冷却塔冷却性能，同时能节约填料降低成本.

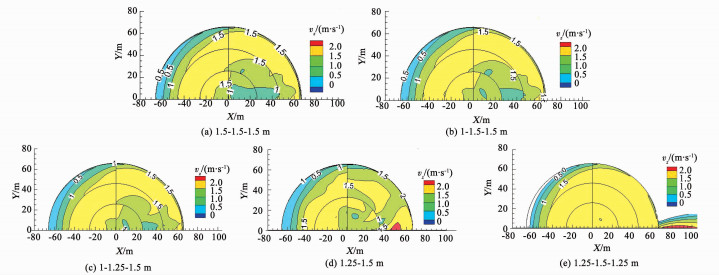
图 5、6所示为S波在不同填料布置形式时空气温度云图(Y=0)和速度云图(Z=14.48 m).由图 5可知，S波在5种填料布置情况下空气温度云图的变化趋势基本一致，即：塔心处空气温度最高，沿着塔壁方向空气温度逐渐降低，这是由于空气从塔壁进入后，越靠近塔心阻力越大，空气流速越小，内区两相流的传热传质能力越弱.因此，以1.5 m等高布置为基础，降低其内区填料高度，可使内区空气温度流场有所改善，换热能力增强.其次，相比其他非均匀布置，非均匀1.25-1.5-1.25 m布置的空气温度场和速度场分布更均匀.说明降低外区填料高度后，内区空气温度降低，且内区和中区空气流速也得到提高，大大促进了两相流传热传质能力.

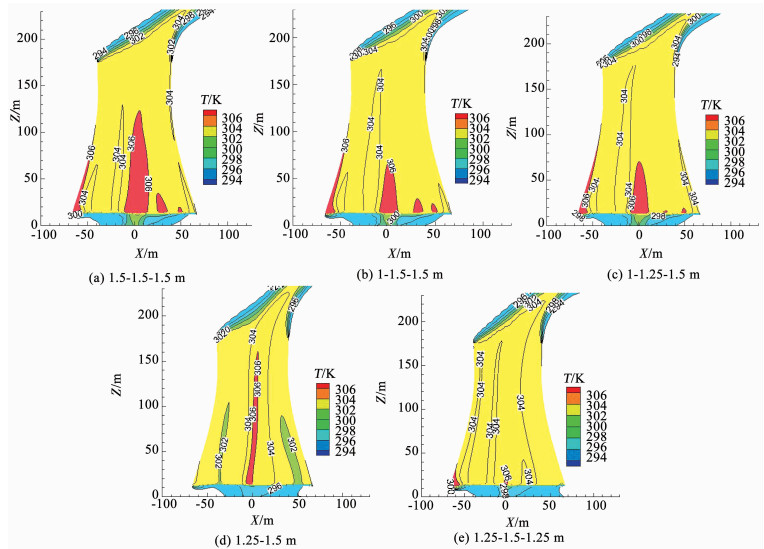
图 5 Y=0 m空气温度云图 Figure 5 Contours of air temperature at Y=0 m

图 6 Z=14.48 m填料顶面空气速度云图 Figure 6 Contours of air velocity at the top of the fill zone at Z=14.48 m

2.2 淋水密度对冷却塔冷却性能的影响

在布水总量恒定情况下，改变喷淋顶面内、外区淋水密度对出水温度和空气质量流量的影响如图 7所示.与均匀布水(内区1.78 kg/(m²·s)-外区1.78 kg/(m²·s))和非均匀布水(内区3.56 kg/(m²·s)-外区1.19 kg/(m²· s))相比，非均匀(内区1.34 kg/(m²·s)-外区1.93 kg/(m²·s))布水的出水温度分别下降了0.09和0.21 K，空气质量流率分别增加了627，1 203 kg/s.说明内区水量增加，阻力增大，空气质量流率减小，弱化了内区的传热传质能力.另外，与内区相比，外区仍有继续冷却液滴的能力，因此，适当增加外区水量可使其换热能力得到充分发挥，但过度增加外区水量，也不利于两相流的传热传质.例如，与非均匀(内区1.34 kg/(m²·s)-外区1.93 kg/(m²·s))布水相比，非均匀(区0.89 kg/(m²·s)-外区2.08 kg/(m²·s))布水的出水温度升高了0.16 K，空气质量流率下降了989 kg/s.因此，合理布水，才能有效地提高冷却效率.

图 7 淋水密度对冷却塔出水温度和空气质量流量的影响 Figure 7 Effect of water distribution intensity on outlet water temperature and air mass flow rate for cooling tower

2.3 海水浓度对冷却塔冷却性能的影响

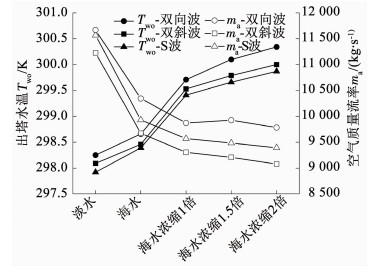
图 8为S波、双向波和双谐波的出水温度和空气质量流率受冷却水含盐量影响的变化.由图 8可知，冷却水从淡水到浓缩2倍海水，3种填料的出水温度均升高2 K左右，空气质量流率均下降约1 775 kg/s，说明出水温度升高受填料波型的影响较小，主要与海水自身性质有关.冷却水含盐量和空气流速是影响蒸发的主要原因之一.由于海水中含有大量盐、钙和镁离子等，增加冷却水含盐量后，离子浓度升高，海水的热力学性质被改变，水分子蒸发受到了阻碍，空气质量流率下降，最终导致空气与液滴间蒸发换热下降.因此，冷却水含盐量增加不利于空气与液滴间传热传质.Alshammiri^[27]研究了水体盐度对蒸发率的影响，得出水体盐度降低、空气流速增加、蒸发速率大大提高的结论.

图 8 海水浓度对冷却塔出水温度和空气质量流率的影响 Figure 8 Effect of seawater concentration on outlet water temperature and air mass flow rate for cooling tower

3 结论

1) S波冷却效率优于双向波和双斜波.对比S波5种填料布置的空气温度场，得到5种填料布置在塔心处空气温度均最高，沿塔壁方向空气温度逐渐降低的结论，但非均匀1.25-1.5-1.25 m布置的空气温度场分布最均匀.与1.5 m等高布置相比，非均匀1.25-1.5-1.25 m布置的出水温度降低了0.66 K，空气质量流率增加1 559 kg/s.因此，综合表明降低填料内、外区高度，可有效改善两相流的传热传质能力.

2) 与均匀(内区1.78 kg/(m²·s)-外区1.78 kg/(m²·s))布水相比，非均匀(内区1.34 kg/(m²·s)-外区1.93 kg/(m²·s))布水的出水温度下降0.99 K，空气质量流率增加627 kg/s.说明合理增加外区水量，可使外区换热能力得到充分发挥.

3) 海水浓缩倍数增加，则冷却塔冷却性能下降.这是由于海水含盐量增加，阻碍了水分子蒸发，减小了空气与液滴间换热量.

参考文献

[1]	中国人民共和国电力行业标准委员会. 工业循环水冷却设计规范: GB/T 50102—2014[S]. 北京: 中国计划出版社, 2014.
[2]	WILLIAMSON N, BEHNIA M, ARMFIELD S. Comparison of a 2D axisymmetric CFD model of natural draft wet cooing tower and a 1D model[J]. International Journal of Heat and Mass Transfer, 2008, 51(9/10): 2227.
[3]	MERKEL F. Verdunstungskühlung[M]. Berlin: Association of German Engineers, 1925: 123.
[4]	POPPE M, ROGENER H. Berechnung vonruckkuhlwerken[M]. Berlin: Association of German Engineers, 1991: 1.
[5]	KLOPPERS J, KROGER D. Loss coefficient correlation for wet cooling tower fills[J]. Applied Thermal Engineering, 2003, 23(17): 2201. DOI:10.1016/S1359-4311(03)00201-1
[6]	赵元斌, 杨志, 高明, 等. 填料非均匀布置对大型冷却塔冷却性能的影响[J]. 中国电机工程学报, 2013, 20(33): 96. ZHAO Yuanbin, YANG Zhi, GAO Ming, et al. Impact of fill non-uniform layout on cooling performance of large-scale cooling towers[J]. Proceedings of the Chinese Society for Electrical Engineering, 2013, 20(33): 96. DOI:10.13334/j.0258-8013.pcsee.2013.20.016
[7]	黄东涛, 杜成琪. 逆流式冷却塔填料及淋水分布的数值优化设计[J]. 应用力学学报, 2000, 17(1): 102. HUANG Dondtao, DU Chengqi. Numerical optimization on arrangement of the filling material and spraying water in cooling tower[J]. Chinese Journal of Applied Mechanics, 2000, 17(1): 102.
[8]	金台, 张力, 唐磊, 等. 自然通风湿式冷却塔配水优化的三维数值研究[J]. 中国电机工程学报, 2012, 32(2): 9. JIN Tai, ZHANG Li, TANG Lei, et al. Three-dimensional numerical study on water-distribution optimization in a natural draft wet cooling tower[J]. Proceedings of the Chinese Society for Electrical Engineering, 2012, 32(2): 9. DOI:10.13334/j.0258-8013.pcsee.2012.02.018
[9]	赵顺安, 冯春平, 顾建华, 等. 超大型自然通风逆流式冷却塔的配水设计[J]. 电力建设, 2009, 1(30): 53. ZHAO Shunan, FENG Chunping, GU Jianhua, et al. Water distribution design for large natural draft counter flow cooling tower[J]. Electric Power Construction, 2009, 1(30): 53.
[10]	郑水华, 金台, 罗坤, 等. 逆流式自然通风冷却塔热力性能的三维数值模拟[J]. 中南大学学报(自然科学版), 2013, 9(44): 3898. ZHENG Shuihua, JIN Tai, LUO Kun, et al. Three-dimensional numerical simulation on thermal performance in counter flow natural draft cooling tower[J]. Journal of Central South University (Science and Technology), 2013, 9(44): 3898.
[11]	WILLIAMSON N. Numerical modelling of heat and mass transfer and optimization of a natural draft wet cooling tower[D]. Sydney: University of Sydney, 2008.
[12]	WILLIAMSON N, ARMFIELD S, BEHNIA M. Numerical simulation of flow in a natural draft wet cooling tower-the effect of radial thermos fluid fields[J]. Applied Thermal Engineering, 2008, 28(2/3): 178.
[13]	KROGER D. Air-cooled heat exchangers and cooling towers[M]. Tulsa: Penn Well Corp, 2004: 50.
[14]	KLOPPERS J. A critical evaluation and refinement of the performance of wet-cooling towers[D]. Stellenbosch: University of Stellenbosch, 2003.
[15]	ALKHEDHAIR A, GURGENCI H, JAHN I, et al. Numerical simulation of water spray for pre-cooling of inlet air in natural draft dry cooling towers[J]. Applied Thermal Engineering, 2013, 61: 416. DOI:10.1016/j.applthermaleng.2013.08.012
[16]	ALKHEDHAIR A, JAHN I, GURGENCI H, et al. Numerical simulation of water spray in natural draft dry cooling towers with a new nozzle representation approach[J]. Applied Thermal Engineering, 2016, 98: 924. DOI:10.1016/j.applthermaleng.2015.10.118
[17]	ALWAKED R, BEHNIA M. Enhancing performance of wet cooling tower[J]. Energy Conversion and Management, 2007, 48(10): 2638. DOI:10.1016/j.enconman.2007.04.018
[18]	MORTENSEN M, MINET R G. A two-stage cyclic fluidized bed process for converting hydrogen chloride to chlorine[J]. Chemical Engineering Science, 1996, 51(10): 2031. DOI:10.1016/0009-2509(96)00060-7
[19]	NOMURA S. Behavior of coalchlorine in coke making process[J]. International Journal of Coal Geology, 2010, 83(4): 423. DOI:10.1016/j.coal.2010.06.003
[20]	SLIGER T, KRAMLICH J, MARINOV N. Towards the development of a chemical kinetic model for the homogeneous oxidation of mercury by chlorine species[J]. Fuel Processing Technology, 2000(65/66): 423.
[21]	Fluent Inc. Fluent user's guide[EB/OL]. 2003. http://www.fluent.com.
[22]	JABER H, WEBB R L. Design of cooling towers by the effectiveness NTU method[J]. American Society of Mechanical Engineers Journal of Heat Transfer, 1989, 111: 837.
[23]	ALWAKED R, BEHNIA M. CFD simulation of wet cooling towers[J]. Applied Thermal Engineering, 2006, 26(4): 382. DOI:10.1016/j.applthermaleng.2005.06.018
[24]	中国人民共和国电力行业标准委员会. 冷却塔淋水填料、除水器、喷溅装置性能试验方法: DL/T 933—2005[S]. 北京: 中国电力出版社, 2005.
[25]	赵顺安. 冷却塔工艺原理[M]. 北京: 中国建筑工业出版社, 2015: 480. ZHAO Shunan. The principle of cooling towers[M]. Beijing: China Construction Industry Publishing, 2015: 480.
[26]	TERBLANCHE R, REUTER H C R, KROGER D G. Drop size distribution below different wet-cooling tower fills[J]. Applied Thermal Engineering, 2009, 29(8/9): 1552.
[27]	ALSHAMMIRI M. Evaporation rate as a function of water salinity[J]. Desalination, 2002, 150: 189. DOI:10.1016/S0011-9164(02)00943-8