2. 西南交通大学 力学工程学院,成都 610031;
3. 振动与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150001
2. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150001, China
配筋砌体剪力墙结构作为一种新型的结构体系,与钢筋混凝土结构相比,其造价低10%~18%,节省材料30%~50%,施工速度可提高25%以上,且配筋砌体剪力墙结构强度高、延性好、耗能能力强[1].对配筋砌块剪力墙的研究大致可分为三类:1)试验手段,分析配筋砌体剪力墙的承载能力影响因素,如竖向钢筋的数量及分布情况、水平钢筋、竖向压应力、边界约束情况等对构件承载力的影响[2-6];2)有限元等数值分析软件模拟配筋砌体剪力墙的破坏过程、破坏模式、破坏机理及承载能力[7-8];3)在大量试验数据的基础上统计分析构件的性能[9].这些研究主要是研究构件的承载能力及耗能能力,尚未见有人基于应变从宏观角度直接判定结构是否失效并建立相应失效判定准则.
现有研究表明,弯曲破坏配筋砌块剪力墙竖向钢筋上归一化的应变平方和值能反应结构的受力状态[10],且基于结构受力状态的方法可较好预测未知墙板的失效荷载[11].剪切破坏的配筋砌体剪力墙是否具有相似规律有待进一步研究.本文以低周往复荷载作用下发生剪切破坏的290 mm厚配筋砌块剪力墙试验数据[12]为研究对象,建立基于结构受力状态的配筋砌体剪力墙剪切失效判定准则.
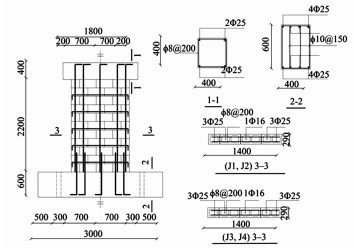
1 剪力墙模型和试验方案 1.1 剪力墙模型的制作与参数剪力墙由哈工大集团哈特新型建材制品厂提供的290厚MU20(名义值)混凝土小型空心砌块砌筑而成.其中,砌块的主规格为390 mm×290 mm×190 mm(已开槽),辅助块为190 mm×290 mm×190 mm(已开槽),其抗压强度平均值为19.21 MPa; 采用抗压强度平均值为20.86 MPa的混合砂浆砌筑;灌芯混凝土为微膨胀细石混凝土,其抗压强度平均值为12.85 MPa.剪力墙试验模型高2 200 mm,宽1 400 mm,竖向钢筋采用HRB335直径16 mm、25 mm钢筋,水平钢筋采用HPB235直径8 mm、10 mm钢筋,其构造参数见表 1,尺寸及配筋见图 1.
| 表 1 剪力墙模型构造参数 Table 1 Test parameters |
|
图 1 剪力墙模型构造 Figure 1 Geometry dimension and details of reinforcement |
采用力-位移混合控制加载机制:在剪力墙开裂之前以力控制加载,开裂之后以位移控制加载.首先在剪力墙顶部施加竖向力,当竖向力达到预定值(600 kN/800 kN,即正压力为1.5 MPa/2.0 MPa)时持荷,然后施加水平荷载,每级荷载增量为理论极限荷载的20%.在加载过程中,通过观察试件并监测位移曲线斜率是否发生变化来判断墙体是否开裂.当剪力墙开裂后,以位移控制加载,每级加载位移为开裂位移值,当水平荷载下降到极限水平荷载的70%或更低时,停止加载.加载装置和方案见图 2、3.

|
图 2 加载装置 Figure 2 Loading instruments |

|
图 3 加载方案 Figure 3 Loading steps |
总体来说,4片墙均表现出剪切破坏特征.当荷载较小时,首先在墙体根部灰缝处出现水平拉裂缝;随着横向荷载的增加,墙上出现沿砌块灰缝与砌块接触面的阶梯型斜裂缝,且裂缝的长度和宽度随着荷载的增加而缓慢发展;随着外荷载的进一步增加,墙体上出现贯通砌块的斜裂缝,并逐渐发展形成多条平行的X型交叉斜裂缝;随着外荷载继续增加,墙体中下部水平钢筋屈服,墙体的承载力下降,墙体上交叉斜裂缝的数量不再增加,裂缝的宽度和长度不断发展直到贯通.试验现象描述及分析见文献[12].
2 剪力墙受力状态分析归一化的应变平方和值可以用来反应结构的受力状态[10].为从理论上得到结构受力状态参数与荷载的关系曲线,本文分析了剪力墙在开裂前和开裂后两种状态下的受力状态.在开裂前,剪力墙处于弹性工作阶段,其刚度及受力面积基本保持不变,受力状态参数可表示为
| $ \begin{array}{l} {S_1} = \frac{{\sum {{\varepsilon ^2}} }}{{{{\left( {\sum {{\varepsilon ^2}} } \right)}_{\max }}}} = \frac{1}{{{{\left( {\sum {{\varepsilon ^2}} } \right)}_{\max }}}}{\left( {\frac{F}{{EA}}} \right)^2} = \\ \;\;\;\;\;\;\frac{1}{{{{\left( {\sum {{\varepsilon ^2}} } \right)}_{\max }}{{\left( {EA} \right)}^2}}}{F^2}. \end{array} $ | (1) |
式中:
| $ {a_1} = \frac{1}{{{{\left( {\sum {{\varepsilon ^2}} } \right)}_{\max }}{{\left( {EA} \right)}^2}}},有\;{S_1} = {a_1}{F^2}. $ | (2) |
开裂后,墙体的刚度及受力面积均发生变化,其受力状态可表示为
| $ \begin{array}{l} {S_2} = \frac{1}{{{{\left( {\sum {{\varepsilon ^2}} } \right)}_{\max }}}}\frac{{{{\left( {F - {F_{{\rm{cr}}}}} \right)}^2}}}{{{{\left( {E'A'} \right)}^2}}} + {S_{{\rm{cr}}}}=\\ \;\;\;\;\;\;\frac{1}{{{{\left( {\sum {{\varepsilon ^2}} } \right)}_{\max }}{{\left( {E'A'} \right)}^2}}}{\left( {F - {F_{{\rm{cr}}}}} \right)^2} + {S_{{\rm{cr}}}}, \end{array} $ | (3) |
式中:E′为墙体开裂后的弹性模量,A′为墙体开裂后的荷载受力面积,Fcr为墙体的开裂荷载,Scr为墙体开裂受力状态值.
剪力墙的弹性模量E′及受力面积A′会因为荷载的存在而持续减小,即
| $ {S_2} = {a_2}F{\left( {F - {F_{{\rm{cr}}}}} \right)^2} + {S_{{\rm{cr}}}}. $ | (4) |
对J1在正负向荷载作用下的竖向钢筋上的应变数据进行拟合,得到a1=1×10-6kN-2,a2=7× 10-8 kN-3.于是,剪力墙受力状态计算公式为
| $ S = \left\{ \begin{array}{l} {a_1}{F^2},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;F \le {F_{{\rm{cr}}}};\\ {a_2}F{\left( {F - {F_{{\rm{cr}}}}} \right)^2} + {S_{{\rm{cr}}}},\;\;\;\;\;F > {F_{{\rm{cr}}}}. \end{array} \right. $ | (5) |
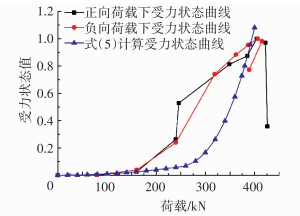
根据式(5)得到J1~J4的结构受力状态-荷载关系曲线, 与试验结果对比见图 4~7.按照式(5)计算得到的结构受力状态曲线与试验得到的受力状态曲线变化趋势一致,理论受力状态-荷载曲线与试验受力状态-荷载曲线略有差异,主要因为:1)进行理论推导的时候假定构件开裂前钢筋与砌体是完全刚性黏结的,未考虑两者之间的滑移;2)实测数据中包含着各种其他因素造成的误差;3)试验过程中有部分测点失效.式(5)能有效反映剪力墙整体的实时受力状态.
|
图 4 剪力墙J1的受力状态曲线 Figure 4 Stress state curve of Wall J1 |
|
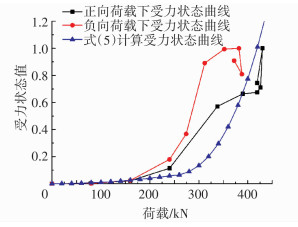
图 5 剪力墙J2的受力状态曲线 Figure 5 Stress state curve of Wall J2 |

|
图 6 剪力墙J3的受力状态曲线 Figure 6 Stress state curve of Wall J3 |

|
图 7 剪力墙J4的受力状态曲线 Figure 7 Stress state curve of Wall J4 |
得到剪力墙的受力状态随外荷载的变化规律后,需要确定剪力墙的开裂荷载、失效荷载及极限荷载.剪力墙开裂时,主要表现为混凝土受拉破坏;剪力墙剪切失效是以墙体上产生斜裂缝为判定标准的,即墙上的主拉应力超出墙体的抗拉强度;而极限承载力则与墙体中水平钢筋的布置密切相关.本文根据构件不同受力阶段的破坏机理,提出基于受力状态的开裂、失效及承载能力包络线的概念,一旦剪力墙的受力状态曲线超出相应的包络线范围,则剪力墙开裂、失效或达到极限承载力.根据量纲分析方法,基于受力状态的剪力墙开裂包络线Scr定义为
| $ {S_{{\rm{cr}}}} = \frac{{{C_{{\rm{cr}}}}}}{{kF}}. $ | (6) |
式中:Ccr为剪力墙开裂承载能力值,其量纲为[N];Scr为剪力墙开裂受力状态值,是一个无量纲的物理量;F为外荷载,其量纲为[N];k为无量纲系数.
定义剪力墙失效和极限承载能力包络线Sfail、Su:
| $ {S_{{\rm{fail}}}} = \frac{{{C_{{\rm{fail}}}}}}{{kF}}, $ | (7) |
| $ {S_{\rm{u}}} = \frac{{{C_{\rm{u}}}}}{{kF}}, $ | (8) |
式中Cfail、Cu表示剪力墙的失效及极限承载能力值.
剪力墙的开裂、失效和极限承载能力值是计算包络线的关键.本文根据剪力墙在不同阶段的破坏机理,给出相应的承载力计算公式.
当剪力墙上的拉应力超出了混凝土的抗拉强度时,剪力墙开裂,即
| $ {\sigma _{\rm{t}}} - {\sigma _{\rm{N}}} = {f_{\rm{t}}}, $ | (9) |
式中:σt为由横向力在剪力墙底部产生的拉应力,σN为剪力墙竖向压应力,ft为剪力墙的抗拉强度设计值.
由试验现象知道,第一条裂缝通常出现在墙体底部的灰缝处,于是有
| $ {\sigma _{{\rm{t}}/{\rm{c}}}} = \frac{M}{W} = \frac{{6FH}}{{b{B^2}}}. $ | (10) |
式中:b为墙体厚度,B为墙体宽度,H为水平力的作用点到墙底灰缝处的距离,σt/c为由横向力产生的拉/压应力.将式(10)带入式(9)可得到剪力墙开裂承载力值计算式为
| $ {C_{{\rm{cr}}}} = \frac{{b{B^2}\left( {{f_{\rm{t}}} + {\sigma _{\rm{N}}}} \right)}}{{6H}}. $ | (11) |
当剪力墙失效时,剪力墙上的剪应力超过灌芯砌体的抗剪强度,同时考虑竖向压应力对墙体抗剪强度的影响有
| $ {\sigma _{\rm{v}}} = {f_{{\rm{vg}},{\rm{m}}}} + \alpha {\sigma _{\rm{N}}}. $ | (12) |
式中:σv为剪切应力,σN为竖向压应力,α为竖向压应力对剪切强度的影响系数,fvg, m为灌芯砌体抗剪强度.于是,截面上失效承载力值为
| $ {C_{{\rm{fail}}}} = {\sigma _{\rm{v}}}A = \left( {{f_{{\rm{vg}},{\rm{m}}}} + \alpha {\sigma _{\rm{N}}}} \right)b{h_0}, $ | (13) |
式中h0为墙体的有效高度.
当达到承载能力极限时,墙体中水平钢筋屈服,极限承载力为
| $ {C_{\rm{u}}} = {C_{{\rm{fail}}}} + {f_{{\rm{yh}}}}{A_{{\rm{sh}}}}. $ | (14) |
式中:fyh为水平钢筋的抗拉强度设计值,Ash为水平钢筋的面积.
根据砌体结构设计规范[13],混凝土灌芯砌块砌体的抗拉强度ft和抗剪强度分别为:
| $ {f_{\rm{t}}} = 0.056\sqrt {{f_{{\rm{ce}}}}} , $ | (15) |
| $ {f_{{\rm{vg}},{\rm{m}}}} = 0.2f_{{\rm{gm}}}^{0.55}. $ | (16) |
式中:fce为砂浆的抗压强度设计值,fgm为灌芯砌体的抗压强度.
将J1在正负向荷载下的开裂荷载平均值带入式(6),再结合式(11)计算剪力墙开裂承载能力Ccr及式(5)计算剪力墙开裂受力状态值Scr,可以确定无量纲系数k=4.25.同样的将J1在正负向荷载作用下的剪力墙失效荷载平均值带入式(5)、(7)并结合式(13)有α=0.2.
综上有剪力墙基于受力状态的开裂、失效及极限承载力包络曲线为
| $ \left\{ \begin{array}{l} {S_{{\rm{cr}}}} = \frac{{{C_{{\rm{cr}}}}}}{{kF}} = \frac{{b{B^2}\left( {{f_{\rm{t}}} + {\sigma _{\rm{N}}}} \right)}}{{6kHF}},\\ {S_{{\rm{fail}}}} = \frac{{{C_{{\rm{fail}}}}}}{{kF}} = \frac{{\left( {{f_{{\rm{vg}},{\rm{m}}}} + 0.2{\sigma _{\rm{N}}}} \right)b{h_0}}}{{kF}},\\ {S_{\rm{u}}} = \frac{{{C_{\rm{u}}}}}{{kF}} = \frac{{\left( {{f_{{\rm{vg}},{\rm{m}}}} + \alpha {\sigma _{\rm{N}}}} \right)b{h_0} + kF{f_{{\rm{yh}}}}{A_{{\rm{sh}}}}}}{{kF}}. \end{array} \right. $ | (17) |
受力状态曲线(式(5))与式(17)交点对应的外荷载即为剪力墙的开裂、失效、极限荷载.
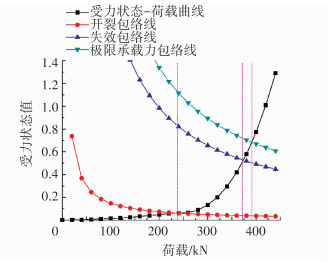
为进一步验证上述判定准则的准确性,剪力墙J1~J4的受力状态-荷载关系曲线及包络线见图 8~11.
|
图 8 剪力墙J1受力状态曲线与包络曲线 Figure 8 Stress state curve and capacity envelops of Wall J1 |
|
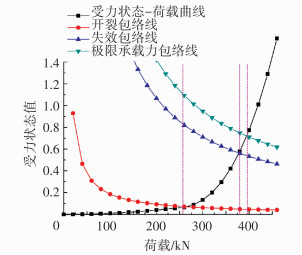
图 9 剪力墙J2受力状态曲线与包络曲线 Figure 9 Stress state curve and capacity envelops of Wall J2 |

|
图 10 剪力墙J3受力状态曲线与包络曲线 Figure 10 Stress state curve and capacity envelops of Wall J3 |
|
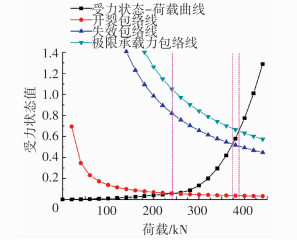
图 11 剪力墙J4受力状态曲线与包络曲线 Figure 11 Stress state curve and capacity envelops of Wall J4 |
根据剪力墙的受力状态-荷载曲线与包络线相交得到的开裂、失效及极限荷载,与试验结果的对比见表 2,且用式(18)来判断准则的预测精度:
| $ e = \left| {\frac{{F - {F_{{\rm{ave}}}}}}{{{F_{{\rm{ave}}}}}}} \right| \times 100\% , $ | (18) |
| 表 2 计算结果与试验结果对比 Table 2 Comparison between calculated and test results |
式中:F为曲线相交得到的荷载,Fave为正负向荷载下的试验荷载平均值.
由表 2可看出,基于受力状态曲线结合包络曲线计算得到的荷载与试验结果的误差均在10%以内.
本文提出的方法与现有的基于截面应力状态的分析方法有着本质的区别:该方法主要是得到构件在外荷载作用下的实时受力状态,判断构件的受力状态与各种承载力(包络线)之间的关系来确定相应的开裂、失效和极限荷载.一旦构件的受力状态超过相应的包络线,则构件发生相应的破坏,因此该方法也为结构健康监测提供一个新途径.
4 结论1) 墙体中竖向钢筋上的归一化的应变平方和值可以用来从宏观上反应构件的受力状态.
2) 基于结构受力状态曲线结合承载力包络线可以用来确定剪切破坏的配筋砌块剪力墙的开裂荷载、失效荷载及极限荷载,且有较高精度.
3) 研究结果进一步拓展了结构受力状态分析理论的应用,并拓展了试验数据在结构分析中的应用方式.
| [1] |
王凤来, 张厚, 唐岱新. 论我国墙用混凝土砌块产业发展的教训和砌块整浇墙技术[J]. 建筑砌块与砌块建筑, 2010(6): 4-9. WANG Fenglai, ZHANG Hou, TANG Daixin. Lessons of concrete masonry blocks industry applied in walls and the technology of fully grouted concrete masonry wall[J]. Construct masonry block and masonry buildings, 2010(6): 4-9. |
| [2] |
新型砌体结构体系与墙体材料(上册)[M]. 哈尔滨: 中国建材工业出版社, 2010.
|
| [3] |
赵艳, 王凤来, 张厚, 等. 砌块整浇墙骨架曲线影响因素分析[J]. 哈尔滨工业大学学报, 2013, 45(8): 16-22. ZHAO Yan, WANG Fenglai, ZHANG Hou, et al. Analysis of influencing factors on the skeleton curve for fully grouted reinforced masonry shear walls[J]. Journal of Harbin institute of technology, 2013, 45(8): 16-22. DOI:10.11918/j.issn.0367-6234.2013.08.003 |
| [4] |
ZHAO Y, WANG F L. Experimental studies on behavior of fully grouted reinforced-concrete masonry shear walls[J]. Earthquake Engineering and Engineering Vibration, 2015, 14: 743-757. DOI:10.1007/s11803-015-0030-5 |
| [5] |
BANTING B, EI-DAKHAKHNI W. Seismic design parameters for special masonry structural wall detailed with confined boundary elements[J]. Journal of Structural Engineering, 2014, 140(10): 04014067. DOI:10.1061/(ASCE)ST.1943-541X.0000980 |
| [6] |
EHSAN M, FRANKLIN L M, AHMAD A H. Nonlinear finite element modeling of reinforced masonry shear walls for bidirectional loading response[J]. Finite Elements in Analysis and Design, 2014, 84: 44-53. DOI:10.1016/j.finel.2014.02.001 |
| [7] |
EZZELDIN M, WIEBE L D, EI-DAKHAKHNI W. Numerical modelling of reinforced concrete block structural wall buildings under seismic[C]//International structural specialty conference. London: [s. n. ], 2016: 1-10.
|
| [8] |
AHMAD S S, WESSAM M H, EI-DAKHAKHNI W. Scoring models for reinforced masonry shear wall maximum displacement prediction under seismic loads[J]. Engineering Structures, 2017, 136: 511-522. DOI:10.1016/j.engstruct.2016.12.036 |
| [9] |
VOON K C, INGHAM J M. Experimental In-plane shear strength investigation of reinforced concrete masonry walls[J]. Journal of structural engineering, 2006, 132(3): 400-408. DOI:10.1061/(ASCE)0733-9445(2006)132:3(400) |
| [10] |
黄艳霞. 基于结构受力状态的砌体墙片细胞自动机分析方法[D]. 哈尔滨: 哈尔滨工业大学, 2014. HUANG Yanxia. Cellular automata method of masonry structure analysis based on structural stressing state[D]. Harbin: Harbin institute of technology, 2014. |
| [11] |
HUANG Y X, ZHANG Y, ZHANG M, et al. Method for predicting the failure load of masonry wall panels based on generalized strain-energy density[J]. Journal of Engineering Mechanics, 2014, 140(8): 4014061-4014066. DOI:10.1061/(ASCE)EM.1943-7889.0000771 |
| [12] |
丁向奎. 低周往复荷载下290厚砌块整浇墙剪切破坏模式试验研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. DING Xiangkui. Experimental study on shear failure mode of 290 concrete-block casting wall under low-cyclic loading[D]. Harbin: Harbin institute of technology, 2014. |
| [13] |
砌体结构设计规范: GB 50003—2011[S]. 北京: 中国建筑工业出版社, 2011.
|
 2018, Vol. 50
2018, Vol. 50


