众所周知,地下工程涉及众多的不确定性,深地环境面临的条件将更加复杂.深部岩石受到的地应力高,加之经历地质构造作用的影响,深部岩石内部又积蓄了大量的能量;且不同地区、不同深度的岩石介质自身微结构差异显著.在深部开采时,这些能量如果突然释放,容易发生岩爆,造成人员伤亡,设备损坏等损失.因而,对于不同应力水平下岩石蓄能状态,以及不同微结构的岩石在受载过程中能量演化规律的研究颇有意义.就项目依托金矿勘探的结果而言,在深度1 300 m左右或是深部成矿带上盘的岩石异质性突出且蚀变严重,岩芯出现矿物质黏结面和饼化现象.本文主要针对金属矿开采过程中遇到的异质性突出,含有裂隙黏结面的岩石介质进行受载破坏能量演化规律的研究与讨论.
已有学者从不同角度分析岩石的破碎,其中岩石含能破坏近年来受到越来越多的关注[1-20].岩石受力破坏的全过程中,能量经历了积聚、耗散和释放等过程,能量的耗散机理主要有裂纹的发展、颗粒间的摩擦、晶粒间结构的自适应调整等.目前,对于岩石能量的研究主要集中在完整岩石试样受载破坏的能量演化规律中,但是金属矿开采过程中常常遇到蚀变严重、异质性突出、含有裂隙黏结面的岩体,这类异质性凸显的岩石受载后能量演化有何特征值得研究探讨.
由于深部建井过程中开挖卸载后的围岩大多处于低围压状态,而对于开挖空间围岩强度的评估,按照蔡明等[20]的观点,开挖后围岩的受力状态比较接近单轴压缩受力状态,在知道岩石的单轴抗压强度的基础上即可对围岩强度做出经验性的判断.本文针对含黏结面的花岗岩试样在单轴循环受载过程中能量的演化规律进行初步研究与探讨,研究成果能够为建井工程提供参考和借鉴.
1 试验 1.1 试验力学系统本次试验所采用的刚性压力试验机为AW2000型单轴液压伺服机,全程计算机控制,可实现自动数据采集和处理;机架采用实心刚架,储存的弹性能小.声发射设备是沈阳计算机技术研究设计院设计生产的AE21C声发射检测系统,如图 1所示.

|
图 1 压力装置与声发射系统 Figure 1 Pressure device and acoustic emission system |
为了研究带黏结面花岗岩试样在受载过程中的能量变化趋势,加工花岗岩标准试样直径50 mm,高100 mm.本次试验花岗岩试样黏结面的形成主要是由于该花岗岩在成岩过程中受侵蚀而存在一个被矿物质黏结的斜面,图 2的线条标记处即为矿物质黏结面的位置.在伺服刚性压力试验机上采用应变控制的方式进行循环加卸载,加载速率0.01 mm/min,卸载速率0.02 mm/min.加卸载过程中,采用声发射装置对岩石破裂的声发射信号进行检测.利用谢和平等[1]的能量计算方法,计算整个加载过程中各部分的能量并探讨其随应力变化的规律.具体计算方法如图 3所示,加载曲线下的应力-应变面积积分可以看作是外界输入单元体积岩块的总能量,卸载曲线下的面积积分表示单元体积岩块可释放的弹性能,二者之差即为此次加卸载单元体积岩石的耗散能.

|
图 2 试验岩样 Figure 2 Test rock specimen |

|
图 3 能量计算方法 Figure 3 Energy calculation method |
目前,岩石力学研究领域的学者从热力学第一定律的角度出发,不考虑热交换,将外界输入岩体的能量U分为两部分,即U=Ud+Ue.Ud为耗散能,Ue为可释放弹性能[1].弹性能的理解较为简单,即岩石储存的能量中可以作为高质量能量而释放做功的一部分能量.耗散能则是用于形成岩石材料内部的损伤和塑性变形[1],塑形变形易为理解,岩石内部损伤的主要表现形式是裂纹的生成以及颗粒间的摩擦[3-5].这几种耗散机制将岩石内部先前存储的能量耗散掉一部分,且这种变化过程是不可逆的.
2 结果分析 2.1 应力-应变曲线下的能量统计结果试验中花岗岩的循环加卸载应力-应变曲线如图 4所示,各能量的变化趋势如图 5所示.在应力还不太高的第5次卸载之初发生黏结面局部的破坏.各次加卸载的能量变化统计如表 1所示.

|
图 4 循环加卸载应力-应变曲线 Figure 4 Cyclic loading and unloading stress-strain curve |

|
图 5 加载过程中花岗岩各部分能量随应力变化 Figure 5 Energy of each part of the granite changes with stress during the loading process |
| 表 1 单元体积岩样各次加卸载的能量变化 Table 1 Energy change in unit volume rock specimen during loading and unloading |
图 5中的岩石单元体体积的各能量大小指的是随着加载过程应力的逐步增加而累积的单元体各能量大小.从各能量的变化趋势可以看出,各能量随着应力水平的增加而增长,经拟合发现峰值前各能量随应力的变化趋势大致呈指数形式变化,弹性能在峰值点前达到最大值,之后开始降低;相反,耗散能在峰值以后快速增加,反映了花岗岩整体结构的损坏.
弹性能的积累容易造成岩石的冲击破坏.因而将“弹性能/输入岩石的总能”定义为“有效能比”,“有效能比”可以看作同一种岩石不同应力状态下的储能水平.本次试验岩样的“有效能比”在压密阶段和弹性阶段逐渐上升至72%,蓄能水平逐步上升,在黏结面部位破坏时迅速下降至60%,表明结构的局部破坏使得蓄能水平降低,峰值强度时再次下降至40%,表明结构在受压方向整体破坏.
由图 5可以看出,“有效能比”在第5次卸载之前持续升高,主要是因为应力作用下岩石内部结构被压密,岩石结构的自适应调整使得岩石的刚度增加从而蓄能水平逐渐提高.“有效能比”在第5次卸载之初即花岗岩黏结面局部破坏时迅速降低,峰值强度时再次降低.这表明应力造成了岩石黏结面附近内部结构的损伤,使得内部结构发生了变化,而岩石的储能水平随着岩石内部结构的改变而改变.
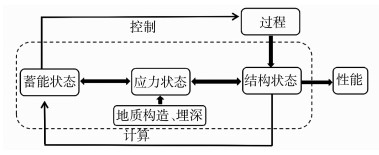
与能量相关的范畴不仅涉及外界的应力水平也涉及岩石自身的结构状态.地质构造和埋深往往是应力水平的体现,对于岩石的结构状态也必须关注.例如对于金属矿常见的花岗岩而言,裂隙分布、蚀变程度以及矿物种类中长石和石英的含量多少, 以及其结晶颗粒的大小等都决定了岩石自身的结构状态.应力水平、能量以及结构状态的关系如图 6所示.
|
图 6 岩石的应力状态、能量、结构之间的关系 Figure 6 Relationship between the stress state, energy and structure of the rock |
结合以前研究人员的成果及本次试验得到的规律可知,就岩石自身结构而言,岩石异质性越突出对受载形变越敏感,则岩石自身结构越易损伤.同时,在地质构造作用下的蚀变程度会越高,则在开采过程中大部分能量用于耗散而不会大量的积累,因为往往在能量还未积累至较大值,由于局部部位的破坏,能量将被释放.与此同时这种破坏改变了岩体原来的结构状态,降低岩石的储能水平,所以,单从能量角度分析,造成冲击性破坏的概率相对就小,当然冲击破坏同时也要考虑缺陷部位破坏时所对应的应力水平大小,对应的应力水平越大,冲击的概率相对较大.例如对于深部的岩石,尽管应力水平很高,但如果工程岩体蚀变严重,较为破碎,能量的释放有时也不一定会很剧烈.而结构越完整的岩石则储能水平越好,能量不易释放,当应力水平达到临界值时,有时深度不一定很深,能量突然释放反而易造成冲击性的破坏.对于蚀变严重区域的岩石由于这种异质性的突出,岩石的抗拉性能较弱,围岩往往易出现片裂现象[20].
2.2 声发射结果分析目前完整花岗岩破裂的声发射研究很多,试验和理论成果相对比较成熟.对于完整的花岗岩破裂时,声发射检测到的能量以及计数率基本上表现为由小到大变化的过程性,并且体现出破裂进展的阶段性.本文基于先前成果研究含黏结面花岗岩破裂的能量变化特征.图 7为试验室对于较为完整不含黏结面的均质绢英花岗岩单轴加卸载试验的检测结果,该岩样取自在建主井730 m的浅部,岩样均质性较好但脆性突出.试验只关注峰前阶段加卸载3次.

|
图 7 较完整花岗岩的应力-应变及声发射信号与应力值对应关系 Figure 7 Stress-strain curves of relatively intact granite and corresponding relation between acoustic emission signal and stress values |
所得的规律与大多数学者基本一致,即声发射参数基本上表现出由小到大变化的过程性,也体现出破裂进展的阶段性,岩样整体破坏时释能率和计数率最大.而黏结面的存在与这种常规的变化规律不符.
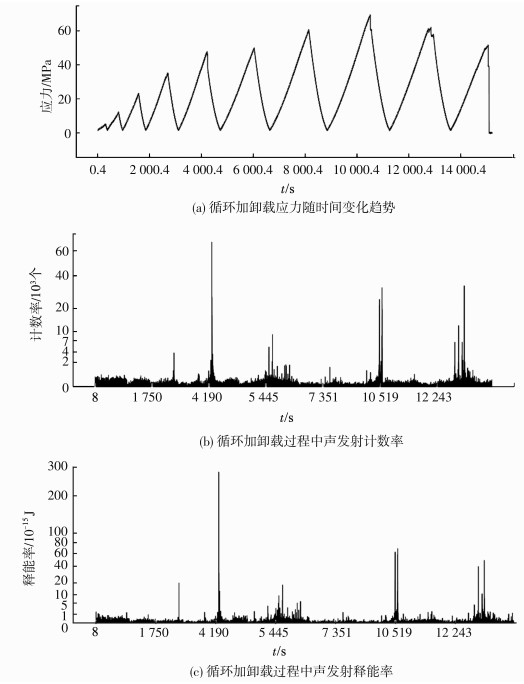
对于带黏结面的花岗岩,如图 8,由声发射的结果可知,声发射计数率与释能率的变化规律基本相同,第4次循环加载至应力接近40 MPa时,出现第1次的声发射信号突增,但是增幅不大.循环加载次数第5次完成时,在随后的卸载之初即4 190 s附近时黏结面部位发生局部破坏,计数率和释能率瞬时增加.对比第5次局部破坏与第8次峰值强度即10 519 s附近时的声发射计数率与释能率发现,局部破坏的声发射能量释放比峰值强度时声发射检测到的能量释放还要多.本次试验对象黏结面的面积较大,所以,黏结面破坏的释能明显.
|
图 8 声发射特征值统计 Figure 8 AE eigenvalue summary |
加载与卸载过程对比发现,加载过程中一般当应力超过上一次加载的应力时,才出现明显的声发射现象,应力水平较低时,卸载过程中一般不会有声发射现象或声发射现象基本可以忽略.但是当应力水平达到一定值时,即当花岗岩积聚的弹性能超过了局部破坏的耗散能时,花岗岩在卸载时会发生较易被感知的脆性破坏.如第5次卸载之初,产生瞬时的、集中的、破坏声音分辨明显的声发射现象.
本次试验的花岗岩在第5次卸载之初破坏时,对应的时间大约是4 190 s,由声发射释能率和计数率可以看出,此后至峰值前岩石的释能率和计数率在经过第6次加载调整后几乎变得很低.就本次试验的带黏结面花岗岩而言,结合应力-应变图可知,存在黏结面薄弱区域的岩石在黏结面局部破坏后,岩石内部的结构经过自我调整其承载能力依旧可以提升直至整体破坏.但是从声发射释能率来讲,黏结面部位局部破坏的释能率比峰值点破坏要高,因为局部破坏后岩石结构的改变影响了能量的积聚效率.
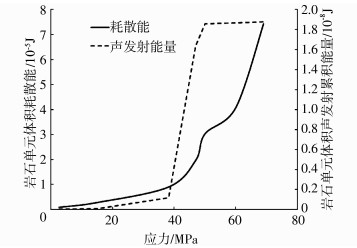
2.3 声发射能量与耗散能的统计分析利用声发射设备对花岗岩在加载过程释放的能量中被声发射仪器检测到的能量进行不同应力水平下的累积统计,结果如图 9所示.
|
图 9 不同应力水平下的声发射能量累积 Figure 9 AE energy accumulate at different stress level |
花岗岩在加载之初时,声发射检测到的能量释放并不大.就本次试验的带黏结面花岗岩而言在加载至40~50 MPa时,岩石黏结面部位出现了破裂,可以听到明显的碎裂声,在这一短暂的过程中,由声发射累积能量图可以看出,声发射设备检测到了大量的能量释放.尽管花岗岩的承载力仍在提升,但此后,声发射检测到的能量累积变得较为缓慢,类似于加载之初弹性阶段的声发射变化趋势,表明单轴压缩条件下,岩石结构在局部破坏后经过自我调整的结构受载的声发射表现形式类似于弹性阶段的表现形式.
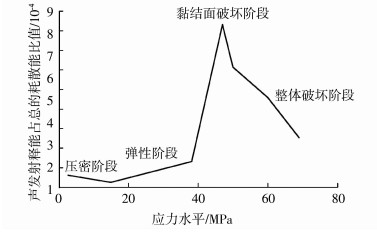
本次试验所采用的声发射仪器收集到的能量只占耗散能的很小一部分,但由于声发射检测到的能量属于内部结构损伤耗散掉能量的一部分,所以,就整个过程而言,“累积的声发射能量”与“总的耗散掉的能量”的比值能够反应出声发射仪器随着应力水平,以及岩石结构状态变化的检测效率.所以,引入声发射检测效率值,由图 10的声发射检测效率看,在压密阶段声发射的效率逐渐降低,该阶段的表现反映了裂隙闭合率的降低与岩石自身刚度的增加[21];弹性阶段声发射效率稳中有升,表明微裂纹的发展缓慢,能量耗散很少,主要表现为弹性能的积累;在黏结面位置局部破裂时声发射效率达到最高值;随后在整体破坏阶段,尽管又发生破裂,声发射的效率值没有再次上升反而逐渐呈下降趋势,表明黏结面附近的破坏对岩石刚度的影响较为显著,从而降低了岩石的储能效率,所以,出现了在峰值强度时检测到的声发射能量低于黏结面破坏的现象.就本次试验对象而言,黏结面的面积较大,黏结面附近的破坏对岩石的刚度影响明显,黏结面局部破坏时释放出的能量比其他阶段更易被检测到.
|
图 10 声发射检测效率 Figure 10 Acoustic emission detection efficiency |
对于岩石的卸载已经有过试验研究,其卸载破裂应力水平低于加载时的强度[9].本次试验黏结面部位的破裂也发生在第5次卸载之初.所以,从能量演化的角度简单分析讨论加、卸载破裂应力的不同.对于一般的岩石,在弹性阶段结束以前耗散能几乎很小,可忽略.本次的讨论假设弹性阶段以前的耗散能不计,即外界输入的能量全部以弹性能储存,则对于火成岩类的硬脆性花岗岩,可以粗略认为弹性阶段以前积累的弹性能的释放造成了岩石的破坏,即“弹性能转换为耗散能”.
目前,绝大多数岩石的弹性能积累在应力-应变曲线峰值前远高于耗散能,如图 11所示.假如A点是峰值点,峰值点A对应的耗散能大小,就与B点所对应的弹性能大小一样.所以,在理想条件下(没有约束,能量自由释放且转化率为100%),加载至B点时突然卸载,如果弹性能全部释放转换为耗散能,则在B点卸载时,在较小的应力水平下,便可以使岩石发生效果类似于峰值强度时的破坏,因而表现的外在形式就是卸载对应岩石的应力水平较低.然而由于边界约束的存在,以及能量转化率不可能100%,卸载时的现实条件应该介于A、B两点之间.

|
图 11 不同能量随应力变化趋势示意 Figure 11 Changing trends of different energies as stress changes |
B点的意义在于:应力状态从此刻以后继续增加,完整的岩石内部积累的弹性能在快速释放的条件下,已经足以使得岩石发生类似于峰值强度时的破坏,但是由于加载方式所对应的边界约束条件的限制,以及弹性能的转换不可能达到百分之百的效率,卸载时破坏点应该发生在A、B两点之间,卸载对应的应力低于加载强度,但是一定大于B点对应的应力大小.
从本次试验加卸载能量变化的图 5可以看出,黏结面的局部破坏发生在第5次卸载之初,而上一次积累的弹性能与局部破坏时的耗散能大小几乎是相等的.此外,如图 5所示,几乎所有前一次积累的弹性能与下一次的耗散能大小相当.换言之对于本次试验的这块花岗岩,每一次耗散能的增加,几乎都是在跟循着前一次加载时弹性能累积的脚步,只要弹性能累积到一定水平,破坏便会产生.
4 结论1) 定义了“有效能比”(累积弹性能/输入岩石的总能).“有效能比”的变化规律在一定程度上能够反映岩石内部结构与储能水平的变化;且黏结面破坏后,岩石在一定程度上仍可储能.
2) 从整个加载过程来看,本次试验花岗岩黏结面部位破坏的声发射释能率高于峰值强度时的声发射释能率.黏结面局部破坏时的声发射表现出集中性、突发性的特征,峰值强度时声发射释能率相对较低,集中性相对不明显.
3) 应力水平较低时,卸载过程中的声发射现象基本可以忽略,但是当花岗岩积聚的弹性能超过了黏结面薄弱部位破坏的耗散能时,花岗岩在卸载时会发生较易被感知的脆性破坏.
4) 由于声发射检测到的能量属于耗散能的一部分,定义“声发射检测效率”(声发射累积能量/累积耗散能),结合本次试验发现“声发射检测效率”在压密阶段降低,弹性阶段升高,黏结面部位破坏时达到峰值,之后直至峰值强度持续降低.
5) 就岩石自身结构而言,相同应力下异质性越突出的岩石开采过程中储存的能量越容易被耗散,所以,造成冲击性破坏的概率一般会变小.结构越完整、致密、均一的岩石储能水平越好,当应力水平达到临界值时,有时深度不一定很深,能量突然释放,反而可能造成冲击破坏.
| [1] |
谢和平, 鞠杨, 黎立云, 等. 岩体变形破坏过程的能量机制[J]. 岩石力学与工程学报, 2008, 27(9): 1729-1740. XIE Heping, JU Yang, LI Liyun, et al. Energy mechanism of deformation and failure of rocks[J]. Chin J of Rock Mech Eng, 2008, 27(9): 1729-1740. |
| [2] |
BAŽANTZ P. Analysis of work-of-fracture method for measuring fracture energy of concrete[J]. Journal of Engineering Mechanics, 1996, 122(2): 138-144. DOI:10.1061/(ASCE)0733-9399(1996)122:2(138) |
| [3] |
HAMIEL Y, LYAKHOVSKY V, BEN-ZION Y. The elastic strain energy of damaged solids with applications to non-Linear deformation of crystalline rocks[J]. Pure and Applied Geophysics, 2011, 168(12): 2199-2210. DOI:10.1007/s00024-011-0265-7 |
| [4] |
CATES M E, WITTMER J P, BOUCHAUD J P, et al. Jamming force chains and fragile matter[J]. Phys Rev Lett, 1998, 81(9): 1841-1844. DOI:10.1103/PhysRevLett.81.1841 |
| [5] |
DAVIES T R H, MCSAVENEY M J, BOULTON C J. Elastic strain energy release from fragmenting grains: Effects on fault rupture[J]. Journal of Structural Geology, 2012, 38(5): 265-277. DOI:10.1016/j.jsg.2011.11.004 |
| [6] |
HAZZARD J F, YOUNG R P, MAXWELL S C. Micromechanical modeling of cracking and failure in brittle rocks[J]. Journal of Geophysical Research Solid Earth, 2000, 105(B7): 16683-16697. DOI:10.1029/2000JB900085 |
| [7] |
GAZIEV E. Rupture energy evaluation for brittle materials[J]. International Journal of Solids & Structures, 2001, 38(42): 7681-7690. DOI:10.1016/S0020-7683(01)00037-3 |
| [8] |
QUR T, ZHANG Z J, ZHANG P, et al. Generalized energy failure criterion[J]. Scientific Reports, 2016. DOI:10.1038/srep23359 |
| [9] |
华安增, 孔园波, 李世平, 等. 岩块降压破碎的能量分析[J]. 煤炭学报, 1995, 20(4): 389-392. HUA Anzeng, KONG Yuanbo, LI Shiping, et al. Energy analysis of depressurized rock fracture[J]. China Coal Soc, 1995, 20(4): 389-392. DOI:10.13225/j.cnki.jccs.1995.04.012 |
| [10] |
HOEK E, MARTIN C D. Fracture initiation and propagation in intact rock-A review[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(4): 287-300. DOI:10.1016/j.jrmge.2014.06.001 |
| [11] |
CARPINTERI A, CHIAIA B, NEMATI K M. Complex fracture energy dissipation in concrete under different loading conditions[J]. Mechanics of Materials, 1997, 26(2): 93-108. DOI:10.1016/S0167-6636(97)00022-7 |
| [12] |
尤明庆, 华安增. 岩石试样破坏过程的能量分析[J]. 岩石力学与工程学报, 2002, 21(6): 778-781. YOU Mingqing, HUA Anzeng. Energy analysis of failure process of rock specimens[J]. Chinese J of Rock Mech Eng, 2002, 21(6): 778-781. |
| [13] |
HORⅡ H, NEMAT-NASSER S. Compression-induced microcrack growth in brittle solids: Axial splitting and shear failure[J]. Journal of Geophysical Research Solid Earth, 1985, 90(B4): 3105-3125. DOI:10.1029/JB090iB04p03105 |
| [14] |
LOCKNER D A, BYERLEE J D, KUKSENKO V, et al. Quasi-static fault growth and shear fracture energy in granite[J]. Nature, 1991, 350(6313): 39-42. DOI:10.1038/350039a0 |
| [15] |
MOORE D E, LOCKNER D A. The role of microcracking in shear-fracture propagation in granite[J]. Journal of Structural Geology, 1995, 17(1): 95-111. DOI:10.1016/0191-8141(94)E0018-T |
| [16] |
黄达, 黄润秋, 张永兴. 粗晶大理岩单轴压缩力学特性的静态加载速率效应及能量机制试验研究[J]. 岩石力学与工程学报, 2012, 2: 245-255. HUANG Da, HUANG Runqiu, ZHANG Yongxing. Experimental investigation on statistic loading rate effects on mechanical properties and energy mechanism of coarse crystal grain marble under uniaxial compression[J]. Chinese J of Rock Mech Eng, 2012, 2: 245-255. DOI:10.3969/j.issn.1000-6915.2012.02.003 |
| [17] |
张志镇, 高峰. 单轴压缩下岩石能量演化的非线性特性研究[J]. 岩石力学与工程学报, 2012, 31(6): 1198-1207. ZHANG Zhizhen, GAO Feng. Research on nonlinear characteristics of rock energy evolution under uniaxial compression[J]. Chin J of Rock Mech Eng, 2012, 31(6): 1198-1207. |
| [18] |
WANG J A, PARK H D. Comprehensive prediction of rockburst based on analysis of strain energy in rocks[J]. Tunnelling & Underground Space Technology Incorporating Trenchless Technology Research, 2001, 16(1): 49-57. DOI:10.1016/S0886-7798(01)00030-X |
| [19] |
尤明庆, 华安增. 岩石试样单轴压缩的破坏形式与承载能力的降低[J]. 岩石力学与工程学报, 1998, 3: 292-296. YOU Mingqing, HUA Anzeng. Damage forms and bearing capacity of rock specimen uniaxial compression[J]. Chin J of Rock Mech Eng, 1998, 3: 292-296. |
| [20] |
CAI M. Practical estimates of tensile strength and hoek-brown strength parameter m, i of brittle rocks[J]. Rock Mechanics & Rock Engineering, 2010, 43(2): 167-184. DOI:10.1007/s00603-009-0053-1 |
| [21] |
ZHAO X G, CAI M, WANG J, et al. Objective determination of crack initiation stress of brittle rocks under compression using ae measurement[J]. Rock Mechanics & Rock Engineering, 2015, 48(6): 2473-2484. DOI:10.1007/s00603-014-0703-9 |
 2018, Vol. 50
2018, Vol. 50


