2. 情感计算与先进智能机器安徽省重点实验室(合肥工业大学),合肥 230009
2. Affective Computing and Advanced Intelligent Machines Key Laboratory(Hefei University of Technology), Hefei 230009, China
在人机交互的过程中,面向个体情感的分类与识别技术受到了广泛关注,并获得了较为显著的成果.众所周知,对用户的情感类型进行准确判断是提升交互体验的关键[1].然而,按照情感认知的相关理论,情感产生过程会受到个体认知因素的影响,对于同一外界刺激而言,不同的个体有不同的理解.用户之间存在的这种个体差异性,导致机器往往无法有效识别出其真实情感.Ju-Chiang Wang等以个体差异性为依据,采用高斯混合模型(Gaussian mixture model,GMM)描述了底层特征与高层情感状态之间的映射规则,能够进一步获得情感感知的主观性[2].Hemandez等提出了一种基于OCC认知的情感映射机制,并将其合理地应用于移动机器人智能辅导系统中,结果表明该情感映射机制对和谐的人机交互具有促进作用[3].可见,通过结合个性化认知进行情感分析将有助于突破性地提升情感识别结果,成为了许多研究者关注的焦点.
目前,大多数现有的方法侧重于围绕离散情感状态展开分析,即仅识别特定种类的情感状态(例如:高兴、厌恶和惊讶等)[4].然而在自然交互中,人类的情感状态是连续发生且多变的,离散情感模型无法准确地表达人类的情感变化,对实现个体情感分类映射有很大的局限性[5].基于维度论的情感空间模型考虑到了人类情感的连续性和多维度分布特点,能够更好地表达和模拟情感状态[6].情感的维度论认为几个维度组成的空间包括了人类所有的情绪,按照情绪所固有的某些特性,如动力性、激动性、强度和紧张度等,情绪可以被形式化描述和度量.Barakova利用情感的认知重评策略对交互过程中经验表情进行认知评价,并结合当前情感状态与来自面部表情的情感刺激在唤醒度-效价(Arousal-Valence)情感空间中建立情感状态转移模型,实现在特定的场景中的交互体验[7].Hupont等利用概率统计的方法将离散情感分类器与情感状态空间进行有机的结合,得到用户情感在唤醒度-效价(Arousal-Valence)维度情感空间中的分布,有助于分析情感状态间的相互转移关系[8].该方法依赖多种离散的情感分类器获得训练样本所在的情感空间位置,并且以计算量为代价换取面部特征到多维情感空间投影的准确率.
迄今为止,情感的维度划分方法仍没有统一的定论,比较典型的有二维空间模型(Activation-Evaluation),三维情感模型(pleasure-arousal-dominance, Arousal-Valence-Stance)等[9-11].其中,AVS模型(Arousal-Valence-Stance)结合了外界环境、刺激事件和行为表现,被较好地应用到Kismet机器人中[11].唤醒度A代表情感状态的唤醒程度;效价V代表该情感状态属于哪种类型, 效价值为正说明是积极情感刺激, 反之则为消极情感刺激;姿态S代表某种agent下该刺激的可接受程度.围绕AVS三维情感空间,提出了一种基于个性化认知的情感映射模型,该模型通过结合用户的性格特征,基于GMM构建情感特征与情感维度(情感属性)之间的动态相关性,获得不同情感特征所属的三维情感空间分布,从而实现维度空间中情感的准确映射.该方法的实现并实施,利用已有的底层面部表情特征提取的研究基础[12],采用增量式的GMM模型构建.值得一提的是,随着交互数据的增加,本文所提模型依据个性化交互认知,具有动态地调整GMM模型参数的能力.
1 基于GMM模型的多维情感分析围绕A、V、S三维情感属性,通过基于高斯混合模型使用特征向量的聚类算法构建面部表情情感映射模型.在每一个维度上面部表情特征被分配到聚类,一个聚类对应一个特定的情感,对每种情感聚类分别构建GMM模型N(x|μk, σk), k=1, 2, …, l,AVS三维情感属性的情感分类可由GMM模型表示为Z~(Na, Nv, Ns).从而生成的聚类对应的空间分布划分为l种情感类型Z.={Zi~(Na, Nv, Ns)i}l.
假定视频中获取的一组面部表情特征向量为{X1, X2, …, Xn},对于单一维度m=a, v, s而言,特征向量Xi在第k个高斯分布的后验概率计算如下:
| $ {{p}_{mk}}\left( j=k\left| {{X}_{i}} \right. \right)=\text{ }\frac{{{\pi }_{k}}{{N}_{j}}\left( {{X}_{i}}\left| {{\mu }_{k}}, {{\sigma }_{k}} \right. \right)\text{ }}{\sum\limits_{h=1}^{l}{{{\pi }_{h}}{{N}_{j}}\left( {{X}_{i}}\left| {{\mu }_{h}}, {{\sigma }_{h}} \right. \right)}}.~ $ | (1) |
其中,模型参数πk,μk和σk的大小与微表情的情感空间分布强相关,最大值max(pmk)所指向的情感类型为机器识别出的个体情感状态(显性).为便于计算,令
采用类似的方式拟合出某一情感类型在3种情感属性中的高斯分布.依据高斯分布的“3σ”原则,选取(μ-3σ,μ+3σ)区间作为某类情感状态在坐标轴上的有效分布区间,从而确定情感类型在AVS三维坐标轴上的取值范围.
2 基于增量式的个性化情感映射 2.1 情感的个性化认知由于个体心理认知因素的影响,由情感的复杂性可知个体呈现出的外在情感(显性)往往隐含着多种其他类型的情感状态(隐性).并且在心理认知因素的影响下,各类情感状态之间将会相互制约和转移,最终可能会导致个体真实情感强度甚至情感类型产生变化,如图 1所示.在情感的映射过程中加入个性化认知分析,通过调节个体情感在AVS情感空间中的GMM概率分布,实现对表情情感空间映射结果的实时修正,为获取到具有个性化认知的表情情感分类提供有力支撑.

|
图 1 个体的认知情感转移过程 Figure 1 Transfer process of individual cognitive emotion |
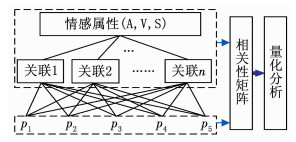
McCraee等运用统计分析方法提出了大五人格理论(Five Factor Model, FFM),是分析个体性格特征的常用心理学量表,包括:外向性(E)、宜人性(A)、尽责性(C)、情绪稳定性(N)、开放性(O).目前, 该理论在机器人情感状态的研究中得到了广泛关注[15].为了研究不同性格特征对个体情感的影响,依据NEO-FFI (Neuroticism Extraversion Openness Five-Factor Inventory)量表评估个体的人格五因素,获得性格特征矢量P =[p1, p2, p3, p4, p5],建立层次分析结构(如图 2所示),包括方案层——性格特征、准则层——人格特征关联和目标层——情感属性.
|
图 2 认知情感的层次分析 Figure 2 Hierarchical analysis of cognitive emotion |
依据实验样本(具体见图 6)的人格五因素数据,采用多元线性回归分析法分别计算个体情感属性与性格特征之间的相关系数,建立相关性矩阵,从而获得个性化认知参数.具体如下:因变量情感属性A, V, S与自变量性格特征P =[p1, p2, p3, p4, p5]之间的线性关系,可表示为
| $ \begin{array}{l} m = \mathit{\boldsymbol{P}}\cdot\mathit{\boldsymbol{\omega }}{_{\rm{m}}} + \varepsilon = \left[{{\rm{ }}{p_1}, {p_2}, \ldots, {p_5}} \right]\cdot\left[\begin{array}{l} {\mathit{\boldsymbol{\omega }}_a}\\ {\mathit{\boldsymbol{\omega }}_v}\\ {\mathit{\boldsymbol{\omega }}_s} \end{array} \right] + \left[\begin{array}{l} {\varepsilon _a}\\ {\varepsilon _v}\\ {\varepsilon _s} \end{array} \right], \\ m = \left[{a, v, s} \right]. \end{array} $ | (2) |
式中:ε为误差,m为个体情感属性值, ωa=[ωai]1×5T, ωv=[ωvi]1×5T, ωs=[ωsi]1×5T为相关性系数矩阵,由最小二乘法对实验样本进行估计获得,使其满足误差的平方和最小,即
| $ {\rm{min}}{\varepsilon ^2} = {\rm{min}}\sum\limits_{j = 1}^n {\left[{m\left( j \right)-\sum\limits_{i = 1}^5 {{p_i}\left( j \right)} \cdot{\omega _{mi}}\left( j \right)} \right].} $ | (3) |
其中n为样本量.依据文献[13]可知,个体性格特征越强,其对情感的认知能力越强;反之,认知能力越弱.由此,规定个体的个性化认知参数为
| $ {\rho _m} = {k_m}\sum\limits_{i = 1}^5 {{p_i}\cdot{\omega _m}}, m = a, v, s. $ | (4) |
其中km为认知强度系数.AVS情感空间中考虑个性化认知后,个体在第k类情感的GMM概率分布为
| $ \begin{array}{l} p{'_k} = {\rm{ }}\left( {p{'_{ak}}, p{'_{vk}}, p{'_{sk}}} \right) = {p_k} + \\ \;\;\;\;\;\;\;\;\;\;\;\left( {{\rho _a}\cdot\Delta {p_{ak}}, {\rho _v}\cdot\Delta {p_{vk}}, {\rho _s}\cdot\Delta {p_{sk}}} \right). \end{array} $ | (5) |
其中,Δpak, Δpvk, Δpsk为个体的情感转移概率值,分别采用有限状态机建立状态转移概率矩阵获得,具体见文献[15].依据式(5),概率越大,表明个体的情感空间位置与该类情感分布越接近.
为了在AVS三维情感空间中实现情感的准确映射,规定高斯概率分布的均值μk=(μak, μvk, μsk)为第k类情感的空间坐标值:ck=μk.以唤醒度(A)情感属性为例,依据式(5)计算个体情感在K个情感类型中的概率值[p'a1, p'a2, …, p'ak],并选取其中概率值较大的两类情感坐标μai和μaj.计算个体在唤醒度坐标轴上的值为
| $ A = {\mu _{ai}} \pm \frac{{{\rm{ }}{p_{aj}}\cdot\left( {{\mu _{aj}}-{\mu _{ai}}} \right)}}{{{p_{ai}} + {p_{aj}}}}. $ | (6) |
类似地,个体情感在效价(V)和姿态(S)坐标轴上的映射值可以被计算出.基于此,依据个体情感与基本情感类型之间的空间相对位置从而判定其所属情感类型.
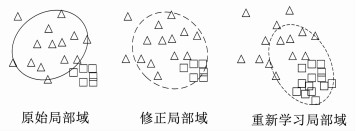
2.2 基于高斯过程回归的增量式学习通过模型的优化计算能够更好地呈现出数据的聚类分布结果.在传统GMM模型算法中通常针对稳定分类器展开的参数计算,常采用EM算法和最小二乘法等优化方法.然而,面部表情所属的情感空间分布依赖于个性化认知的影响,它随着个体用户认知的变化而改变,并且直接影响情感识别的准确度.个性化认知主导下的模型会发生覆盖过多的错分样本,此时这个模型对某类情感映射将会存在较大误差.因此,随着交互历史数据的增加,本文利用增量式学习机制,将情感空间中每个椭球区域作为一个局部域Si,计算历史样本数据在局部域中的权值判断是否需要优化模型参数或重新学习新的模型,从而实现情感映射模型的修正.优化过程如图 3所示.
|
图 3 基于增量式学习的模型优化过程 Figure 3 Model optimization process based on incremental learning |
对于每个历史数据点z=(x:(a, v, s)), 计算局部域Si中各维度(a, v, s)情感分布的高斯核函数为
| $ {w_{ik}} = {\rm{exp}}(-\frac{1}{{2{\sigma _{ik}}^2}}{\left\| {{x_k}-{c_{ik}}} \right\|^2}). $ | (7) |
其中,wik, σik, cik分别为局部域Si中第K维情感分布的权值、方差和中心点.则样本数据在局部域中的权值计算如下:
| $ {w_i} = \frac{{\sum\limits_{k = 1}^3 {{w_{ik}}} }}{{\sum\limits_{i = 1}^l {\sum\limits_{k = 1}^3 {{w_{ik}}} } }}. $ | (8) |
选取最大权值wimax作为判断模型优化学习的依据.设定阈值η,分别对优化模型中可能出现的情况展开分析:1)若样本数据在所属局部域Si内,直接将其作为有效样本存入训练集;2)若样本数据不在所属局部域Si内,权值wimax大于阈值η,则将该样本归为局部域Si并存入训练集,优化模型的参数:中心点、期望和方差;3)样本数据不在所属局部域Si内,权值wimax小于阈值η,则样本存入训练集,并重新学习新模型.
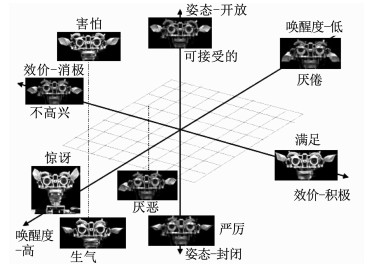
3 实验仿真为了研究个性化认知对情感交互过程产生的影响,展开了针对人格五因素与情感属性两者之间的关联性实验分析.依据Breazeal提出的9类情感状态在AVS空间中的分布情况(如图 4所示)[11],将其进行两种预处理以提升实验的精确性.其一,将每种情感形容词按强度再细分为高、中、低3个等级,共27个情感形容词用于测试者情感的描述;其二,依据情感的空间位置合理量化27种不同情感的三维坐标值,规定各坐标轴的有效区间为[-10, 10].
|
图 4 AVS空间中的情感分布 Figure 4 Emotional distribution in AVS space |
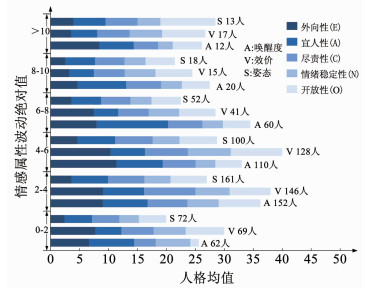
邀请500位参与者,并利用NEO-FFI量表统计他们的人格五因素(如图 5(a)所示),并将测量后每类人格因素的分数规定在区间[0, 10]之内.实验实施过程中,参与者将观看一个20 min短视频(如图 5(b)所示),并利用27个情感形容词描述观影前后的情感状态.选取其中416份有效数据,参照情感的量化坐标进行统计分析,得到参与者情感属性(A、V、S)变化与其人格五因素之间的对应结果如图 6所示.按照观影前后实验者的情感属性波动绝对值进行划分,统计每个情感属性波动区间内所有受试者的人格五因素均值,其中一种色彩条形图代表一类人格因素.例如:唤醒度(A)波动绝对值为[0, 2]的受试者有62人,他们的人格五因素均值分别由5种颜色条状图表示,条状图越长,则其代表的人格均值越大.

|
图 5 用户人格测试与情感跟踪实验 Figure 5 User's personality test and emotion tracking experiment |
|
图 6 情感属性与人格五因素之间的数据统计 Figure 6 Data statistics between emotional attributes and personality five factors |
通过多元线性回归方法对实验数据进行分析,计算出个性化认知参数.由于每种情感属性与人格五因素之间的相关性各不相同,为了保证结果有效性的同时尽可能地简化计算,只保留每种情感属性中相关性较强的3类人格因素.依据实验数据分析结果,人格五因素对情感属性影响的个性化认知参数为
| $ \begin{array}{l} {\rho _a} = 0.22E + 0.35A + 0.19N, {\rm{ }}\\ {\rho _v} = 0.21O + 0.41A + 0.49N, {\rm{ }}\\ {\rho _s} = 0.23O + 0.18N + 0.11C. \end{array} $ | (9) |
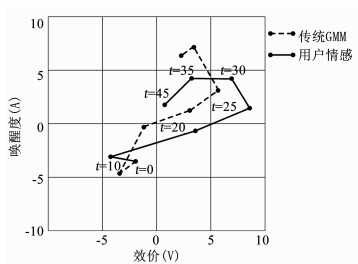
为了直观地评价本文所提算法的有效性和优越性,规定初始情感状态已知,将实验结果与用户的真实情感状态进行比较.一方面邀请用户观看视频片段,持续时间为45 min,并通过27种情感形容词记录该时间段内的各类情感变化;另一方面,以式(9)所述的认知参数作为个性化认知依据,分别使机器人采用传统GMM、具有个性化认知的GMM模型(C-GMM)和本文所提模型(CI-GMM),计算用户在不同时间段的情感状态,并与其真实情感相比较.为了便于观察,通过A-V二维情感空间来呈现实验结果.图 7为在A-V平面中传统GMM模型和用户真实情感状态之间的变化对比,图 8为C-GMM模型和用户真实情感状态之间的变化对比,图 9为CI- GMM模型和用户真实情感状态之间的变化对比.其中采用NEO-FFI量表评估用户的人格五因素,之后依据式(9)获得个性化认知参数为(ρa, ρv, ρs)=(5.76, 8.42, 3.57).
|
图 7 传统GMM情感映射与用户情感对比 Figure 7 Comparison between traditional GMM emotion mapping and user emotion |
|
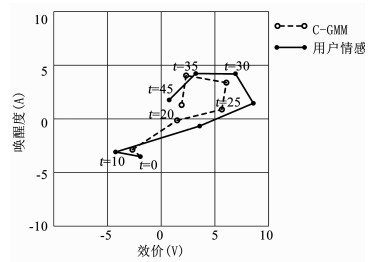
图 8 C-GMM情感映射与用户真实情感对比 Figure 8 Comparison between C-GMM emotion mapping and user emotion |
|
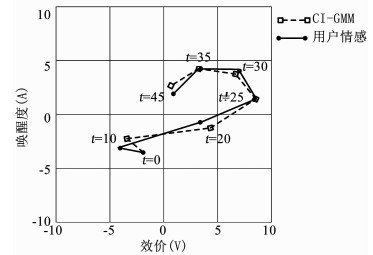
图 9 CI-GMM情感映射与用户真实情感对比 Figure 9 Comparison between CI-GMM emotion mapping and user emotion |
由图 7~9可知,传统GMM算法的情感变化曲线与用户真实情感曲线存在较大的偏差,拟合度偏低;C-GMM算法的曲线拟合度优于传统GMM算法,但由于个体认知的影响,使得情感均倾向于平静状态(中心位置),导致频频出现偏离用户真实情感的现象.而本文所提算法在个性化认知评价的前题下,采用增量式方式对情感分类进行实时调整,使得情感曲线与用户真实情感保持着较高的拟合度.特别地,在t=25 min和t=35 min处,本文算法的效价值和唤醒度值均与真实状态完全一致,保持着较高的准确率.对于传统GMM算法和C-GMM算法:在t=25 min处其与真实状态的唤醒度相近,但效价存在明显差距;在t=35 min处,C-GMM算法的映射结果与用户真实状态相差较小,传统GMM算法与真实状态的效价一致,但唤醒度存在明显的不同步.可见,增量式认知情感映射模型具有较高的情感识别准确率.
参照上述实验,分别计算传统GMM、C-GMM模型和本文所提方法(CI-GMM)对6种基本情感的识别率,经过30组实验后的映射结果如表 1所示.可以看出,本文方法的映射准确率相比其他两种方法都有不同程度的提高.
| 表 1 情感映射结果对比 Table 1 Comparison of emotional mapping results |
提出了一种基于个性化认知的增量式GMM情感映射模型.围绕AVS情感空间的3种属性(A, V, S),采用GMM对空间中的情感类型进行建模,获得情感类型的空间分布.由于个体认知差异性的存在,在情感交互过程中同样的外界输入刺激通常会产生不同的反馈结果.考虑到个性化认知对用户情感理解的影响,本文引入个性化认知参数,分析个体的人格五因素与情感三维属性之间的相关性,并将其结果加入到高斯混合模型,实现具有个性化认知的情感映射模型.为了保证在认知作用下情感映射的准确率,采用基于高斯核函数的增量式学习方法实现了情感映射模型的实时修正.通过与传统GMM模型的实验对比,说明本文所提模型具有较高准确率和有效性.
| [1] |
PENG X L, XIA Z Q, LI L, et al. Towards facial expression recognition in the wild: A new database and deep recognition system[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops. 2016: 93-99.
|
| [2] |
WANG J C, YANG Y H, WANG H M, et al. Modeling the affective content of music with a gaussian mixture model[J]. IEEE Transactions on Affective Computing, 2015, 6(1): 56-68. DOI:10.1109/TAFFC.2015.2397457 |
| [3] |
HERNANDEZ Y, GUSTAVO A F, LUIS E S. A model of affect and learning for intelligent tutors[J]. Journal of Universal Computer Science, 2015, 21(7): 912-934. |
| [4] |
HOSSAIN M S, MUHAMMAD G. Audio-visual emotion recognition using multi-directional regression and ridgelet transform[J]. Journal on Multimodal User Interfaces, 2016, 10(4): 325-333. DOI:10.1007/s12193-015-0207-2 |
| [5] |
MENG H Y, NADIA B B, DENG Y D, et al. Time-delay neural network for continuous emotional dimension prediction from facial expression sequences[J]. IEEE Transactions on Cybernetics, 2016, 46(4): 916-929. DOI:10.1109/TCYB.2015.2418092 |
| [6] |
NICOLAOU M, ZAFEIRIOU S, PANTIC M. Correlated-spaces regression for learning continuous emotion dimensions[C]//21st ACM International Conference on Multimedia, Barcelona, Spain, 2013: 773-776.
|
| [7] |
BARAKOVA E I, GORBUNOV R, RAUTERBERG M. Automatic interpretation of affective facial expressions in the context of interpersonal interaction[J]. IEEE Transactions on Human-Machine Systems, 2015, 45(4): 409-418. DOI:10.1109/THMS.2015.2419259 |
| [8] |
BALDASSARRI S, HUPONT I, ABADIA D, et al. Affective-aware tutoring platform for interactive digital television[J]. Multimedia Tools and Applications, 2015, 74(9): 3183-3206. DOI:10.1007/s11042-013-1779-z |
| [9] |
KAMAROL S K A, JAWARD M H, KALVIAINEN H, et al. Joint facial expression recognition and intensity estimation based on weighted votes of image sequences[J]. Pattern Recognition Letters, 2017, 92(6): 25-32. |
| [10] |
CLARET J A, VENTURE G, BASANEZ L. Exploiting the robot kinematic redundancy for emotion conveyance to humans as a lower priority task[J]. International Journal of Social Robotics, 2017, 9(2): 277-292. DOI:10.1007/s12369-016-0387-2 |
| [11] |
BREAZEAL C. Function meets style: Insights from emotion theory applied to HRI[J]. IEEE Transactions on Systems Man and Cybernetics Part C-Applications and Reviews, 2004, 34(2): 187-194. DOI:10.1109/TSMCC.2004.826270 |
| [12] |
姜波, 解仑, 刘欣, 等. 光流模值估计的微表情捕捉[J]. 浙江大学学报(工学版), 2017, 51(3): 577-583. JIANG B, XIE L, LIU X, et al. Micro-expression spotting using optical flow magnitude estimation[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(3): 577-583. |
| [13] |
SVENSSON C M, BONDOC K G, POHNERT G, et al. Segmentation of clusters by template rotation expectation maximization[J]. Computer Vision and Image Understanding, 2017, 154(1): 64-72. |
| [14] |
HAN M J, LIN C H, SONG K T. Robotic emotional expression generation based on mood transition and personality model[J]. IEEE Transactions on Cybernetics, 2013, 43(4): 1290-1303. DOI:10.1109/TSMCB.2012.2228851 |
| [15] |
MCCRAE RR, COSTA P T. Validation of the five-factor model of personality across instruments and observers[J]. Journal of Personality and Social Psychology, 1987, 51(1): 81-90. |
 2018, Vol. 50
2018, Vol. 50


