桥梁车辆荷载具有高度的随机性,目前仍然难以通过现场测试或数值模拟的方法完全呈现桥梁寿命期(或评估期)内车辆荷载的可变特征,因此,基于极值理论的车辆荷载效应预测成为解决该问题的重要手段.车辆荷载效应极值预测的常用方法[1-2]有:基于经验分布的尾部数据拟合外推、基于穿越次数的Rice公式外推、基于经典极值理论的区组最大值(block maxima, BM)广义极值(generalized extreme value, GEV)外推、基于超阈值(peaks over threshold, POT)的广义帕累托分布(generalized Pareto distribution, GPD)外推,这其中GEV和GPD方法具有坚实的理论基础而应用广泛,但GEV方法要求基础样本满足独立同分布假定,而GPD方法仅要求超阈值样本满足独立同分布假定,且GPD方法相对GEV更能充分利用样本的极值信息.因此,基于POT的GPD方法近年来更多地应用于桥梁车辆荷载效应的极值预测中[3-6].然而,应用GPD进行极值预测的基本前提是:超阈值车辆荷载效应样本满足独立同分布假定(independent identical distribution, IID),这在上述研究中未引起重视.
对于实际随机车流作用下的桥梁车辆荷载效应而言:一方面,受到多种因素的影响往往呈现多峰分布特点[1-2],样本之间不一定满足同分布假定;另一方面,为了获取最不利荷载效应,往往采样间隔较短,使得样本之间具有时间依存关系,不满足独立性假定.因此,直接应用GPD拟合POT数据可能对极值车辆荷载效应产生估计偏差,特别是对于高重现期的荷载效应特征值预测.针对超阈值样本独立性问题,文献[7]提出独立风暴法(method of independent storms, MIS)筛选超阈值样本,MIS方法随后也被各种改进以用于保证超阈值样本的独立性[1, 4].针对同分布假定问题,其他领域的研究表明可以通过划分影响事件的方法将样本进行分类,再应用组合极值模型进行预测[8].最近,组合极值预测方法也开始用于桥梁车辆荷载效应的分析中:文献[9]引入文献[8]基于BM的组合GEV外推方法,将中小跨径桥梁车辆荷载效应按照参与加载货车数量划分加载事件的方法,进行组合极值外推;文献[10]采用组合超阈值样本,在文献[9]的方法基础上针对中小跨径桥梁车辆荷载效应进行组合极值外推.综上,基于事件分类的组合极值预测方法,对于多事件影响下的极值预测很好地解决了IID假定不满足的问题,具有经典极值预测方法更高精度.
文献[9-10]建立了组合极值预测模型的基本框架,但对其中组合模型构建、独立性检验和参数估计等关键问题仍有诸多探讨和改进的地方.本文基于文献[10]组合超阈值方法,提出采用共同阈值改进了组合广义帕累托分布(composite generalized Pareto distribution, CGPD)的极值预测模型,用于受多事件混合影响的桥梁车辆荷载效应(具有时间依存性和多峰分布特性)极值分析.提出了针对CGPD模型的样本独立性检验、阈值选择、参数估计等关键问题的实用解决方法;采用具有精确理论分布的数值算例,验证了改进CGPD模型及其关键解决方法的准确性;最后,阐述了将CGPD方法用于中小跨径和大跨径桥梁的车辆荷载效应极值预测,并对比了CGPD与传统方法在预测极值上的差别.
1 基于POT的改进CGPD预测模型 1.1 GPD基本预测模型假设独立同分布的随机变量序列Xi(i = 1, 2, …, n),其分布函数为F(x),分布函数的上端点为x*.对于某个固定的大值u < x*称为阈值,若Xi>u,则称Xi-u为超出量,其分布函数为
| $ {F_u}\left( x \right) = \Pr \left( {X - u \le x\left| {X > u} \right.} \right) = \frac{{F\left( {x + u} \right) - F\left( u \right)}}{{1 - F\left( u \right)}}. $ | (1) |
经典极值理论中,对于独立同分布随机变量序列,通过区组最大值构建的样本,在样本量趋于无穷大时必然可以采用广义极值分布GEV进行拟合描述[11].同样地,对于超阈值样本,当阈值足够大时,文献[12]指出可以找到超出量的极限分布为广义帕累托分布GPD,即
| $ G\left( x \right) = 1 - {\left( {1 + \xi \frac{{x - u}}{\sigma }} \right)^{ - \frac{1}{\xi }}},x \ge u. $ | (2) |
式中ξ, σ, u分别为GPD的形状参数、尺度参数和位置参数.
GPD拟合超出量POT数据的重要前提是:1)超阈值出现的次数服从泊松分布;2)超阈值的产生满足时间独立性;3)超阈值样本之间满足同分布假定.首先,超阈值的出现本身就是泊松过程,因此满足泊松分布;其次,超阈值样本之间可能存在时间依存性,特别是样本的采样频率很高的情况;最后,超阈值样本同分布假定仍然是目前应用GPD方法预测的重要前提,而组合极值方法能够解决超阈值样本不服从同分布假定的前提,进行极值预测.
1.2 改进CGPD预测模型对于某一随机变量序列Xi(i = 1, 2, …, n),其分布函数为F(x),假定样本之间相互独立,但该序列受到多事件的影响而不满足同分布假定,假设有j(j = 1, 2, ……, m)个事件影响,其中m为最多的可能事件数量.对于给定样本Xi不超过某一分位值x*的概率,可以通过累积概率函数F(x*)计算,而总体样本的累积概率又可以转化为j个事件组合概率的表达,即
| $ P\left( {{X_i} \le {x^ * }} \right) = F\left( {{x^ * }} \right) = \sum\limits_{j = 1}^m {{f_j}} \cdot {F_j}\left( {{x^ * }} \right). $ | (3) |
式中:x*为某一分位值;F(·)为样本的累积概率;Fj(·)为第j个事件的累积概率;fj为第j个事件的组成权重系数.
基于式(3)可以计算超过某一分位值x*的概率为
| $ \begin{array}{l} P\left( {{X_i} > {x^ * }} \right) = 1 - \sum\limits_{j = 1}^m {{F_j}\left( {{x^ * }} \right)} \cdot {f_j} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^m {{f_j}} - \sum\limits_{j = 1}^m {{F_j}\left( {{x^ * }} \right)} \cdot {f_j} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^m {{f_j}} \cdot \left[ {1 - {F_j}\left( {{x^ * }} \right)} \right]. \end{array} $ | (4) |
对任一事件j,设定某一足够大的阈值uj,由于同一加载事件满足独立和同分布假定,根据超阈值定理,可以采用GPD分布拟合超阈值分布,即
| $ \frac{{1 - {F_j}\left( {{x^ * }} \right)}}{{1 - {F_j}\left( {{u_j}} \right)}} = 1 - G\left( {{x^ * };{\xi _j},{u_j},{\sigma _j}} \right). $ | (5) |
式中:G(x*; ξj, σj, uj)为事件j控制下样本分布的超阈值GPD拟合模型;ξj, σj, uj分别为对应的GPD形状参数、尺度参数和位置参数.
结合式(4)、(5),可得
| $ \begin{array}{l} P\left( {{X_i} > {x^ * }} \right) = 1 - F\left( {{x^ * }} \right) = \sum\limits_{j = 1}^m {{f_j}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\left[ {1 - G\left( {{x^ * };{\xi _j},{u_j},{\sigma _j}} \right)} \right] \cdot \left[ {1 - {F_j}\left( {{u_j}} \right)} \right]. \end{array} $ | (6) |
文献[10]给出了上述过程利用组合超阈值样本进行GPD预测,建立了基于GPD的组合极值预测基本框架.事实上,当所有事件都设定相同阈值u时,结合式(6)和式(1)可以确定超出量分布为
| $ \begin{array}{l} {F_u}\left( {{x^ * } - u} \right) = \frac{{F\left( {{x^ * }} \right) - F\left( u \right)}}{{1 - F\left( u \right)}} = \\ \;\;\;\;\frac{{\sum\limits_{j = 1}^m {{f_j}} \cdot G\left( {{x^ * };{\xi _j},{u_j},{\sigma _j}} \right)\left[ {1 - {F_j}\left( u \right)} \right]}}{{1 - F\left( u \right)}}. \end{array} $ | (7) |
如果令gj=fj·[1-Fj(u)]/[1-F(u)],gj的物理含义是:对于相同的阈值u,j事件超阈值样本量占总超阈值样本的权重系数.则式(7)可以转化为
| $ {F_u}\left( {{x^ * } - u} \right) = \sum\limits_{j = 1}^m {{g_j}} \cdot G\left( {{x^ * };{\xi _j},{u_j},{\sigma _j}} \right). $ | (8) |
式(8)可以进一步简化为
| $ {F_u}\left( x \right) = \sum\limits_{j = 1}^m {{g_j}} \cdot G\left( {x;{\xi _j},{u_j},{\sigma _j}} \right). $ | (9) |
说明可以通过j个事件分别确定其超阈值GPD拟合结果,并通过组合概率方法进行极值预测,式(9)还说明可以利用任意合适的尾部逼近函数,通过权重组合方法进行组合极值预测,这极大简化并明确了基于POT的组合极值预测模型基本思路.
对于不同的事件,其最佳阈值选择可能不同,而组合极值外推就需要找到其中共同的阈值,一般选用各个独立事件最佳阈值的最大值.根据超阈值定理,如果某一超出量分布能够用GPD拟合,则比其阈值大的任意位置进行截取仍然满足GPD分布.这样所有事件归于相同的阈值,因此选用各事件中最大阈值作为组合阈值是符合超阈值定理的.
基于上述推导,任意样本的CGPD极值预测方法可以通过图 1所示流程实现,这其中,样本的时间独立性检验、最佳阈值确定及GPD参数估计是CGPD方法应用的关键,这些关键问题在文献[3-7, 10]都有探讨,以下本文给出一种实用解决方法.
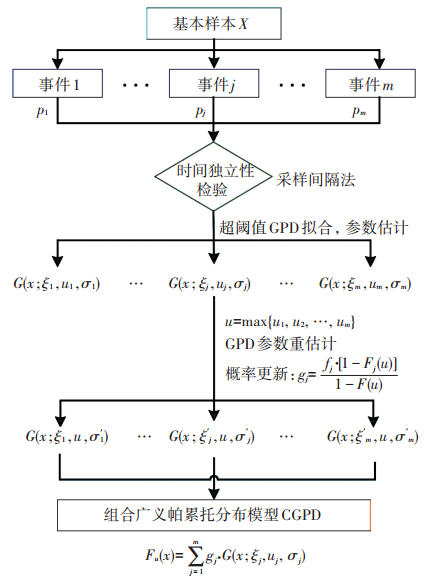
|
图 1 组合广义帕累托分布(CGPD)的极值预测方法及其实施流程 Figure 1 CGPD method and its implementation procedures for extrema prediction |
传统的超阈值理论在设定某一门槛值后,超过门槛值的均选为超阈值POT进行GPD拟合,这使得存在时间依存关系的基础数据在进行POT筛选后样本不能满足独立性假定,从而使GPD拟合结果产生误差.文献[7]提出MIS方法改进阈值的选择,将超阈值连续段作为独立风暴,仅仅选取风暴中的极值作为超阈值,但该方法对于时间依存性强的随机过程样本,仍然无法完全消除超阈值样本的非独立性,例如车辆运行速度较慢时,会出现前后不同风暴极值由同一车队作用产生.
提出一种基于自相关系数的采样间隔法:首先,对样本进行自相关性检验,检验公式为
| $ R\left( j \right) = \frac{{E\left[ {\left( {{X_i} - {\mu _i}} \right)\left( {{X_{i + j}} - {\mu _{i + j}}} \right)} \right]}}{{{\sigma _i} \cdot {\sigma _{i + j}}}}. $ | (10) |
当首次出现R(j)=0时,j就是满足独立性的间隔样本量,如果采样间隔是Δt,则样本满足独立性的时间间隔就是j·Δt;其次,通过峰谷值过滤法进行样本的峰值筛选,例如峰值Xi应该满足Xi≥Xi-1且Xi≥Xi+1,而谷值Xi应该满足Xi≤Xi-1且Xi≤Xi+1;最后,对于给定阈值u,如果超阈值量前后时间间隔小于j·Δt,则筛选其中较大值作为超阈值.
通过上述方法筛选的超阈值满足独立性假定,就能进行GPD分布的参数拟合及极值外推分析.以40 m两车道简支单箱梁桥一侧的支反力在1 d随机车流加载作用下的荷载响应时程为例,如图 2(a),采样间隔1 s,通过荷载响应时程自相关性检验如图 2(b),发现间隔3 s首次出现自相关系数为0,其后自相关系数在0~0.02之间变化,说明数据样本在间隔3 s后满足时间独立性.这也符合实际情况:车辆3 s基本通过40 m跨长的桥梁.
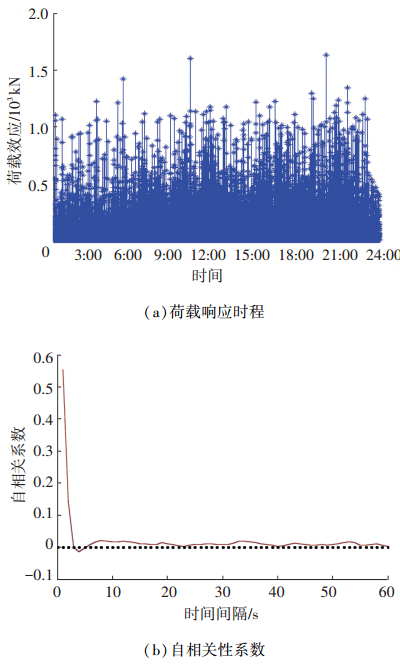
|
图 2 基于自相关系数的采样间隔法进行独立超阈值样本筛选 Figure 2 Selection of independent POT based on autocorrelation coefficient informed sampling interval method |
ξ, σ, u为GPD分布的3个基本参数,其中阈值u的确定至关重要:阈值过高将减少POT样本,使得估计参数的变异性增大;阈值过低可以使参数估计稳定性增强,但会产生有偏估计量.目前针对阈值u选择的方法有图解法和自动计算法,图解法较大依赖于研究者的经验,多是通过定性分析确定阈值的选择.自动计算法则是通过某种算法来计算最小误差或最佳拟合效果的对应阈值,近年来被广泛采用[10-11],提出采用优度拟合中的K-S检验法自动确定最佳阈值.K-S检验法的基本原理是通过拟合数据样本的GPD分布与样本真值进行比较,通过不断改变阈值使得拟合值与真值的比较结果能够满足某种检验门槛,开始满足检验要求的阈值就是最佳阈值.
给定样本X(i =1, 2, …, n)进行顺序排列X(1) < X(2) < … < X(n),可以通过下述步骤寻找最佳阈值:1)确定阈值u=X(i),采用概率权矩法(见2.3节)确定剩余样本GPD分布的参数ξ, σ;2)将参数代入GPD的分布函数中计算为zj(j=i, …, n′);3)将zj与数据样本Xj(j = i, …, n′)的经验累积分布F作K-S检验,满足显著水平5%要求则通过检验;4)如果不满足检验则重新选择阈值u=X(i+1),重复上述过程.根据GPD分布特点,一般可以选择概率密度最大的点作为阈值选择的起始点,以减少迭代次数.采用K-S检验的D值作为检验方法,根据K-S单边检验标准,应该满足D≤Ds,即
| $ D = \mathop {\sup }\limits_{1 \le j \le n} \left| {{z_j} - {F_j}} \right| \le {D_{\rm{s}}} = 1.36/\sqrt n . $ | (11) |
式中F为超阈值样本的经验分布,n为超越阈值的样本量.
图 3给出了两个示例样本基于K-S检验确定的阈值,分别是样本量均为10 000的GPD(0.1, 1, 10)和GEV(0.1, 1, 10)分布.显然GPD分布的样本,其阈值真值为10.0,检验结果验证了K-S方法的正确性;GEV分布的样本,基于K-S检验确定其阈值为10.2,说明对于任意分布形式都可以通过上述K-S优度检验方法确定最佳阈值.
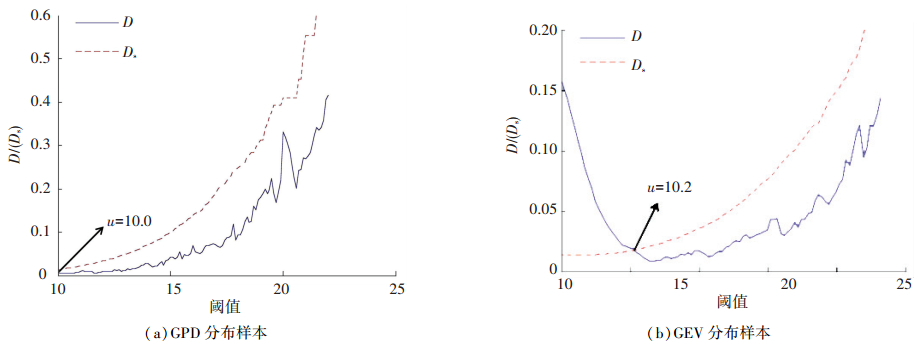
|
图 3 基于K-S优度检验方法的阈值选择算例 Figure 3 Case study of threshold selection based on K-S test |
GPD二参数(形状参数ξ和尺度参数σ)的估计方法众多,有矩法、概率权矩法、线形矩法、极大似然法、贝叶斯估计法[11]等,被用于金融、气候等研究领域.其中概率权矩法改善了矩法估计中高阶样本矩抽样性质不稳定的问题,规避了极大似然法的似然函数难收敛问题,同时也相对贝叶斯估计和线性矩法应用更为简便.本文采用概率权重矩法(probability weight moment method, PWMM)估计GPD分布的形状参数ξ和尺度参数σ.
对于连续性广义帕累托分布的概率权重矩可以定义为[11]
| $ {\omega _{s,r,t}}\left( \theta \right) = E\left[ {{X^s} \cdot {G^r}\left( {X;\theta } \right) \cdot {{\left[ {1 - G\left( {X;\theta } \right)} \right]}^t}} \right]. $ | (12) |
考虑一般的概率权重矩情况,即s=1, t=0,式(12)可以表达为
| $ {\omega _r}\left( \theta \right) = E\left[ {X \cdot {G^r}\left( {X;\theta } \right)} \right]. $ | (13) |
GPD分布需考察样本X的分布参数为θ=ξ, σ,应用GPD分布的前两阶概率权重矩估计.根据式(13),可以计算第r阶概率权重矩为
| $ {\omega _r} = E\left( {X \cdot {G^r}} \right) = \frac{u}{{1 + r}} + \frac{\sigma }{{\left( {1 + r} \right)\left( {1 + r - \xi } \right)}}. $ | (14) |
对于给定的样本,根据式(14)定义样本的r阶概率权矩如下,该定义已被证明是对式(13) ωr的无偏估计[11].
| $ {a_r} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left( {n - i} \right)\left( {n - i + 1} \right) \cdots \left( {n - i - s + 1} \right)}}{{\left( {n - 1} \right)\left( {n - 2} \right) \cdots \left( {n - s} \right)}}{X_{i:n}}} . $ | (15) |
式中Xi:n为初始样本X的顺序排列,即X(1) < X(2) < … < X(i)… < X(n).
根据式(13)、(14),采用前两阶概率权重矩,可以推导GPD两参数分别为
| $ \xi = 1 - \frac{{2{a_1} - u}}{{{a_0} - 2{a_1}}}, $ |
| $ \sigma = \frac{{\left( {2{a_1} - u} \right)\left( {{a_0} - u} \right)}}{{{a_0} - 2{a_1}}}. $ |
概率权重矩法充分利用低阶矩估计样本的GPD参数,且其拟合效果也主要在形状参数ξ < 1之间,特别是在-0.5 < ξ < 0.5时其参数估计的计算效率高且精度好,而桥梁车辆荷载效应的GPD拟合形状参数也基本在上述范围[10-11],因此PWMM法可以很好地用于桥梁车辆荷载效应的GPD拟合中.
3 数值算例验证为了验证CGPD模型及其解决方法的准确性,需要采用具有已知理论分布的样本进行分析.实际的桥梁车辆荷载效应样本往往通过数值拟合方式建立近似的分布函数,难以确定真实的理论分布.这里,构建3个已知分布的数值样本,假定每天样本量为3 000,重复模拟1 000 d,各数值算例的事件组成及其基础分布见表 1.
| 表 1 数值算例的样本参数设置及外推极值比较 Table 1 Parameters of numerical examples and the comparison of extrapolated extrema |
根据样本量3 000及各事件的基础分布,可以计算给定重现期T的外推极值理论值.中国公路桥梁设计规范对车辆荷载及其荷载效应的重现期定义为设计基准期100 a最大值保证率为95%[13],对应于重现期1 950 a:T=1/(1-0.951/100)=1 950,据此数值算例在1 950 a重现期的理论极值见表 1.利用CGPD模型及上述关键方法,进行特征值预测为
| $ {G^{\rm{c}}}\left( {x_T^{\rm{c}}} \right) = 1 - \frac{{{n_d}}}{{365 \times T \times {n_{{\rm{POT}}}}}}. $ | (16) |
式中:c为特征值符号;Gc(·)为CGPD分布函数,通过式(8)计算;xTc为通过CGPD外推的重现期T的特征极值;nt为基础样本的天数;nPOT为nt天内通过CGPD拟合超阈值样本量.
采用Gumbel概率纸呈现各数值算例下各事件的POT数据及其拟合GPD分布和CGPD分布.Gumbel概率纸横坐标为样本,竖坐标采用标准极值变量(standard extreme variate, SEV),通过SEV=-ln(1-F)计算特征值,能更好地呈现尾部极值分布.采用相同阈值比较传统的SGPD方法,观察CGPD和SGPD极值预测的差异.
数值算例1呈现了CGPD极值外推对于预测结果的准确性,其预测1 950 a重现期特征值误差在-3.0%,相比于SGPD具有很好的精度.对比CGPD外推结果与事件1和事件2的关系,可知样本极值在前端是由事件1控制,因此走势与事件1相同;在尾端则由事件2控制,因此尾端走势保持与事件2相同;同样的规律可以在数值算例2和3中发现.采用CGPD方法预测的极值,在数值算例2和3中误差也只有2.1%和2.5%,验证了CGPD方法的合理性和准确性.从CGPD和SGPD的比较来看,3个数值算例均说明:随着预测重现期增大,CGPD方法和SGPD方法预测结果的差异愈加显著,说明采用传统的混合数据进行外推(SGPD),会造成长回归周期下极值的显著高估或低估.比较结果如图 4所示.
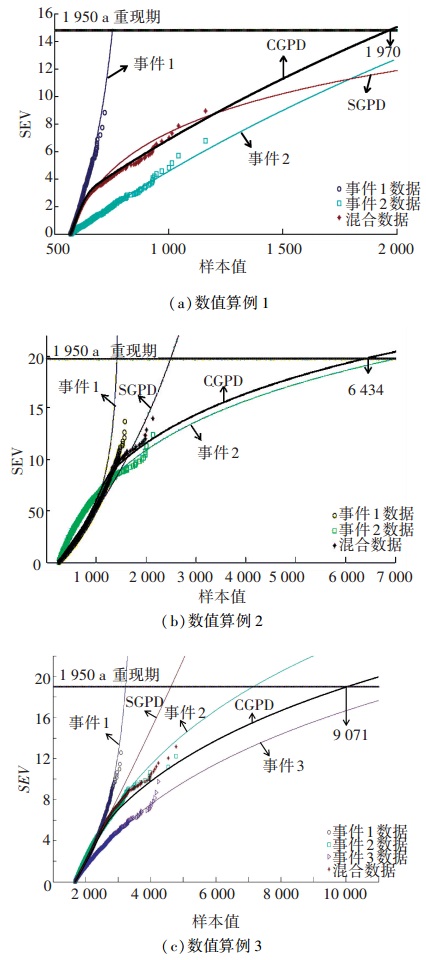
|
图 4 数值算例的CGPD与SGPD极值预测效果比较 Figure 4 Comparison of predicted extrema between CGPD and SGPD for numerical examples |
应用CGPD方法进行桥梁车辆荷载效应的极值预测,这里通过多轴单元胞自动机(multi-axis single-cell cellular automaton, MSCA)[14]模拟车流产生随机车队荷载序列,并加载于桥梁结构效应影响线,获取荷载响应时程.由于中小跨径桥梁与大跨径桥梁的随机车流模拟方法不同,相应的加载控制事件也有显著差异,这里分别针对中小跨径桥梁和大跨径桥梁的随机车流荷载效应采用不同的加载事件分类方法,应用CGPD预测模型,进行1 950 a重现期荷载效应极值预测,该重现期水平是中国公路桥梁车辆荷载的设计标准.注意到,实际桥梁车辆荷载效应的基础分布是未知的,因此没有外推极值的理论解,这里比较CGPD和SGPD方法对实际车辆荷载效应极值估计的差异性.
4.1 中小跨径桥梁车辆荷载效应根据现有研究[9-10],中小跨径桥梁车辆荷载效应可以根据加载货车数量确定加载事件.采用MSCA模拟30 m单向双车道随机车流数据,加载于30 m简支单箱梁桥跨中弯矩的影响线上,计算随机车流荷载效应样本,共模拟3 000 d数据.通过分析该加载事件主要由单辆货车和横向两车道并排行驶两辆货车形成,模拟中观测到非常少量3辆或4辆货车同时加载的情形,由于数据量太小,因此不考虑3辆及其以上货车加载的情形.因而,可以将桥梁车辆荷载效应样本按照两个加载事件(单辆货车和两辆货车)分类,并进行组合极值荷载效应预测.
根据CGPD预测模型和相关方法.首先分别获取各个加载事件及混合加载事件的超阈值样本,并进行时间独立性检验;其次,分别采用优度检验方法选取阈值,并提取各独立事件所选阈值中的最大阈值,采用概率权矩法PPWM进行各加载事件及混合加载事件的GPD参数拟合;再则,采用传统的SGPD方法(忽略加载事件类型)进行外推;最后采用CGPD极值方法通过式(9)外推.所有极值外推考虑设计1 950 a荷载重现期,其计算方法与数值算例相同.
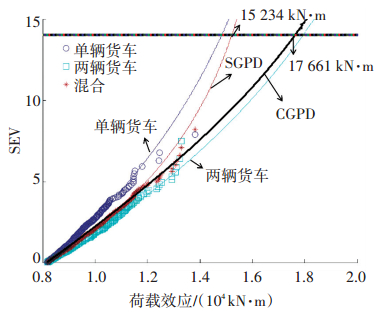
图 5给出了荷载效应CGPD和SGPD预测结果.可以看到:超阈值样本的拟合效果很好,高尾荷载效应主要由两辆货车加载产生,因此CGPD拟合的尾部主要受到两辆货车加载效应的尾部走势决定.从外推特征荷载效应来看,CGPD外推的极值效应(17 661 kN·m)比SGPD外推的极值效应(15 234 kN·m)更大,说明采用传统SGPD外推方法对重现期的极端车辆荷载效应会产生13.7%的预测偏差.
|
图 5 中小跨径桥梁车辆荷载效应的CGPD极值预测 Figure 5 CGPD based extrema prediction of traffic load effects of short and medium span bridges |
选取动态称重(weigh-in-motion, WIM)设备采集的四车道实际通行的车辆荷载数据,日交通流量为33 750 veh/d.WIM数据的日交通流量和重车比率时均参数统计结果如图 6所示.可知交通荷载呈现显著的日夜分布特点:8:00—20:00时段交通流量显著大,高于500 veh/d,货车(≥3.5 t)比率显著低,40%以下,说明虽然该时段交通量大但载重水平低,基本以小轿车为主;其他时段的交通流量显著偏小,但货车比率显著高,特别是0:00—5:00时段货车比重达到近80%.这种日夜差异性,是中国高速公路交通运输的基本现状,同时这也是两种显著差别的交通运营状况与荷载分布.

|
图 6 四车道高速公路实测WIM数据的时均交通流量与时均货车比率变化 Figure 6 Changing rules of the ratio of hourly traffic volume to hourly truck on a four-lane unidirectional highway from measured WIM data |
考虑到大跨径桥梁车辆荷载效应受交通密度和货车比率显著影响,因此上述两个时段构成了正常交通流作用下的典型加载事件,即高时均交通量8:00—20:00时段)和高时均货车比率(0:00—8:00和20:00—24:00时段).注意到,日交通流量33 750较难产生交通拥堵,这里没有考虑因为突发交通事故引起的拥堵问题.模拟1 500 m四车道桥梁在上述交通流特征下的随机车流,重复模拟1 000 d的车流加载作用,以1 500 m跨长四车道范围内的均布荷载集度(单位:kN/m)作为荷载效应,根据CGPD外推方法,获取荷载效应极值,并与SGPD方法预测结果进行比较,拟合分析过程与数值算例相同.
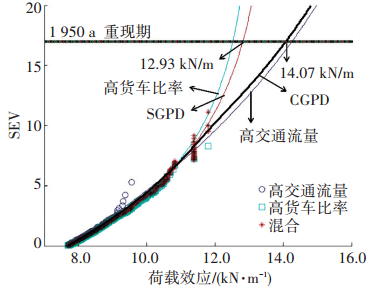
图 7呈现了两种加载事件影响下大跨径桥梁均布荷载集度的尾部GPD拟合及CGPD极值预测效果.可以看到:高时均交通量和高时均货车比率产生的荷载响应尾部都比较长,样本显示“高时均货车比率”对极端值的影响更大,但具有较短的尾部.从外推特征荷载效应来看,CGPD极值外推获得效应(14.07 kN/m)比传统的SGPD极值外推(12.39 kN/m)更大,说明采用传统的SGPD方法对车辆荷载效应极值会产生11.9%的估计误差.
|
图 7 大跨径桥梁车辆荷载效应的CGPD极值预测 Figure 7 CGPD based extrema prediction of traffic load effects of long span bridges |
1) 考虑桥梁车辆荷载效应受到多事件混合影响而不满足同分布假定,提出采用共同阈值改进了CGPD预测模型,能适应采用任意尾部逼近函数预测基于事件分类的超阈值样本的极值.提出基于自相关系数的采样间隔法、基于K-S优度检验的自动计算法和概率权重矩法,用于独立超阈值样本筛选、阈值选取和参数估计.
2) 具有精确理论解的数值算例验证了改进CGPD模型及其关键解决方法的准确性,与理论解的误差在3%以内.传统不区分事件的外推方法,由于忽略了样本不满足独立同分布的前提,相对于CGPD方法在预测高重现期极值上存在很大误差.
3) 中小跨径桥梁荷载效应可以基于参与加载的货车数量划分加载事件,大跨径桥梁荷载效应则可以根据时均交通量和时均货车比率划分时段形成不同加载事件,应用CGPD方法均能方便地获取荷载效应极值,传统方法相对CGPD方法对重现期1 950 a的荷载效应预测误差高达13.7%.
4) 改进的CGPD预测模型及其关键解决方法,也可拓展应用到极端气候和金融风险等极值研究领域,具有广泛推广价值.同时,CGPD相关方法体系对于规范汽车荷载模型的校核与改进,以及特定地点桥梁性能的评估,具有应用价值.
| [1] |
O'BRIEN E J, SCHMIDT F, HAJIALIZADEH D, et al. A review of probabilistic methods of assessment of load effects in bridges[J]. Structural safety, 2015, 53: 44. DOI:10.1016/j.strusafe.2015.01.002 |
| [2] |
阮欣, 周军勇, 石雪飞. 桥梁汽车荷载响应的极值外推方法综述[J]. 同济大学学报(自然科学版), 2015, 43(9): 1339. RUAN Xin, ZHOU Junyong, SHI Xuefei. Review on extreme extrapolation methods for bridge traffic load response[J]. Journal of Tongji University (Natural Science), 2015, 43(9): 1339. DOI:10.11908/j.issn.0253-374x.2015.09.009 |
| [3] |
李植淮, 李春前, 孙健康, 等. 基于GPD模型的车辆荷载效应极值估计[J]. 工程力学, 2012, 29(增刊1): 166. LI Zhihuai, LI Chunqian, SUN Jiankang, et al. Estimation of extreme vehicle load effect based on GPD model[J]. Engineering Mechanics, 2012, 29(Sup1): 166. |
| [4] |
冯海月, 伊廷华, 陈斌. 采用广义Pareto分布进行车辆荷载效应极值估计的研究[J]. 振动与冲击, 2015, 34(15): 7. FENG Haiyue, YI Tinghua, CHEN Bin. Extreme estimation for vehicle load effect based on generalized Pareto distribution[J]. Journal of Vibration and Shock, 2015, 34(15): 7. |
| [5] |
高欣, 王磊. 在役桥梁车辆荷载效应极值概率模型建模方法[J]. 哈尔滨工程大学学报, 2013, 34(8): 995. GAO Xin, WANG Lei. Modelling method for extreme traffic-load effect probabilistic model of an existing bridge[J]. Journal of Harbin Engineering University, 2013, 34(8): 995. |
| [6] |
夏坚, 宗周红, 杨泽刚, 等. 基于GPS的大跨斜拉桥车辆荷载模型[J]. 中国公路学报, 2016, 29(1): 44. XIA Jian, ZONG Zhouhong, YANG Zegang, et al. Vehicle load model of large-span cable-stayed bridge based on GPS[J]. China Journal of Highway and Transport, 2016, 29(1): 44. DOI:10.3969/j.issn.1001-7372.2016.01.006 |
| [7] |
COOK N J. Towards better estimation of extreme winds[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1982, 9(3): 295. DOI:10.1016/0167-6105(82)90021-6 |
| [8] |
GOMES L, VICKERY B J. Extreme wind speeds in mixed wind climates[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1978, 2(4): 331. DOI:10.1016/0167-6105(78)90018-1 |
| [9] |
CAPRANI C C, O'BRIEN E J, MCLACHLAN G J. Characteristic traffic load effects from a mixture of loading events on short to medium span bridges[J]. Structural Safety, 2008, 30(5): 394. DOI:10.1016/j.strusafe.2006.11.006 |
| [10] |
ZHOU X, SCHMIDT F, TOUTLEMONDE F, et al. A mixture peaks over threshold approach for prediction extreme bridge traffic load effects[J]. Probabilistic Engineering Mechanics, 2016, 43: 121. DOI:10.1016/j.probengmech.2015.12.004 |
| [11] |
史道济. 实用极值统计方法[M]. 天津: 天津科学技术出版社, 2006. SHI Daoji. Practical extreme statistical method[M]. Tianjin: Tianjin Science and Technology Press, 2006. |
| [12] |
DAVISON A C, SMITH R L. Models for exceedances over high thresholds[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1990, 52(3): 393. |
| [13] |
中华人民共和国住房和城乡建设部.工程结构可靠度设计统一标准: GB 50153-2008[S].北京: 北京科文图书业信息技术有限公司, 2009 Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Unified standard for reliability design of engineering structures: GB 50153-2008[S]. Beijing: Beijing Science and Technology Library Industry Information Technology Co., Ltd., 2009 |
| [14] |
RUAN X, ZHOU J, TU H, et al. An improved cellular automaton with axis information for microscopic traffic simulation[J]. Transportation Research Part C: Emerging Technologies, 2017, 78: 63. DOI:10.1016/j.trc.2017.02.023 |
 2018, Vol. 50
2018, Vol. 50


