目前中国高速铁路主要采用单一的票价体系.在单一固定的票价下，大部分高速铁路仍处于亏损状态，能力利用处于紧缺与虚糜共存的局面，因此深入研究高速铁路的定价策略对调节客流、提高收益具有重要意义.高速铁路旅客运输具有产品不可存储，有确定的预售期，固定成本高而边际成本低等特点，符合利用收益管理的特征，因此可以将收益管理的动态定价理论运用到高速铁路中，通过适时合理改变车票的价格来调节客流需求、提高收益.

针对收益管理的动态定价理论，国内外学者已经进行了深入研究.文献[1-2]假设需求是连续的时齐泊松过程，研究了单产品和多产品的动态定价问题.文献[3]假设顾客到达为非齐次泊松过程，研究了保留价格随时间变化的动态定价问题.文献[4]研究了需求是价格线性函数条件下的动态定价问题.文献[5-6]研究了需求是泊松过程条件下的连续时间动态定价问题.文献[7]利用马氏纯灭过程对我国铁路实施动态定价进行研究.文献[8]利用Bellman最优化原理探讨了客运专线最优动态票价调整策略.针对需求随机性，部分学者研究了需求不确定下的动态定价模型^[9-11]，并在集装箱班轮运输中得到了一定的应用^[12-13].以上对于动态定价的研究主要侧重于理论研究，在高速铁路旅客运输领域研究较少，并且主要集中在定性研究^[14-16]，对动态定价模型的研究较少.在对我国铁路实施动态定价研究时，通常假设需求是给定强度的非时齐泊松过程^[7-8]，然而在实际工作中，需求强度很难准确预测，因此依据估计出来的需求强度制定票价时，一旦需求估计发生偏差，所制定的票价很可能达不到收益最大化的目的.此外既有文献在考虑需求不确定时，通常是在需求函数的基础上附加随机误差项进行研究^[9]，然而需求函数系数也存在不确定性，并对最优解产生影响.

本文针对需求的不确定性，在考虑需求函数系数波动的条件下，以收益最大化为目标，建立高速铁路动态定价稳健优化模型，并运用稳健优化方法求解，将客票预售期划分为多个售票时段，根据每个时段内各OD客流需求特点为车票制定相应的价格.最后通过具体的案例来验证模型的准确性和稳健性.

1 模型构建 1.1 旅客敏感性分析

旅客市场细分是高速铁路实施动态定价的前提，由于旅客在出行目的、收入、购票时间等属性上存在差异，导致旅客对价格的承受能力不同.对于商务旅客，其收入较高对价格的敏感性相对较低，而对时间的敏感性较高.对于闲暇旅客，通常提前较长时间安排行程，其对价格的敏感性较高，而对时间的敏感性较低^[16].因此可以对我国高速铁路旅客进行细分，利用旅客对价格的敏感性对高速铁路进行动态定价.

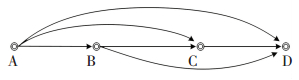
1.2 高速铁路运输组织特点分析

高速铁路列车运输是一个具有多区段，服务多OD需求的复杂网络.如图 1所示为一高速列车的运行线路，列车从A站出发，途径B、C两站，最终到达D站.该列车运行线路上包括A到B，B到C，C到D 3个区段；服务A到B，A到C，A到D，B到C，B到D，C到D间的客流需求.在对高速铁路进行动态定价时，铁路管理部门所能利用的资源就是列车在各区段的席位能力，在不考虑列车超员的情况下，列车在各区段的席位能力相同且等于列车定员，为旅客提供的产品就是各OD上分配的票额.动态定价就是根据各OD旅客在不同售票时段对价格敏感性的不同，来为各OD的车票在不同售票时段制定不同的价格，从而调节各OD客流需求，最终达到高速铁路列车收益最大化的目的.

1.3 动态定价模型构建

设列车n的运行线路上包括m个停站、L个区段，则L=1, 2, ..., m－1；F={(i, j)|i=1, 2, ..., m－1, j=i+1, ..., m}为从i站到j站的OD对集合，其中i、j分别为上车站、下车站序号；将客票预售期划分为T个时段，t为预售期内第t个时段，则t=1, 2, ..., T；l_ij为OD对(i, j)的距离；p_ijt为预售期内第t时段OD对(i, j)的票价，p_ij为OD对(i, j)的票价下限，p_ij为OD对(i, j)的票价上限；C_L为列车在区段L上的席位能力，本文不考虑列车超员，则列车在各区段的席位能力相同，为列车定员C；A_ijL为0-1变量，A_ijL=1为OD对(i, j)占用区段L，否则A_ijL=0.

令x_ijt为客票预售期内第t时段OD对(i, j)的票额需求，根据文献[17-18]中票额需求对价格的反应关系，本文假设票额需求是价格的线性函数，即

$ {x_{ijt}} = {\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}},t = 1,2, \cdots ,T. $

(1)

式中系数α_ijt、β_ijt需要用统计的方法估计出来.然而实际需求可能存在随机波动，并且在对需求函数系数进行估计时，难免会存在估计误差.因此，本文在考虑需求函数系数波动的条件下来构建高速铁路的动态定价稳健模型，以适应需求的这种不确定性，模型M1如下.

1) 目标函数.铁路管理部门通过确定预售期内每个时段各OD的票价及其分配的相应票额，使得铁路部门收益达到最大，即

$ \max z = \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{x_{ijt}} \cdot {p_{ijt}}} } = \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{p_{ijt}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } $

2) 能力约束.占用区段L的所有OD的票额需求之和不能超过列车在该区段的席位能力，不考虑超员情况下，列车在各区段的席位能力等于列车定员，即

$ \begin{array}{*{20}{c}} {\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijt}} \cdot {x_{ijt}}} } \le {C_L},}\\ {\forall t,\;\;\;\;\forall \left( {i,j} \right) \in F,L = 1,2, \cdots ,m - 1.} \end{array} $

3) 票价上下限约束.考虑到铁路运输收益及其铁路的社会公益特性，预售期内每个时段各OD的票价不得低于一个票价下限，同时票价也不能高于一个票价上限，即

$ {\underline p _{ij}} \le {p_{ijt}} \le {{\bar p}_{ij}},\;\;\;\;\;\forall t,\forall \left( {i,j} \right) \in F. $

4) 预售期的同一时段内OD距离越长票价越高，防止动态调整票价时，出现距离短的OD票价高于距离长的OD票价，即

若l_ek>l_ij，则p_ekt>p_ijt,

∀t, ∀(e, k), (i, j)∈F.

5) 预售期的同一时段内票价率服从递远递减规律，即OD票价小于等于组成此OD的各区段的票价之和，即

若Ω={L|(i, j)∈F，且A_ijL=1}，

则${p_{ijt}} \le \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}}} $，∀t.

6) OD的票价应大于组成此OD的各区段的票价之和减去任意区段的票价，即

若Ω={L|(i, j)∈F，且A_ijL=1}，

则${p_{ijt}} > \sum\limits_{L \in \mathit{\Omega }} {{p_{L\left( {L + 1} \right)t}} - {p_{g\left( {g + 1} \right)t}}} $,

∀t，∀g∈Ω.

7) 票价的整数约束，即

$ {p_{ijt}} \in N \cup \left\{ 0 \right\}. $

2 模型求解

在高速铁路动态定价的模型M1中，由于实际需求是随机波动的，因此模型的最优解对需求函数x_ijt(p_ijt)的系数依赖性很强.如果式(1)中系数α_ijt和β_ijt的估计值不准确，那么最优解可能不满足列车席位能力限制的约束，从而不能达到最大化收益的目的.实际上，为了得到稳健最优解，不必要求所有情况的约束条件都必须满足，可以在某个缩小的系数变化范围内求得最优解，它依然能满足适应系数变化的稳定要求，却不至于过多的损失目标函数值.为此，本文引入稳健优化模型方法^{[9-10, 12-13]}，以适应需求的这种不确定性.

令${{\tilde \alpha }_{ijt}} \in [{\alpha _{ijt}} - {{\hat \alpha }_{ijt}},{\alpha _{ijt}} + {{\hat \alpha }_{ijt}}]$，${{\tilde \beta }_{ijt}} \in [{\beta _{ijt}} - {{\hat \beta }_{ijt}},{\beta _{ijt}} + {{\hat \beta }_{ijt}}]$，式中${{\tilde \alpha }_{ijt}}$、${{\tilde \beta }_{ijt}}$为需求函数系数α_ijt、β_ijt的实际值，${{\hat \alpha }_{ijt}} > 0$、${{\hat \beta }_{ijt}} > 0$为系数${{\tilde \alpha }_{ijt}}$、${{\tilde \beta }_{ijt}}$的变化幅度.假设δ_ijt和η_ijt分别是[-1, 1]上取值的变量，δ_ijt为需求函数系数的实际值${{\tilde \alpha }_{ijt}}$与估计值α_ijt之间的偏差程度，η_ijt为需求函数系数的实际值${{\tilde \beta }_{ijt}}$与估计值β_ijt之间的偏差程度，即有${{\tilde \alpha }_{ijt}} = {\alpha _{ijt}} + {{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}}$，${{\tilde \beta }_{ijt}} = {\beta _{ijt}} + {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}}$.第t时段的实际需求量${{\tilde x}_{ijt}} = {{\tilde \alpha }_{ijt}} - {{\tilde \beta }_{ijt}} \cdot {p_{ijt}}$，由此可得，第t时段的实际需求${{\tilde x}_{ijt}}$与名义需求x_ijt相差的绝对值为$\left| {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right|$.

引入参数Γ_ij，Γ_ij为一个非负实数，表示OD对(i, j)客流需求的波动情况，即实际各时段总需求与名义总需求的偏差值，则有

$ \begin{array}{l} \left| {\sum\limits_{t = 1}^T {\left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right)} } \right| \le \\ \sum\limits_{t = 1}^T {\left| {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right|} \le {\mathit{\Gamma }_{ij}}. \end{array} $

Γ_ij值可根据所研究列车各OD的客票销售数据得到，Γ_ij的值越大，表明铁路管理部门掌握的各OD间的需求信息越少，反之，Γ_ij的值越小，则代表铁路管理部门掌握的各OD间的需求信息越多.由此，模型M1可以转化为动态定价稳健模型M2，即

$ \begin{array}{l} \max z = \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{p_{ijt}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } + \\ \min \left( {\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{p_{ijt}} \cdot \left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right)} } } \right). \end{array} $

$ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.:}}\\ \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } + \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot } } \\ \;\;\;\left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right) \le {C_L}, \end{array} $

(2)

$ \sum\limits_{t = 1}^T {\left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right) \le {\mathit{\Gamma }_{ij}}} , $

(3)

$ \begin{array}{l} \sum\limits_{t = 1}^T {\left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right) \le - {\mathit{\Gamma }_{ij}}} ,\\ \left| {{\delta _{ijt}}} \right| \le 1,\left| {{\eta _{ijt}}} \right| \le 1,{\underline p _{ij}} \le {p_{ijt}} \le {{\bar p}_{ij}}, \end{array} $

若l_ek>l_ij，则p_ekt>p_ijt,

Ω={L|(i, j)∈F，且A_ijL=1}，

则${p_{ijt}} \le \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}}} $.

若Ω={L|(i, j)∈F，且A_ijL=1},

则${p_{ijt}} > \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}} - {p_{g\left( {g + 1} \right)t}}} $,

p_ijt∈N∪0.

模型M2中约束条件(3)为$\sum\limits_{t = 1}^T {({{\hat \alpha }_{ijt}}\cdot{\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}})} \le {\mathit{\Gamma }_{ij}}$, 可推导出$\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot ({{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}})} } \le \sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot {\mathit{\Gamma }_{ij}}} $, 由此可以得到${C_L} - \sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot {\mathit{\Gamma }_{ij}}} \le {C_L} - \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}}} } \cdot ({{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}})$, 约束条件(2)为$\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}}} } \cdot ({\alpha _{ijt}} - {\beta _{ijt}}\cdot{p_{ijt}}) \le {C_L} - \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}}} } \cdot ({{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}})$, 将约束条件(2)与约束条件(3)合并，则约束条件(2)可以松弛为$\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}}} } \cdot ({\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}) \le {C_L} - \sum\limits_{\left( {i,j} \right)} {{A_{ijL}}} \cdot {\mathit{\Gamma }_{ij}}$, 由此可以保证约束(2)恒成立.

因此可以进一步将模型M2松弛为下述稳健模型M3，即

$ \begin{array}{l} \max z = \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{p_{ijt}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } + \\ \;\;\;\;\;\;\;\;\;\;\;\min \left( {\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{p_{ijt}} \cdot \left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right)} } } \right). \end{array} $

$ \begin{array}{l} {\rm{s}}{\rm{.t}}{\rm{.:}}\\ \;\;\;\sum\limits_{t = 1}^T {\left( {{{\hat \alpha }_{ijt}} \cdot {\delta _{ijt}} - {{\hat \beta }_{ijt}} \cdot {\eta _{ijt}} \cdot {p_{ijt}}} \right) \ge - {\mathit{\Gamma }_{ij}}} , \end{array} $

(4)

$ \left| {{\delta _{ijt}}} \right| \le 1, $

(5)

$ \left| {{\eta _{ijt}}} \right| \le 1, $

(6)

$ \begin{array}{l} \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } \le {C_L} - \sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot {\mathit{\Gamma }_{ij}}} ,\\ \;\;\;\;{\underline p _{ij}} \le {p_{ijt}} \le {{\bar p}_{ij}}, \end{array} $

若l_ek>l_ij，则p_ekt>p_ijt,

Ω={L|(i, j)∈F，且A_ijL=1},

则${p_{ijt}} \le \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}}} $.

若Ω={L|(i, j)∈F，且A_ijL=1},

则${p_{ijt}} > \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}} - {p_{g\left( {g + 1} \right)t}}} $,

p_ijt∈N∪{0}.

模型M3是一个两层规划问题，其内层规划最小化问题可以看作是以δ_ijt和η_ijt为决策变量的线性规划，约束(4)、(5)、(6)为内层规划的约束条件，求解内层规划的对偶问题，利用强对偶定理可以得到模型M3等价于下述凸规划问题模型M4，即

$ \begin{array}{l} \max z = \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{p_{ijt}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } - \\ \;\;\;\;\left( {\sum\limits_{\left( {i,j} \right)} {{\mathit{\Gamma }_{ij}} \cdot {w_{ij}}} + \sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {\left( {{{\hat \alpha }_{ijt}} - {{\hat \beta }_{ijt}} \cdot {p_{ijt}}} \right) \cdot \left( {{p_{ijt}} - {w_{ij}}} \right)} } } \right).\\ \;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.:}}\\ \;\;\;\;\sum\limits_{t = 1}^T {\sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot \left( {{\alpha _{ijt}} - {\beta _{ijt}} \cdot {p_{ijt}}} \right)} } \le {C_L} - \sum\limits_{\left( {i,j} \right)} {{A_{ijL}} \cdot {\mathit{\Gamma }_{ij}}} ,\\ \;\;\;\;{\underline p _{ij}} \le {p_{ijt}} \le {{\bar p}_{ij}}, \end{array} $

若l_ek>l_ij，则p_ekt>p_ijt,

Ω={L|(i, j)∈F，且A_ijL=1}，

则${p_{ijt}} \le \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}}} $.

若Ω={L|(i, j)∈F，且A_ijL=1}，

则${p_{ijt}} > \sum\limits_{L \in {\bf{\Omega }}} {{p_{L\left( {L + 1} \right)t}} - {p_{g\left( {g + 1} \right)t}}} $,

p_ijt∈N∪{0},

w_ij≥0.

式中w_ij为模型M3内层规划的对偶规划中的决策变量.

求解模型M4，即可得到客票预售期内每个时段每个OD的最优定价.

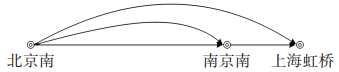
3 案例分析 3.1 动态定价分析

以京沪高速铁路列车G1的二等座车厢为例，G1的运行线路上包括3个客运站2个区段，如图 2所示. G1列车的二等座车厢定员为871人，即C_L= C=871，根据文献[19]中的规定，目前票价可以上下浮动10%，则各OD票价及其上下限见表 1，各OD距离大小关系为：南京南到上海虹桥之间的距离小于北京南到南京南之间的距离，北京南到南京南之间的距离小于北京南到上海虹桥之间的距离.

根据具体研究情况可以将客票预售期划分为若干时段，本文以3个时段为例进行研究，即t取值为1、2、3，t越小表示越接近列车发车时间，即第1时段为离发车时间最近的时段.根据收益管理思想可知，需求函数系数α_ijt随t增大而减小，β_ijt随t增大而增加，表示越临近发车时间，旅客需求对价格的敏感性越低^[10]，α_ijt和β_ijt的变化幅度${{\hat \alpha }_{ijt}}$和${{\hat \beta }_{ijt}}$随t增大而增加，表示越临近发车时间需求估计越准确^[11].即在售票初期(t取3时)由于人们不能确定出行时间所以需求量较小，因此售票初期α_ijt值较小，需求估计偏差${{\hat \beta }_{ijt}}$较大，而此时旅客对价格的敏感性较高，因此售票初期β_ijt和${{\hat \beta }_{ijt}}$较大，可以通过降低票价来吸引客流.

以2015年7月20日—2015年7月26日G1次列车的二等座客票数据为基础，根据收益管理思想给出不同售票时段各OD需求函数系数估计值及其变化幅度，如表 2所示.各OD需求波动值Γ_ij可根据每天各OD的客票销售量与各OD平均每天客票销售量相差的绝对值，然后再取均值得到，Γ_ij值见表 2.

如果铁路管理部门在售票过程中，不考虑旅客对价格的敏感性，在每个售票时段都采用单一全价票方式进行客票销售，则根据表 2中不同售票时段的需求函数关系，利用式(1)计算全价票下各OD的客票需求如表 3所示.

根据表 3中单一全价票下的各OD客流需求，利用文献[20]中的票额分配模型，以收益最大化为目标，得到的票额分配结果如表 4所示.从表 4的票额分配结果可以看出，表 3中各OD的客流需求都得到了满足，说明列车席位能力比较充足.

铁路管理部门在考虑不同售票时段旅客对价格的敏感性时，利用Lingo12.0对本文所构建模型M4进行求解，得到不同售票时段各OD最优定价，并利用式(1)求出不同时段各OD所分配的票额，结果如表 5所示.

由表 5的结果可以看出，运用收益管理理论，在考虑旅客对价格的敏感性时，本文所构建的动态定价模型可以根据不同售票时段需求的特点为车票制定最优价格，根据表 5中各OD的收益，可以求得本文方案所获得总收益为392 008元.与表 4对比，可以看出，虽然利用动态定价方案所实现的客流总需求并没有得到很大的提高，但是结合表 3可以看出，动态定价方案通过动态调整不同售票时段车票的价格，使得各OD不同售票时段所分配的票额发生了变化，即动态定价方案可以在合适的时间将合适的车票销售给最合适的旅客，对客流需求具有一定的调节作用.根据表 4中各OD的收益，可以计算得到单一全价票下获得的总收益为374 258元.因此本文方案所获得的收益较目前单一全价票销售获得的收益有所提高.由此说明，本文提出的基于收益管理的高速铁路动态定价模型较目前单一票价模型更优.

3.2 模型稳健性分析

本文称不考虑需求波动的模型为名义模型.相比名义模型，所构建动态定价稳健模型具有更高的鲁棒性，对需求波动的适应性更强，下面通过仿真模拟来分析名义模型和稳健模型所得到的最优解打破列车席位能力约束的概率.在不考虑需求波动时，利用Lingo 12.0求解模型M1可以得到确定需求下各OD在各时段最优定价，如表 6所示.

根据表 5、6中不确定需求和确定需求的动态定价决策及其表 2中各系数的取值，假设δ_ijt、η_ijt都为[-1, 1]均匀分布的随机变量，利用MATLAB进行编程，通过10 000次模拟计算来验证模型的稳健性，模拟结果表明：在稳健模型下约束被打破的概率为28.55%，在名义模型下约束被打破的概率为56.14%.

根据模拟结果可知：在名义模型下票额需求超过列车席位能力的概率达到56.14%，而稳健模型中票额需求超过列车席位能力的概率为28.55%，由此可以看出稳健模型得到的最优解能够更好地适应需求的波动.此外，由于名义模型得到的最优解打破约束条件的概率较大，因此在将其作为动态定价策略时，会在客票销售初期将客票销售完，而早期到来的旅客通常是愿意为车票付低价的旅客，这就使得铁路管理部门失去了在客票销售后期以更高价格销售车票而获利的机会.对于稳健模型，其打破能力约束的概率相比名义模型较小，这就使得利用稳健模型最优解作为动态定价策略时，铁路管理部门可以有更多的机会在客票销售后期以更高的价格售出车票，从而获得更多的收益.因此，稳健模型不仅可以适应需求的波动而且可以使铁路管理部门有更多的机会将车票销售给愿意付更高价格的旅客.

4 结论

1) 在分析高速铁路不同售票时段旅客对价格敏感性和高速铁路运输组织特点的前提下，利用收益管理理论研究了需求函数系数不确定的高速铁路分时段动态定价稳健模型，并利用稳健优化方法进行求解，最后以京沪高铁列车为例验证了高速铁路采用收益管理理论进行动态定价时，相比目前单一的定价策略，不仅可以调节客流需求而且可以提高铁路运输收益.

2) 利用稳健优化模型得到的动态定价决策不仅可以适应需求的波动而且可以保证铁路管理部门将更多的车票以更高的价格销售，从而保证获得更多的收益.

3) 模型仅仅研究了单列车的情况，此外，需求函数系数及其变化幅度和客流需求的波动情况需要在长期的运输实践过程中不断积累完善，今后将进一步研究多列车及其高铁运输网络的动态定价模型.