2. 哈尔滨工业大学 交通科学与工程学院,哈尔滨 150090
2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China
刚性路面结构参数反演是刚性路面结构性能评价、结构补强设计以及有限元参数标定的关键技术之一.刚性路面结构参数反演的方法主要有3种,逐点拟合法[1]、最优化求解法[2-7]和衍生指标法[8-15].衍生指标法通过变量的分步求解简化了参数反演的计算过程,物理意义明确,与其他两类方法相比,具有计算简单快速、实用性强等特点,满足工程级应用要求,在公路、机场刚性路面结构参数反演的工程实践中多采用这类方法[8, 15-16],代表性方法有弯沉盆面积指数法[8-11],惰性弯沉点法[12-13]和弯沉盆重心指标法[14].
弯沉盆面积指数法通过构造弯沉盆面积指数进行刚性路面结构参数解析解的估算,其数学意义在于利用变量分离实现复杂函数组的反函数的数值计算,以分步求解结构参数;与弯沉盆面积指数法的原理相似,弯沉盆重心距离法则充分利用了各测点的弯沉盆信息构造新的衍生指标,并以理论与实测弯沉盆误差最小为原则分步反算结构参数;惰性弯沉点法则根据弯沉盆中存在的唯一惰性点,利用该点具有不随板的弹性模量变化而变化的特性,简化参数反演的计算过程.然而,由于各衍生指标反演方法均包含复杂数学函数的运算[8],采用衍生指标法确定结构参数变量的取值往往需要指定的专业软件(如ILLI-BACK等),对专业技术的要求较高,在工程实践中不简单方便、可操作性不强,而额外的软件费用在一定程度上限制了方法的规模化推广应用;再者,多数工程技术人员对参数反演的本质未进行系统研究,不能科学掌握各衍生指标参数反演方法的特性及其应用边界,这可能降低刚性路面结构参数反演结果的准确性和可靠性.
因此,综合量化分析代表性弯沉盆衍生指标的特性,科学简化刚性路面结构参数反演方法业已成为当前路面运营管理、维修养护等亟待解决的问题.本文系统梳理3类弯沉盆衍生指标参数反演方法的原理和计算模型,采用MATLAB编写相应的结构参数反演程序,通过数值分析的方法综合分析3类衍生指标的规律特性,提出3种方法实用的计算图表或简单的回归关系模型.以典型刚性路面结构形式为例,分析3类衍生指标法的准确性和鲁棒性,探讨其工程适用的有效性及可操作性.
1 地基模型与挠度解析解 1.1 地基模型水泥混凝土面层下的地基通常采用两种假设[17],其一是以地基反应模量K表征地基刚度的Winkler地基假定(K地基);其二是以弹性模量E和泊松比μ表征地基刚度的弹性半空间地基假定(E地基).对刚性路面,美国AASHTO力学经验设计指南(mechanistic empirical pavement design guide,MEPDG)[18]在Winkler地基模型推导的解析解的基础上,建议采用CBR值、地基反应模量等参数进行刚性路面板荷载应力与环境应力的分析.陈荣生等采用薄板有限元法分析了Winkler地基和弹性半空间地基的结构响应,发现Winkler地基模型可更好地反映了板下地基的实际工作状态[19];丹佛机场的现场测试结果表明弹性半空间地基模型计算的地基支撑强度偏高,且容易产生奇异点[20].因此,本文采用Winkler地基板的小挠度薄板力学模型对荷载作用下刚性路面结构响应进行分析,如图 1所示,地基上任一点的反力仅与该点的挠度成正比,而与其他点无关.

|
图 1 Winkler地基模型 Figure 1 The Winkler foundation model |
Winkler地基模型假定地基表面压力与其竖向位移成正比,记K为地基反应模量,则q=Kω.在轴对称垂直荷载作用下,通过积分变换法求解Winkler地基上无限大板的弹性曲面微分方程,板挠度为
| $ \omega \left( r \right) = \frac{1}{K}\int_0^\infty {\frac{{\bar p\left( \xi \right){J_0}\left( {\xi r} \right)\xi }}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi } . $ | (1) |
式中:ω(r)为距荷载重心r处的挠度值,即弯沉值,m;q为ω(r)为地基表面压力;K为板下地基反应模量;ξ为积分变量;J0为0阶贝塞尔函数;p(ξ)为零阶汉克尔变换式;l为板和地基的相对刚度半径,m,计算公式为
| $ l = {\left( {\frac{{E{h^3}}}{{12\left( {1 - {\mu ^2}} \right)K}}} \right)^{\frac{1}{4}}}. $ | (2) |
式中:E为板的弹性模量,Pa;μ为板的泊松比;h为板的厚度,m.
当板表面的受力为半径a的圆形均布荷载p时,零阶汉克尔变换式为
| $ \omega \left( r \right) = \frac{{pa}}{K}\int_0^\infty {\frac{{{J_0}\left( {\xi r} \right){J_1}\left( {\xi a} \right)}}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi } . $ | (3) |
式中:p为荷载集度,N/m2;a为承载板的半径,m;J1为1阶贝塞尔函数.
2 弯沉盆衍生指标利用落锤式弯沉仪FWD采集的弯沉盆数据,刚性路面结构参数的反演是根据式(3)计算得到板的弹性模量E和基层的地基反应模量K.根据式(3),弯沉值ω(r)与变量E、K的关系包含复杂的无穷积分计算,是复杂的多维非线性函数关系,采用理论解析的方法直接反算结构参数E、K十分复杂和困难.在保证准确性的同时,为提高参数反算的效率,许多学者研究并提出了刚性路面弯沉盆的衍生指标及其相应的反演方法.
2.1 弯沉盆面积指数(AREA)Ioannides等[8]发现板的挠度是初等函数
| $ {A_w} = \left( {\sum\limits_{i = 0}^{n - 1} {{A_i}} } \right)/\omega = \sum\limits_{i = 0}^{n - 1} {\left( {{\omega _i} + {\omega _{i + 1}}} \right){s_i}/\left( {2{\omega _z}} \right)} . $ | (4) |
式中:A为指定断面的面积,si为测点i与测点i+1之间的距离,ωi为测点i的挠度,ωz为指定距离处的挠度值,n为测点的数量,各参数的物理意义如图 2所示.

|
图 2 弯沉盆面积指数计算示意图 Figure 2 Definition of deflection basin area |
文献[8]通过数值分析证明了Aw和l存在单调递增的非线性关系,在结构参数反演时,首先通过匹配相同断面面积下实测弯沉盆面积指数Awm和理论弯沉盆面积指数Awt以推算相对刚度半径l,进而根据式(2)、(3),反算地基反应模量K和板的弹性模量E分别为
| $ K = \frac{{pa}}{{{\omega _z}}}\int_0^\infty {\frac{{{J_0}\left( {\xi r} \right){J_1}\left( {\xi a} \right)}}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi } , $ | (5) |
| $ E = \frac{{12\left( {1 - {\mu ^2}} \right)K{l^4}}}{{{h^3}}}. $ | (6) |
孙立军等[12-13]发现对刚性路面弯沉盆,在其他物理量取值不变的情况下,不同板弹性模量E对应的弯沉盆曲线相交于一个狭小的区域,该狭小区域可用某个点来替代,所造成的误差不超过3%,这个点被称之为“惰性点”,如图 3所示.文献[12]通过数值分析后认为“惰性点”存在且具有唯一性,即惰性点与地基反应模量K存在一一对应关系,可解决两层刚性路面结构的逆分解不唯一的问题.基于惰性点的结构参数反演包含两个步骤:1)根据“惰性点”距离荷载中心位置和弯沉值大小,先计算得到地基反应模量K;2)匹配指定测点弯沉值,采用式(2)、(3)计算板的弹性模量E.

|
图 3 不同板弹性模量下弯沉盆惰性弯沉点示意 Figure 3 Inertial point of deflection basin with different slab thickness |
由于弯沉盆面积指数法仅利用了指定测点的弯沉值,没有充分利用其他测点的弯沉信息,导致反演结果受测量误差影响大且具有多解性等问题[11, 15].当板的弹性模量和地基反应模量的数值之比一定(即相对刚度半径l确定)时,对相同距离区间所围成的弯沉盆,其重心与荷载中心的距离为定值,如图 4所示.在此基础上,构建了一种新的弯沉盆衍生指标:弯沉盆重心距离指标[14],即
| $ {d_{CG}} = \frac{{\int_0^d {rd\left( r \right){\rm{d}}r} }}{{\int_0^d {d\left( r \right){\rm{d}}r} }} = \frac{{\int_0^d {r\left[ {\int_0^\infty {\frac{{{J_0}\left( {\xi r} \right){J_1}\left( {\xi a} \right)}}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi } } \right]{\rm{d}}r} }}{{\int_0^d {\left[ {\int_0^\infty {\frac{{{J_0}\left( {\xi r} \right){J_1}\left( {\xi a} \right)}}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi } } \right]{\rm{d}}r} }}. $ | (7) |

|
图 4 刚性路面弯沉盆重心距离示意 Figure 4 Barycentric horizontal distance of deflection basin |
文献[14]通过数值分析表明,弯沉盆的重心距离指标与相对刚度半径之间呈单调递增的关系.在结构参数反演时,先通过匹配实测弯沉盆重心距离和理论弯沉盆重心距离以推算相对刚度半径l,在此基础上,以理论弯沉值和实测弯沉值的误差最小化为原则,根据式(3),反算的地基反应模量K如式(8)所示,进而采用式(2)反算板的弹性模量E.
| $ K = \frac{{\sum\limits_{i = 0}^{n - 1} {{{\left( {pa\int_0^\infty {\frac{{{J_0}\left( {\xi {r_i}} \right){J_1}\left( {\xi a} \right)}}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi } } \right)}^2}} }}{{\sum\limits_{i = 0}^{n - 1} {\left( {pa\int_0^\infty {\frac{{{J_0}\left( {\xi {r_i}} \right){J_1}\left( {\xi a} \right)}}{{1 + {l^4}{\xi ^4}}}{\rm{d}}\xi \cdot {d_i}} } \right)} }}. $ | (8) |
采用MATLAB编写Winkler地基模型和刚性路面弯沉盆的衍生指标,根据式(3)、(4)、(7),采用数值分析方法计算理论惰性点、理论弯沉盆面积指数和理论弯沉盆重心距离.衍生指标计算的模型参数取值如下:1)相对刚度半径l作为连接板的弹性模量E和地基反应模量K的“桥梁”,在参数反演的计算过程中,若l取值区间太小,可能导致搜索不到全局最优的l值;但若l取值区间过大,也将导致计算空间的膨胀而大幅降低计算效率.同理,l取值步长过大,可能错过全局最优的l值,而l取值步长过小,将导致反演计算的效率降低.根据实际工程中弯沉盆的情况以及多次反复试算的结果,研究l取值在[0.5, 2],步长为0.01. 2)结构参数的反演过程等价于从挠度的多次正算过程中选择离目标值最接近的一组参数组合,在理论上需要多次计算式(3)的无穷积分.为提高反演的计算效率,需是预先确定积分上限.经过多次试算的结果,积分上限取20可满足反演的精度要求.
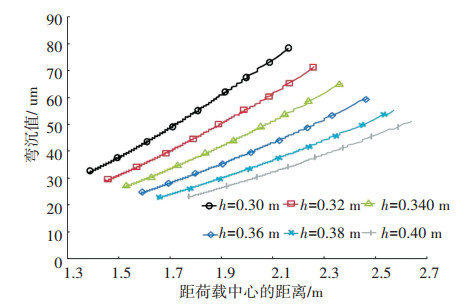
3.2 惰性点与惰性曲线以36 cm厚度的路面为例,不同地基反应模量下的惰性点分布如图 5所示.每一个地基反应模量下都对应着一个唯一的惰性点(红色点),且随着地基反应模量K的增加,惰性点至荷载中心的距离减少,相应的弯沉值的减小.将不同地基反应模量下的惰性点连接起来,将形成一条“惰性曲线”.该曲线性,随着至荷载中心距离的增加,弯沉值呈单调递增.不同路面厚度下惰性曲线族的分布如图 6所示.刚性路面的“惰性曲线族”具有相互不交叉的特征,这证实了惰性点存在的唯一性.随着板的厚度增加,惰性曲线向远离中心的方向偏移,即对同一弯沉盆,如果路面的板越厚,则地基反应模量越小,这与实际情况相符.

|
图 5 不同地基反应模量下的惰性点分布 Figure 5 Inertial point with different foundation reaction modulus |
|
图 6 不同路面厚度下的惰性曲线分布 Figure 6 Inertial curve with different pavement sab thickness |
不同相对刚度半径下弯沉盆面积指数的分布如图 7所示.弯沉盆面积指数随相对刚度半径的增加而严格地单调递增,这证实了通过匹配理论与实测的弯沉盆面积指数反算相对刚度半径是可行且唯一的.当相对刚度半径取值为0.5~2.0 m时,弯沉盆面积指数在0.70~1.35之间变化,增长的幅度随相对刚度半径的增加逐渐平缓.

|
图 7 弯沉盆面积指数与相对刚度半径的关系分布 Figure 7 Distribution between Aw and l |
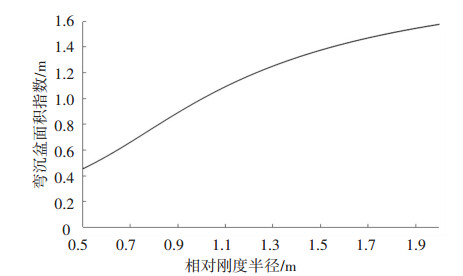
不同相对刚度半径下弯沉盆重心距离的分布如图 8所示.弯沉盆重心距离随相对刚度半径的增加而严格地单调递增,通过匹配理论和实测的弯沉盆重心距离反算相对刚度半径是可行且唯一的.当相对刚度半径取值为0.5~2.0 m时,重心距离在0.4~1.6间变化.与弯沉盆面积指数相比,重心距离随相对刚度半径的变化趋势更为陡急,呈持续增长态势.
|
图 8 弯沉盆重心距离与相对刚度半径的关系 Figure 8 Distribution between dCG and l |
分析式(4)、(7)可以发现,弯沉盆面积指数和重心距离的理论解析式是l的复杂非线性无穷积分函数,直接进行计算将十分复杂和耗时.根据大量理论数值计算的结果,提取弯沉盆面积指数、弯沉盆重心距离与相对刚度半径l的有效样本,采用SPSS软件的非线性回归分析两个衍生指标与l的关联关系.从公式的简单和实用性出发,基于试算数据,得到弯沉盆面积指数、弯沉盆重心距离与相对刚度半径的m次方的关系,见表 1.
| 表 1 弯沉盆面积指数、弯沉盆重心距离与相对刚度半径m次方的判定系数(R2) Table 1 Determination coefficients (R2) among of Aw, dCG and lm |
由表 1可见,弯沉盆面积指数、弯沉盆重心距离与l采用5次幂函数的多项式相关时,判定系数已达到最高值,因此,两个衍生指标与相对刚度半径的关系可以统一表示为
| $ y = {a_1}{l^5} + {a_2}{l^4} + {a_3}{l^3} + {a_4}{l^2} + {a_5}l + {a_6}. $ | (9) |
对相关数据进行回归分析,得到预估模型的待定回归系数,见表 2.模型拟合度R2均为1,五次曲线能很好的模拟弯沉盆面积指数、重心距离随相对刚度半径的分布状况.
| 表 2 弯沉盆面积指数与弯沉盆重心距离与相对刚度半径的多项式回归系数 Table 2 Polynomial regression coefficients among of Aw, dCG and l |
弯沉盆面积指数Aw和弯沉盆重心距离dCG的关系模型分别如式(10)、(11)所示.在已经实测弯盆值的情况下,可采用图 7、8的图解法,或是式(10)、(11)的关系模型,计算相对刚度半径,进而根据式(5)、(6)反演结构参数.与理论解析解的复杂积分函数相比,五次曲线到时候具有简单、实用的工程适用性.
| $ \begin{array}{l} {A_w} = 0.041\;9{l^5} - 0.370\;2{l^4} + 1.362\;9{l^3} - \\ \;\;\;\;\;\;\;\;2.693\;9{l^2} + 3.0267\;l - 0.253\;9,{R^2} = 1. \end{array} $ | (10) |
| $ \begin{array}{l} {d_{CG}} = - 0.304\;6{l^5} + 2.184\;1{l^4} - 5.994\;5{l^3} + \\ \;\;\;\;\;\;\;\;7.435\;8{l^2} - 3.085\;5l + 0.759\;2,{R^2} = 1. \end{array} $ | (11) |
为验证3类衍生指标法及其关系模型的效用,采用数值模拟实验的方法,在不同实验条件下对比分析结构参数的真值和参数反演的估计值,考察参数反演结果的准确性和鲁棒性.
4.1.1 实验算例采用机场典型的刚性路面结构为例,结构参数取值如下:水泥混凝土板厚度为0.4 m,板弹性模量为38 GPa,泊松比为0.15,地基反应模量为100 MN/m3,0.3 m直径的圆形均布荷载(140 kN).根据式(2),相对刚度半径l的真值为1.2 m.弯沉盆衍生指标由路面结构参数和测点传感器共同决定,根据规范要求[16],FWD设备传感器的间距取0.3 m,且取距离荷载中心1.5 m范围内的弯沉盆.根据式(1),距中心距离0、0.3、0.6、0.9、1.2、1.5 m的测点理论弯沉值分别120、115、104、90、76、63 μm.
4.1.2 FWD弯沉数据模拟当前国内外主流FWD设备在刚性路面采集弯沉的误差包括系统误差(±2%)和随机误差(±2 um)[15],实测弯沉值与理论弯沉值的通用关系可表示为
| $ {w_m} = {w_t} + 0.02{w_t}\frac{{\left( {{r_1} - 0.5} \right)}}{{\left| {{r_1} - 0.5} \right|}}{r_2} + 2\frac{{\left( {{r_3} - 0.5} \right)}}{{\left| {{r_3} - 0.5} \right|}}{r_4}. $ | (12) |
式中:wm为FWD误差作用下实测弯沉值,wt为弯沉理论真值,r1、r2、r3、r4是在[0, 1]的随机数.根据实验算例中每一测点的真实挠度值与式(12),对每一测点随机植入弯沉误差,采用实验模拟生成100组实测弯沉盆,每组弯沉盆6个测点的平均绝对误差分布如图 9所示.

|
图 9 6个测点挠度的平均绝对误差分布 Figure 9 Average absolute error of sensored deflection |
对每一组模拟的实测弯沉盆,对惰性点法,在已经板厚度的条件下,可采用图解法绘制实测弯沉盆与图 6中惰性曲线族的交点,该交点对应的地基反应模量值即为结构参数反演值;进而,通过匹配实测弯沉盆中某个测点的弯沉值计算板的回弹模量.对弯沉盆面积指数法和弯沉盆重心距离法,根据3.4节中衍生指标与相对刚度半径的关系模型,计算实测弯沉盆对应的相对刚度半径l,进而根据2.1节和2.3节的反演原理,逐步反演结构参数K和E.
4.2 反演结果分析 4.2.1 准确性分析100组模拟实测沉盆的参数反演的实验统计结果见表 3,与惰性点法和面积指数法相比,重心距离法的MAPE分别提升了10%和5%左右.整体而言,在随机误差的作用下,弯沉盆重心距离法的反演参数的准确性最高,反演的结构参数几乎等于真值,而弯沉盆面积指数其次,惰性弯沉点最差.同时,弯沉盆重心距离法明显减小了其标准差而提高了信噪比,这表明其参数反演结果随误差的波动性最小,参数反演的结果更为可靠, 分析如下:
| 表 3 3种衍生指标法参数反演的统计结果 Table 3 Comparison of back-calculation results of three methods |
“惰性点”法虽然简化了反演计算,但由于惰性点不是一个物理意义上的点而是一个狭小的区域,因此该方法反演的结果隐含固有误差;另一方面,FWD采集的弯沉盆相邻测点的间距较大,相邻弯沉点进行插值处理将成倍增加反演结果的计算误差,致使该参数反演方法的误差波动最为显著,稳定性差.
与惰性点法相比,面积指数法使用指定测点的弯沉信息回避理论插值的误差,明显使反演参数更趋近于真值,反演结果更为稳定,但由于没有综合地利用其他测点的信息,反演的变量K只能保证指定测点处理论与实测弯沉值相等,在其他测点弯沉值误差的综合作用下,参数反演的结果存在多解性,这在很大程度上制约了该方法的准确性和可靠性.
与惰性点法和面积指数法相比,重心距离法综合利用各测点的弯沉信息,对相对刚度半径更为敏感性(图 7),能快速准确地捕捉到相对刚度半径的变化,在解决反演结果多解性的同时,以理论与实测弯沉值的误差最小为原则反算结构参数,显著提高模型拟合精度和减小反演参数的差异,使得参数反演结果的准确性和可靠性均得到大幅提高(反演误差均小于5%).
4.2.2 鲁棒性分析3种衍生指标法在随机测量误差作用下反演统计结果见表 3.其相对误差的绝对值分布如图 10所示.整体而言,3种方法反演的结构参数均在“真值”内外震荡,重心距离法随测点摄入误差的震荡幅度和变化频率最小,面积指数法次之,惰性弯沉点的最大.综合3个衍生指标来看,惰性点法和面积指数法反演结果的相对误差分布与摄入误差的变化规律较一致,虽然弯沉盆重心距离法的反演结果与摄入误差间没有统一的关系,但其反演误差一直保持最小且波动最为平缓,与惰性点法和面积指数法相比,稳定性提高均达35%以上,这表明重心距离法对各测点不同误差的敏感性低,系统具有更强的鲁棒性.

|
图 10 结构参数(l, K, E)反演值的精度随测点摄入误差的变化特性 Figure 10 Accuracy of back-calculated parameters with different field deflection error |
1) 系统构建了刚性路面结构参数反演中弯沉盆面积指数法、惰性点法和弯沉盆重心距离法的计算模型体系,解析其参数反演的原理和计算步骤.采用理论数值计算分析的方法,综合分析3类衍生指标法的分布规律特性.
2) 弯沉盆面积指数、重心距离与相对刚度半径均呈严格的单调递调关系,重心距离随相对刚度半径的增长更为陡峭,二者均可采用五次曲线精确拟合其与相对刚度半径的相互作用关系.
3) 惰性点法将狭小区域看成点,且弯沉盆相邻两测点之间线性插值造成反演结果随摄入误差的波动最为显著;弯沉盆面积指数法完全依懒于中心测点的弯沉值而忽略其他测点使得准确性和鲁棒性较差;弯沉盆重心距离法综合利用各测点信息并使拟合误差最小化,适用于更高精度路面结构性能评价的应用.
4) 衍生指标回归关系模型的拟合精度高,可直接适用于图解法和模型公式法,或是生成参数反演的相应知识库,与专业工具或复杂积分函数相比,这是一种简单易用、极具工程可操作性的有效近似方法,该简化的模型和图表仍需在实践中进一步现场检验.
| [1] |
DARTER M I, HALL K T, KUO C M. Support under Portland cement concrete pavements: NCHRP 372[R]. Washington DC: National Academy Press, 1995
|
| [2] |
HARICHANDRAN R S, MAHMOOD T, RAAB A R, et al. Modified Newton algorithm for backcalculation of pavement layer properties[J]. Transportation Research Record: Journal of the Transportation Research Board, 1993, 1384: 15. |
| [3] |
GOPALAKRISHNAN K. Neural network—swarm intelligence hybrid nonlinear optimization algorithm for pavement moduli back-calculation[J]. Journal of Transportation Engineering, 2009, 136(6): 528. DOI:10.1061/(ASCE)TE.1943-5436.0000128 |
| [4] |
AMIN S R, AMADOR-JIMÉNEZ L E. Backpropagation neural network to estimate pavement performance: dealing with measurement errors[J]. Road Materials and Pavement Design, 2017, 18(5): 1218. DOI:10.1080/14680629.2016.1202129 |
| [5] |
SHARMA S, DAS A. Backcalculation of pavement layer moduli from falling weight deflectometer data using an artificial neural network[J]. Canadian Journal of Civil Engineering, 2008, 35(1): 57. DOI:10.1139/L07-083 |
| [6] |
REDDY M A, REDDY K S, PANDEY B B. Selection of genetic algorithm parameters for backcalculation of pavement moduli[J]. International Journal of Pavement Engineering, 2004, 5(2): 81. DOI:10.1080/10298430412331309106 |
| [7] |
查旭东, 王秉纲. 基于同伦方法的路面模量反算研究[J]. 中国公路学报, 2003, 16(1): 1. ZHA Xudong, WANG Binggang. Backcalculation of modulus for pavements based on homotopy method[J]. China Journal of Highway and Transport, 2003, 16(1): 1. DOI:10.3321/j.issn:1001-7372.2003.01.001 |
| [8] |
IOANNIDES A M. Dimensional analysis in NDT rigid pavement evaluation[J]. Journal of Transportation Engineering, 1990, 116(1): 23. DOI:10.1061/(ASCE)0733-947X(1990)116:1(23) |
| [9] |
SHUO L, FWA T F, TAN K H. Closed-form back-calculation of rigid-pavement parameters[J]. Journal of Transportation Engineering, 1996, 122(1): 5. DOI:10.1061/(ASCE)0733-947X(1996)122:1(5) |
| [10] |
FWA T F, CHANDRASEGARAN S. Regression model for back-calculation of rigid-pavement properties[J]. Journal of Transportation Engineering, 2001, 127(4): 353. DOI:10.1061/(ASCE)0733-947X(2001)127:4(353) |
| [11] |
程国勇, 雷亚伟, 黄旭栋. 基于HWD测试的弯沉盆面积指数法及改进[J]. 中国民航大学学报, 2016, 34(1): 32. CHENG Guoyong, LEI Yawei, HUANG Xudong. Deflection basin area index method and improvement based on HWD test[J]. Journal of Civil Aviation University of China, 2016, 34(1): 32. DOI:10.3969/j.issn.1674-5590.2016.01.008 |
| [12] |
孙立军, 胡圣, 张小宁. 路面弯沉盆上的惰性点[J]. 公路交通科技, 2001, 18(3): 1. SUN Lijun, HU Sheng, ZHANG Xiaoning. Inertial point on deflection basin of concrete pavement and asphalt pavement[J]. Journal of Highway and Transportation Research and Development, 2001, 18(3): 1. DOI:10.3969/j.issn.1002-0268.2001.3.001 |
| [13] |
朱洁, 孙立军. 沥青路面三层结构模量反演最佳反演点的确定[J]. 同济大学学报(自然科学版), 2017, 45(2): 203. ZHU Jie, SUN Lijun. Determination of optimal backcalaulation point for three layer structure modulus backcaluation of asphalt pavement[J]. Journal of Tongji University (Natural Science), 2017, 45(2): 203. DOI:10.11908/j.issn.0253-374x.2017.02.007 |
| [14] |
LIU S F, LING J M, YANG W C, et al. Closed-form back-calculation of rigid-pavement parameters using barycentric horizontal distance of deflection basin[C]// Compendiumof the 96th Transportation Annual Meeting.Washington DC: Transportation Research Board, 2017
|
| [15] |
林小平, 袁捷, 凌建明, 等. 刚性路面弯沉盆面积指数反演改进方法[J]. 中国公路学报, 2009, 22(3): 14. LIN Xiaoping, YUAN Jie, LING Jianming, et al. Improved deflection basin area parameters back calculation method for rigid pavement[J]. China Journal of Highway and Transport, 2009, 22(3): 14. DOI:10.3321/j.issn:1001-7372.2009.03.003 |
| [16] |
凌建明, 张光辉, 刁永海, 等.民用机场道面评价技术管理规范: MH/T 5024—2009[S].北京: 中国民用航空局, 2009 LING Jianming, ZHANG Guanghui, DIAO Yonghai, et al. Technical specifications of aerodrome pavement evaluation and management: MH/T 5024—2009[S]. Beijing: Civil Aviation Administration of China, 2009 |
| [17] |
孙立军. 铺面工程学[M]. 上海: 同济大学出版社, 2012: 195. SUN Lijun. Pavement engineering[M]. Shanghai: Tongji University Press, 2012: 195. |
| [18] |
Applied Research Associates. Guide for mechnistic-empirical design of new and rehabilitated pavement structure: NCHRP project 1-37A[R]. Washington DC: Transportation Research Board, 2004
|
| [19] |
陈荣生, 唐伯明, 秦家宽. 刚性路面板下两种地基模型的对比研究[J]. 中国公路学报, 1990, 3(2): 1. CHEN Rongsheng, TANG Boming, QIN Jiakuan. Comparative study of two kinds of foundation model under rigid pavementslab[J]. China Journal of Highway and Transport, 1990, 3(2): 1. |
| [20] |
RUFINO D, ROESLER J, BARENBERG E. Mechanistic analysis of pavement responses from Denver International Airport: COE Report 26[R]. Rosemont: FAA Center of Excellence (COE) for Airport Technology, 2004
|
 2018, Vol. 50
2018, Vol. 50


