粗粒土通常被传统的冻胀研究认定为冻胀不敏感性材料[1],加上其具有强透水性、高压实性、高抗剪强度以及不易液化等良好的工程特性,因此通常被用作建筑工程土基填料.然而,根据季节性粗粒冻土地区公路、铁路和机场等工程的实际反馈,粗粒土地基冻胀问题仍然时有发生,尤其是局部地基出现的不均匀冻胀变形所造成的危害已不容忽视.青藏高原果洛机场砂砾土冻胀率室内试验[2]和哈尔滨—大连高速铁路路基粗颗粒填料冻胀量监测[3]等研究结果表明,粗粒土基层在一定的温度、含水率、压实度和含泥量(直径小于0.075 mm的颗粒的质量分数)等因素的组合下也会产生一定程度的冻胀病害,尤其是当土基层中的含水率和含泥量分布不均匀时,所产生的不均匀冻胀现象将导致更大的危害[4].因此,充分了解粗粒土地基道面结构不均匀冻胀的原因和机理,为不均匀冻胀病害的防治提供理论依据和建议措施是很有意义的.
粗粒土冻胀问题已经受到了许多学者的关注[5-8],然而关于不均匀冻胀的研究则相对较少.文献[9]通过试验观测、理论分析和相应计算,获得了水泥混凝土路面、沥青混凝土路面容许不均匀冻胀值.文献[10]分析认为道路产生不均匀冻胀的主要原因有土质、压实度和水分的供给,并给出了防治建议.文献[11]研究了某公路路面纵向裂缝和不均匀冻胀的关系.文献[12]通过试验验证了不均匀冻胀在土基边缘沉降和中心隆起现象中的作用.文献[13]分析认为季节性冻土地区的光伏支架基础严重遭受不均匀冻胀的危害,并给出了建议措施.
综上粗粒土冻胀和不均匀冻胀的研究现状,大部分研究集中于公路和铁路路基等方面,关于机场道基的研究较少;且多数研究往往粗略地从整体冻胀的角度进行研究,关于不均匀冻胀的研究较少且研究成果相对零散,而将粗粒土冻胀和不均匀冻胀二者结合的研究更少,难以为砂砾土地基道面结构不均匀冻胀的防治提供有价值的建议.因此,本文拟采用室内模型试验与数值模拟相结合的方法进行研究,结合果洛机场工程实际,以果洛机场采用的道面结构方案为原型,自主设计了道面结构不均匀冻胀模型试验箱,开展了外部水分入渗道肩和道面结构不均匀冻胀模型试验,然后以模型试验为原型,建立相应的水热力三场耦合数值模型,通过模型试验有限测点和有限断面的数据来验证数值模型的可靠性,然后利用数值模拟全面性的优势,更加客观全面地揭示道面结构内部温度场、水分场和冻胀量的基本规律,充分了解砂砾土地基道面结构不均匀冻胀的原因和机理,为道面结构不均匀冻胀病害的防治提供有效的理论依据.
1 室内模型试验 1.1 工程背景果洛机场位于青藏高原季节性砂砾冻土地区,该地区年平均气温为-4 ℃、雨(雪)水充沛、负温期长达8个月以上、当地最大冻深达2.5米[3];该地区的土层结构主要包括下层的天然砂砾土和表层的细粒土,容易造成土基不均匀冻胀;地下水位很低,因此试验中忽略地下水补充对冻胀的影响;果洛机场采用传统道面结构,其示意图如图 1所示.
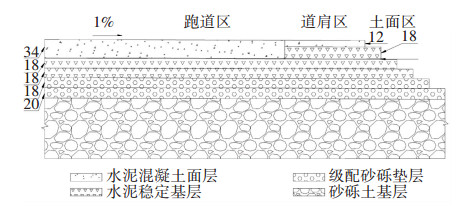
|
图 1 传统道面结构示意图 Figure 1 Diagram of traditional pavement structure |
本文只讨论跑道与道肩之间的冻胀错台,而不考虑各跑道面板之间的冻胀错台.跑道与道肩冻胀错台和道面结构形式及施工方法密切相关,在传统的道面结构中,道肩面层薄于跑道面层,且后于跑道面层施工,跑道面层施工养护用水和雨水产生的径流都流向道肩区,由于道肩区外侧土面区高于道肩基层,因此部分积水无法顺利排出,从而积聚在道肩区并入渗土基层,导致道肩下土基的含水率(本文“含水率”均指体积含水率)大于跑道下土基的含水率,最终导致跑道与道肩产生冻胀错台,其过程示意如图 2所示.
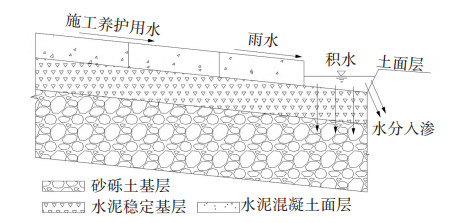
|
图 2 外部水分入渗示意图 Figure 2 Diagram of external water infiltration |
为了确定砂砾土基层的含泥量和质量含水率的实际水平,从而为设置试验条件提供参考,进行了实测调查并得到结果见表 1.可以看出,各抽样点的含泥量水平相差比较大,反映了表层细粒土不均匀地分布在天然砂砾土中,各点的含水率分布规律不明显,尚需进一步研究.
| 表 1 实测含泥质量分数和含水率 Table 1 Silt content and water content |
对天然砂砾土和表层细粒土进行颗粒分析试验,相应的颗粒级配曲线如图 3所示.可见,天然砂砾土中的粗颗粒含量较多,而细颗粒含量相对较少,表层细粒土的土粒粒径小于1 mm[14].砂砾土的不均匀系数(47)和曲率系数(2.1)均大于细粒土的不均匀系数(25)和曲率系数(1.4),说明了前者的粒径级配和冻胀不敏感性较后者更加良好但是前者过大的不均匀系数却反映出了其缺乏中间颗粒,而表层细粒土在土基层施工过程中容易被不均匀地混掺在天然砂砾土当中,在一定程度上填补了天然砂砾土所缺失的中间颗粒,增大了土基层的平均含泥量,增强了砂砾土地基的冻胀敏感性.

|
图 3 颗粒级配曲线 Figure 3 The grading curve |
本文自主设计和加工了道面结构不均匀冻胀模型试验装置,其主要组成部分包括试验箱、计算机测控系统、环境箱、降温控制系统、18B20型数字式温度传感器、FDR-100型频域反射式水分传感器、位移传感器、温度采集卡、水分采集卡、位移采集卡,其中试验箱是以传统道面结构为原型,按照10:1的比例自主设计和加工的,箱体材料为有机玻璃,其示意图和实物图分别如图 4、5所示.为了突出主要因素,简化次要因素,将级配砂砾垫层视作砂砾土基层.由于实际道面结构没有下方边界条件约束,所以在设计模型试验箱的时候,为了减小下部边界约束影响,使模型更加贴近实际情况,将道面结构模型总的厚度增加至36 cm,试验箱高度取为38 cm.环境箱以大型冰柜为基础,配备降温控制系统,最低温度可降低至-20 ℃,可以自动调节降温速率.
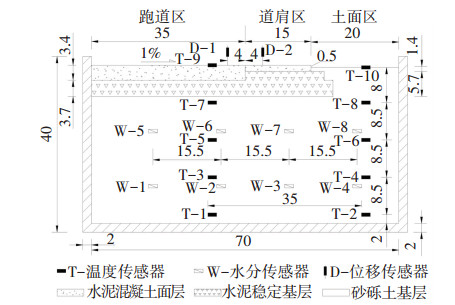
|
图 4 试验箱示意图(cm) Figure 4 Schematic of the test chamber (cm) |

|
图 5 试验箱实物图 Figure 5 Test chamber and model body |
试验所用土样取自果洛机场现场试验段,包括天然砂砾土和表层细粒土.考虑到采用原状土样开展室内试验存在诸多困难,本文所有室内试验均采用重塑扰动土样[15].结合表 1实测数据,在室内模型试验中,含泥量(质量分数)取为10%,初始含水率(质量分数)取为7%.由图 3可知,天然砂砾土的含泥量为6.9%,表层细粒土的含泥量为50%,根据计算所得比例和加水量,将这两种土样按比例掺合均匀、然后均匀喷洒所加的水,焖料24 h,即可得到试验所需的含泥量为10%、初始含水率为7%土样.
1.5 试验步骤1) 对所有水分传感器进行率定,绘制各自的率定曲线.将加工好的试验箱放置于平整坚实的地面,按照95%的压实度、土基空间的体积以及砂砾土试样的密度称取一定质量的试样,以5 cm的层高分层夯实,在填土的同时按照图 4所示的位置布置温度传感器T-1~T-10和水分传感器W-1~W-8,并将它们与计算机连接.按照图 4所示的位置和尺寸浇筑水泥稳定基层和水泥混凝土面层并且在标准养护条件下养护7 d,所有结构层向土面区方向倾斜1%的坡度.在道面面层表面与有机玻璃箱壁交界处用玻璃胶密封,防止边缘渗水.
2) 将2.7 kg水分为3次并间隔一段时间均匀洒向道面结构表面.待所洒水分全部充分入渗完毕,观察水分传感器读数变化,持续到水分读数变化不大时,将此时的水分分布记为冻结初始水分场.在试验箱底面及四周包裹8 cm厚的保温材料并密封严实,然后放入环境箱,按照图 4所示的位置布置位移传感器D-1和D-2.
3) 开启降温控制系统,将初始冻结温度设置为4 ℃,对试验箱整体进行预降温处理,观测温度传感器读数,当T-9和T-10的读数降到4 ℃左右时,将冻结温度设置成以0.1 ℃/h的速率下降,开始冻结,同时打开计算机测控系统,自动记录并保存水分传感器、温度传感器和位移传感的实时监测数据.
4) 当T-3和T-4的读数刚降为0 ℃以下、而T-1和T-2的读数仍然在0 ℃以上时,说明此时冻结线降到H=25 cm附近,关闭环境箱电源和降温控制系统.当所有读数均回升至正温且保持一段时间后,拆除水泥混凝土面层和水泥稳定基层,分别沿跑道区中心方向(X=29.5 cm)、道肩区中心方向(X=45 cm)和土面区中心方向(X=60.5 cm),按照深度分别为9、14、21、28、35 cm取点实测含水率.
5) 整理和分析试验结果.
2 数值模拟 2.1 基本方程1) 基本假定.为保证数值模拟计算的可行性,突出主要因素,忽略次要因素,特作出如下假设:a)土体均匀连续分布,且为各向同性弹性体;b)冰晶体与土粒刚度充分大;c)未冻土与冻结土都认为是弹性体,其值与水分、温度有关;d)忽略水分的气相迁移,只考虑水分的液态迁移;e)不考虑土体中盐分的影响;f)达西定律适用于水分迁移[16].
2) 温度场基本方程.本文不考虑冻融过程中水汽蒸发耗热、质量迁移、化学势和溶质势等作用,只考虑冰水相变、介质水和土骨架的热传导作用,砂砾冻土温度场的基本方程为[16]
| $ \bar C\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right) + L{\rho _{\rm{w}}}\frac{{\partial {\theta _{\rm{w}}}}}{{\partial t}}, $ | (1) |
温度初始条件为
| $ T\left| {_{t - 0}} \right. = {T_0}, $ | (2) |
温度边界条件为
| $ T\left| {_s} \right. = {T_{\rm{b}}}. $ | (3) |
式中:C=ρC+Lρw∂θu/∂T为等效体积比热容,ρ为介质的密度,C为介质的质量比热容,L为水相变潜热,ρw为水的密度,θu为未冻水体积,T为温度,t为时间,λ为介质的导热系数,θw为总含水率,T0为初始温度,s为边界,Tb为边界温度.
3) 水分场基本方程.文献[16]指出饱和水或非饱和水的多孔均匀介质的水分场基本方程均为
| $ \frac{{\partial {\theta _{\rm{w}}}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {k\frac{{\partial \psi }}{{\partial x}}} \right) + \frac{\partial }{{\partial {\rm{y}}}}\left( {k\frac{{\partial \psi }}{{\partial y}}} \right) - \frac{{\partial k\left( \theta \right)}}{{\partial y}}. $ | (4) |
式中:k导水系数,ψ为土水势,k(θ)为土体的渗透系数.
4) 应力场基本方程.通过对各个冻胀因素的分析和计算,考虑降温对土体变形的影响,同时考虑冰水相变和水分迁移对体积应变的影响,得到冻土体积应变计算公式为
| $ {\varepsilon _v} = {\varepsilon _{vT}} + {\varepsilon _{vf}}, $ | (5) |
式中:εv为总的应变,εvT为温度变化导致的体积应变,εvf为冰水相变导致的体积应变.将εv看作初始应变,则土体单元的应力-应变关系为
| $ \left\{ \sigma \right\} = \left[ {\rm{D}} \right]\left( {\left\{ \varepsilon \right\} - \left\{ {{\varepsilon _0}} \right\}} \right), $ | (6) |
其中:[D]为弹性矩阵,
联立式(1)、(4)、(5)即为冻土区水分、温度、应力的耦合基本模型.为了便于求解,引入阶梯函数对该三场耦合模型进行简化.
未冻水和负温之间存在一个函数关系,当温度很低时,土体当中仍然存在未冻水,这些未冻水随温度变化而产生的相变作用即使在相当低的温度范围内仍然会发生.为了使计算简便,本文假定冰水相变发生的温度范围为(Ti-Td, Ti),其中Ti为冻结初始的温度,当土体的温度大于Ti时为融土,当土体的温度小于Ti-Td时为冻土[16].土体冻结过程中水分场、温度场、应力场三场之间互相影响,形成动态耦合作用,在动态耦合作用下的三场物理参数很难在数值计算当中客观表达出来.为了能有效地求解,本文采用Heaviside阶梯函数对同一表达土体水热力三场物理参数,建立砂砾土冻胀水热力三场耦合模型[16].
阶梯函数H(T, d)的表达式为
| $ H = \left\{ \begin{array}{l} 1,\;\;\;T \ge d;\\ \frac{{3T}}{{4d}} - \frac{{{T^3}}}{{4{d^3}}} + \frac{1}{2},\\ 0,\;\;\;\;\;T \le - d. \end{array} \right.\;\;\;\;\; - d < T < d; $ | (7) |
式中:d为一个比较小的正数,T为温度,H在区间(-d,d)内是一个三次函数,从0平滑过渡到1,一阶导数连续,具有更好的光滑性.
在整个土层内部温度与未冻水的体积含量的关系可以等效表示为
| $ \begin{array}{l} {\theta _u} = a{\left| T \right|^{ - b}}\left( {1 - H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right)} \right) + \\ \;\;\;\;\;\;{\theta _0}H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right), \end{array} $ | (8) |
综合导水系数可以等效表示为
| $ \begin{array}{l} k = {k_0}{{\rm{e}}^{dT}}\left( {1 - H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right)} \right) + \\ \;\;\;\;\;\;{k_0}H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right). \end{array} $ | (9) |
综合导热系数可以等效表示为
| $ \lambda = {\lambda _{\rm{f}}} + \left( {{\lambda _{\rm{u}}} - {\lambda _{\rm{f}}}} \right)H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right). $ | (10) |
综合体积比热容可以等效表示为
| $ C = {C_{\rm{f}}} + \left( {{C_{\rm{u}}} - {C_{\rm{f}}}} \right)H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right). $ | (11) |
综合弹性模量可以等效表示为
| $ E = {E_{\rm{f}}} + \left( {{E_{\rm{u}}} - {E_{\rm{f}}}} \right)H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right). $ | (12) |
综合泊松比可以等效表示为
| $ \upsilon = {\upsilon _{\rm{f}}} + \left( {{\upsilon _{\rm{u}}} - {\upsilon _{\rm{f}}}} \right)H\left( {T - {T_i} + \frac{{{T_d}}}{2},\frac{{{T_d}}}{2}} \right). $ | (13) |
式中:k0为未冻水导水系数, υu为融土的泊松比,υf为冻土的泊松比,λu为融土的导热系数,λf为冻土的导热系数,Eu为融土的弹性模量,Ef为冻土的弹性模量,Cu为融土的质量比热容,Cf为冻土的质量比热容.
关于土水势的描述方法比较多,目前尚未统一,其中文献[17-18]所提出的分凝势SP的概念,能够比较好地描述土水势与温度的关系,具体表示式为
| $ q = SP \cdot \nabla T. $ | (14) |
结合水分迁移公式,可以得出土水势和温度之间的关系为
| $ \psi = \frac{{SP}}{{k\left( \theta \right)}} \cdot T + {\psi _0}. $ | (15) |
式中:k(θ)为土体的渗透系数,饱和情况下为常数,本文初始含水率非常接近饱和含水率,故k(θ)可近似取作常数.则式(15)可以等效为
| $ \psi = m \cdot T. $ | (16) |
式中m为试验系数,根据不同土体,取值不同.
2.3 有限元模型建立及参数选取 2.3.1 有限元建模本文采用大型通用商业有限元软件ABAQUS进行数值模拟,由于该软件并没有内嵌水热力三场耦合模型,因此本文对其进行了专门的二次开发.为了验证道面结构不均匀冻胀模型试验,同时检验数值模拟的精度及其在道面结构不均匀冻胀问题研究中的正确性和适用性,以模型试验箱为原型同时参考实际工程环境建立有限元模型如图 6所示,模型总长70 cm、宽20 cm、高38 cm,分为混凝土结构层(上方绿色区域),水泥稳定层(中间红色区域)和砂砾土层(下方灰色区域).

|
图 6 有限元模型 Figure 6 Finite element model |
1) 初始条件.砂砾土层初始温度取9 ℃,初始含水率取19.2%,为了得到与室内模型试验条件相似的初始冻结温度场和水分场,在冻结之前,对道面结构模型预降温处理,使其内部温度处于3~9 ℃;采取外部水分入渗试验,得到水分不均匀分布的冻结初始水分场.由于不考虑混凝土面层和水泥稳定层的含水率,故取值为0.湿密度取2 110 kg/m3,干密度取1 920 kg/m3,冻结时间取72 h.
2) 边界条件.果洛机场地下水位很低,地下水对冻深范围内土基含水率的影响非常小,故本文不考虑地下水补充,将底面设为隔水条件;本文主要研究道肩区及其相邻区域土基水热耦合问题,考虑到侧面和底面边界距离该区域较远且对其水热耦合运动影响甚微,同时为了简化次要因素,便于计算,将模型侧面和底面均取隔水绝热边界条件,侧面为水平约束,底面为固端约束.
2.3.3 各结构层的计算参数1) 混凝土面层的计算参数.混凝土面层的弹性模量取3×104 MPa,密度取2 400 kg/m3,导热系数取1.58 W·(m·K-1),泊松比取0.167,体积比热容取2 410.3 kJ·(m3·K)-1,质量比热容取1 004 J·(kg·K)-1.
2) 水泥稳定层的计算参数.水泥稳定层的弹性模量取1 400 MPa,密度取2 250 kg/m3,导热系数取1.36 W·(m·K-1),质量热容取1 190.7 J·(kg·K)-1,体积比热容取2 560.3 kJ·(m3·K)-1,泊松比取0.186.
3) 砂砾土层的计算参数.本文假设砂砾土层为各向同性体,砂砾土的干密度取1 920 kg/m3,初始含水率取19.2%,含泥量取15%,冰的密度取900 kg/m3,水相变潜热取334.16 kJ/kg;未冻砂砾土的导热系数取1.63 W·(m·K-1),质量热容取2 595 kJ·(m3·K)-1,弹性模量取160 MPa,泊松比取0.2;质量热容取2 215 kJ·(m3·K)-1,冻结砂砾土的导热系数取1.60 W·(m·K-1),弹性模量取180 MPa,泊松比取0.3.
3 试验结果与模拟结果对比分析 3.1 温度场图 7为冻结至72 h时的温度场分布云图.可以看出:平均冻结深度能达到25 cm左右,而在模型试验当中,冻结至72 h时,冻结深度能达到26 cm,二者吻合程度较高.
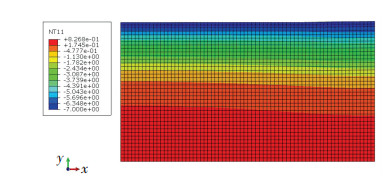
|
图 7 温度场分布云图 Figure 7 Temperature field distribution |
图 8为跑道区H=17 cm和H=34 cm深处温度的试验值与模拟值对比图.可以看出,二者的初始温度比较接近;冻结初期,二者的降温速率都比较大,随着冻结的进行逐渐变缓,当冻结到0 ℃左右时,二者的降温速率均明显变小,且都在0 ℃左右维持一段时间,然后温度再缓慢下降,从整体的温度随时间变化趋势来看,模型试验与数值模拟吻合度较高,说明该数值模型的温度场变化规律的可靠性较好.
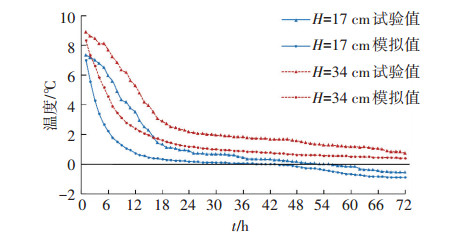
|
图 8 温度模拟值与试验值对比 Figure 8 Comparison of temperature between measured results and simulations |
分析模型试验及数值模拟的结果,得出以下温度场变化规律:温度梯度从大到小的顺序为:土面区,道肩区,跑道区,这一方面是因为混凝土的导热系数比砂砾土的导热系数小,另一方面,混凝土层和水泥稳定层对其下面的土基形成了一定的保温效果.冻结初期的降温速率较大,这是因为此时的温度梯度较大,而冻结中后期降温缓慢,一方面因为此时的温度梯度较小,另一方面是因为当温度下降到0 ℃时,水分在结冰的同时放出热量,这种冰水相变作用减缓了温度的下降.
3.2 水分场图 9为冻结至72 h时的水分场分布云图.可以看出:冻结后,在同一竖直方向上,含水率水随着深度的增加而减小;在同一深度处,含水率由大到小的顺序为:土面区,道肩区,跑道区.

|
图 9 水分场分布云图 Figure 9 Moisture field distribution |
图 10为冻结后的实测含水率沿深度分布的曲线.可以看出,在经历一个冻融循环之后,道面结构内同一深度处含水率由大到小的顺序也为:土面区,道肩区,跑道区.水分场在竖直方向的分布规律为分为3个阶段:含水率先随深度的增加而增加,在H=14 cm处达到最大值;随着深度的增加,含水率减小,在H=26 cm处达到最小值;当深度继续增加时,含水率又逐渐缓慢增大.在第1阶段(0~14 cm深度范围内),水泥混凝土道面面层和水泥稳定土基层中的含水率可以忽略不计,土面区上层因其温度梯度过大,水分来不及迁移就被原地冻结成冰,水分迁移的通道被阻塞,下部水分很难迁移至该区域,故其含水率并非是冻结区最大的.在第2阶段(14~26 cm),水热耦合作用随着深度增加而减弱,因此含水率随深度增加而减小;第3阶段(26~36 cm深度范围内),未冻结区中的水分在温度梯度的作用下不断向冻结区迁移,越靠近冻结锋面的土层水分迁移越剧烈,含水率则越小.
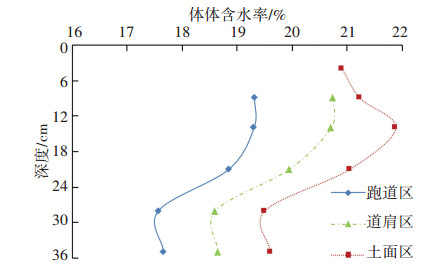
|
图 10 实测冻结后水分场分布 Figure 10 Measured volumetric water content after freezing |
对比分析图 9和图 10可知,模型试验所得到的竖直方向上的含水率分布规律看与数值模拟所得到规律大致吻合.分析模型试验及数值模拟的结果,得出以下温度场变化规律:随着冻结持续进行,负温从上而下传递,水分在温度梯度的作用下,不断由下部未冻结区向上部冻结区迁移、跑道区、道肩区向土面区迁移,含水率的增量即是温度梯度引起的水分迁移量.水分迁移总量由大到小的顺序为:土面区,道肩区,跑道区,以上现象正是水分与温度耦合作用的结果.
3.3 冻胀量由模型试验的监测结果可知,位移传感器的读数为103 μm数量级,而文献[19]表明水泥混凝土面层的翘曲变形量通常处于101 μm数量级.另外根据文献[20]所提出的当水泥混凝土面层浇筑时处于负温度梯度下,翘曲变形更加不明显的理论,本试验中水泥混凝土面层在冬季早期某天傍晚浇筑,浇筑时的环境温度约为10 ℃,并且是不断下降的,浇筑行为持续约半个小时,故满足负温度梯度的条件,因此翘曲变形相对较小.同时为了减小板边向上翘曲变形对冻胀量的干扰,试验中特意将位移传感器设置在距离板边4 cm处,另外在冻结过程时水泥混凝土面层所产生的温缩变形在一定程度上抵消了向上的翘曲变形量.综合以上分析,可排除水泥混凝土面层翘曲变形、温缩和干缩等其他作用对于冻胀量结果的干扰.
图 11为跑道和道肩的总冻胀量的试验值与模拟值对比分析图.可以看出,冻胀量的试验值与模拟值随时间变化的趋势基本吻合.二者均呈现先减小(即冻缩现象),再快速增加,然后缓慢增加,最后趋于平缓的总体趋势,与相关文献对冻胀基本过程的研究结果相同[3].试验值由于受到电压电流等不稳定因素的影响而波动较大,但其趋势与模拟值一致.

|
图 11 总冻胀量的试验值与模拟值对比 Figure 11 Comparison of frost heave between measured results and calculations |
在冻结至72 h左右时,道肩的总冻胀量为1.83 mm,跑道的总冻胀量为1.33 mm,两者相差0.5 mm,冻胀错台比较显著.说明具有较大含水率和含泥量且分布不均匀的道面结构的不均匀冻胀现象比较明显,在实际工程中所造成的冻胀变形量不容忽视.由于本次试验中土壤含水率不是很大,且无外界水分补充,因此总冻胀量不是很大.如果施工养护用水处理不当或降雨增多导致更多外部水分入渗,或有地下水补充,将会产生更大的冻胀,其危害将更加严重.
从以上室内模型试验与数值模拟的结果及其对比分析来看,跑道与道肩冻胀错台是道面结构内部水热耦合作用的结果.首先,道肩后于跑道施工使施工养护用水和雨水等外部水分充分入渗道肩下部土基,使得道肩下含水率大于跑道下含水率;其次,由于道肩面层薄于跑道面层,且靠近土面区,所以道肩区的温度梯度和降温速率大于跑道区;道肩面层对其下方土基的荷载作用小于跑道面层,所以道肩区的冻胀力大于跑道区.因此含水率更大的道肩区土基在更大的温度梯度和降温速率的作用下,水分迁移和积聚更加剧烈,因而冻胀更加剧烈,再加上道面面层的荷载作用对土基冻胀力的约束作用更小,因此最终道肩面层的变形比跑道面层更大,故而产生冻胀错台.
4 结论1) 施工养护用水和雨水等入渗道肩区土基对初始水分场影响较大,道肩区的含水率大于跑道区的含水率,上部冻结区的水分大于下部未冻结区的水分;这种水热耦合作用,是产生道面结构不均匀冻胀病害的根本原因.不均匀分布的初始水分场在不同的降温速率和温度梯度的作用下产生水分的迁移和积聚,在持续的水热耦合作用下,最终发生跑道与道肩不均匀冻胀错台.
2) 通过与模型试验及实际工程的对比验证,说明数值模型具有一定的确性和适用性.数值模拟有效地弥补了模型试验只能监测有限测点和有限断面的劣势,有助于更加全面地研究不均匀冻胀问题.
3) 囿于现场试验的实施难度及试验结果受到复杂的自然环境影响而不够精确和单纯地利用数值模拟认识水热耦合问题所存在的不可靠性,本文所采取的模型试验和数值模拟相结合的研究思路和实施方法为人们深入研究更多寒区构筑物不均匀冻胀病害提供了参考.
| [1] |
李安原, 牛永红, 牛富俊, 等. 粗颗粒土冻胀特性和防治措施研究现状[J]. 冰川冻土, 2015, 1(37): 202. LI Anyuan, NIU Yonghong, NIU Fujun, et al. Researchstatus of frost heaving properties and controlling measures of coarse grained soil[J]. Journal of Glaciology and Geocryology, 2015, 1(37): 202. DOI:10.7522/j.issn.1000-0240.2015.0023 |
| [2] |
岑国平, 龙小勇, 洪刚, 等. 青藏高原季冻区砂砾土冻胀特性试验[J]. 哈尔滨工业大学学报, 2016, 3(48): 53. CEN Guoping, LONG Xiaoyong, HONG Gang, et al. Frost heaving properties of gravel soil in seasonal frozen region of Qinghai-Tibet Plateau[J]. Journal of Harbin Institute of Technology, 2016, 3(48): 53. DOI:10.11918/j.issn.0367-6234.2016.03.009 |
| [3] |
SHENG D, ZHANG S, NIU F J, et al. A potential new frost heave mechanism in high-speed railway embankments[J]. Geotechnique, 2013, 64(2): 144. DOI:10.1680/geot.13.P.042 |
| [4] |
龙小勇, 岑国平, 蔡宛彤, 等. 砂砾土地基道面结构不均匀冻胀防治[J]. 空军工程大学(自然科学版), 2018, 1(19): 97. LONG Xiaoyong, CEN Guoping, CAI Wantong, et al. Prevention ofuneven frost heave of pavement structure on gravel soil foundation[J]. Journal of Air Force Engineering University(Natural Science Edition), 2018, 1(19): 97. DOI:10.3969/j.issn.1009-3516.2018.01.017 |
| [5] |
EIGENBROD K D. Effects of cyclic freezing and thawing on volume changes and permeability of soft fine-grained soils[J]. Canadian Geotechnical Journal, 1996, 33: 529. DOI:10.1139/t96-079-301 |
| [6] |
BILODEAU J P, DORE G, PIERRE P. Gradation influence on frost susceptibility of base granular materials[J]. International Journal of Pavement Engineering, 2008, 9: 397. DOI:10.1080/10298430802279819 |
| [7] |
ZHOU J Z, WEI C F, WEI H Z, et al. Experimental and theoretical characterization of frost heave and ice lenses[J]. Cold Regions Science and Technology, 2014, 104: 76. |
| [8] |
HENDRY M T, ONWUDE L U, SEGO D C. A laboratory investigation of the frost heave susceptibility of fine-grained soil generated from the abrasion of a diorite aggregate[J]. Cold Regions Science and Technology, 2016, 123: 91. DOI:10.1016/j.coldregions.2015.11.016 |
| [9] |
刘晓东. 路面容许冻胀与不均匀冻胀[J]. 黑龙江交通科技, 2006, 4: 37. LIU Xiaodong. Thefacultative frost heave and uneven frost heave of pavement[J]. Journal of Heilongjiang Transportation Science and Technology, 2006, 4: 37. DOI:10.3969/j.issn.1008-3383.2006.04.027 |
| [10] |
王殿威. 道路不均匀冻胀浅析[J]. 北方交通, 2007, 2: 28. WENG Dianwei. Briefanalysis for differential frost of road[J]. Northern Transportation, 2007, 2: 28. DOI:10.3969/j.issn.1673-6052.2007.02.011 |
| [11] |
SAARENKETO T, MATINTIPA A, VARIN P. The use of ground penetrating radar, thermal camera and laser scanner technology in asphalt crack detection and diagnostics[C]. 7th RILEM International Conference on Cracking in Pavements. Rovaniemi: Springer, 2012: 137
|
| [12] |
ROY L P, BURN C R. A modified landform development model for the topography of drained thermokarst lake basins in fine-grained sediments[J]. Earth Surface Processes and Landforms, 2016, 41: 1504. DOI:10.1002/esp.v41.11 |
| [13] |
WANG T F, LIU J K, TIAN Y D, et al. Frost jacking characteristics of screw piles by model testing[J]. Cold Regions Science and Technology, 2017, 138: 98. DOI:10.1016/j.coldregions.2017.03.008 |
| [14] |
岑国平, 龙小勇, 洪刚, 等. 含泥量对砂砾土冻胀特性的影响[J]. 科技导报, 2015, 5(33): 78. CEN Guoping, LONG Xiaoyong, HONG Gang, et al. Influence of silt content on frost heaving properties of gravel soil[J]. Science and Technology Review, 2015, 5(33): 78. DOI:10.3981/j.issn.1000-7857.2015.05.012 |
| [15] |
龙小勇, 岑国平, 蔡宛彤, 等. 压实度及水分对青藏高原季冻区砂砾土冻胀特性的影响[J]. 科技导报, 2018, 36(6): 112. LONG Xiaoyong, CEN Guoping, CAI Wantong, et al. Influence of compaction degree and moisture on frost heaving properties of gravel soil in seasonally frozen region of Qinghai-Tibetan Plateau[J]. Science and Technology Review, 2018, 36(6): 112. DOI:10.3981/j.issn.1000-7857.2018.06.014 |
| [16] |
王文杰.冻土水热力三场耦合的衬砌渠道冻胀数值模拟[D].杨凌: 西北农林科技大学, 2013 WANG Wenjie. Frostheaving simulation model of lining canals based on heat-moisture-stress coupled fields of frozen soils[D]. Yangling: Northwest Agriculture & Forestry University, 2013 http://cdmd.cnki.com.cn/Article/CDMD-10712-1013347604.htm |
| [17] |
XU X Z, OLIPHANT J L, TICE A R. Experimental study on factors affecting water migration in frozen morin clay[M]. Proceedings of the 4th International Symposium on Ground Freezing, 1985, 1: 123
|
| [18] |
KONRAD J M, MORGENSTERN N R. Prediction of frost heave in the laboratory during transient freezing[J]. Canadian Geotechnical Journal, 1982, 19: 250. DOI:10.1139/t82-032 |
| [19] |
傅琴. 半刚性基层与贫混凝土基层水泥路面翘曲变形分析[J]. 公路交通科技(应用技术版), 2008, 10: 52. FU Qin. Bucklingdeformation analysis of cement pavement of semi-rigid base and lean concrete cement pavement[J]. Journal of Highway and Transportation Research and Development(Application Technology Edition), 2008, 10: 52. |
| [20] |
曾惠珍. 水泥混凝土路面的温度梯度研究[J]. 四川理工学院学报(自然科学版), 2015, 5(28): 62. ZENG Huizhen. Study ontemperature gradient of the cement concrete pavement[J]. Journal of Sichuan University of Science & Engineering(Natural Science Edition), 2015, 5(28): 62. DOI:10.11863/j.suse.2015.05.12 |
 2018, Vol. 50
2018, Vol. 50


