2. 浙江大学 建筑工程学院,杭州 310058
2. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
延性断裂和低周疲劳是钢材的两种主要破坏方式.文献[1]根据试验提出了类似于Park-Ang指标形式的钢材损伤指标,即用最大塑性变形和滞回耗能的线性组合来表示损伤程度.其他研究,如文献[2-5]的钢材试验结果显示,低周疲劳损伤累积会降低材料的极限变形能力,塑性变形的绝对值也会减少材料的低周疲劳寿命.但文献[6]认为平均应变和最大塑性变形对低周疲劳寿命的影响很小;文献[7]的试验表明,当塑性变形较小时,低周疲劳寿命随塑性变形的增大而减小,当塑性变形较大时,低周疲劳寿命随之增加;文献[8]提出了由韧性损伤和低周疲劳损伤线性组合的修正Coffin-Manson公式,并指出只有当拉压塑性变形绝对值之和超过一定界限后,钢材的这两种破坏方式才会互相耦合.这些研究表明,学者们就两种破坏界限之间是否存在相关性尚未达成共识.另一方面,钢材在大幅值循环荷载作用下会发生明显的循环软化现象[1],可能会降低钢结构的抗震性能及震后承载能力.目前,常用的本构关系模型均不能考虑材料的循环软化特性. 1975年Dafalias等[9]首次提出双曲面本构关系模型(2SM),之后该模型受到了广泛关注,不少学者对其进行了改进.如文献[10]基于SS400、SM490和SM570钢材的拉压试验结果,引入了虚拟边界面,建立了屈服平台的消减判定公式,极大地提高了模型的计算精度;文献[11]通过Q345钢材的试验研究,对双曲面模型进行了相应的修正,提高了模型对小幅应变变化的应力路径预估精度;文献[12]通过试验校核了Q345钢材的双曲面本构模型参数,并认为常用的随动强化模型高估了钢桥在地震作用下的应变反应.此外,文献[13]建立了三曲面本构关系模型,提出了不连续曲面的概念.文献[14]通过试验研究,考察了循环荷载作用下三曲面模型对钢材棘轮效应的模拟.经过几十年的发展,多曲面本构关系模型可以同时考虑包辛格效应、材料强化、弹性域的缩小和移动、边界面的扩大以及屈服平台的减小至消失等力学特性.模型的计算精度也已在钢桥墩和钢拱肋的相关试验和计算分析中得到验证[15-21].然而,伴随低周疲劳进程而发生的循环软化特性尚不能得到考虑,制约着本构模型对钢结构抗震性能及震后承载能力的精确评估.
针对上述研究现状,本文以Q345qC钢材为例,通过试验讨论了钢材塑性变形极限和低周疲劳极限的相关性,考察了钢材的循环软化特性;通过对双曲面本构关系模型进行改进,使其可以考虑钢材的循环软化特性.最后,以钢桥墩为对象,研究了材料循环软化效应对结构地震承载力的影响.试验和分析结果可为建立钢结构地震破坏验算方法提供参考.
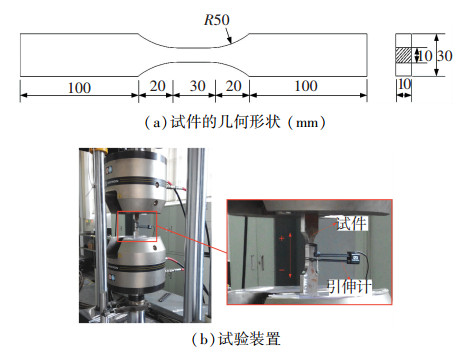
1 试验以Q345qC钢材为试验对象,图 1为试件尺寸和试验装置[22].试验方法参照文献[23]相关规定,采用INSTRON8802-250 kN电液伺服材料试验机进行加载,以应变作为控制加载的参数并采用引伸计测量应变.引伸计标距为25 mm,量程为-2.5~12.5 mm.当破坏发生在试验段以内时判定结果有效.
|
图 1 试件尺寸和试验装置 Figure 1 Size of the specimen and test set-up |
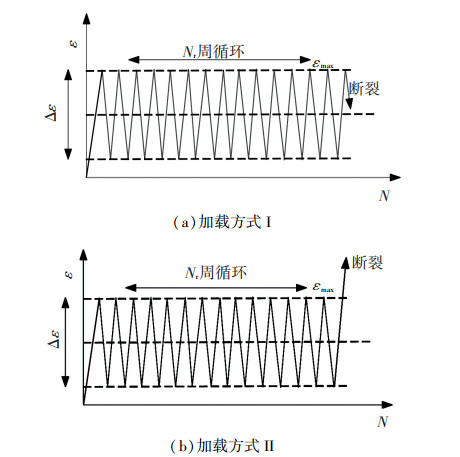
图 2为试验的加载方法.除单调拉伸试验外,还进行了在不同塑性变形条件下的低周疲劳试验以及先施加循环荷载作用再单调拉断的试验.其中,ε、εmax、Δε分别为试件所受的应变、循环应变的最大值和全应变幅,N、Nf分别为试件当前所经历的荷载循环次数及其疲劳寿命.在加载方式Ⅰ中,全应变幅为3.35%;在加载方式Ⅱ中的疲劳试验阶段,全应变幅分为3.35%和5.03%两组.
|
图 2 试验加载方法 Figure 2 Cyclic loading protocol |
根据试验,Q345钢材基本力学参数和双曲面本构模型材料参数如下:弹性模量E=204.0 GPa,初始屈服强度σy=402.1 MPa,极限强度σu=552.7 MPa,单调拉伸下屈服平台结束时刻的塑性应变εstp=1.01×10-2,塑性模量EstP=3.8 GPa,钢材边界面初始半径κ0和初始斜率E0P分别为425.0 MPa和2.55 GPa,泊松比μ=0.25.单调拉伸试验结果显示,钢材的延性较好,断后伸长率可达40.0%.
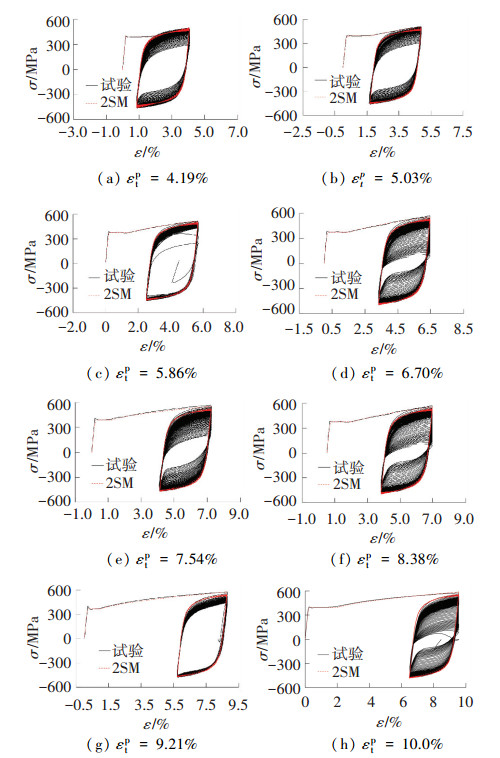
2.2 最大塑性变形对低周疲劳寿命的影响图 3给出了部分试件在加载方式Ⅰ作用下的应力-应变曲线.其中,σ为应力大小,εtp为钢材所经历的最大塑性应变.材料应力退化可以分成3个阶段:应力随荷载循环的快速下降,稳定地退化,退化加快并断裂.由于双曲面本构模型(2SM)不能考虑材料循环软化现象,除前几周循环外,模型预测的最大应力与试验结果差距较大.
|
图 3 加载方式Ⅰ作用下试件的应力-应变曲线 Figure 3 Stress-strain curves of the specimens under Load Case Ⅰ |
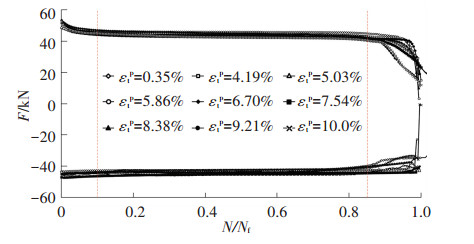
图 4为承载力-寿命曲线,F为抗拉或抗压峰值.本次试验表明,3个阶段分别约占疲劳总寿命的10%、75%和15%.钢材Q345qC具有明显的循环软化特征,其抗低周疲劳性能较好,在Δε=3.35%条件下疲劳寿命约200周.
|
图 4 试件的承载能力-循环周次曲线 Figure 4 Curves of the bearing capacity-load cycles of the specimen |
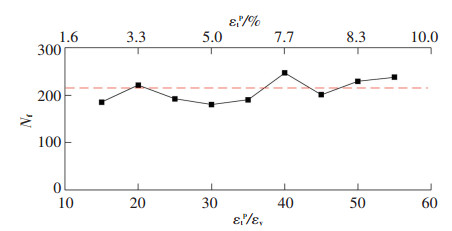
图 5为试件最大塑性变形对低周疲劳寿命的影响.其中εy为屈服应变大小. 图 5表明,当最大塑性应变不大于10%时,塑性变形最大值的增加不会明显降低钢材的低周疲劳寿命.
|
图 5 塑性应变对低周疲劳寿命的影响 Figure 5 Effects of plastic strain on the low-cycle fatigue life |
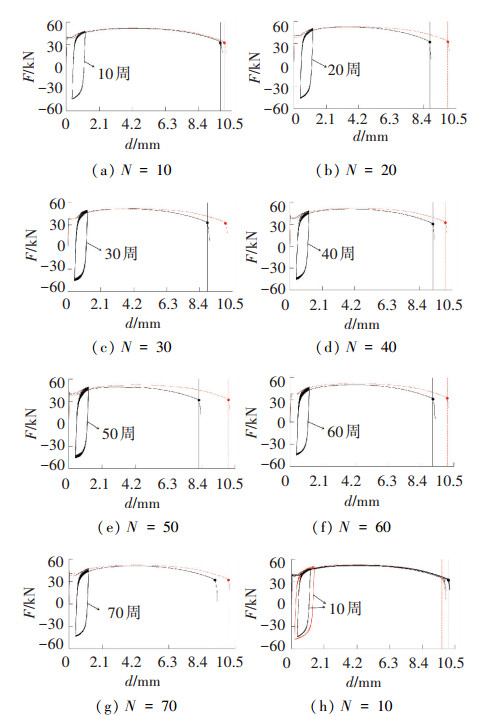
图 6给出了部分试件在加载方式Ⅱ作用下的荷载-位移曲线及单调拉伸试验结果.其中,d为材料变形量,虚线为单调拉伸试验结果. 图 6(h)同时还给出了全应变幅为5.03%时的试验结果. 图 6表明,经过塑性耗能后材料的极限变形能力虽有所下降,但这种影响并不明显.在大幅值应变循环70周内时,变形极限的下降基本小于15%.另外,应变幅的改变也未显著影响钢材的延性.
|
图 6 试件在加载方式Ⅱ作用下的荷载-位移曲线 Figure 6 Load-displacement curves of specimens under load Case Ⅱ |
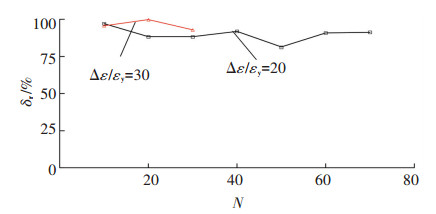
为方便与钢材的原有极限变形能力进行对比,将经受塑性耗能后的极限变形能力定义为钢材的剩余延性. 图 7为钢材的剩余延性δr与荷载循环次数N之间的关系. 图 7表明,延性受塑性损伤累积的影响不大.
|
图 7 低周疲劳损伤累积对延性极限的影响 Figure 7 Effects of low-cycle fatigue accumulation on ductility limit |
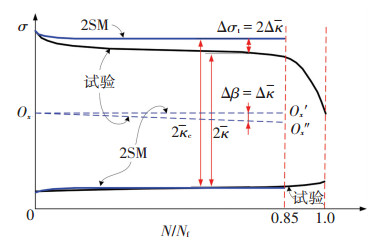
通过2.1节的试验结果可知,Q345钢材在高应变反复荷载作用下呈现出明显的循环软化现象.目前的双曲面模型(2SM)尚不能考虑该特征,导致其预测的应力峰值与试验差距较大.针对该问题,应对双曲面本构关系模型进行适当改进.由于在第三阶段呈现出的承载力快速下降具有较大的离散性,本节将仅考虑钢材在前两个阶段的循环软化特性.虽然在高应变反复荷载作用下钢材的抗拉承载力不断下降,然而抗压承载力变化较小.为使模型能够兼顾抗拉与压承载力的变化特性,需要将边界面中心向受拉的反方向移动Δβ,同时将边界面半径缩小Δκ,边界面中心的运动路径将由OxOx′变为OxOx″,如图 8所示.假定Δσt为峰值应力试验值和计算值之差,则有
| $ \left\{ \begin{gathered} \Delta \beta = \Delta \overline \kappa , \hfill \\ \Delta {\sigma _t} = 2\Delta \overline \kappa . \hfill \\ \end{gathered} \right. $ |
|
图 8 边界面的移动和缩小过程 Figure 8 Movement and shrinkage of the bounding surface |
传统的断裂力学常采用材料在单位体积上耗散的能量来预测断裂的发生,本节假定边界面半径的缩小规律与塑性能量密度Wp的对数函数有关,以方便本构关系模型与有限元方程的建立.根据材料试验结果,有
| $ \Delta \kappa = - A \cdot {\text{ln}}({W_{\text{p}}} - C \cdot W_{{\text{st}}}^{\text{p}}) + B. $ |
式中:Wstp为单调加载下屈服平台结束时刻的塑性能量密度,A、B、C为材料参数.方程中C·Wstp分项为当材料塑性能量密度达到一定程度时,循环软化特征才开始明显影响承载力.
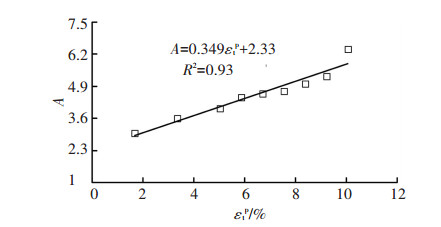
根据试验结果,参数B、C的平均值分别为8.3×107和9.0;参数A可由最小二乘法对试验结果拟合获得,如图 9所示.结果表明,材料所经历的最大塑性拉应变对循环软化有较大影响.
|
图 9 参数A与最大拉应力之间的试验关系 Figure 9 Relationship between parameter A and the maximum plastic strain |
由于对钢材进行复杂应力条件下的加载尚存在不少困难,借助于普通的万能材料试验机以及常规引伸计很难给试件施加人为可控的多向受力状态.目前,多向应力状态下的钢材本构模型大多是由单向受力状态推广而来[9-12],其合理性仍需相关三轴加载试验的验证.鉴于此,以下将给出了在多向应力状态下双曲面本构模型各变量的定义和计算方法,为复杂应力条件下本构关系模型的程序编制提供一种思路.此时,各种变量需要写成应力空间或应变空间中的张量形式.首先,在每个时间增量步中边界面中心的移动dβij可定义为
| $ {\text{d}}{\beta _{ij}} = {\text{d}}\kappa = - \frac{{A \cdot {\text{d}}{W_{\text{p}}}}}{{{W_{\text{p}}} - C \cdot W_{{\text{st}}}^{^{\text{p}}}}} \cdot {n_{ij}} \cdot \frac{T}{{\left| T \right|}}. $ |
式中:nij为塑性流动方向的单位张量,T为应力三轴度,T/|T|可用来判定材料处于受拉还是受压状态. nij与T可以表示为
| $ \left\{ \begin{array}{l} {n_{ij}} = \sqrt {\frac{3}{2}} \frac{{{S_{ij}} - {\alpha _{ij}}}}{\kappa },\\ T = \frac{{\frac{1}{3}\left( {{\sigma _1} + {\sigma _2} + {\sigma _3}} \right)}}{{\sqrt {\frac{1}{2}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _3} - {\sigma _1}} \right)}^2}} \right]} }}. \end{array} \right. $ |
式中:Sij为应力张量的偏量,αij、κ分别为屈服面或加载面的中心与半径,σ1、σ2、σ3分别为3个主应力大小.
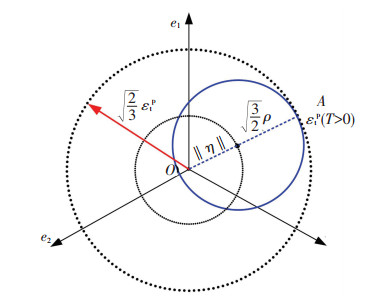
材料所经历的最大塑性拉应变可由图 10所示的应变偏量空间中的应变面获得.其中,实线曲面为等效塑性应变曲面,即双曲面本构理论中的A.E.P.S曲面;ηij和ρ分别为该曲面的中心和半径.在π平面内,等效塑性应变曲面上距离应变偏量空间中心最远的点即为材料经历的最大塑性拉应变,可表示为
| $ \varepsilon _t^p = \sqrt {\frac{2}{3}} \left\| {{\eta _{ij}}} \right\| + \rho . $ |
|
图 10 应变空间中最大塑性应变的定义 Figure 10 Definition of the maximum plastic strain in strain space |
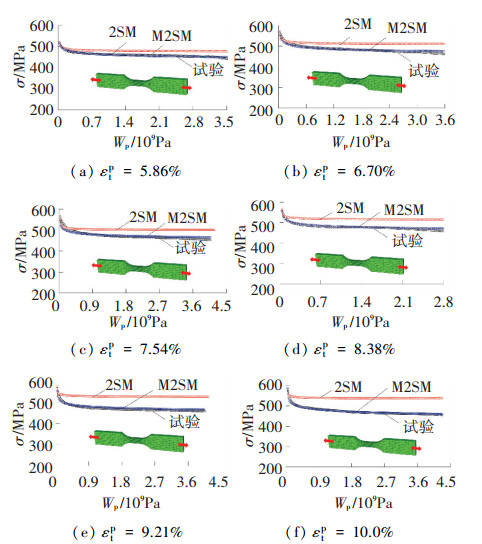
采用FORTRAN语言编制改进的双曲面本构关系模型程序,并通过用户子程序UMAT将其与通用软件ABAQUS实现数据对接,以验证本构关系模型的改进效果.有限元计算模型采用C3D8实体单元,在引伸计测量标距内的单元尺寸为1.0 mm,采用强制位移的加载方法. 图 11给出了试验、现有双曲面模型(2SM)和改进后双曲面模型(M2SM)的应力峰值与塑性耗能之间的关系.
|
图 11 低周疲劳前两阶段的应力峰值计算与试验结果 Figure 11 Peak strain calculation and test results in the first two stages of the low-cycle fatigue |
结果表明,除前几周荷载循环外,现有双曲面本构关系模型不能考虑材料的循环软化特征;但通过本文的改进,模型可以精确地预测出材料的承载力下降特征.
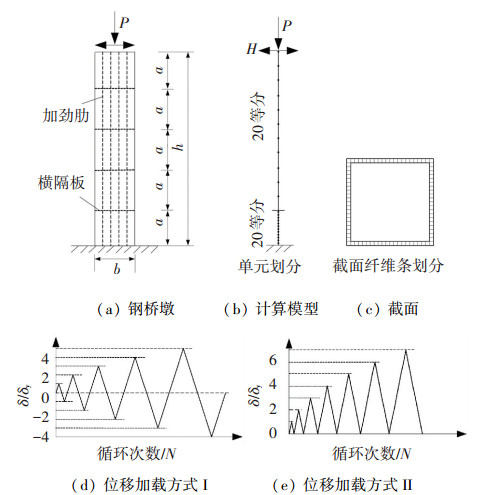
4 循环软化对构件地震承载力的影响 4.1 钢桥墩弹塑性静力分析以图 12所示的钢桥墩为研究对象,通过在其顶部施加竖向常轴力P和水平反复荷载H,可以考察钢材循环软化对构件弹塑性力学行为的影响[24].其中,h为桥墩高度,a为横隔板间距,b为截面的宽度.桥墩竖向常轴力为全截面屈服力的0.15倍,钢桥墩的结构设计符合日本桥梁抗震设计规范[25]的相关规定.采用纤维单元对其进行弹塑性静力分析,单元截面共划分为84个纤维条,并将带有纵向加劲肋的截面等效成无加劲肋截面.由于塑性主要发生于墩底,该部位布置了较密的单元.采用在墩顶施加逐渐增大的强制位移作为加载方式,加载方式又分为单向增大和双向同时增大的强制位移.其中,δ和δy分别为墩顶的强制位移和初始屈服位移.通过编制相应纤维单元的UMAT子程序将本构模型导入ABAQUS软件,计算过程还考虑了几何非线性的影响.
|
图 12 钢桥墩计算模型及加载方式 Figure 12 Analytical model and loading modes of the steel bridge pier |
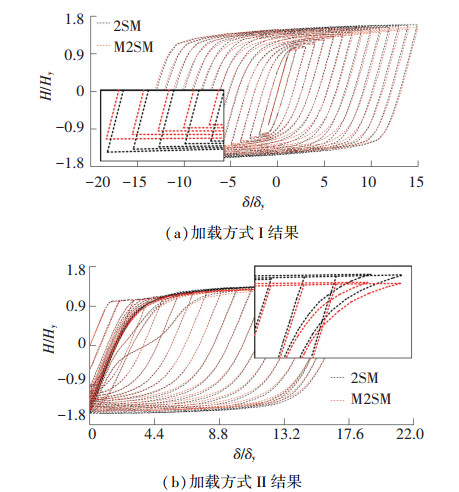
图 13给出了采用不同本构关系模型计算得到的墩顶荷载-位移曲线.其中,Hy为墩顶的初始屈服荷载[24].结果表明,考虑循环软化特性后构件的承载能力有所降低,但材料层面的循环软化对构件层面的承载力降低影响有限.当强制位移达到15δy时,考虑循环软化效应后钢桥墩的承载能力在两种加载情况下分别下降了4.0%和6.4%.
|
图 13 墩顶荷载-位移曲线 Figure 13 Load-displacement curves at steel pier top |
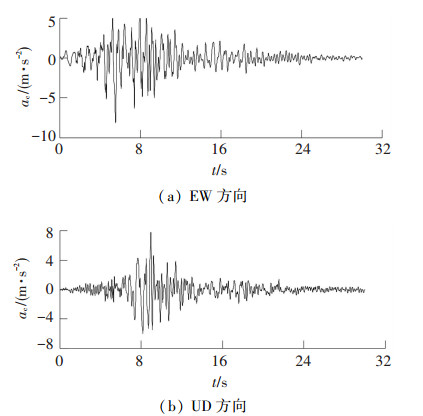
对前述钢桥墩输入地震动,以考察循环软化效应对钢桥墩弹塑性地震反应及震后承载能力的影响.为使钢桥墩进入充分的塑性状态,采用如图 14所示的阪神地震神户大学记录波作为激励.其中,ac为加速度,t为时间.将钢桥墩的轴力转化为墩顶等效质量,结构基频为1.89 Hz.动力计算采用隐式积分Newmark-β法(β=1/4),Rayleigh阻尼比为2.0%.此外,采用ABAQUS中的Restart功能对地震损伤后的钢桥墩进行Pushover分析,即在墩顶施加渐增的水平推力.
|
图 14 输入地震动 Figure 14 Input ground motion |
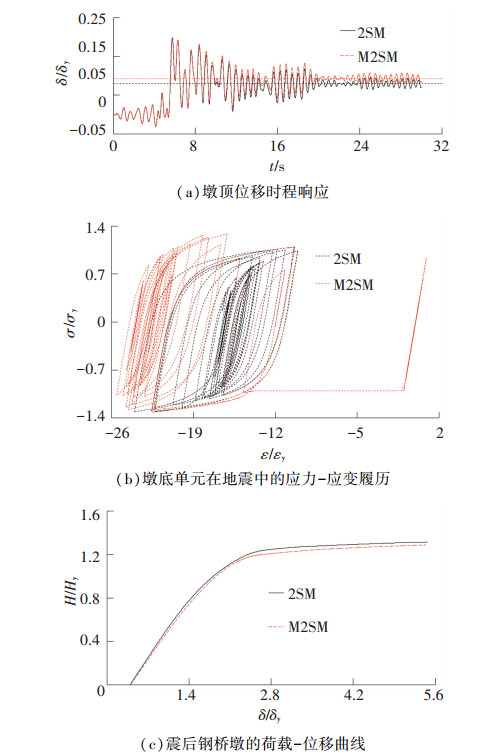
图 15给出了材料循环软化对钢桥墩地震反应及震后承载力的影响.其中,图 15(a)为墩顶的位移时程响应对比,图 15(b)为墩底损伤单元的应力-应变履历对比,图 15(c)为由Pushover分析得到的钢桥墩震后承载能力对比.结果表明,循环软化效应对钢桥墩最大位移响应的影响较小,但增大了构件的残余变形,增幅为17%;循环软化效应使墩底损伤单元的应变反应增大了6.4%,但震后承载能力的下降仅为3.3%.
|
图 15 钢桥墩地震反应和震后承载力 Figure 15 Seismic response and post-earthquake bearing capacity of the steel bridge pier |
1) Q345qC钢材的极限变形能力和抗低周疲劳性能较好,两种破坏界限之间的相关性不大.
2) Q345qC钢材在高应变反复荷载作用下呈现出明显的循环软化特征.基于试验结果,拟合出了承载力下降规律与材料塑性耗能密度之间的对数函数关系;当塑性拉应变较大时,材料的承载能力下降也更加明显.
3) 通过对边界面的移动和缩小,改进了现有的双曲面本构关系模型.试验和计算对比结果表明,改进后的本构模型能够精确地预测出材料的循环软化特征.
4) 考虑循环软化特性后,构件的承载能力有所降低,构件的弹塑性地震反应和震后承载能力也受到一定的影响,但材料层面的循环软化对构件层面的承载力降低影响有限.
5) 由于钢试件在较大的压应变作用下易发生屈曲,本次试验最大全应变幅仅为5%.今后将对更高应变幅下的超低周疲劳破坏作进一步的研究;同时,如何获得多向应力状态下的钢材本构关系也将成为未来努力的一个方向,以期为钢结构震后承载能力的精确评估提供依据.
| [1] |
YUAN Y, CUI J, MANG H A. Computational structural engineering[M]. Dordrecht: Springer, 2009.
|
| [2] |
SHI Y, WANG M, WANG Y. Experimental and constitutive model study of structural steel under cyclic loading[J]. Journal of Constructional Steel Research, 2011, 67(8): 1185. DOI:10.1016/j.jcsr.2011.02.011 |
| [3] |
SHI G, WANG M, BAI Y, et al. Experimental and modeling study of high-strength structural steel under cyclic loading[J]. Engineering Structures, 2012, 37: 1. DOI:10.1016/j.engstruct.2011.12.018 |
| [4] |
JIA L J, KUWAMURA H. Ductile fracture model for structural steel under cyclic large strain loading[J]. Journal of Constructional Steel Research, 2015, 106: 110. DOI:10.1016/j.jcsr.2014.12.002 |
| [5] |
KURODA M. Extremely low cycle fatigue life prediction based on a new cumulative fatigue damage model[J]. International Journal of Fatigue, 2002, 24(6): 699. DOI:10.1016/S0142-1123(01)00170-0 |
| [6] |
COLIN J, FATEMI A, TAHERI S. Fatigue behavior of stainless steel 304L including strain hardening, prestraining, and mean stress effects[J]. Journal of Engineering Materials and Technology, 2010, 132(2): 1. |
| [7] |
KANG G Z, LIU Y J, LI Z. Experimental study on ratchetting-fatigue interaction of SS304 stainless steel in uniaxial cyclic stressing[J]. Materials Science and Engineering A, 2006, 435-436: 396. DOI:10.1016/j.msea.2006.07.006 |
| [8] |
TATEISHI K, HANJI T, MINAMI K. A prediction model for extremely low cycle fatigue strength of structural steel[J]. International Journal of Fatigue, 2007, 29(5): 887. DOI:10.1016/j.ijfatigue.2006.08.001 |
| [9] |
DAFALIAS Y F, POPOV E P. A model of nonlinearly hardening materials for complex loading[J]. Acta Mechanica, 1975, 21(3): 173. DOI:10.1007/BF01181053 |
| [10] |
SHEN C, MAMAGHANI I H P, MIZUNO E, et al. Cyclic behavior of structural steels. Ⅱ: theory[J]. Journal of Engineering Mechanics, ASCE, 1995, 121(11): 1165. DOI:10.1061/(ASCE)0733-9399(1995)121:11(1165) |
| [11] |
王彤, 谢旭, 唐站站, 等. 考虑复杂应变历史的钢材修正双曲面滞回模型[J]. 浙江大学学报(工学版), 2015, 49(7): 1305. WANG Tong, XIE Xu, TANG Zhanzhan, et al. Modified two-surface hysteretic model considering complex strain history[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(7): 1305. |
| [12] |
WANG T, XIE X, SHEN C, et al. Effect of hysteretic constitutive models on elasto-plastic seismic performance evaluation of steel arch bridges[J]. Earthquakes and Structures, 2016, 10(5): 1089. DOI:10.12989/eas.2016.10.5.1089 |
| [13] |
後藤芳顕, 王慶雲, 高橋宣男. 繰り返し荷重下の鋼製橋脚の有限要素法による解析と材料構成則[J]. 土木学会論文集, JSCE, 1998, 591(I-43): 189. |
| [14] |
张静, 王哲. 循环荷载三面本构模型及与实验结果比较[J]. 哈尔滨工业大学学报, 2017, 49(6): 183. ZHANG Jing, WANG Zhe. A three-surface cyclic constitutive model and comparison between experimental and numerical results[J]. Journal of Harbin Institute of Technology, 2017, 49(6): 183. |
| [15] |
GOTO Y, JIANG K S, OBATA M. Stability and ductility of thin-walled circular steel columns under cyclic bidirectional loading[J]. Journal of Structural Engineering, 2006, 132(10): 1621. DOI:10.1061/(ASCE)0733-9445(2006)132:10(1621) |
| [16] |
後藤芳顯, 小山亮介, 藤井雄介, 等. 2方向地震動を受ける矩形断面鋼製橋脚の動特性と耐震照査法における限界値[J]. 土木学会論文集A, JSCE, 2009, 65(1): 61. |
| [17] |
後藤芳顯, 村木正幸, 海老澤健正. 2方向地震動を受ける円形断面鋼製橋脚の限界値と動的耐震照査法に関する考察[J]. 構造工学論文集A, JSCE, 2009, 55A: 629. |
| [18] |
高圣彬, 葛汉彬. 交替荷载作用下钢材本构模型的适用范围[J]. 中国公路学报, 2008, 21(6): 69. GAO Shengbin, GE Hanbin. Applicable range of steel constitutive models under cyclic load[J]. China Journal of Highway and Transport, 2008, 21(6): 69. DOI:10.3321/j.issn:1001-7372.2008.06.012 |
| [19] |
USAMI T, GAO S B, GE H B. Stiffened steel box columns. part 1: cyclic behavior[J]. Earthquake Engineering and Structural Dynamics, 2000, 29(11): 1691. DOI:10.1002/(ISSN)1096-9845 |
| [20] |
三好喬, 崎元達郎, 鶴田栄一, 等. 繰り返しねじり力を受ける鋼構造物の終局挙動解析における材料硬化則の影響[J]. 構造工学論文集A, JSCE, 2003, 49A: 403. |
| [21] |
刘乃藩, 高圣彬. 带肋圆形截面钢桥墩的延性性能预测[J]. 哈尔滨工业大学学报, 2017, 49(3): 138. LIU Naifan, GAO Shengbin. Ductility prediction of stiffened steel pipe-section bridge piers[J]. Journal of Harbin Institute of Technology, 2017, 49(3): 138. |
| [22] |
唐站站.钢桥弹塑性地震反应计算方法及钢材地震损伤指标研究[D].杭州: 浙江大学, 2016 TANG Zhanzhan. Research on seismic response evaluation method of steel bridges and seismic damage index of steel material[D]. Hangzhou: Zhejiang University, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10335-1016264188.htm |
| [23] |
金属材料轴向等幅低循环疲劳试验方法: GB/T 15248—2008[S].北京: 中国标准出版社, 2008 The test method for axial loading constant-amplitude low-cyclefatigue of metallic materials: GB/T 15248—2008[S]. Beijing: China Standard Press, 2008 |
| [24] |
宇佐美勉. 鋼橋の耐震·制震設計ガイドライン[M]. 東京: 技報堂出版, 2006.
|
| [25] |
Japanese Road Association. Specifications for highway bridges, part Ⅴ: seismic design[S]. Tokyo: Maruzen, 2002
|
 2018, Vol. 50
2018, Vol. 50



