制动防抱死系统(antilock brake system, ABS)在减少电动车辆交通安全事故发生率方面起到了至关重要的作用[1-2].随着乘客对车辆主动安全性能要求的日渐提升,ABS控制策略的研究一直都是前言热点[3].目前,应用于车辆滑移率控制方法主要有逻辑门限制控制[4-5]、模糊控制[6-7]、PID控制[8]和滑模变结构控制[9-11]等.
文献[3]为车辆制动系统设计了一种用于调节制动力矩大小的逻辑门限控制方法;文献[6]采用模糊直接自适应控制算法设计了一种防抱死控制器,将滑移率的跟踪误差和等效滑移率变化率作为控制系统的输入量;文献[7]将模糊逻辑策略结合了低速再生防抱死策略,提高了电机制动精度;文献[8]基于滑移率对制动力矩变化的灵敏度优化调整PID参数,实现了针对复合制动系统的自适应ABS控制;文献[9]开发了一种滑模-PWM算法,并应用于传统摩擦制动系统取得了良好的防抱死性能.
但是,上述的控制方法用于轮毂电机电动车辆进行防抱死控制时都有其局限性,比如:车辆逻辑门限制-ABS控制中的门限值的选取主要依赖于繁琐的变工况路面试验,但是很难适应实际行驶过程中复杂多变的路面状态;实施模糊逻辑控制和PID控制的成本相对较低,但其控制精度不佳;将滑模控制算法应用于车轮滑移率控制虽然具有较强的鲁棒性,其滑移率控制效果却无法时刻保证最佳.
线性二次型最优控制通过建立性能评价指标,可使被控系统获得优越的使用性能[12-13].但是,研究发现无法根据现有的线性二次型最优控制算法来设计轮毂电机电动车辆复合制动系统的防抱死控制器.因此,在基本不改变制动系统状态方程以及防抱死性能评控制目标的情况下,为车辆制动系统设计基于改进线性二次型最优控制方法的防抱死控制器,使得车辆在不同路面行驶工况下获得良好的滑移率控制效果具有重要意义.
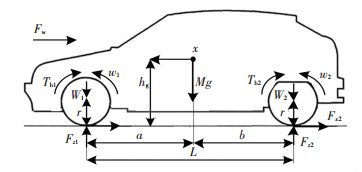
1 数学模型 1.1 车辆纵向动力学模型本文将半车制动模型作为研究对象,车辆制动模型见图 1.
|
图 1 车辆制动模型 Figure 1 Braking model of vehicle |
对图 1进行纵向动力学分析,可得汽车制动方程式为
| $ \begin{array}{l} \delta M\ddot x = - {F_{{\rm{x1}}}} - {F_{{\rm{x2}}}} - {F_{{\rm{f1}}}} - {F_{{\rm{f2}}}} - {F_{\rm{w}}} = \\ - {F_{{\rm{z1}}}}\mu \left( {{\lambda _1}} \right) - {F_{{\rm{z2}}}}\mu \left( {{\lambda _2}} \right) - {W_1}f - {W_2}f - \frac{{{C_{\rm{D}}}A\rho }}{2}{{\dot x}^2}. \end{array} $ | (1) |
式中:M为汽车质量,δ为汽车旋转质量换算系数,ẍ为车辆行驶加速度,Fx1、Fx2分别为前、后车轮的地面切向反作用力,Ff1、Ff2分别为前、后车轮的滚动阻力,Fz1、Fz2分别为前、后车轮的地面法向反作用力,Fw为空气阻力,μ(λ1)、μ(λ2)分别为前、后车轮与地面的附着系数,f为滚动阻力系数,CD为空气阻力系数,A为迎风面积,ρ为空气密度.
Fz1和Fz2的表达式分别为
| $ {F_{{\rm{z1}}}} = M\left( {g\frac{b}{L} - \ddot x\frac{{{h_{\rm{g}}}}}{L}} \right), $ | (2) |
| $ {F_{{\rm{z2}}}} = M\left( {g\frac{a}{L} + \ddot x\frac{{{h_{\rm{g}}}}}{L}} \right). $ | (3) |
式中a、b分别为质心到前、后轴的距离,L为轴距,hg为质心高度.
此外,前、后车轮运动状态的动力学方程[14]为
| $ \left\{ \begin{array}{l} I{{\ddot \theta }_1} = r{F_{{\rm{x1}}}} - {T_{{\rm{b1}}}} - {T_{{\rm{f1}}}} = r{F_{{\rm{x1}}}} - {T_{{\rm{b1}}}} - {F_{{\rm{f1}}}}r, \\ I{{\ddot \theta }_2} = r{F_{{\rm{x2}}}} - {T_{{\rm{b2}}}} - {T_{{\rm{f2}}}} = r{F_{{\rm{x2}}}} - {T_{{\rm{b2}}}} - {F_{{\rm{f2}}}}r. \end{array} \right. $ | (4) |
式中:I为车轮转动惯量,r为车轮有效半径,
Tb1和Tb2的表达式分别满足
| $ {T_{{\rm{b1}}}} = {T_{{\rm{m1}}}} + {T_{{\rm{h1}}}}, $ | (5) |
| $ {T_{{\rm{b2}}}} = {T_{{\rm{m2}}}} + {T_{{\rm{h2}}}}. $ | (6) |
式中Tm1、Tm2分别为前、后轮的电机制动力矩,Th1、Th2分别为前、后轮的液压制动力矩.
1.2 轮毂电机模型本文研究的电动车辆中前、后车轮分别安装可以相互独立驱动/制动的轮毂电机.轮毂电机类型为永磁同步电机PMSM,在dq坐标系下PMSM电机的数学模型为
| $ \left\{ \begin{array}{l} {{\dot i}_d} = \frac{{{u_d}}}{{{L_d}}} - \frac{{R{i_d}}}{{{L_d}}} + \frac{{pw{i_q}{L_q}}}{{{L_d}}}, \\ {{\dot i}_q} = \frac{{{u_q}}}{{{L_q}}} - \frac{{R{i_q}}}{{{L_q}}} - \frac{{pw{i_q}{L_q}}}{{{L_q}}} - \frac{{{\psi _{\rm{f}}}pw}}{{{L_q}}}, \\ {T_{\rm{m}}} = 1.5p\left[ {{\psi _{\rm{f}}}{i_q} + \left( {{L_d} - {L_q}} \right){i_d}{i_q}} \right]. \end{array} \right. $ | (7) |
式中:ud和uq分别为d、q轴电压,id和iq分别为d、q轴电流,Ld和Lq分别为d、q轴电感,R为相电阻,p为极对数,ψf为电机磁链,w为转子角速度,Tm为电机制动力矩.
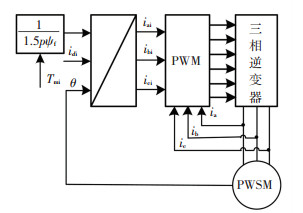
采用round转子结构,Ld=Lq,电机制动力矩简化为Tm=1.5pψfiq.因此,电机制动力矩可以通过控制q轴电流iq来获得. PMSM电机的力矩跟踪控制原理见图 2.其中θ为转子转角,iqi、idi分别为q和d轴的期望电流,iai、ibi、ici分别为a、b、c相的期望电流;ia、ib、ic分别为a、b、c相的实际电流.
|
图 2 PMSM电机的力矩跟踪控制原理 Figure 2 Scheme of PMSM's torque tracking control |
如图 2所示,基于式(7)中的电磁-转矩方程,以期望电机制动力矩Tmi来求取期望iqi,结合极对数、转角约束及理想idi=0的条件,三相期望电流iai、ibi和ici的坐标变换公式为
| $ \left[ {\begin{array}{*{20}{c}} {{i_{{\rm{ai}}}}}\\ {{i_{{\rm{bi}}}}}\\ {{i_{{\rm{ci}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }\\ {\cos \left( {\theta - \frac{2}{3}{\rm{ \mathit{ π} }}} \right)}&{ - \sin \left( {\theta - \frac{2}{3}{\rm{ \mathit{ π} }}} \right)}\\ {\cos \left( {\theta - \frac{2}{3}{\rm{ \mathit{ π} }}} \right)}&{ - \sin \left( {\theta - \frac{2}{3}{\rm{ \mathit{ π} }}} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_{d{\rm{i}}}}}\\ {{i_{q{\rm{i}}}}} \end{array}} \right]. $ | (8) |
将iai、ibi、ici与ia、ib、ic求差值输入滞环电流控制单元,得到三相逆变器的6个开关器件的控制开关信号,进而控制上述开关的接通与断开,最终实现对PMSM电机的力矩跟踪控制.
1.3 液压系统模型液压制动系统是轮毂电机电动车辆制动系统中的主制动器,建立液压制动系统的动态模型[15]为
| $ \begin{array}{l} \frac{{{\rm{d}}{P_{\rm{w}}}}}{{{\rm{d}}t}} = \frac{1}{{{C_{\rm{e}}}{R_{\rm{e}}}}}\sqrt {{P_{\rm{m}}} - {P_{\rm{w}}}} {u_1}\left( {t - {\tau _{{\rm{vp}}}}} \right) - \\ \;\;\;\;\;\;\;\;\;\frac{1}{{{C_{\rm{e}}}{{R'}_{\rm{e}}}}}\sqrt {{P_{\rm{w}}} - {P_{\rm{r}}}} {u_2}\left( {t - {{\tau '}_{{\rm{vp}}}}} \right) = \\ \;\;\;\;\;\;\;\;\;37.534\sqrt {{P_{\rm{m}}} - {P_{\rm{w}}}} {u_1}\left( {t - {\tau _{{\rm{vp}}}}} \right) - \\ \;\;\;\;\;\;\;\;\;38.313\sqrt {{P_{\rm{w}}} - {P_{\rm{r}}}} {u_2}\left( {t - {{\tau '}_{{\rm{vp}}}}} \right), \end{array} $ | (9) |
式中:pm为主缸压力,pw为轮缸压力,pr为低压储能器压力,Ce为等效液容特性系数,Re、Re′分别为增、减压过程中等效液阻等效系数,τvp、τvp′分别为增压和减压过程中进、出液阀及管路传输的滞后时间,u1、u2分别为进、出液阀的控制指令信号.
当u1=1,u2=0时,系统为增压状态;当u1=0,u2=1时,系统为减压状态;当u1=0,u2=0时,系统为保压状态.并常用一阶惯性环节来表征调压过程中的油压变化产生的时间延迟,即
| $ {T_{\rm{h}}}\left( s \right) = {P_{\rm{w}}}\left( s \right)\frac{{{K_{\rm{b}}}}}{{\tau s + 1}}. $ | (10) |
式中:Th(s)和Pw(s)分别为实际制动力矩和目标制动力矩,τ为反映制动器动态特性的常数,Kb为制动力矩常数.
2 现有线性二次型最优算法的防抱死控制分析现有线性二次型最优控制算法在控制过程中应该满足两个前提条件:1)控制系统是线性的,如果控制系统本身是非线性的则需要采用适当的线性化方法对系统中的若干非线性项进行线性化处理,且该线性系统(或者线性化后系统)的数学模型可以写成状态方程表达式;2)能够提出可以量化计算的综合性能评价指标J,该性能指标可以写成关于状态向量X和(或)控制向量U的二次型函数的积分形式.
采用现有线性二次型最优算法进行防抱死控制过程中,定义前、后轮滑移率λ1和λ2分别为
| $ {\lambda _1} = \frac{{\dot x - {{\dot \theta }_1}r}}{{\dot x}}, $ | (11) |
| $ {\lambda _2} = \frac{{\dot x - {{\dot \theta }_2}r}}{{\dot x}}. $ | (12) |
设定前、后轮的理想滑移率值都为0.2,根据理想滑移率来设置制动防抱死综合性能评价指标J,并将J改写成标准二次型形式,满足:
| $ \begin{array}{l} J = \frac{1}{T}\int_0^t {\left[ {{{\left( {0.8\dot x - r{{\dot \theta }_1}} \right)}^2} + {{\left( {0.8\dot x - r{{\dot \theta }_1}} \right)}^2}} \right]{\rm{d}}t} = \\ \;\;\;\;\;\;\frac{1}{T}\int_0^t {\left[ {{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{QX}} + 2{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{NU}} + {\mathit{\boldsymbol{U}}^\rm{T}}\mathit{\boldsymbol{RU}}} \right]{\rm{d}}t} , \end{array} $ | (13) |
| $ \mathit{\boldsymbol{N}} = \left[ {{{\bf{0}}_{5 \times 2}}} \right], \;\;\;\;\mathit{\boldsymbol{R}} = \left[ {{{\bf{0}}_{2 \times 2}}} \right], $ |
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{2 \times 2}}}&{{{\bf{0}}_{2 \times 3}}}\\ {{{\bf{0}}_{3 \times 2}}}&{\left[ {\begin{array}{*{20}{c}} {1.28}&{ - 0.8r}&{ - 0.8r}\\ { - 0.8r}&{{r^2}}&0\\ { - 0.8r}&0&{{r^2}} \end{array}} \right]} \end{array}} \right]. $ |
式中t为车辆制动时间.由式(1)~(4)所示的车辆制动模型,建立制动系统的状态向量并建立状态方程为
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{c}} {{\theta _1}}&{{\theta _2}}&{\dot x}&{{{\dot \theta }_1}}&{{{\dot \theta }_2}} \end{array}} \right]^{\rm{T}}}, $ | (14) |
| $ \mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{BU}} + \mathit{\boldsymbol{GW}}, $ | (15) |
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_{2 \times 3}}}&{{\mathit{\boldsymbol{I}}_{2 \times 2}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 2}}} \end{array}} \right], \mathit{\boldsymbol{B}} = \left[ \begin{array}{l} {{\bf{0}}_{3 \times 2}}\\ - {\mathit{\boldsymbol{I}}_{2 \times 2}} \end{array} \right], \mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{T_{{\rm{b1}}}}}\\ {{T_{{\rm{b2}}}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&0\\ 0&0&0&0&0\\ { - \frac{1}{{\delta M}}}&{ - \frac{1}{{\delta M}}}&{ - \frac{1}{{\delta M}}}&{ - \frac{1}{{\delta M}}}&{ - \frac{1}{{\delta M}}}\\ {\frac{r}{I}}&0&{ - \frac{r}{I}}&0&0\\ 0&{\frac{r}{I}}&0&{ - \frac{r}{I}}&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{W}} = {\left[ {\begin{array}{*{20}{c}} {{F_{{\rm{x1}}}}}&{{F_{{\rm{x2}}}}}&{{F_{{\rm{f1}}}}}&{{F_{{\rm{f2}}}}}&{{F_{\rm{w}}}} \end{array}} \right]^{\rm{T}}}. $ |
最优算法实施的核心步骤是构建符合控制目标的黎卡提方程,并求取最优控制向量U.基于轮毂电机电动车辆理想的状态方程以及标准的二次型防抱死综合性能评价指标,理想控制向量满足:
| $ \mathit{\boldsymbol{U}} = - \mathit{\boldsymbol{KX}}, $ | (16) |
| $ \mathit{\boldsymbol{K}} = - {\mathit{\boldsymbol{R}}^{ - 1}}{\left( {\mathit{\boldsymbol{SB}} + \mathit{\boldsymbol{N}}} \right)^{\rm{T}}}, $ | (17) |
式中S为黎卡提方程的唯一解.黎卡提方程为
| $ \mathit{\boldsymbol{AS}} + \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{A}}^{\rm{T}}} - \left( {\mathit{\boldsymbol{SB}} + \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{R}}^{ - 1}}{\left( {\mathit{\boldsymbol{SB}} + \mathit{\boldsymbol{N}}} \right)^{\rm{T}}} + \mathit{\boldsymbol{Q}} = 0. $ | (18) |
基于图 1所建立的车辆制动数学模型表达式可以写成式(15)中Ẋ=AX+BU+GW的表达形式,且式(13)所示的综合性能评价指标J能够用关于状态向量X和(或)控制向量U的二次型函数的积分形式表达.因此,使用现有的线性二次型最优控制算法来实施电动车辆防抱死控制的过程中,上述两个前提条件都能被满足.
但是,线性二次型最优控制算法在使用过程中,除了需要满足上述两个前提条件外,还需要再考虑使用的约束性,即需要另外满足3个使用条件:1)表征受控系统结构特性的状态矩阵A应该由控制矩阵B可控,即状态矩阵A的任意一行所对应的状态变量中都需要具备正刚度或者正阻尼特性,保证其是最小相位系统. 2)状态变量加权矩阵Q应该具有对称非负定的性质. 3)控制变量加权矩阵R的行列式值应该大于0.若基于该控制算法在设计防抱死控制器的过程中,上述使用条件中有任意一条或者多条不满足,则无法根据黎卡提方程求出唯一解S,进而导致控制向量U无法求解.由式(10)和(12)可得:根据上述控制方法来设计轮毂电机电动车辆的防抱死控制器时,理想的状态矩阵A中三至五行所对应的状态变量中不具有正刚度或者正阻尼特性,因此状态矩阵A不受控制矩阵B控制;理想的状态变量加权矩阵Q不具有对称非负定的性质;此外,控制变量加权矩阵R的行列式值等于0.
上述三条使用条件全部无法满足,所以无法基于理想的制动系统状态方程以及标准的防抱死综合性能评价指标设计出车辆防抱死控制器.
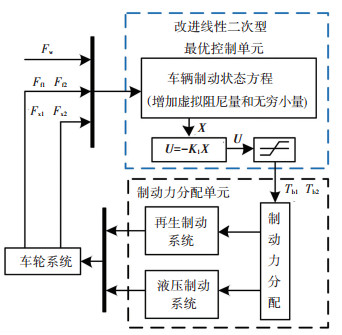
3 基于改进线性二次型最优算法的防抱死控制分析为了解决上述问题,本文提出了一种改进线性二次型最优控制算法,并将其应用在电动车辆防抱死控制系统的设计中,基于改进线性二次型最优算法的防抱死控制框图如图 3所示.
|
图 3 基于改进线性二次型最优算法的防抱死控制框图 Figure 3 Control scheme of ABS based on improved linearquadratic optimal method |
图 3控制系统主要由改进线性二次型最优控制单元和制动力分配单元两部分组成.其中,改进线性二次型最优控制单元的主要贡献在于:在建立黎卡提方程的过程中通过增加虚拟阻尼量以及无穷小量的方法,使得控制算法满足第2节所述的3个设计条件,计算出防抱死控制过程中作用在前、后轮上的理想制动力矩值,并对理想制动力矩的输出范围进行限定;而制动力分配单元的作用是按照事先设定好的制动力分配控制策略对理想制动力矩值进行分配,以获得实际的作用在前、后轮上的液压制动力矩和电机制动力矩.改进线性二次型最优控制算法和制动力分配控制策略分别阐述如下.
3.1 改进线性二次型最优控制算法提出改进线性二次型最优控制算法的目的在于解决第2节中提到的现有线性二次型最优控制算法因为不满足3个使用条件而无法应用于防抱死控制系统设计的缺陷.需要特别说明的是:采用改进线性二次型最优控制算法仍然要求满足第2节中关于提及的两个前提条件.在电动车辆防抱死控制过程中,改进线性二次型最优控制具体实施步骤如下.
首先,根据图 1所示的电动汽车制动模式的受力示意情况,建立增加了关于车辆速度的正阻尼项
| $ \left\{ \begin{array}{l} \ddot x \approx - \frac{1}{{\delta M}}\left( {{F_{{\rm{x1}}}} + {F_{{\rm{x2}}}} + {F_{{\rm{f1}}}} + {F_{{\rm{f2}}}} + {F_{\rm{w}}}} \right) + {c_{\rm{x}}}\dot x, \\ {{\ddot \theta }_1} \approx \frac{r}{I}{F_{{\rm{x1}}}} - \frac{1}{I}{T_{{\rm{b1}}}} - \frac{1}{I}{T_{{\rm{f1}}}} + {c_{{{{\rm{ \mathit{\dot θ} }}}_1}}}{{\dot \theta }_1}, \\ {{\ddot \theta }_2} \approx \frac{r}{I}{F_{{\rm{x2}}}} - \frac{1}{I}{T_{{\rm{b2}}}} - \frac{1}{I}{T_{{\rm{f2}}}} + {c_{{{{\rm{ \mathit{\dot θ} }}}_2}}}{{\dot \theta }_2}. \end{array} \right. $ | (19) |
状态向量X中的变量ẍ、
| $ \mathit{\boldsymbol{\dot X}} = {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{BU}} + \mathit{\boldsymbol{GW}}, $ | (20) |
式中A1为改写后的状态矩阵,满足
| $ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0&0&1&0\\ 0&0&0&0&1\\ 0&0&{{c_{\dot x}}}&0&0\\ 0&0&0&{{c_{\dot \theta 1}}}&0\\ 0&0&0&0&{{c_{\dot \theta 2}}} \end{array}} \right]. $ |
若ċxẋ、
其次,对标准的防抱死综合性能评价指标J进行改写,增加关于前、后车轮转角以及控制力矩的无穷小量
| $ \begin{array}{*{20}{c}} {{J_1} = J + \frac{1}{T}\int_0^t {\left[ {{\delta _{{\theta _1}}}{\theta _1}^2 + {\delta _{{\theta _2}}}{\theta _2}^2 + {\delta _{{T_{{\rm{b1}}}}}}{T_{{\rm{b1}}}}^2 + {\delta _{{T_{{\rm{b2}}}}}}{T_{{\rm{b2}}}}^2} \right]{\rm{d}}t} = }\\ {\frac{1}{T}\int_0^t {\left[ {{\mathit{\boldsymbol{X}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}_1}\mathit{\boldsymbol{X}} + 2{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{NU}} + {\mathit{\boldsymbol{U}}^{\rm{T}}}{\mathit{\boldsymbol{R}}_1}\mathit{\boldsymbol{U}}} \right]{\rm{d}}t} , } \end{array} $ | (21) |
| $ {\mathit{\boldsymbol{Q}}_1} = \left[ {\begin{array}{*{20}{c}} {{\delta _{{\theta _1}}}}&0&0&0&0\\ 0&{{\delta _{{\theta _2}}}}&0&0&0\\ 0&0&{1.28}&{ - 0.8r}&{ - 0.8r}\\ 0&0&{ - 0.8r}&{{r^2}}&0\\ 0&0&{ - 0.8r}&0&{{r^2}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_1} = \left[ {\begin{array}{*{20}{c}} {{\delta _{{T_{{\rm{b1}}}}}}}&0\\ 0&{{\delta _{{T_{{\rm{b2}}}}}}} \end{array}} \right]. $ |
由式(19)可得:Q1具有对称非负定性质,且矩阵R1的行列式值大于0恒成立.当
然后,基于改写后的车辆制动系统理想的状态方程以及二次型防抱死综合性能评价指标J1,构建黎卡提方程.理想控制力矩的求取表达式为
| $ \mathit{\boldsymbol{U}} = - {\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{X}}, $ | (22) |
| $ {\mathit{\boldsymbol{K}}_1} = - {\mathit{\boldsymbol{R}}_1}^{ - 1}{\left( {{\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{N}}} \right)^{\rm{T}}}, $ | (23) |
| $ {\mathit{\boldsymbol{A}}_1}{\mathit{\boldsymbol{S}}_1} + \mathit{\boldsymbol{SA}}_1^{\rm{T}} - \left( {{\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{N}}} \right){\mathit{\boldsymbol{R}}_1}^{ - 1}{\left( {{\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{N}}} \right)^{\rm{T}}} + {\mathit{\boldsymbol{Q}}_1} = {\bf{0}}. $ | (24) |
为了进一步削弱液压制动系统的时滞影响,增加改进线性二次型最优算法的可靠性,可以通过预估的路面附着系数û(λ)以及车轮角加速度来求取前、后轮制动力矩的预估值
| $ {{\bar T}_{{\rm{b1}}}} = rM\left( {g\frac{b}{L} - \ddot x\frac{{{h_g}}}{L}} \right)\hat u\left( \lambda \right) - I{{\ddot \theta }_1}, $ | (25) |
| $ {{\bar T}_{{\rm{b2}}}} = rM\left( {g\frac{a}{L} + \ddot x\frac{{{h_g}}}{L}} \right)\hat u\left( \lambda \right) - I{{\ddot \theta }_2}. $ | (26) |
最后,对前、后轮理想制动力矩的输出范围进行约束,约束关系为
| $ \left\{ \begin{array}{l} 0.8{{\bar T}_{{\rm{b1}}}} \le {T_{{\rm{b1}}}} \le 1.2{{\bar T}_{{\rm{b1}}}}, \\ 0.8{{\bar T}_{{\rm{b2}}}} \le {T_{{\rm{b2}}}} \le 1.2{{\bar T}_{{\rm{b2}}}}. \end{array} \right. $ | (27) |
改进线性二次型最优控制算法在实施防抱死控制过程中并没有改变如式(15)中状态方程以及式(13)中制动防抱死综合性能评价指标J的本质特性,所以改进线性二次型最优控制算法同样满足两个前提条件.其创新之处在于通过在构建黎卡提方程的过程中增加正阻尼项以及无穷小量的方法,使得改进线性二次型最优控制算法满足了第2节所述的3个基本使用条件.因此,该算法可以用于轮毂电机电动车辆的防抱死控制器设计.
3.2 复合制动系统的制动力分配控制策略为了在保证制动稳定性的前提下,充分发挥轮毂电机响应迅速和控制精确的特性优势,文本采用文献[16]所提供的制动力分配控制策略:1)低附着路面上,由主制动器提供基础制动力矩,轮毂电机实现防抱死协调. 2)中附着路面上,由轮毂电机提供基础制动力矩,通过调节液压制动力矩大小实现防抱死协调. 3)高附着路面上,轮毂电机不参与防抱死控制,由液压制动系统单独完成防抱死控制.
4 仿真分析本节中模拟了3种不同路面附着系数的制动工况,对采用有改进线性二次型最优控制器和滑模控制器的防抱死系统的ABS控制性能进行了对比分析.设定电动车辆的初速度为120 km/h,在紧急制动末尾采用通用算法,即车速低于15 km/h时退出ABS控制.
虚拟阻尼量以及无穷小量的取值应该平衡控制精确性和计算复杂性的关系,在保证防抱死控制器对理想滑移率的追踪精确的前提下兼顾考虑计算的复杂程度,进而降低控制成本.复合制动系统和车辆参数为M=650 kg; δ=1.05; a=1.53 m; b=1.55 m; L=3.08 m; hg=0.77 m; ρ=1.225 8 kg/m3; CD=0.38; A=2.57 m2; I=2.6 kg·m2; r=0.327 m; p=23; ψf=0.08 Wb; R=0.031 Ω; Lq=700 μH; ċx=10-6;
为了进一步量化评价电动车辆车轮滑移率控制效果的好坏程度,前、后轮滑移率控制精度采用如式(28)所示的滑移率均方根误差eλ来表征,eλ的表达式为
| $ {e_\lambda } = \int_0^t {\left[ {{{\left( {{\lambda _1} - 0.2} \right)}^2} + {{\left( {{\lambda _2} - 0.2} \right)}^2}} \right]{\rm{d}}t} . $ | (28) |
控制器1和控制器2分别表示基于改进线性二次型最优控制算法的防抱死控制器和基于滑模控制算法的防抱死控制器.限于篇幅,仿真结果中仅给出后轮滑移率和制动力矩与时间变化曲线用以评价采用了改进线性二次型最优控制器的电动汽车的防抱死控制效果.
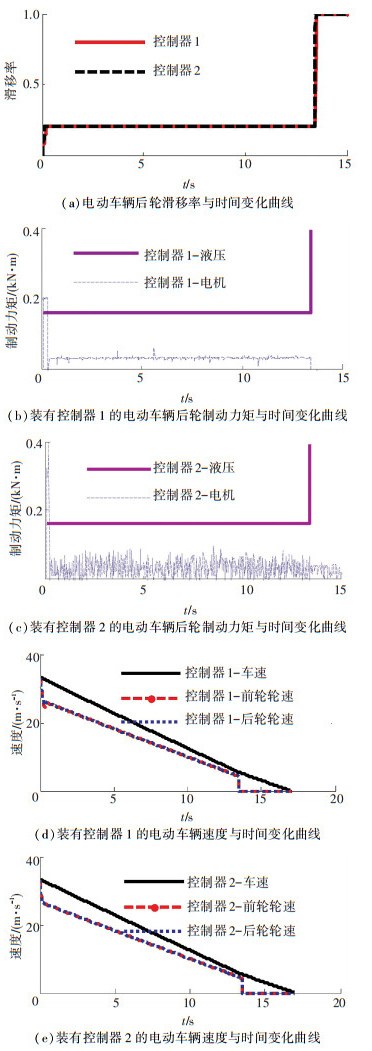
4.1 低附路面行驶时的防抱死性能选取μ(λ)=0.2的冰雪路面作为低附路面行驶工况,图 4为电动车辆在低附着路面行驶工况下实施防抱死控制时的制动性能.
|
图 4 低附路面工况下紧急制动时的制动性能 Figure 4 Braking performances under low adhesion ground condition |
图 4(a)可见,车辆在低附路面上实施防抱死控制的过程中,控制器1和控制器2都能精准地追踪理想滑移率;制动过程快要结束时前、后车轮出现抱死,但是电动车辆的实时车速已经很低,车轮的抱死并不会影响到电动车辆的制动安全;图 4(b)~4(c)显示,电动车辆在低附路面上紧急制动时,液压制动系统提供基础制动力矩,通过改变电机制动力矩大小实现理想滑移率的追踪,装有控制器1的车辆的电机制动力矩波动幅度要小于装有控制器2的车辆;从图 4(d)~4(e)看出,整个制动过程中装有控制器1和控制器2的电动车辆的防抱死过程都大约持续了13.5 s,两者的前、后轮轮速都能较好地跟随车速下降而下降,充分发挥了轮毂电机响应迅速,控制精确高的优势,取得了良好的控制效果.
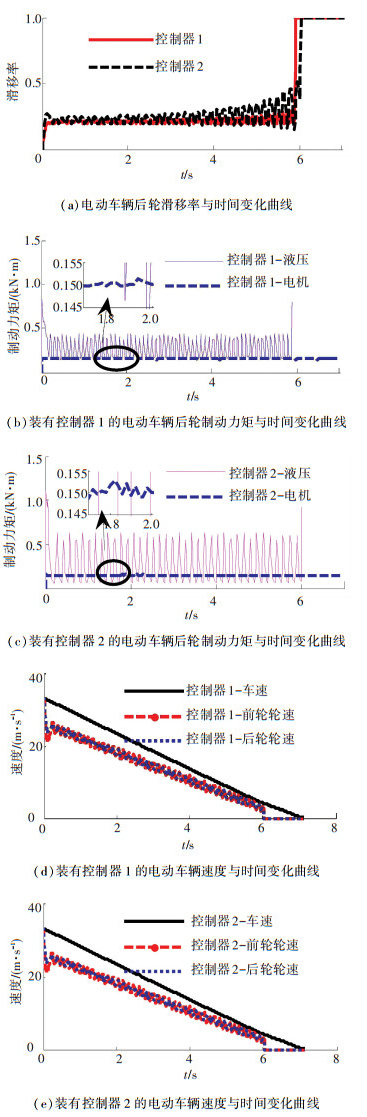
4.2 中附路面行驶时的防抱死性能选取μ(λ)=0.5的湿滑沥青路面作为中附路面行驶工况,图 5为电动车辆在中附路面行驶工况下实施防抱死控制时的制动性能.
|
图 5 中附路面工况下紧急制动时的制动性能 Figure 5 Braking performances under middle adhesion ground condition |
图 5(a)可见,车辆在中附路面上实施防抱死控制的过程中,采用控制器1和控制器2的电动车辆的后轮滑移率均保持在0.2左右,滑移率均方根误差值分别为1.04×10-2和9.50×10-2,且前者较后者下降了89.1%,说明基于改进线性二次型最优控制算法关于追踪理想滑移率方面能够取得较为优越的控制效果. 图 5(b)~5(c)显示,电动车辆在中附路面上紧急制动时,轮毂电机提供基础制动力矩,通过改变液压制动力矩实现理想滑移率的追踪.由图 5(d)~5(e)可见,在中附路面行驶工况下,虽然采用控制器1和控制器2的车辆前、后轮轮速都可以和车速保持接近,但是前者的前、后轮轮速波动程度要明显小于后者;此外,控制器1的防抱死持续时间为5.9 s,相比与控制器2缩短了0.1 s,说明了在中附路面工况下,采用控制器1的电动车辆相比于采用控制器2的电动车辆来说能够更为有效地缩短电动车辆的制动距离.
4.3 高附路面行驶时的防抱死性能选取μ(λ)=0.8的干燥沥青路面作为高附路面行驶工况,图 6为电动车辆在高附路面行驶工况下实施防抱死控制时的制动性能.

|
图 6 高附路面工况下紧急制动时的制动性能 Figure 6 Braking performances under high adhesion ground condition |
图 6(a)可见,车辆在高附路面上实施防抱死控制的过程中,安装有控制器1和控制器2的电动车辆的滑移率均方根误差值分别为1.48×10-2和7.01×10-2,前者的较后者下降了78.9%,说明基于改进线性二次型最优控制算法的控制器1在高附着系数路面行驶工况下可以获得更为优越的滑移率控制效果;另外在制动末尾阶段,当电动车辆的实际车速低于15 km/h时退出防抱死控制,前、后电动轮滑移率迅速上升到100%. 图 6(b)~6(c)显示,电动车辆在高附路面下紧急制动时,轮毂电机不参与ABS工作,液压制动系统单独完成防抱死控制;且装有控制器1的车辆的电机制动力矩波动幅度要小于装有控制器2的车辆;图 6(d)~6(e)可见,在高附着系数路面行驶工况下,虽然采用控制器1和控制器2的电动车辆并没有发生前、后轮抱死的情况,但是采用控制器2的电动车辆防抱死控制过程中前、后轮轮速的波动程度较大,而采用控制器1的电动车辆防抱死控制过程中前、后轮轮速的变化趋势仍然能较好地跟随车速变化;且控制器1的防抱死过程持续了3.75 s,相比与控制器2的防抱死全程的3.88 s,缩短了0.13 s,说明了随着路面附着系数的提高,基于改进线性二次型最优控制算法的控制器在电动汽车防抱死控制过程中的有效性就越明显.
5 结论1) 通过构造虚拟阻尼量以及无穷小量来建立黎卡提方程的方法,提出一种改进线性二次型最优控制控制算法,该方法能够克服现有线性二次型最优控制算法无法应用于车辆防抱死控制的缺陷,并据此成功地设计出了电动车辆ABS控制器.
2) 在低附着路面行驶工况下,安装有改进线性二次型最优防抱死控制器的电动汽车能够充分发挥轮毂电机响应迅速以及防抱死精确度高的优势.
3) 在中、高附着路面行驶工况下,装有改进线性二次型最优防抱死控制器的车辆的车轮实际滑移率虽然会出现轻微的波动,但是能够迅速地回到稳态值;且安装有该控制器的电动汽车的滑移率均方根误差值相比于安装有滑模防抱死控制器的电动汽车分别下降了89.1%和78.9%,说明相比较滑模控制算法,本文所提出的改进线性二次型最优控制算法能够实现更为精确的车轮滑移率控制效果.
| [1] |
PEEIE M, OGINO H, OSHINOYA Y. Skid control of a small electric vehicle with two in-wheel motors: simulation model of ABS and regenerative brake control[J]. International Journal of Crashworthiness, 2016, 21(5): 396. DOI:10.1080/13588265.2016.1147731 |
| [2] |
陈涛, 刘荣昌, 杨震. 交通事故再现中轮胎/路面附着系数估算方法[J]. 江苏大学学报(自然科学版), 2015, 36(4): 386. CHEN Tao, LIU Rongchang, YANG Zhen. Estimate method of tire-road friction coefficient in accident reconstruction[J]. Journal of Jiangsu University (Natural Science Edition), 2015, 36(4): 386. DOI:10.3969/j.issn.1671-7775.2015.04.003 |
| [3] |
刘志远, 井后华, 陈虹. 一种汽车防抱死制动系统的非线性控制方法[J]. 哈尔滨工业大学学报, 2012, 44(5): 7. LIU Zhiyuan, JING Houhua, CHEN Hong. Nonlinear control method for automotive anti-lock braking system[J]. Journal of Harbin Institute of Technology, 2012, 44(5): 7. DOI:10.3969/j.issn.1009-1971.2012.05.003 |
| [4] |
PENG D, ZHANG Y, YIN C L, et al. Combined control of a regenerative braking and anti-lock braking system for hybrid electric vehicles[J]. International Journal of Automotive Technology, 2008, 9(6): 749. DOI:10.1007/s12239-008-0089-3 |
| [5] |
CHIANG W, YIN D, SHIMIZU H. Slip-based regenerative ABS control for in-wheel-motor drive EV[J]. Journal of the Chinese Institute of Engineers, 2015, 38(2): 220. DOI:10.1080/02533839.2014.955974 |
| [6] |
王国业, 刘昭度, 胡仁喜, 等. 基于等效滑移率变化的汽车防抱死制动系统模糊直接自适应控制[J]. 机械工程学报, 2008, 41(11): 242. WANG Guoye, LIU Zhaodu, HU Renxi, et al. Fuzzy logic direct adaptive control of ABS-equipped vehicles based on equivalent slip differential of tire[J]. Chinese Journal of Mechanical Engineering, 2008, 41(11): 242. |
| [7] |
赵国柱, 腾建辉, 魏民祥, 等. 基于模糊控制的电动汽车低速再生ABS研究[J]. 中国机械工程, 2012, 23(1): 117. ZHAO Guozhu, TENG Jianhui, WEI Minxiang, et al. Study on low-speed regenerative braking of electric vehicle as ABS based on fuzzy control[J]. China Mechanical Engineering, 2012, 23(1): 117. DOI:10.3969/j.issn.1004-132X.2012.01.026 |
| [8] |
孙大许, 兰凤崇, 何幸福, 等. 双电机四驱电动汽车自适应复合防抱死控制[J]. 吉林大学学报(工学版), 2016, 46(5): 1405. SUN Daxu, LAN Fengchong, HE Xingfu, et al. Self-adaptive composite ABS of dual-motor four-wheel drive electric vehicle[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(5): 1405. |
| [9] |
WU M C, SHIH M C. Hydraulic anti-lock braking control using the hybrid sliding-mode pulse width modulation pressure control method[J]. Proceedings of the Institution of Mechanical Engineers. part Ⅰ: Journal of Systems and Control Engineering, 2001, 215(2): 177. DOI:10.1243/0954408011530334 |
| [10] |
ZHANG X W, XU Y, PAN M, et al. A vehicle ABS adaptive sliding-mode control algorithm based on the vehicle velocity estimation and tire/road friction coefficient estimations[J]. Vehicle System Dynamics, 2014, 52(4): 475. DOI:10.1080/00423114.2013.864775 |
| [11] |
刘学军, 何仁. 电磁-液压复合防抱死制动系统滑模控制[J]. 农业机械学报, 2014, 45(5): 1. LIU Xuejun, HE Ren. Sliding mode control in electromagnetic-hydraulic hybrid anti-lock braking system[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(5): 1. |
| [12] |
BASIN M, RODRIGUEZ-RAMIREZ P, FERRARA A, et al. Sliding mode optimal control for linear systems[J]. Journal of the Franklin Institute, 2012, 349(4): 1350. DOI:10.1016/j.jfranklin.2011.05.010 |
| [13] |
IGNACIUK P, BARTOSZEWICZ A. LQ optimal sliding-mode supply policy for periodic-review perishable inventory systems[J]. Journal of the Franklin Institute, 2012, 349(4): 1561. DOI:10.1016/j.jfranklin.2011.04.003 |
| [14] |
张露, 王国业, 张延立, 等. 电动汽车再生摩擦集成制动系统ABS控制性能研究[J]. 农业机械学报, 2015, 46(10): 350. ZHANG Lu, WANG Guoye, ZHANG Yanli, et al. ABS control performance of integrated brake system with regenerative friction brake in electric vehicle[J]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(10): 350. DOI:10.6041/j.issn.1000-1298.2015.10.047 |
| [15] |
WU M C, SHIH M C. Simulated and experimental study of hydraulic anti-lock braking system using sliding-mode PWM control[J]. Mechatronics, 2003, 13(4): 331. DOI:10.1016/S0957-4158(01)00049-6 |
| [16] |
张雷, 于良耀, 宋健, 等. 电动汽车再生制动与液压制动防抱死协调控制[J]. 清华大学学报(工学版), 2016, 56(2): 152. ZHANG Lei, YU Liangyao, SONG Jian, et al. Coordinated anti-lock braking control of regenerative and hydraulic braking systems in electric vehicles[J]. Journal of Tsinghua University (Science and Technology), 2016, 56(2): 152. |
 2018, Vol. 50
2018, Vol. 50


