随着自动化工厂的普及,机器视觉技术广泛用于工业生产,进行零件的识别和检测.然而,由于受到传送带速度变化或曝光不足的影响,得到的图像可能会产生运动模糊,影响检测效果,因此需要对图像去模糊[1].根据模糊核即点扩散函数(PSF)是否已知,去模糊方法可分为非盲复原和盲复原两类[2-4].前者的PSF已知,仅需进行图像复原;而后者需要估计PSF并恢复出清晰的图像.无论是估计PSF还是去模糊,从单张运动模糊的照片中恢复出清晰的图像,都是数字图像处理的重要课题[5].
针对图像去运动模糊,国内外有大量的相关研究.如经典的维纳滤波[6],它通过计算最小方差来恢复图像;常用的Richardson-Lucy反卷积[7],假定自然图像的像素服从柏松分布,通过迭代求解.文献[8]用一种基于偏微分方程PDE的方法恢复自然图像,通过结合抗反射边界条件和再次模糊的步骤,减弱了振铃效应.文献[9]根据二维模糊图像的模糊路径进行离散化,估计PSF并进行恢复.文献[10]采用自然图像的导数稀疏作为约束,在反卷积过程中力图减少人工振铃效应.文献[5]分析了噪声对恢复效果的影响,建立了噪声在空域的概率模型,在估计和恢复之间迭代,得到准确的模糊核,最后引入局部平滑映射抑制伪影,得到良好的复原结果.文献[11]认为PSF估计不应依赖于强边缘,因而提出一种新的量度来选择边缘,进而初步评估PSF核,然后使用基于空间先验和迭代支持检测(ISD)的方法优化PSF,最后使用TV-1反卷积模型来抑制噪声,得到了优秀的去噪结果.由于大部分方法都假定模糊核没有误差和噪声,所以对PSF的估计误差和图像采集过程中引入的噪声都会产生明显的振铃效应[5],在工业检测中会引发误检.同时很多效果良好的方法往往需要多次迭代,繁重的计算使在生产线上进行实时去模糊变得困难.针对上述问题,本文提出一种快速去除匀速直线运动模糊的方法,该方法可以快速评估模糊核并进行图像复原.在恢复工业检测中关心的清晰形状边缘和运算速度两方面表现良好,并且不需要额外的硬件.
1 匀速直线运动的模糊核估计 1.1 匀速直线运动物体的模糊核当相机曝光时,运动的被测物会在CCD上产生拖影,运动的方向和距离决定了模糊核(PSF)的大小.根据线性系统理论,图像的模糊模型为
| $ \mathit{\boldsymbol{I}} = \mathit{\boldsymbol{L}} \otimes P + n. $ | (1) |
其中:I为模糊的图像矩阵,L为原图像矩阵,n为加性噪声,P为线性时不变点扩散函数PSF.对于匀速直线运动模糊,P(x)的表达式为
| $ P\left( x \right) = \left\{ \begin{array}{l} \frac{1}{N}, \;\;\;\;0 \le x \le N - 1;\\ 0, \;\;\;\;\;\;\;其他. \end{array} \right. $ | (2) |
其中N为位移的大小.
1.2 模糊核估计 1.2.1 运动方向估计运动模糊角度的估计可以通过分析图像的频谱得到.由傅里叶变换可知,沿着x轴运动的匀速直线运动模糊的频域表达式为
| $ \begin{array}{l} H\left( {u, v} \right) = \int_0^T {\exp \left[ { - {\rm{j}}2{\rm{ \mathit{ π} }}{x_0}\left( t \right)} \right]{\rm{d}}t} = \\ \;\;\;\;\;\;\;\;\int_0^T {\exp \left[ { - {\rm{j}}2{\rm{ \mathit{ π} }}uat/T} \right]{\rm{d}}t} = \\ \;\;\;\;\;\;\;\;T\sin \left( {{\rm{ \mathit{ π} }}ua} \right)\exp \left( { - {\rm{j \mathit{ π} }}ua} \right)/\left( {{\rm{ \mathit{ π} }}ua} \right). \end{array} $ | (3) |
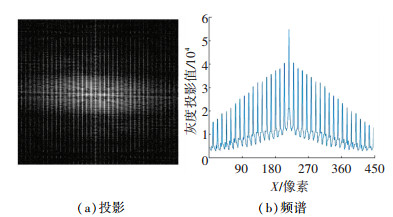
由于H(u, v)在u=n/a处为零,所以其频谱会产生周期性的条纹,其在θ方向的投影会产生一系列局部极值,条纹的法向向量指向物体的运动方向,如图 1所示.
|
图 1 模糊图像的频谱图及其投影 Figure 1 Spectrum of blurrd image and its projection |
通过常用的Radon变换可以检测该方向[12].该变换在极坐标中进行,需要对0°~180°各个方向进行Radon变换.因为工业检测中的物体运动方向通常已知,所以无需遍历整个角度空间,仅需适当放宽检测范围即可确定其精确角度.例如已知传送带上物体运动方向为90°,则根据运动误差适当放宽检测范围,如90°±1°即可,这将显著缩短检测时间.
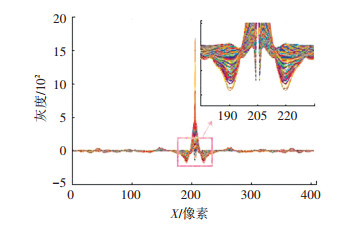
1.2.2 模糊核尺寸估计得到模糊方向后,将图像旋转到模糊方向与X轴平行,然后使用微分自相关方法[13]进行模糊核尺寸估计,其尺度估计曲线如图 2所示,其最小值之间距的一半即为模糊核长度.对于图中的情况,两个次小峰的距离为30像素,则相应的PSF为长15,值为0.047 6的一维向量.
|
图 2 PSF尺度估计曲线 Figure 2 PSF scale estimation curve |
Richardson-Lucy法[13]假设成像服从分布:
| $ I\left( i \right) = \sum {P\left( {i\left| j \right.} \right)O\left( j \right)} . $ | (4) |
式中I为模糊图像,O为原图像,P(i|j)为点扩散函数.观察计数D(i)和期望计数I(i)的联合概率分布为
| $ \begin{array}{l} P\left( {D/O} \right) = P\left( {D/I = P \times O} \right) = \prod\limits_{r \in S} {\exp \left\{ { - \left( {P \times O} \right)} \right\}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{{\left[ {\left( {P \times O} \right)} \right]}^D}}}{{D!}}. \end{array} $ | (5) |
可以得到迭代公式
| $ {O_{{\rm{new}}}}\left( j \right) = O\left( j \right)\frac{{\sum\limits_i {P\left( {i\left| j \right.} \right)D\left( i \right)} }}{{\sum\limits_i {P\left( {i\left| j \right.} \right)I\left( i \right)} }}. $ | (6) |
R-L算法采用最大似然法进行估计,执行速度较快.但因为对原图的噪声估计并不精确,因此恢复的图像会产生明显的振铃.在物体边缘处产生的伪影会影响尺寸的测量,并被检测程序误认为是缺陷,从而产生误检.
2.2 引导滤波引导滤波是近年提出的一种同时考虑空间差异和亮度差异的滤波[14].它利用引导图像的结构特征,对输入图像进行滤波.滤波后的图像在保留了输入的图像的整体特征的同时,又表征了引导图像的结构变化[15-17].
引导滤波假设输入图像和引导图像在局部范围内存在线性关系.设输入图像为p,输出图像为q,引导图为I,则在以k为中心的窗口wk中有
| $ {q_i} = {a_k}{I_i} + {b_k}, \forall i \in {w_k}. $ | (7) |
为确定系数,可转化为最优化问题:
| $ E\left( {{a_k}, {b_k}} \right) = \sum\limits_{i \in {w_k}} {\left( {{{\left( {{a_k}{I_i} + {b_k} - {P_i}} \right)}^2} + \varepsilon a_k^2} \right)} . $ | (8) |
其中Pi为要处理的图像,参数ε为了防止ak过大.该式可以利用线性回归求解,即
| $ {a_k} = \frac{{\frac{1}{{\left| w \right|}}\sum\nolimits_{i \in {w_k}} {{I_i}{p_i} - {\mu _k}{{\bar p}_k}} }}{{\sigma _k^2 + \varepsilon }}, $ | (9) |
| $ {b_k} = {{\bar p}_k} - {a_k}{\mu _k}. $ | (10) |
式中
对式(7)两侧取梯度可以得到▽qi=ak▽I,也就是只有在引导图存在边缘的位置,q才会存在边缘.这使得引导滤波在平滑图像的同时具有边缘保持特性.系数a决定了边缘保持的强度.当a较大时,输出的梯度值也较大,物体的边缘更清楚;当a较小时,输出的梯度值变小,物体的边缘也变得更平滑.
2.3 基于R-L引导滤波的去模糊R-L方法去模糊后会产生振铃,这是一种在模糊图中并不存在的梯度变化,因此可以利用引导滤波的梯度同步特性进行抑制.然后,结合梯度信息融合滤波前后的两幅图像,得到边缘清晰,振铃效应减弱的去模糊图.设模糊图像为I,W为R-L滤波,G为引导滤波, 则恢复图像L为
| $ L = \tau W\left( I \right) + \left( {1 - \tau } \right)G\left( {I, W\left( I \right), \kappa } \right). $ | (11) |
使用模糊图像I作为引导图像,κ为滑动窗口大小.这里引导滤波使用MATLAB提供的imguidedfilter函数计算,其中两个主要参数neighborhoodsize和degreeofsmoothing,分别表示引导滤波的窗口大小和平滑力度.实验表明,窗口大小设为PSF的尺寸,平滑力度设为0.16时,能在抑制振铃和保持边缘之间取得最好的平衡. τ为引导图在去模糊图像中的权重,可表示为
| $ \tau = {\mathop{\rm sgn}} \left( {\left| {{\nabla _{{\rm{axis}}}}I} \right| + \xi } \right). $ | (12) |
其中▽axisI为图像在运动方向的梯度;ξ为一小数,使符号函数不为零.当像素位于边缘时,τ较大,输出值中R-L去模糊的权重大;而在较为平滑的位置,τ较小,输出值中引导滤波后的权重大.这里使用符号函数而不是高斯或Sigmoid这类平滑函数的原因是为了保持边缘的清晰.
为验证提出方法法的有效性,获取一副金属条纹的工件图,通过MATLAB仿真得到运动模糊图像,然后使用第1节的方法估计模糊角度和模糊尺寸,并用提出的方法恢复图像.如图 3所示,3(a)和3(d)为移动方向为90°,模糊核大小分别为5像素和10像素的图片,图 3(b)和3(e)为R-L滤波的结果,图 3(c)和3(f)为提出的方法得到的结果.由图可见,R-L滤波在线条边缘内外产生了扩散的伪影,而本文提出的方法几乎没有伪影产生.为测量去除模糊对尺寸测量的影响,测试了去模糊前后工件的线宽,结果见表 1.可见,提出的方法较好的恢复出了边缘,对尺寸测量的影响较小.

|
图 3 模糊图像及复原结果 Figure 3 Blurred images and deblurred results |
| 表 1 线宽测量结果 Table 1 Line width size measurement results |
通过运动模糊仿真,可以在参数可控的条件下考察算法性能.使用方向为90°,长度为15个像素的矢量作为模糊核处理一副实际拍摄的工件图片得到仿真图像.接着添加均值0.005,方差0.000 1的高斯噪声得到另一幅加噪的仿真图像.分别使用HQ Motion Deblur[5](HQ)、two-phase kernel estimation for robust motion Deblur[14] (TPKE)和提出的算法对仿真图像进行去模糊.
需要说明的是,虽然前两种方法都包括PSF估计和去模糊两部分,但通过仔细的调参表明,其对匀速直线运动的PSF评价较第1节中给出的方法有更多误差.如图 4所示,图 4(a)为运动模糊使用的模糊核及HQ方法评估得到的模糊核.真是模糊核尺寸为15个像素,方向为90°. 图 4(b)为提出的方法的估计和TPKE方法评估得到的模糊核.因为HQ和TPKE两种方法需要输入PSF核的高和宽作为估计范围,因此使用高为15像素,宽分别为15、5、3和1像素作为参数进行估计.可以看到,当给出的宽度较大时,这两种方法都在与运动方向成45°角的范围内产生了错误的估计;当宽度逐渐缩小时,在水平方向的评估误差仍然存在;指定宽度为1时,估计误差才会接近真值.因此这里使用第1节中方法得到的模糊核尺寸作为后两者的模糊核评估参数.

|
图 4 三种方法的PSF评价 Figure 4 PSF evaluation of 3 methods |
仿真图像和恢复结果如图 5所示.可见,因为有匀速直线的先验信息,提出的方法得到了准确的PSF.而其他两种方法仅有直线运动的先验,而不知道速度,因此产生了误差,由图可见,基于高斯分布的假设使两者的PSF都有平滑的倾向.相比之下,因为更准确的细节梯度图和ISD迭代优化[14],TPKE得到的PSF的方差更小,接近真值.

|
图 5 仿真模糊图像及复原结果 Figure 5 Simulation of blurred images and restoration results |
当图像没有噪声时,因为HQ方法对PSF估计误差稍大,因此恢复的图像在线条边缘处产生了较多的振铃.而TPKE恢复的结果良好,比提出的方法产生了稍多的伪影,但边缘更为锐利.当图像引入了轻微的噪声时,提出方法的优势开始显现.如图,HQ方法产生了更多的振铃;TPKE法依靠L1全变分作为约束,在图像大部分区域消除了噪音的影响,但在图像的上边缘处仍然产生了振铃;而提出的方法依靠梯度平滑约束,抑制了几乎所有的伪影.
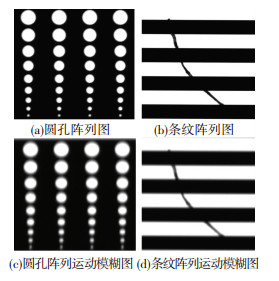
3.2 实验在实际检测环境中,工件运动速度和方向的抖动、拍摄平台的扰动等都与相对理想的仿真环境不同,因此需要通过实验来检测算法在实际应用中的效果.实验平台如图 6所示,相机为JAI_BM-500GE,快门时间设置为10 ms;镜头为4倍远心镜头MML-HR4;工件放置在镜头下方的承片台上,可沿Y轴方向以某个速度运动.实验中使用的样件有两种,一种为由大到小排列的圆孔,另一种是被纤维污染的直线阵列,两者的位移速度分别为2、4 mm/s,清晰的图像和获取的模糊图像如图 7所示.

|
图 6 实验平台 Figure 6 Experiment platform |
|
图 7 采集的模糊的图像 Figure 7 Acquired blurred images |
通过1.1节的算法可得两幅图像的模糊方向为90°,模糊核大小分别为15像素和21像素.分别使用HQ Motion Deblur[5] (HQ)、Two-Phase Kernel Estimation for Robust Motion Deblur[14] (TPKE)和提出的算法进行去模糊. 3种方法得到的去模糊图像如图 8所示, 其中图 8(a)~8(c)分别为3种算法对圆孔图像的恢复结果,图 8(e)~8(f)为对直线阵列的恢复结果.为便于观察,在每幅图像中选取两部分放大,列于图像右侧.接着,通过客观评价指标、去模糊前后对尺寸测量的影响和运行速度三方面进行效果评价.

|
图 8 HQ Motion Deblur、TPKE for Robust Motion Deblur和本文提出的算法的复原图像 Figure 8 Comparison of deblurred images by HQ Motion Deblur, TPKE for Robust Motion Deblur and the proposed algorithm |
首先,使用客观评价指标PSNR和SSIM比较不同算法恢复图像的效果.
1) 峰值信噪比RPSNR是常用的衡量图像失真的指标,值越大表明图像质量越好.其计算公式为
| $ {R_{{\rm{PSNR}}}} = 10\lg {\left( {255} \right)^2}/{R_{{\rm{MSE}}}}, $ | (13) |
| $ {R_{{\rm{MSE}}}} = \frac{1}{{M \times N}}\sum\nolimits_{x = 1}^M {\sum\nolimits_{y = 1}^N {f\left( {x, y} \right) - \hat f\left( {x, y} \right)} } , $ | (14) |
式中RMSE为图像的均方误差.
2) 结构相似度RSSIM用来衡量图像结构的完整性,是常用的图像质量评价方法,值越接近1越好.其值通过滑动高斯窗口对图像分块,并用高斯加权计算每个窗口的均值、方差和协方差得到.每个块的RSSIM计算公式为
| $ {R_{{\rm{SSIM}}}}\left( {x, y} \right) = \frac{{\left( {2{\mu _x}{\mu _y} + {C_1}} \right)\left( {2{\sigma _{xy}} + {C_2}} \right)}}{{\left( {\mu _x^2 + \mu _y^2 + {C_2}} \right)\left( {\sigma _x^2 + \sigma _y^2 + {C_2}} \right)}}. $ | (15) |
各参数值的选取见文献[18].本文使用MATLAB提供的SIMM函数的默认参数进行计算.
RPSNR和RSSIM都需要比较变化前后的两幅图像,这里的静止图像是通过反复移动位移台,利用透明贴图与模糊图像进行匹配得到.计算所得的RPSNR和RSSIM见表 2.要注意的是,由于清晰和模糊这两幅图像无法同时拍摄,因此其对应的被测区域无法完全一致,所以这里RPSNR和RSSIM并非绝对量度,而是用来衡量不同算法的恢复效果.
| 表 2 恢复图像的RPSNR和RSSIM Table 2 The RPSNR and RSSIM of deblurred images |
从表 2可以看出,提出方法的RPSNR和RSSIM值都优于HQ和TPKE方法.这里的差异主要来自振铃效应.对于圆孔图像,如图 8(a)~8(c)所示,HQ和TPKE方法在整幅图的上边缘和圆孔内部都产生了振铃,尤以内部最为明显. HQ方法恢复图像的边缘较锐利,但伪影也更明晰;当圆孔较小的时候,伪影占据了相当大的面积,这会给尺寸测量带来困扰,在稍后的实验也会看到这点.而提出的算法几乎没有产生任何振铃效应,圆孔内部亮度均匀一致,且边缘较为清晰,整体效果与原图最接近. 图 8(d)~8(f)是沾染纤维污物的直线阵列的恢复结果,可以评估去模糊图像对污染物检测的影响.如图,HQ和TPKE在物体边缘处产生了振铃,明暗相间的条纹充斥了整张图片,这些条纹很可能会被缺陷检测算法判断为划痕. HQ算法依然保持锐利的边缘和清晰的伪影,纤维污物四周的振铃可能会让缺陷检测算法扩大检测的范围,或将纤维认作划痕. TPKE方法边缘稍显模糊,伪影也少一些.提出的算法几乎没有产生任何振铃,污物的边界完整清楚,易于识别.
3.4 尺寸和坐标测量评价因为工业图像经常用于工件的检测和定位,故选取圆孔图像的第一列,分析其直径和坐标在去模糊前后的变化.如图 9所示,直方图为圆孔直径,折线图为相对误差;横坐标为圆孔标号(由大到小).可见,当圆孔较大时,3种方法的差异很小,与实际值十分接近,相对误差在1%附近波动.当圆孔直径缩小到15个像素左右时(序号8),由于HQ和TPKE方法产生的伪影占据圆孔的空间变得十分可观,影响到了二值化过程,所以检测误差迅速增大到6%和3%,而提出的方法的误差没有变化,仍小于1%.当圆孔直径继续减小到8个像素时,提出算法的误差才开始变大,但仍小于其他两种方法.

|
图 9 圆孔恢复图的直径测量结果 Figure 9 The diameter of the circular hole deblurred images |
去模糊图对圆心坐标测量的影响,分析结果如图 10所示.因为图像位移方向为90°,所以X坐标全程变化不大.当圆孔较大时,3种方法测得的Y坐标误差都小于0.3像素;当圆孔减小到8个像素(序号9)时,HQ和TPKE方法恢复图的测量误差分别为0.8像素和0.51像素;而得益于良好的振铃抑制,提出算法恢复图的误差仍然较小,为0.31像素.

|
图 10 圆孔恢复图的圆心测量误差 Figure 10 The center measurement error of the circular hole deblurred images |
由上可见,在大尺度的图形上,提出算法恢复图像的测量精度与另外两种算法差别不大;而在小尺度图形上,提出的算法具有优势,满足工业测量所需要的稳定性.模糊图及复原结果如图 11所示.

|
图 11 Lena模糊图及复原结果 Figure 11 Blurred "Lena" and the recovery result |
工业检测中通常需要实时处理,对算法的执行时间较为敏感.为评估运算速度,在i7-6700平台,8 G内存,使用GPU加速的计算机上,使用HQ、TPKE和提出的方法恢复大小为800像素×600像素,8位色深的5幅模糊程度不同的灰度图片,耗时见表 3.相比基于迭代的两种方法,提出的算法耗时较少,优势明显,经过优化后可以做到实时处理.
| 表 3 3种方法的运算时间 Table 3 The running time of the 3 methods |
1) 面向工业检测,提出了结合R-L滤波和引导滤波的运动图像去模糊方法,在保持工件清晰边缘的同时,去除振铃效应带来的伪影.实验结果表明,在客观评价指标、对尺寸测量的影响和运算速度方面,提出的方法具有优势.
2) 为了提高速度,提出算法的去模糊部分使用了R-L滤波.如果对实时性无要求,或硬件计算能力强大,去模糊算法可以改为其他运算繁重但效果更好的算法,然后使用本方法的后续部分去除振铃模糊.在前述实验的直线阵列图像中,将R-L滤波改为HQ算法,RPSNR可从18.89提高到25.07,RSSIM从63.3%提高到80.84%.
3) 除工业检测外,本方法对纹理复杂的自然图像的恢复效果显著,可见,本方法对图像平缓区域附近的振铃抑制效果很好,缺点是在强边缘处引入了噪声,例如人物鼻子附近的斑点,这需要在今后的工作中进一步研究解决.
| [1] |
RAJAGOPALAN A N, CHELLAPPAR. Motion deblurring: algorithms and systems[M]. Cambridge: Cambridge University Press, 2014: 12.
|
| [2] |
TIWARI S, SHUKLA V P, SINGH A K. Review of motion blur estimation techniques[J]. Journal of Image and Graphics, 2013, 1(4): 176. |
| [3] |
RUIZ P, ZHOU Xu, MATEOS J, et al. Variational bayesian blind image deconvolution: A review[J]. Digital Signal Processing, 2015, 47: 116. DOI:10.1016/j.dsp.2015.04.012 |
| [4] |
SCHMIDT U, ROTHER C, NOWOZIN S, et al.. Discriminative non-blind deblurring[C]//CVPR. Portland: IEEE Computer Society, 2013
|
| [5] |
SHAN Qi, JIA J, AGARWALA A. High-quality motion deblurring from a single image[C]//California: Acm transactions on graphics (tog), 2008, 27(3): 73
|
| [6] |
WIENERN. Extrapolation, interpolation, and smoothing of stationary time series[M]. Cambridge, MA: MIT Press, 1949.
|
| [7] |
RICHARDSON W H. Bayesian-based iterative method of image restoration[J]. Journal of Astronomy, 1974, 79: 745. DOI:10.1086/111605 |
| [8] |
DONATELLI M, ESTATICO C, MARTINELLI A. Improved image deblurring with anti-reflective boundary conditions and re-blurring[J]. Inverse Problems, 2006, 22(6): 2035. DOI:10.1088/0266-5611/22/6/008 |
| [9] |
刘微.运动模糊图像恢复算法的研究与实现[D].长春: 中国科学院长春光学精密机械与物理研究所, 2005 Liu Wei. Research and Implementation of Motion Blur Image Restoration Algorithm[D].Changchun: Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, 2005 |
| [10] |
LEVIN A, FERGUS R, DURAND R, et al. Image and depth from a conventional camera with a coded aperture[J]. ACM Transactions on Graphics, 2007, 26(3): 70. DOI:10.1145/1276377 |
| [11] |
XU L, JIA J. Two-phase kernel Estimation for robust motion deblurring[C]//European Conference on Computer Vision. Berlin Heidelberg: Springer, 2010: 157
|
| [12] |
MOGHADDAM M E. JAMZAD M. Finding point spread function of motion blur using radon transformation and modeling the motion length[C]//Proceedings of the Fourth IEEE International Symposium on Signal Processing and Information Technology.Rome: IEEE, 2004: 314
|
| [13] |
RICHARDSON W H. Bayesian-based iterative method of image restoration[J]. Journal of optical society of America, 1972. |
| [14] |
YITZHAKY Y, KOPEIKA N S. Identification of blur parameters from motion blurred images[J]. Graphical Models and Image Processing, 1997, 59(5): 310. DOI:10.1006/gmip.1997.0435 |
| [15] |
HE K, SUN J, TANG X. Guided image filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1397. DOI:10.1109/TPAMI.2012.213 |
| [16] |
谢伟, 周玉钦, 游敏. 融合梯度信息的改进引导滤波[J]. 中国图象图形学报, 2016, 21(9): 1119. XIE Wei, Zhou Yuqin, You Min. Improved guided filtering with fusion gradient information[J]. Chinese Journal of Image and Graphics, 2016, 21(9): 1119. |
| [17] |
曹伟, 王华彬, 石军, 等. 基于边缘检测加权引导滤波的指静脉图像增强算法[J]. 激光与光电子学进展, 2017, 54(2): 166. CAO wei, WANG huabin, SHI Jun, et al. Finger vein image enhancement algorithm based on edge detection weighted guided filter[J]. Progress in Laser and Optoelectronics, 2017, 54(2): 166. |
| [18] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600. DOI:10.1109/TIP.2003.819861 |
 2018, Vol. 50
2018, Vol. 50


