2. 哈尔滨工业大学 控制与仿真中心,哈尔滨 150001;
3. 智能感知与先进控制国家民委重点实验室(大连民族大学),辽宁 大连 116600;
4. 大连理工大学 土木工程博士后流动站,辽宁 大连 116024;
5. 大连葆光节能空调设备厂, 辽宁 大连 116000
2. Control and Simulation Centre, Harbin Institute of Technology, Harbin 150001, China;
3. Key Lab of Intelligent Perception and Advanced Control(Dalian Minzu University), Dalian 116600, Liaoning, China;
4. Center for Post-doctoral Studies of Civil Engineering, Dalian Institute of Technology, Dalian 116024, Liaoning, China;
5. Dalian Baoguang Energy Saving Air Conditioning Corporation, Dalian 116600, Liaoning, China
被动跟踪任务常常可归结为某种非线性估计问题[1].扩展卡尔曼滤波器(extended Kalman filter, EKF)算法结构简单且易于实现,过去几十年中经常用于解决非线性估计问题[2-5].然而,EKF仅采用一阶泰勒展开逼近非线性函数,且在计算状态变量的后验概率分布时忽略了先验变量的随机特征,因此在初始估计精度不高或系统模型非线性度较高时常难以收敛[5].目前针对EKF有众多改进方法,如迭代扩展卡尔曼滤波(IEKF)[5-6]、高阶EKF[7]等. IEKF的本质是在测量更新步骤,采用迭代算法改善线性化参考点的选取方式,虽然有部分文献研究表明,某些情况下IEKF的表现要优于EKF,但目前为止尚无理论性的研究成果能够确保IEKF的优越性[8-10].高阶EKF的设计思路是采用更高阶的泰勒级数逼近非线性函数,理论上这种算法的估计效果要好于EKF,但高阶展开项的引入在很大程度上增大了算法计算量,进而抑制了其在实际问题中的应用[11]. EKF的另一大类改进方法称为虚拟噪声技术[12].虚拟噪声技术认为,非线性系统的线性化误差在一定程度上可以归结为某种统计特性未知的噪声,因而如果能够采用某种自适应滤波技术,在线估计虚拟噪声的统计特性,就可以降低线性化误差,提高估计精度.
2005年以来,一类基于采样点技术设计的非线性滤波器得到了学者的普遍关注.对于非高斯型变量,逼近精度可以达到二阶,对于高斯型变量能达到三阶.此外,这类算法不需计算偏微分,因而作为传统算法的替代,在许多领域得到了应用[9-11, 13].这类方法中有代表性的两种分别称为无迹卡尔曼滤波(unscented Kalman filter,UKF)和分块差分滤波(divided differential filter,DDF).尽管目前UKF更为常见,但在设计中UKF需要选择3个采样点权值参数,如果参数选择不当,受数值鲁棒性的限制,实际计算时常常出错.然而目前为止讨论这3个参数如何选择的文献十分罕见. DDF在理论推导中更为复杂,但计算量和UKF同阶,且计算中只需要确定步长一个参数,对于高斯型先验变量,有文献研究表明,最优步长是确定的常量[4].
被动跟踪问题中,受大初始估计误差限制,标准EKF和UKF的估计性能常常难以满足精度要求,目前比较流行的处理方案是采用各种自适应滤波方案,在估计弹目相对运动信息的同时对噪声信息进行估计.文献[14]基于高斯-阿尔米特正定法则给出了一种自适应滤波方法,针对具有线性状态方程和非线性测量方程的典型目标跟踪问题,在测量噪声统计特性未知的情况下取得了较好效果.文献[15]针对传统卡尔曼滤波器在测量噪声统计特性未知时存在的估计精度下降问题,提出了一种能够快速跟踪测量噪声方差的修正贝叶斯自适应卡尔曼估计器(VB-MAKF).文献[16]针对目前流行的容积卡尔曼滤波(cubature Kalman filter,CKF)在运动模型不确定时滤波精确度下降甚至发散的问题,提出一种强跟踪自适应CKF算法,在系统存在模型不确定性及测量信息不良时,保障了良好的鲁棒性和较高的滤波精确度.
然而目前为止,目前各类文献较少涉及被动跟踪问题中同时估计测量噪声和系统噪声的滤波方法.为解决上述问题,文章利用统计线性化(statistical linear regression)思想改进了传统迭代EKF[10].在此基础上结合DDF,发展了一种带有噪声智能统计功能的自适应迭代DDF算法.该算法引入智能虚拟噪声策略对测量噪声和系统噪声进行同时估计,有效补偿了误差传递对滤波精度的影响,对于具有线性系统模型和非线性测量模型的典型仅有角度被动跟踪估计问题,在系统噪声幅度不大的情况下,针对较大的初始状态估计误差,较好完成了系统和测量噪声统计特性未知情况下的非线性估计任务,扩展了传统DDF算法在未知噪声统计环境下的应用范围.
1 分块差分滤波器考虑非线性系统
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{f}}_k}\left( {{\mathit{\boldsymbol{x}}_{k - 1}}, {\mathit{\boldsymbol{u}}_{1\left( {k - 1} \right)}}} \right) + {\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{w}}_k}.\\ {\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{h}}_k}\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right) + {\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{v}}_k}. \end{array} \right. $ | (1) |
其中xk、yk分别为状态向量和测量向量,fk、hk为两个非线性时变函数, u1(k-1)、u2(k)分别为过程方程和测量方程的确定性输入;Gk, Lk分别为过程噪声和测量噪声的加权矩阵,且过程噪声wk和测量噪声vk均服从高斯分布,即有wk~N(qk, Qk),vk~N(rk), Rk;另外,不失一般性, 可认为上述两类噪声和系统的初始状态x0三者彼此互不相关.系统(1)的DDF算法分为4个步骤.
步骤1 初始化.令L为系统状态向量的维数;l为算法步长,有
| $ {{\mathit{\boldsymbol{\hat x}}}_0} = E\left[ {{\mathit{\boldsymbol{x}}_0}} \right], {\mathit{\boldsymbol{P}}_0} = E\left[ {\left( {{\mathit{\boldsymbol{x}}_0} - {{\mathit{\boldsymbol{\hat x}}}_0}} \right){{\left( {{\mathit{\boldsymbol{x}}_0} - {{\mathit{\boldsymbol{\hat x}}}_0}} \right)}^{\rm{T}}}} \right]. $ | (2) |
式中E为数学期望,
步骤2 计算输入向量的协方差矩阵.对于k=1, 2,…, ∞,有
| $ \mathit{\boldsymbol{S}}_{k - 1}^i = l{\left( {\sqrt {{\mathit{\boldsymbol{P}}_{k - 1}}} } \right)_i}, i = 1, 2, \cdots , L. $ | (3) |
式中下角标i为矩阵的第i行,l为步长参数,L为状态方程的维数,
步骤3 时间更新.对于k=1, 2, …, ∞,有
| $ \begin{array}{l} {\mathit{\boldsymbol{a}}^i} = {\mathit{\boldsymbol{f}}_k}\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}} + \mathit{\boldsymbol{S}}_{k - 1}^i, {\mathit{\boldsymbol{u}}_{1\left( {k - 1} \right)}}} \right) - {\mathit{\boldsymbol{f}}_k}\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}} - } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{S}}_{k - 1}^i, {\mathit{\boldsymbol{u}}_{1\left( {k - 1} \right)}}} \right), \end{array} $ | (4) |
| $ \begin{array}{l} {\mathit{\boldsymbol{b}}^i} = {f_k}\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}} + \mathit{\boldsymbol{S}}_{k - 1}^i, {\mathit{\boldsymbol{u}}_{1\left( {k - 1} \right)}}} \right) + {\mathit{\boldsymbol{f}}_k}\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}} + } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{S}}_{k - 1}^i, {\mathit{\boldsymbol{u}}_{1\left( {k - 1} \right)}}} \right) - 2{\mathit{\boldsymbol{f}}_k}\left( {{{\mathit{\boldsymbol{\hat x}}}_{k - 1}}, {\mathit{\boldsymbol{u}}_{1\left( {k - 1} \right)}}} \right), \end{array} $ | (5) |
| $ \begin{array}{l} \mathit{\boldsymbol{P}}_k^ - = \frac{1}{{4{l^2}}}\sum\limits_{i = 1}^L {\left( {{\mathit{\boldsymbol{a}}^i}{{\left( {{\mathit{\boldsymbol{a}}^i}} \right)}^{\rm{T}}}} \right)} + \frac{{{l^2} - 1}}{{4{l^4}}}\sum\limits_{i = 1}^L {\left( {{\mathit{\boldsymbol{b}}^i}{{\left( {{\mathit{\boldsymbol{b}}^i}} \right)}^{\rm{T}}}} \right)} + \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{O}}_k}\mathit{\boldsymbol{G}}_k^{\rm{T}}. \end{array} $ | (6) |
步骤4 测量更新.对于k=1, 2,…, ∞,有
| $ S_k^i = {\left( {l\sqrt {\mathit{\boldsymbol{P}}_k^ - } } \right)_i}, i = 1, 2, \cdots , L, $ | (7) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat y}}_k^ - = \frac{{{l^2} - L}}{{{l^2}}}{\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - , {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right) + {\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{r}}_k} + \\ \;\;\;\;\;\;\;\frac{1}{{2{l^2}}}\sum\limits_{i = 1}^L {\left[ {{\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - + \mathit{\boldsymbol{S}}_k^i, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right) + } \right.} \\ \;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - - \mathit{\boldsymbol{S}}_k^i, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right)} \right], \end{array} $ | (8) |
| $ {\mathit{\boldsymbol{c}}^i} = {\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - + \mathit{\boldsymbol{S}}_k^i, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right) - {\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - - \mathit{\boldsymbol{S}}_k^i, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right), $ | (9) |
| $ \begin{array}{l} {\mathit{\boldsymbol{d}}^i} = {\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - + \mathit{\boldsymbol{S}}_k^i, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right) + {\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - - \mathit{\boldsymbol{S}}_k^i, {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right) - \\ \;\;\;\;\;\;\;2{\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^ - , {\mathit{\boldsymbol{u}}_{2\left( k \right)}}} \right), \end{array} $ | (10) |
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{\tilde y\left( k \right)}} = \frac{1}{{4{l^2}}}\sum\limits_{i = 1}^L {\left( {{\mathit{\boldsymbol{c}}^i}{{\left( {{\mathit{\boldsymbol{c}}^i}} \right)}^{\rm{T}}}} \right)} + {\mathit{\boldsymbol{L}}_k}{\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{L}}_k^{\rm{T}} + \\ \;\;\;\;\;\;\;\;\;\;\frac{1}{{6{l^2}}}\sum\limits_{i = 1}^L {\left( {{\mathit{\boldsymbol{d}}^i}{{\left( {{\mathit{\boldsymbol{d}}^i}} \right)}^{\rm{T}}}} \right)} , \end{array} $ | (11) |
| $ {\mathit{\boldsymbol{P}}_{x\left( k \right)y\left( k \right)}} = \frac{1}{{2{l^2}}}\sum\limits_{i = 1}^L {\mathit{\boldsymbol{S}}_k^i{{\left[ {{{\left( \mathit{\boldsymbol{c}} \right)}^i}} \right]}^{\rm{T}}}, } $ | (12) |
| $ {\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{x\left( k \right)y\left( k \right)}}{\left( {{\mathit{\boldsymbol{P}}_{\tilde y\left( k \right)}}} \right)^{ - 1}}, $ | (13) |
| $ {{\mathit{\boldsymbol{\hat x}}}_k} = \mathit{\boldsymbol{\hat x}}_k^ - + {\mathit{\boldsymbol{K}}_k}\left( {{y_k} - \mathit{\boldsymbol{\hat y}}_k^ - } \right), $ | (14) |
| $ {\mathit{\boldsymbol{P}}_k} = \mathit{\boldsymbol{P}}_k^ - - {\mathit{\boldsymbol{K}}_k}{\mathit{\boldsymbol{P}}_{\tilde y\left( k \right)}}\mathit{\boldsymbol{K}}_k^{\rm{T}}. $ | (15) |
在系统测量模型噪声未知时, 通常可采用迭代方式提高估计精度.然而很多文献的研究表明[1, 9, 12],单纯采用迭代计算的估计精度是有限的.若将非线性函数局部线性化所致截断误差连同真实噪声等效为线性系统模型中的虚拟噪声,则可采用虚拟噪声统计参数和状态联合估计的自适应滤波方法.设虚拟过程噪声和虚拟测量噪声分别为
| $ E\left( {{{\mathit{\boldsymbol{\tilde w}}}_k}} \right) = {{\mathit{\boldsymbol{\tilde q}}}_k}, {\mathop{\rm cov}} \left( {{{\mathit{\boldsymbol{\tilde w}}}_k}} \right) = {{\mathit{\boldsymbol{\tilde Q}}}_k}, $ | (16) |
| $ E\left( {{{\mathit{\boldsymbol{\tilde v}}}_k}} \right) = {{\mathit{\boldsymbol{\tilde r}}}_k}, {\mathop{\rm cov}} \left( {{{\mathit{\boldsymbol{\tilde v}}}_k}} \right) = {{\mathit{\boldsymbol{\tilde R}}}_k}. $ | (17) |
迭代有利于改善线性化的参考点,而虚拟噪声统计估值器则在一定程度上能够估计出线性化后随机误差的“强度”.若在迭代步骤中,既矫正局部线性化参考点,又估计线性化后随机误差的大小,则可以进一步消除线性化误差的影响,这就是自适应迭代扩展卡尔曼滤波(adaptive iterative extended Kalman filter, AIEKF).设
对于i=0, 1, …, N,
| $ \mathit{\boldsymbol{H}}_k^i = {\rm{d}}{\mathit{\boldsymbol{h}}_k}/{\rm{d}}{\mathit{\boldsymbol{x}}_k}\left| {_{{x_k} = \hat x_k^i}} \right., $ | (18) |
| $ \mathit{\boldsymbol{W}}_k^i = \mathit{\boldsymbol{P}}_k^ - {\left( {\mathit{\boldsymbol{H}}_k^i} \right)^{\rm{T}}}{\left[ {\mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{P}}_k^ - {{\left( {\mathit{\boldsymbol{H}}_k^i} \right)}^{\rm{T}}} + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right]^{ - 1}}, $ | (19) |
| $ \mathit{\boldsymbol{\varepsilon }}_k^i = {\mathit{\boldsymbol{y}}_k} - {\mathit{\boldsymbol{h}}_k}\left( {\mathit{\boldsymbol{\hat x}}_k^i} \right), $ | (20) |
| $ \mathit{\boldsymbol{\hat x}}_k^{i + 1} = \mathit{\boldsymbol{\hat x}}_k^ - + \mathit{\boldsymbol{W}}_k^i\left[ {\mathit{\boldsymbol{\varepsilon }}_k^i - H_k^i\left( {\hat x_k^ - - \hat x_k^i} \right)} \right], $ | (21) |
| $ \mathit{\boldsymbol{P}}_k^{i + 1} = \left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{W}}_k^i\mathit{\boldsymbol{H}}_k^i} \right)\mathit{\boldsymbol{P}}_k^ - , $ | (22) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\tilde R}}}_k^{i + 1} = {d_k}\left[ {\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{W}}_k^i} \right)\mathit{\boldsymbol{\varepsilon }}_k^i{{\left( {\mathit{\boldsymbol{\varepsilon }}_k^i} \right)}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{W}}_k^i} \right)}^{\rm{T}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{P}}_k^{i + 1}{{\left( {\mathit{\boldsymbol{H}}_k^i} \right)}^{\rm{T}}}} \right] + \left( {1 - {d_k}} \right)\mathit{\boldsymbol{\hat {\tilde R}}}_k^i, \end{array} $ | (23) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\tilde Q}}}_k^{i + 1} = {d_k}\left[ {\mathit{\boldsymbol{W}}_k^i\mathit{\boldsymbol{\varepsilon }}_k^i{{\left( {\mathit{\boldsymbol{\varepsilon }}_k^i} \right)}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{W}}_k^i} \right)}^{\rm{T}}} + \mathit{\boldsymbol{P}}_k^{i + 1}} \right] + \\ \;\;\;\;\;\;\;\;\;\left( {1 - {d_k}} \right)\mathit{\boldsymbol{\hat {\tilde Q}}}_k^i. \end{array} $ | (24) |
式中dk为0~1之间的某个常数,如果采用UKF计算状态变量的预测值,结合式(18)、(24),即得到了自适应无迹卡尔曼滤波(adaptive iterative unscented Kalman filter, AIUKF)算法.
3 分块差分噪声智能统计滤波器同EKF相比,显然基于统计线性化的理论设计的DDF更为精确.为进一步提高DDF的精度,受AIEKF方法的启发,可以考虑采用迭代和自适应机制智能化DDF.
3.1 线性化误差传递将状态变量的迭代更新表达进一步展开得到
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}_k^{i + 1} = \mathit{\boldsymbol{\hat x}}_k^ - + P_k^ - {{\left( {\mathit{\boldsymbol{H}}_k^i} \right)}^{\rm{T}}}{{\left[ {\mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{P}}_k^ - {{\left( {\mathit{\boldsymbol{H}}_k^i} \right)}^{\rm{T}}} + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right]}^{ - 1}}}\cdot \\ {\left[ {\mathit{\boldsymbol{\varepsilon }}_k^i - \mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{P}}_k^ - {{\left( {\mathit{\boldsymbol{P}}_k^ - } \right)}^{ - 1}}\left( {\mathit{\boldsymbol{\hat x}}_k^ - - \mathit{\boldsymbol{\hat x}}_k^i} \right)} \right], } \end{array} $ | (25) |
注意到在该式中存在线性化误差传递项Pk-(Hki)T和HkiPk-(Hki)T.若定义线性化函数zk=Hkixk则利用数学期望运算的线性性质可得
| $ \begin{array}{l} {\mathop{\rm cov}} \left( {{{\boldsymbol{z}}_k}} \right) = E\left[ {\left( {\mathit{\boldsymbol{H}}_k^i{\mathit{\boldsymbol{x}}_k} - \mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{\hat x}}_k^ - } \right)} \right.\left( {\mathit{\boldsymbol{H}}_k^i{\mathit{\boldsymbol{x}}_k} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left. {\mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{\hat x}}_k^ - } \right)}^{\rm{T}}}} \right] = \mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{P}}_k^ - {\left( {\mathit{\boldsymbol{H}}_k^i} \right)^{\rm{T}}}, \end{array} $ | (26) |
| $ \begin{array}{l} {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right) = E\left[ {\left( {{\mathit{\boldsymbol{x}}_k} - \mathit{\boldsymbol{\hat x}}_k^ -} \right)\left( {\mathit{\boldsymbol{H}}_k^i{\mathit{\boldsymbol{x}}_k} - } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left. {\mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{\hat x}}_k^ - } \right)}^{\rm{T}}}} \right] = \mathit{\boldsymbol{P}}_k^ - {\left( {\mathit{\boldsymbol{H}}_k^i} \right)^{\rm{T}}}, \end{array} $ | (27) |
| $ \text{cov}\left( {{\mathit{\boldsymbol{z}}_k}, {\mathit{\boldsymbol{x}}_k}} \right) = {\mathop{\rm cov}} {\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right)^{\rm{T}}} = \mathit{\boldsymbol{H}}_k^i\mathit{\boldsymbol{P}}_k^ - . $ | (28) |
故AIEKF状态测量更新迭代过程可以改写为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}_k^{i + 1} = \mathit{\boldsymbol{\hat x}}_k^ - + {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right){{\left[ {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right]}^{ - 1}} \cdot \left[ {\mathit{\boldsymbol{\varepsilon }}_k^i - } \right.}\\ {\left. {{\mathop{\rm cov}} {{\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right)}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{P}}_k^ - } \right)}^{ - 1}}\left( {\mathit{\boldsymbol{\hat x}}_k^ - - \mathit{\boldsymbol{\hat x}}_k^i} \right)} \right], } \end{array} $ | (29) |
同理可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{P}}_k^{i + 1} = \mathit{\boldsymbol{P}}_k^ - - {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right)\left[ {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + } \right.}\\ {{{\left. {\mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right]}^{ - 1}} \cdot {\mathop{\rm cov}} {{\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right)}^{\rm{T}}}, } \end{array} $ | (30) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\tilde R}}}_k^{i + 1} = \left( {1 - {d_k}} \right)\mathit{\boldsymbol{\hat {\tilde R}}}_k^i + {d_k}\left\{ {\left[ {\mathit{\boldsymbol{I}} - {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right){{\left( {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}} \right] \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\varepsilon }}_k^i{\left( {\mathit{\boldsymbol{\varepsilon }}_k^i} \right)^{\rm{T}}}{\left[ {\mathit{\boldsymbol{I}} - {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right){{\left( {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\left. {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) - {\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right){{\left( {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right)} \right\}, \end{array} $ | (31) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\tilde Q}}}_k^{i + 1} = {d_k}\left\{ {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right){{\left( {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}} \cdot \mathit{\boldsymbol{\varepsilon }}_k^i{{\left( {\mathit{\boldsymbol{\varepsilon }}_k^i} \right)}^{\rm{T}}} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;{\left[ {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right){{\left( {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}} \right]^{\rm{{\rm T}}}} + \mathit{\boldsymbol{P}}_k^ - - \\ \;\;\;\;\;\;\;\;\;\left. {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right) \cdot {{\left( {{\mathop{\rm cov}} \left( {{\mathit{\boldsymbol{z}}_k}} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}{\mathop{\rm cov}} {{\left( {{\mathit{\boldsymbol{x}}_k}, {\mathit{\boldsymbol{z}}_k}} \right)}^{\rm{T}}}} \right\} + \\ \;\;\;\;\;\;\;\;\;\left( {1 - {d_k}} \right)\mathit{\boldsymbol{\hat {\tilde Q}}}_k^i. \end{array} $ | (32) |
上述方程基于对观测函数的线性化处理,以及对状态和测量变量的线性化误差传递.事实上可以采用更为精确的误差传递方法,比如统计线性化误差传递来改进迭代过程和虚拟噪声估值器.
3.2 统计线性化误差传递通常统计线性化误差传递同基于一阶泰勒序列展开的误差传递相比更为精确.这种方法对任意非线性函数统计量的逼近精度至少达到二阶.利用该思想,测量更新迭代过程中的误差传递项可利用如下Sigma点采样策略方式计算.
令nx、nz分别为系统状态向量和测量向量的维数,有
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\chi }}_0} = \mathit{\boldsymbol{\hat x}}_k^i;\\ {\mathit{\boldsymbol{\chi }}_j} = \mathit{\boldsymbol{\hat x}}_k^i + {\left( {\sqrt {\left( {{n_x} + \gamma } \right)} \mathit{\boldsymbol{P}}_k^i} \right)_j}, \;\;\;\;j = 1, 2, \cdots , {n_x};\\ {\mathit{\boldsymbol{\chi }}_j} = \mathit{\boldsymbol{\hat x}}_k^i - {\left( {\sqrt {\left( {{n_x} + \gamma } \right)} \mathit{\boldsymbol{P}}_k^i} \right)_{j - {n_x}}}, \;\;\;\;j = {n_x} + 1, \cdots , 2{n_x}. \end{array} \right. $ | (33) |
| $ {\mathit{\boldsymbol{\xi }}_j} = \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{\chi }}_j}} \right), $ | (34) |
| $ \mathit{\boldsymbol{\bar \xi = }}\sum\limits_{j = 0}^{2{n_x}} {\mathit{\boldsymbol{w}}_j^{\left( m \right)}{\mathit{\boldsymbol{\xi }}_j}} , $ | (35) |
| $ {\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) = \sum\limits_{j = 0}^{2{n_x}} {\mathit{\boldsymbol{w}}_j^{\left( c \right)}\left( {{\mathit{\boldsymbol{\xi }}_j} - \mathit{\boldsymbol{\bar \xi }}} \right){{\left( {{\mathit{\boldsymbol{\xi }}_j} - \mathit{\boldsymbol{\bar \xi }}} \right)}^{\rm{T}}}} , $ | (36) |
| $ {\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right) = \sum\limits_{j = 0}^{2{n_x}} {\mathit{\boldsymbol{w}}_j^{\left( c \right)}\left( {{\mathit{\boldsymbol{\chi }}_j} - \mathit{\boldsymbol{\hat x}}_k^i} \right){{\left( {{\mathit{\boldsymbol{\xi }}_j} - \mathit{\boldsymbol{\bar \xi }}} \right)}^{\rm{T}}}} . $ | (37) |
其中cov(ξ)、cov(χ, ξ)为统计误差传递项.
3.3 新型自适应迭代滤波器从式(29)~(32)中可以看出,改写AIEKF测量更新迭代方程后,表达式不再依赖测量模型的雅可比矩阵,而是以误差传递项表示.这样就可以利用式(36)~(37)统计误差传递项代替式(29)~(32)的线性误差传递项.从而得到新的测量更新迭代过程方程为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}_k^{i + 1} = \mathit{\boldsymbol{\hat x}}_k^ - + {\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right){{\left[ {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right]}^{ - 1}}\left[ {\mathit{\boldsymbol{\varepsilon }}_k^i - } \right.}\\ {\left. {{\mathop{\rm cov}} {{\left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right)}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{P}}_k^ - } \right)}^{ - 1}}\left( {\mathit{\boldsymbol{\hat x}}_k^ - - \mathit{\boldsymbol{\hat x}}_k^i} \right)} \right], } \end{array} $ | (38) |
| $ \begin{array}{l} \mathit{\boldsymbol{P}}_k^{i + 1} = \mathit{\boldsymbol{P}}_k^ - - {\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right)\left[ {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;{\left. {\mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right]^{ - 1}}{\mathop{\rm cov}} {\left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right)^{\rm{T}}}, \end{array} $ | (39) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\tilde R}}}_k^{i + 1} = {d_k}\left\{ {\left[ {\mathit{\boldsymbol{I}} - {\mathop{\rm cov}} \left( \xi \right){{\left( {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}} \right] \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\varepsilon }}_k^i{\left( {\mathit{\boldsymbol{\varepsilon }}_k^i} \right)^{\rm{T}}}{\left[ {I - {\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right){{\left( {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}} \right]^{\rm{T}}} + \\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) - {\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right){{\left( {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right)} \right\} + \\ \;\;\;\;\;\;\;\;\;\;\left( {1 - {d_k}} \right)\mathit{\boldsymbol{\hat {\tilde R}}}_k^i, \end{array} $ | (40) |
| $ \begin{array}{l} \mathit{\boldsymbol{\hat {\tilde Q}}}_k^{i + 1} = {d_k}\left\{ {{\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right){{\left( {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}\mathit{\boldsymbol{\varepsilon }}_k^i{{\left( {\mathit{\boldsymbol{\varepsilon }}_k^i} \right)}^{\rm{T}}} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;{\left[ {{\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right){{\left( {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}} \right]^{\rm{T}}} + \mathit{\boldsymbol{P}}_k^ - - \\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathop{\rm cov}} \left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right){{\left( {{\mathop{\rm cov}} \left( \mathit{\boldsymbol{\xi }} \right) + \mathit{\boldsymbol{\hat {\tilde R}}}_k^i} \right)}^{ - 1}}{\mathop{\rm cov}} {{\left( {\mathit{\boldsymbol{\chi }}, \mathit{\boldsymbol{\xi }}} \right)}^{\rm{T}}}} \right\} + \\ \;\;\;\;\;\;\;\;\;\;\left( {1 - {d_k}} \right)\mathit{\boldsymbol{\hat {\tilde Q}}}_k^i. \end{array} $ | (41) |
由于引入S-H智能噪声统计估值器,式(38)~(41)在测量更新步骤实现了测量对未知过程和测量噪声的智能统计处理,同时对状态变量的迭代更新过程进一步提高了算法对于复杂非线性函数的适应能力,上述公式结合DDF中的状态预测方程(2)~(8),就得到分块差分噪声智能统计滤波器(intelligent statistical divided differential filter, ISDDF).
4 仿真验证考虑三维空间中仅有角度测量的寻的制导问题.其追踪几何如图 1所示.选取直角坐标系建立寻的系统数学模型,其状态向量记作
| $ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_x}}&{{\mathit{\boldsymbol{r}}_y}}&{{\mathit{\boldsymbol{r}}_z}}&{{\mathit{\boldsymbol{v}}_x}}&{{\mathit{\boldsymbol{v}}_y}}&{{\mathit{\boldsymbol{v}}_z}}&{{\mathit{\boldsymbol{a}}_{tx}}}&{{\mathit{\boldsymbol{a}}_{ty}}}&{{\mathit{\boldsymbol{a}}_{tz}}} \end{array}} \right]^{\rm{T}}}. $ |

|
图 1 导弹-目标拦截几何 Figure 1 Missile-target interception geometry |
其中rx、ry、rz为目标与导弹之间的相对位置在直角坐标系中的3个分量;vx、vy、vz为目标与导弹之间的相对速度在直角坐标系中的3个分量;而atx、aty、atz为目标加速度在直角坐标系中的3个分量.
采用经典Singer模型进行建模[1], 其系统模型可以表示为
| $ {\mathit{\boldsymbol{x}}_k} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}_{k - 1}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{u}}_{k - 1}} + {\mathit{\boldsymbol{w}}_{k - 1}}, $ | (42) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_3}}&{\Delta t{\mathit{\boldsymbol{I}}_3}}&{\frac{1}{{{\lambda ^2}}}\left( {{{\rm{e}}^{ - \lambda \Delta t}} + \lambda \Delta t - 1} \right){\mathit{\boldsymbol{I}}_3}}\\ {{{\bf{0}}_3}}&{{\mathit{\boldsymbol{I}}_3}}&{\frac{1}{\lambda }\left( {1 - {{\rm{e}}^{ - \lambda \Delta t}}} \right){\mathit{\boldsymbol{I}}_3}}\\ {{{\bf{0}}_3}}&{{{\bf{0}}_3}}&{{{\rm{e}}^{ - \lambda \Delta t}}{\mathit{\boldsymbol{I}}_3}} \end{array}} \right], $ | (43) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} = }}{\left[ {\begin{array}{*{20}{c}} { - \left( {\Delta {t^2}/2} \right){\mathit{\boldsymbol{I}}_3}}&{ - \Delta t{\mathit{\boldsymbol{I}}_3}}&{{0_3}} \end{array}} \right]^{\rm{T}}}. $ | (44) |
式中uk为导弹加速度;I3为3×3单位矩阵;Δt为采样周期;λ为目标机动频率;wk为符合高斯分布的过程噪声,其均值为0,其协方差为
| $ {\mathit{\boldsymbol{Q}}_k} = \left[ {\begin{array}{*{20}{c}} {{{\bf{0}}_6}}&{{{\bf{0}}_{6 \times 3}}}\\ {{{\bf{0}}_{3 \times 6}}}&{{\sigma ^2}{\mathit{\boldsymbol{I}}_3}} \end{array}} \right], $ | (45) |
其测量模型可表示为
| $ \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_k}} \right) = \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_k}} \right) + {\mathit{\boldsymbol{v}}_k}. $ | (46) |
式中
| $ \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_k}} \right) = {\left[ {\begin{array}{*{20}{c}} {\arctan \frac{{{r_{y, k}}}}{{\sqrt {r_{x, k}^2 + r_{z, k}^2} }}}&{\arctan \frac{{ - {r_{z, k}}}}{{{r_{x, k}}}}} \end{array}} \right]^{\rm{T}}}, $ | (47) |
vk为零均值高斯白测量噪声,其协方差为
| $ {\mathit{\boldsymbol{R}}_k} = \left[ {{\delta _0} + {\delta _1}/\left( {r_{x, k}^2 + r_{y, k}^2 + r_{z, k}^2} \right)} \right]{\mathit{\boldsymbol{I}}_2}, $ | (48) |
其中δ0、δ1均为常量.
分别采用论文中提出的ISDDF算法、文献[13]提出的高斯-阿尔米特测量噪声自适应非线性统计估值器(AGHF)、文献[14]提出的修正贝叶斯变种自适应噪声统计估值器(MVBAKF)、以及文献[15]中提出的自适应强跟踪容积卡尔曼滤波器(ASCKF)算法对系统状态进行估计,设制导初始时刻弹目间的状态初值x0=[3500 1500 1000 -1 100 -150 -50 10 10 10]T,其中相对距离、相对速度和目标加速度的单位分别为m、m/s和m/s2.此外设λ=1 s-1,σ2=0.1 m2/s4,δ0=10-8 rad2/s2,δ1=10-1 rad2,采样周期为0.01 s.考虑末制导过程中可能存在较大的状态初始估计误差,因此在4种滤波器中,状态估计的初值均统一取作
分别对整个末制导过程中弹目相对距离、相对速度、相对加速度和测量噪声这些制导过程中导引律设计需要用到的重要参数进行估计.在ISDDF和AICKF中,对虚拟测量噪声的协方差采用保守的先验估计:
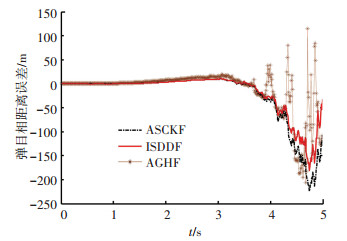
图 2~6分别给出了几种估计算法对于导弹和目标相对位置、相对速度,和目标加速度的仿真曲线. 图 2给出了单次仿真中对于弹目距离的估计曲线,图 3给出了100次蒙特卡洛仿真得出的相对距离RMS误差,从图中可以看出,在几种算法中,ISDDF算法具有较小的估计误差,最大跟踪误差小于100 m,且制导末期弹目相对距离估计发散不明显,而其他几种算法均出现了不同程度的发散问题.
|
图 2 单次仿真中的弹目相对距离估计误差 Figure 2 Estimation error of missile-target relative distance in single simulation |

|
图 3 弹目相对距离估计RMS误差 Figure 3 Missile-target relative distance estimation RMS error |
|
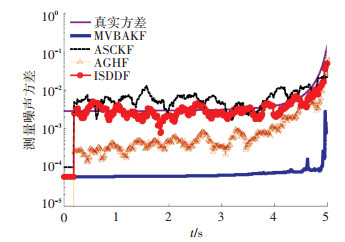
图 4 测量噪声方差估计 Figure 4 Noise measurement variance estimation |
|
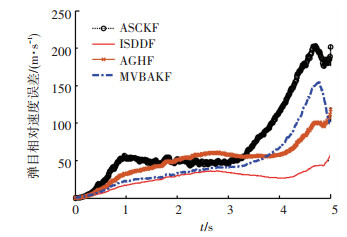
图 5 弹目相对速度估计RMS误差 Figure 5 Missile-target relative speed estimation RMS error |

|
图 6 目标加速度估计RMS误差 Figure 6 Target acceleration estimation RMS error |
图 4采用半对数坐标,给出了几种算法对于测量噪声方差的估计状况,从图中可以看出,ISDDF和ASCKF算法对于测量方差噪声跟踪效果较好,相对而言AGHF算法跟踪速度较慢,跟踪误差较大,而MVBAKF算法则几乎不能跟踪时变的测量方差.
图 5给出的相对速度估计曲线中,可以看出文章给出的ISDDF算法估计精度要显著高于另外3种算法,且制导末端滤波器性能稳定,发散不明显.
图 6给出了几种算法对于目标加速度的估计状况,从图中可以看出,虽然可以保证最终收敛,但AGHF在跟踪初始阶段存在严重的震荡,而ASCKF和ISDDF算法在整个跟踪过程中表现稳定,且估计精度较高.
综上可见在4类算法中,文章给出的ISDDF算法在末制导过程中,对于弹目相对距离、相对速度、目标加速度以及测量噪声方差这几类重要的制导参数的估计精度较高,收敛速度较快,鲁棒性较好,综合估计效果好.
5 结论1) 研究了寻的制导系统中仅有角度测量时的被动跟踪问题,对于具有线性系统模型和非线性测量模型的典型模型,在系统噪声初始估计误差不大的情况下,针对较大的初始状态估计误差,给出了一种估计精度高、鲁棒性好的自适应滤波器的设计方法.
2) 利用统计线性化处理误差传递项的思想,给出了一种带噪声统计功能的分块差分滤波方法.该方法利用采样策略改善非线性分布逼近的同时,通过引入迭代和虚拟噪声机制进一步补偿了估计误,实现了对于测量噪声和系统噪声的同时自适应估计.
| [1] |
周荻. 寻的导弹新型导引规律[M]. 北京: 国防工业出版社, 2002. ZHOU Di. New guidance laws for homing missiles[M]. Beijing: National Defense Industrial Press, 2002. |
| [2] |
汪语哲, 史小平, 朱胤. 抑制闪烁噪声的SMM-IUKF目标跟踪算法[J]. 哈理工大学学报, 2010, 15(5): 69. WANG Yuzhe, SHI Xiaoping, ZHU Yin. A SMM-IUKF tracking method against target glint[J]. Journal of Harbin University of Science and Technology, 2010, 15(5): 69. |
| [3] |
BAR S Y, LI X R, KIRUBARAJAN T. Estimation with application to tracking and navigation: theory, algorithm, and soft-ware[M]. New York: John Wiley & Sons, Inc, 2001.
|
| [4] |
MOHAMED W M, GEORGE K I M, RAYMOND G G. An optimization based approach for relative localization and relative tracking control in multi-robot systems[J]. Journal of Intelligent and Robotic Systems: Theory and Applications, 2016, 85(8): 1. |
| [5] |
BELL B M, CATHEY F W. The iterated Kalman filter as a Gauss-Newton method[J]. IEEE Trans on Automatic Control, 1993, 38(2): 294. DOI:10.1109/9.250476 |
| [6] |
SIMON D. Optimal state estimation: Kalman, Hinf, and nonlinear approaches[M]. New Jersey: John Wiley & Sons, Inc, 2006.
|
| [7] |
ZHOU Di, MU C D, XU W L. Adaptive two step filter with applications to bearings only measurement problem[J]. Journal of Guidance, Control, and Dynamics, 1999, 22(5): 726. DOI:10.2514/2.4443 |
| [8] |
ZHANG Wenjie, WANG Shiyuan, FENG Yali. Novel simplex Kalman filters[J]. Circuits, Systems, and Signal Processing, 2017, 36(2): 879. DOI:10.1007/s00034-016-0323-6 |
| [9] |
王硕.非理想条件下非线性滤波及多传感器信息融合算法研究[D].哈尔滨: 哈尔滨工业大学, 2016 WANG Shuo. Research on nonlinear filtering methods under non-ideal conditions and algorithms for multi-sensors information fusion[D]. Harbin: Harbin Institute of Technology, 2016 |
| [10] |
FU Chunling, ZHANG Jin. Observation bootstrapping CDK-GMPHD filter based on consensus fusion strategy[J]. Optik, 2017, 136(1): 301. |
| [11] |
LI P H, ZHANG T W, MA B. Unscented kalman filter for visual curve tracking[J]. Image and Vision Computing, 2004, 22(2): 157. DOI:10.1016/j.imavis.2003.07.004 |
| [12] |
张永安.非线性滤波及其在寻的制导中的应用[D].哈尔滨: 哈尔滨工业大学, 2003 ZHANG Yongan, Nonlinear filtering with applications to homing guidance[D].Harbin: Harbin Institute of Technology, 2003 |
| [13] |
王睿, 杨晓峰, 彭力. 带二次约束的容积卡尔曼目标跟踪算法[J]. 计算机工程与应用, 2017, 53(1): 142. WANG Rui, YANG Xiaofeng, PENG Li. Target tracking algorithm based on cubature Kalman filter with quadratic equality constraints[J]. Computer Engineering and Applications, 2017, 53(1): 142. DOI:10.3778/j.issn.1002-8331.1503-0371 |
| [14] |
ARITRO D, SMITA S, TAPAN K G. Adaptive Gauss-Hermite filter for non-linear systems with unknown measurement noise covariance[J]. IET Science, Measurement & Technology, 2015, 9(8): 1007. |
| [15] |
WANG Shiyuan, YIN Chao, DUAN Shukai, et al. A modified variational Bayesian noise adaptive Kalman filter[J]. Circuits, Systems, and Signal Processing, 2017, 36(10): 4260. DOI:10.1007/s00034-017-0497-6 |
| [16] |
徐树生, 李娟, 温利, 等. 强跟踪自适应CKF及其在动力定位中应用[J]. 电机与控制学报, 2015, 19(2): 101. XU Shusheng, LI Juan, WEN Li, et al. Strong tracking adaptive CKF and application for dynamic positioning[J]. Electric Machines and Control, 2015, 19(2): 101. |
 2018, Vol. 50
2018, Vol. 50


