2. 北京航天控制仪器研究所,北京 100039
2. Beijing Institute of Aerospace Control Instrument, Beijing 100039, China
原子干涉磁力仪是基于激光光场与原子相互作用时发生量子干涉现象的一种新型磁力仪.与其他常用的磁力仪相比,其具有动态范围宽和灵敏度高的特点,灵敏度理论上可达0.000 5 nT/
原子干涉磁力仪由于以上这些优势近年来广受关注,已有不少研究者开展相关研究.文献[1]基于激光束与处于微弱磁场中的铷原子相互作用,通过测量透过铷原子气体的激光强度的变化来获得磁场信息,结合调制和同步检测技术来消除噪声、增强信号并优化参数.文献[2]从理论上分析了自旋投影噪声、光子散粒噪声和光频移对Cs原子SERF磁力计灵敏度的影响,为提高磁力仪灵敏提供了一定的物理基础.文献[3]对铯原子光泵磁力仪进行优化,在保障较高精度的前提下,将光路部分集成为尺寸较小的光学探头,控制部分用独立的电路模块代替商用模块,实现磁场的闭环锁定,从而实现磁力仪的小型化和低功耗设计.文献[4]针对交变弱磁场的检测,研制了一种基于极化检测双光束结构的激光抽运铷原子磁力仪,通过对极化磁场进行选择,使磁力仪具有更强的灵敏度,从而更好适用于弱磁场磁共振、高频异常物理现象等信号的检测.
目前对于原子干涉磁力仪的研究热点主要集中在提高测量稳定性和灵敏度等方面.通常,在不改变仪器采样率的情况下,磁场测量参考信号的对比度是影响数据处理效果的关键因素,决定了系统的灵敏度和稳定性[5-6].本文通过对传感器探测系统进行数学建模和分析,从信号对比度的角度研究影响信号特性的关键因素,并通过实验来测量实际的对比度数值,分析使系统达到最佳性能状态的参数设置点.
1 物理系统工作原理基于相干布居俘获原理(coherent population trapping, CPT)的原子干涉磁力仪采用碱金属原子作为工作介质,原子的磁子能级在不存在外磁场时是简并的,当加上外磁场后原子能级就会发生塞曼分裂.使用双频相干光与原子作用,当激光频率差与原子基态超精细子能级的劈裂间距精确匹配时,由于激光各个模式从不同跃迁通道激发原子跃迁时产生相互干涉,原子被束缚在不吸收光子的一个暗态上[6-8].这个现象在激光强度变化上表现为原子光谱中出现一条非常窄的暗共振,该谱线在原子干涉磁力仪中作为鉴频信号来反应磁场信息.当采用87Rb作为工作介质时,其原子的能级结构示意图如图 1所示.

|
图 1 原子能级示意图 Figure 1 Schematic diagram of atomic energy level |
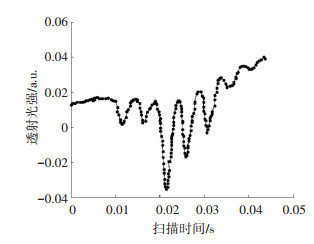
当原子气室被加热到一定温度后,在激光器工作直流电流上注入一定功率的微波,当微波频率与原子基态能级频率差Δhfs的1/2相等时,施加一个10 kHz的扫描锯齿波扫描激光频率便可观察到87Rb原子对双色激光场的吸收谱,如图 2所示.其中峰值最大的吸收峰是由±1级边带叠加在一起形成的;紧邻最大峰的两个峰是由基频和±2级边带产生的,其±2边带的功率较弱,且基频不会对激光进行吸收,在多普勒展宽作用下,形成紧邻的两个较弱峰;次相邻的峰则是由+1、+3级以及-1、-3级边带产生的[9-11],其中,±3边带的功率比±2边带功率更弱,在多普勒展宽的边带交叉作用下形成次相邻的弱峰,依次类推.由于微波调制深度的不同,导致各个边带所占功率的大小不同,各峰幅值的相对比例也有所不同.
|
图 2 碱金属原子对双色光的吸收谱线 Figure 2 Double color light absorption spectrum of alkai metalatoms |
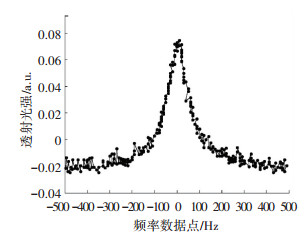
磁力仪使用饱和吸收谱线来稳定激光器的输出光频率,通过逐渐减小激光扫描范围和微调激光器控制电流大小,最终确定吸收谱线最大峰峰值点所对应的激光器工作电流值,以进行激光稳频.当激光频率稳定后,再通过微波频率扫描得到与微波频率相对应的光强信号数据作为鉴频信号.鉴频信号中的一个透射峰如图 3所示.
|
图 3 实验采集的CPT透射峰信号 Figure 3 Transmission peak signal of CPT from experiments |
鉴频信号通常包含CPT主峰及其两侧对称位置出现的若干侧峰,侧峰与主峰峰值点对应的频率差值反映外界的磁场强度信息.因为信号峰值的鉴频准确度会直接影响磁力仪的测量精度,所以如果CPT透射峰信号的对比度增大,鉴频效果会更加理想,有利于提升磁场测量精度.以下将建立数学模型分析传感系统变量与鉴频信号对比度的关系.
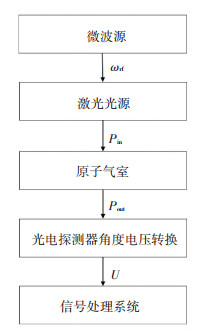
2 物理系统的数学模型原子干涉磁力仪使用光量子传感器来产生鉴频信号,传感器由光源、物理系统、光电探测器和相应的控制电路组成.其中物理系统的主体是碱金属原子气室,外置的微波源为激光器提供高频调制信号,并用该调制激光来激发原子能级跃迁,从而观察原子透射信号.当微波源在中心频率3.417 GHz附近的微小频率区间内进行频率扫描时,光电探测器可以感应连续频率变化下对应的光强变化.传感器的信号传递方式如图 4所示.
|
图 4 CPT磁力仪传感器的信号传递 Figure 4 Signal transmission of CPT magnetometer sensor |
设定微波源输出频率取值的变化和处理器对电压值的采集保持同步,可以获得光功率和对应频率的数据组.控制系统对该数据进行处理,确定鉴频谱线中的透射峰峰值和与之对应的频率值,从而计推算出磁场强度B.在整个传感过程中光电探测器感应到的激光光强信号Pout受到3个主要因素的影响,分别为激光器射入原子气室的入射激光功率Pin、原子气室吸收光功率Pa和鉴频信号的绝对功率Pcpt, Pout可以近似表示为
| $ {P_{{\rm{out}}}} = {P_{{\rm{in}}}} - {P_{\rm{a}}} + {P_{{\rm{cpt}}}}, $ |
原子气室入射激光功率的表达式为
| $ {P_{{\rm{in}}}} = {P_0} + {\varepsilon _{\rm{i}}} \cdot \left( {I - {I_{\rm{C}}}} \right) + {\varepsilon _{\rm{t}}} \cdot \left( {{T_{{\rm{cell}}}} - {T_{\rm{L}}}} \right). $ |
式中:P0为激光器功率初始值;εi为半导体激光器的波长电流因子,εi=0.4×10-6m/A;I为半导体激光器电流;IC为激光器阈值电流;εt为半导体激光器的波长温度因子,εt=0.55×10-9m/K;Tcell为原子气室温度;TL为激光器阈值温度.
原子吸收光功率Pa的数据谱线呈现多普勒线型,当使用线型函数来近似表示原子吸收光强信号谱线的主峰时,可建立的数学表达式为
| $ {P_{\rm{a}}} = \frac{{{P_{{\rm{in}}}} \cdot {{\rm{e}}^{ - \alpha L}} \cdot {D^2}}}{{4{{\left( {{\omega _{\rm{L}}} - {\omega _{\rm{A}}}} \right)}^2} + {D^2}}}. $ |
式中:Pin为原子气室的入射激光强度;ωL为激光器实际输出频率;ωA为激光器实际输出频率和原子跃迁共振频率,ωA=377.1×1012Hz;α为原子气室的吸收系数,D为信号峰的宽度因数,可分别表示为
| $ \alpha = \frac{{{\mathit{\Gamma }^ * } \cdot {\lambda _{\rm{A}}}^3 \cdot N}}{{8{\rm{ \mathit{ π} }}}}\sqrt {\frac{M}{{2{\rm{ \mathit{ π} }} \cdot {K_{\rm{b}}} \cdot {T_{{\rm{cell}}}}}}} , $ |
| $ D = \frac{{2{\omega _{\rm{A}}}}}{C}\sqrt {\frac{{2{K_{\rm{b}}} \cdot {T_{{\rm{cell}}}}}}{M}\ln 2} , $ |
其中λA为原子跃迁波长,N为与光相互作用的原子数密度,M为原子质量,Kb为波尔兹曼常数,Kb=1.38×10-23 J/K,C为光速,Tcell为原子气室温度,Γ为原子激发态能级弛豫率,Pbuffer为气室内缓冲气体压强,Γ*=Γ+150 000·Pbuffer.
CPT共振信号绝对光强度的数学表达为
| $ {P_{{\rm{cpt}}}} = \frac{{H \cdot {{\left( {\Delta \mathit{\boldsymbol{\upsilon }}} \right)}^2}}}{{4{{\left( {{\omega _{{\rm{rf}}}} - \gamma B} \right)}^2} + {{\left( {\Delta \mathit{\boldsymbol{\upsilon }}} \right)}^2}}}. $ |
式中γ为原子旋磁比1阶系数,γ=6.997×109 Hz;ωrf为微波信号频率,ωrf=7×104~7×105 Hz;H为CPT信号幅度,
| $ H = \frac{{\beta \cdot N \cdot S \cdot L \cdot {\mathit{\Omega }^4} \cdot {P_{{\rm{in}}}}}}{{{\mathit{\Gamma }^ * }\left( {\Delta \mathit{\boldsymbol{\upsilon }}} \right)}}\left( {\frac{1}{{{{\left( {{\mathit{\Gamma }^ * }} \right)}^2} + {{\left( {{\omega _{\rm{L}}} - {\omega _{\rm{A}}}} \right)}^2}}}} \right). $ |
其中S为与原子作用的光束横截面积;L为原子气室长度;
从以上模型可以看出,对于原子干涉磁力仪来说,物理系统的输出信号幅度信息对提取频率信息的准确度影响很大,这就要求尽量提高CPT透射信号的对比度.另一方面,信号分析的准确度也受到信号稳定度的影响.原子干涉磁力仪的信号稳定度的表达式[12]为
| $ \sigma \left( \tau \right) \approx \frac{1}{{{R_{{\rm{S}}/{\rm{N}}}}}} \cdot \frac{\Delta {\mathit{\boldsymbol{\upsilon }}}}{{\sqrt N }} \cdot \frac{1}{{\sqrt {\mathit{\boldsymbol{\tau }} }}}. $ |
其中RS/N为谱线信噪比,τ为测量时间,σ(τ)越小表明信号稳定度越好.可以看出,提高CPT信号的信噪比可以有效提高原子磁力仪的信号频率稳定度,而CPT信号的信噪比又与该信号的对比度直接相关.综合以上两方面的因素,信号对比度对于磁力仪系统来说是非常重要的一项指标.根据探测系统的数学模型,使用两部分信号幅度特征的比值来表示CPT信号的对比度,即
| $ \begin{array}{l} {R_{\rm{c}}} = \frac{H}{{{P_{\rm{a}}}}} = \frac{{\beta \cdot N \cdot S \cdot L \cdot {\mathit{\Omega }^4} \cdot {P_{{\rm{in}}}}}}{{{\mathit{\Gamma }^ * }\left( {\Delta \mathit{\boldsymbol{\upsilon }}} \right)}} \cdot \\ \;\;\;\;\;\left( {\frac{1}{{{{\left( {{\mathit{\Gamma }^ * }} \right)}^2} + {{\left( {{\omega _{\rm{L}}} - {\omega _{\rm{A}}}} \right)}^2}}}} \right)/\\ \;\;\;\;\;\left( {\frac{{{P_{{\rm{in}}}} \cdot {{\rm{e}}^{ - \alpha L}} \cdot {D^2}}}{{4{{\left( {{\omega _{\rm{L}}} - {\omega _{\rm{A}}}} \right)}^2} + {D^2}}}} \right). \end{array} $ | (1) |
将式(1)在预设的系统工作点附近作泰勒展开,并略去极小项,可以近似得到系统控制量对信号对比度的影响关系为
| $ \begin{array}{*{20}{c}} {\Delta {R_{\rm{c}}} = {R_{\rm{c}}} - {R_{{\rm{c0}}}} = {K_{{\rm{I\_1}}}} \times \Delta I + {K_{{\rm{I\_2}}}} \times \Delta {I^2} + }\\ {{K_{{T_{{\rm{cell\_1}}}}}} \times \Delta {T_{{\rm{cell}}}} + {K_{{T_{{\rm{cell\_2}}}}}} \times \Delta {T_{{\rm{cell}}}}^2.} \end{array} $ | (2) |
对式(2)使用传感系统的预设工作点来进行求解:I0为激光器电流预设值,I0=1.2 mA;Tcell0为原子气室温度预设值,Tcell0=61.85 ℃;B0为输入磁场强度预设值,B0=10-5T;TL0为激光器温度预设值,TL0=56.85 ℃.式(2)说明激光器电流和原子气室温度是影响信号对比度的关键变量.其中Rc0为系统参数为预设值时的信号对比度,理想的信号对比度量级为6%.为了进一步分析I和Tcell的影响程度,分别求出二者的一阶和二阶系数为
| $ {K_{{\rm{I\_1}}}} = \frac{{\partial {R_{\rm{c}}}}}{{\partial I}} = 1.29 \times {10^{ - 4}}/{\rm{A}}, $ |
| $ {K_{{\rm{I\_2}}}} = \frac{{{\partial ^2}{R_{\rm{c}}}}}{{\partial {I^2}}} = 2 \times {10^{ - 7}}/{{\rm{A}}^2}, $ |
| $ {{K}_{{{\text{T}}_{\text{cell}\_\text{1}}}}}=\frac{\partial {{R}_{\text{c}}}}{\partial {{T}_{\text{cell}}}}=2.09\times {{10}^{3}}{{/}^{{}^\circ }}\text{C}, $ |
| $ {{K}_{{{\text{T}}_{\text{cell}\_\text{2}}}}}=\frac{{{\partial }^{2}}{{R}_{\text{c}}}}{\partial {{T}_{\text{cell}}}^{2}}=-1.55\times {{10}^{-8}}/{{\left( ^{{}^\circ }\text{C} \right)}^{2}}. $ |
由以上结果可知,两个关键变量的一阶系数影响较大.电流I的影响程度在0.13/mA左右, 而温度Tcell的影响程度为0.002/℃.
4 实验CPT信号对比度模型说明了原子干涉磁力仪物理传感器系统内的激光器电流和原子气室温度的影响程度较大,以下分别针对这两个关键变量进行实验,通过对实际数据的分析来验证数学模型的正确性,确定系统参数的优化值.
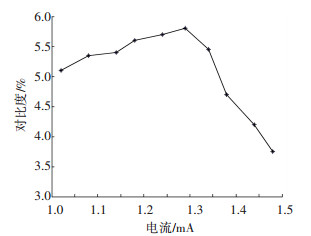
4.1 激光器电流对信号对比度的影响系统使用垂直共振腔表面发射激光(vertical cavity surface emitting laser, VCSEL)作为光源,实验选取在其稳定工作电流附近即1~1.5 mA的范围微调一组电流值来观察鉴频信号的对比度.当物理系统的其他变量稳定之后,记录相应输出信号的对比度数值,得到的实验结果如图 5所示.
|
图 5 CPT信号对比度与激光器光强的数据描点图 Figure 5 Data tracing chart between CPT signal contrast and laser intensity |
可以看到出,在光强较小的情况下,信号对比度随着光强的增大而增大,这是由于光强增大,更多的原子被制备到CPT态,CPT共振信号增强,因此对比度提高.当光强大到一定的程度后,激光对原子的光抽运效果逐渐变得明显,一部分原子被抽运到原子基态磁量子数最大的超精细磁能级形成极化暗态,对CPT态的制备没有贡献,从而导致原子利用率降低,信号对比度降低[13-15].从实验结果来看,CPT信号对比度随电流的变化量级在0.1 mA左右,与模型计算结果相符合.
4.2 原子气室温度对信号对比度的影响在原子气室温度与信号对比度关系的实验中,设置激光器的稳频电流为1.23 mA,温度从70 ℃递减到48 ℃,该温度范围是系统在实际工作中通常会调节的温度区间.信号测量结果如表 3所示,其中VP-P表示CPT信号的峰峰值,Vmax表示CPT信号的最大值.
| 表 3 不同原子气室温度下的CPT信号对比度测量值 Table 3 Measured values of CPT signal contrast at different atomic gas chamber temperature |
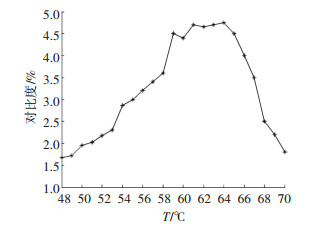
实验数据的拟合曲线如图 6所示.从以上实验结果可以看出,信号对比度的变化量级为0.001/℃左右,与计算结果相符,并且随着原子气室温度的逐渐升高,CPT信号的对比度先升高后降低,由此说明在气室温度与CPT信号幅值关系上存在一个温度优化值.
|
图 6 CPT信号对比度与原子气室温度的数据描点图 Figure 6 Data tracing chart between CPT signal contrast and atomic gas chamber temperature |
1) 从实验结果可以看出,CPT信号对比度在2%~6%左右,考虑到信号处理电路和温控系统对实际信号的影响,该结果与模型计算的6%量级基本相符.传感系统的关键影响因素激光器电流和原子气室温度对CPT信号对比度的影响程度也符合数学模型的计算结果.
2) 从激光器电流和原子气室温度的影响实验中可以看出,在传感系统工作过程中,这两个关键变量存在优化工作范围,可以获得较高的信号对比度.对激光器电流来说,1.28 mA的工作电流所获得对比度约为5.8%,综合测试结果最优,而对于原子气室温度来说,当温度区间在60~65 ℃时CPT信号的对比度值可以达到4.5%以上.
3) 在实际应用中,由于原子干涉磁力仪的传感器系统所使用的原子气室和半导体激光器的性能存在较大的不确定性,通常需要为搭建好的传感系统确定关键变量的优化工作点.通过以上的实验方法将传感器系统的激光器电流和原子气室温度的工作点设置在最优值或者最优工作区间内能够有效提高鉴频信号的对比度,从而提高传感系统的灵敏度和稳定性.
| [1] |
李曙光, 周翔, 曹晓超, 等. 全光学高灵敏度铷原子磁力仪的研究[J]. 物理学报, 2010, 59(2): 877. LI Shuguang, ZHOU Xiang, CAO Xiaochao, et al. All-optical high sensitive atomic magnetometer[J]. Acta Physica Sinica, 2010, 59(2): 877. DOI:10.7498/aps.59.877 |
| [2] |
王丰.激光对铯原子磁力仪灵敏度影响[D].哈尔滨: 哈尔滨工程大学, 2011 WANG Feng.Influence of laser on the sensitivity of cesium atomic magnetometer[D].Harbin: Harbin Engineering University, 2011 |
| [3] |
张斌.小型化铯光泵原子磁力仪研究[D].杭州: 浙江大学, 2015 ZHANG Bin. Research on miniaturized cesium optically pumped atomic magnetometer[D]. Hangzhou: Zhejiang University, 2015 |
| [4] |
汪之国, 罗晖, 樊振方, 等. 极化检测型铷原子磁力仪的研究[J]. 物理学报, 2016, 65(21): 97. WANG Zhiguo, LUO Hui, FAN Zhenfang, et al. Research on an pump-probe rubidium magnetometer[J]. Acta Physica Sinica, 2016, 65(21): 97. DOI:10.7498/aps.65.210702 |
| [5] |
SCHWINDT P D D, KNAPPE S, SHAH V, et al. Chip-scale atomic magnetometer[J]. Applied Physics Letter, 2004, 85(26): 6409. DOI:10.1063/1.1839274 |
| [6] |
KNAPPE S, SHAH V, SCHWINDT P D D, et al. A microfabricated atomic clock[J]. Applied Physics Letters, 2004, 85(9): 1460. DOI:10.1063/1.1787942 |
| [7] |
MESCHER M J, LUTWAK R, VARGHESE M. An ultra-low-power physics package for a chip-scale atomic clock[C]//The International Conference on Solid-State Sensors, Actuators and Microsystems. Seoul: IEEE, 2005: 311. DOI: 10.1109/SENSOR.2005.1496419
|
| [8] |
ROMISCH S, LUTWAK R. Low-power, 4.6-GHz, stable oscillator for CSAC[C]//International Frequency Control Symposium and Exposition. Miami: IEEE, 2006: 448. DOI: 10.1109/FREQ.2006.275427
|
| [9] |
SAFFMAN M, OBLAK D, APPEL J, et al. Spin squeezing of atomic ensembles by multi-colour quantum non-demolition measurements[J]. Physical Review A, 2009, 79(2): 101. DOI:10.1103/PhysRevA.79.023831 |
| [10] |
LUTWAK R, VLITAS P, VARGHESE M, et al. The MAC—a miniature atomic clock[C]//Proceedings of the 2005 IEEE International Frequency Control Symposium and Exposition. Vancouver: IEEE, 2005: 752. DOI: 10.1109/FREQ.2005.1574029
|
| [11] |
ZHANG Jian, Ning Yongqiang, ZENG Yuguang, et al. Design and analysis of high-temperature operating 795 nm VCSELs for chip-scale atomic clocks[J]. Laser Physics Letters, 2013, 10(4): 45802. DOI:10.1088/1612-2011/10/4/045802 |
| [12] |
AL-SAMANEH A, SANAYEH M B, RENZ S, et al. Polarization control and dynamic properties of VCSELs for MEMS atomic clock applications[J]. IEEE Photonics Technology Letters, 2011, 23(15): 1049. DOI:10.1109/LPT.2011.2151853 |
| [13] |
翟造成, 杨佩红. 第三代卫星导航定位系统星载原子钟的新发展[J]. 天文学进展, 2008, 26(4): 301. ZHAI Zaocheng, YANG Peihong. The new creations and development of on-board atomic clocks for the 3rd generation of GNSS[J]. Progress in Astronomy, 2008, 26(4): 301. DOI:10.3969/j.issn.1000-8349.2008.04.001 |
| [14] |
王义遒. 量子频标原理[M]. 北京: 科学出版社, 1986: 241. WANG Yiqiu. Principle of quantum frequency[M]. Beijing: Science Press, 1986: 241. |
| [15] |
DENATALE J F, BORWICK R L, TSAI C, et al. Compact, low-power chip-scale atomic clock[C]//2008 IEEE/ION Position, Location and Navigation Symposium. Monterey: IEEE, 2008: 67. DOI: 10.1109/PLANS.2008.4570007
|
 2018, Vol. 50
2018, Vol. 50


