由于无能耗的推进方式,太阳帆航天器在深空飞行中倍受青睐[1-3].太阳帆通过巨大的帆面反射太阳光,从而获得光压力作为轨道动力.调整帆面姿态可改变其所受光压力的幅值与方向,进而改变轨道推进力.太阳帆姿控执行机构巧妙地借助太阳光压力提供姿态控制力矩,实现了无能耗姿态控制.由于结构简单、可行性强,滑动质量块形式的执行机构受到了广泛关注[4-7].然而此方法只能产生俯仰轴和偏航轴控制力矩,需要配合滚转轴执行机构滚使用.目前所采用的滚转轴执行方案有控制小帆和转轴稳定条等,但它们对太阳帆的展开过程影响较大.文献[5]采用小块帆板的转动产生滚转轴控制力矩,其分离式的安装对帆面展开影响小,是一种新型高效的执行机构.
然而,质量块滑动会改变太阳帆质心位置,在提供控制力矩的同时也致使转动惯量发生变化,这就要求太阳帆姿态控制器具有较强的鲁棒性.此外,光压力矩对太阳帆也有着不可忽视的影响,相同质心/压心偏差的情况下,其所受光压力矩幅值是传统航天器的近100倍;在诸如三体问题等复杂飞行环境下,天体对太阳帆的引力产生的梯度力矩对其姿态也构成了显著干扰,且随轨道位置变化.此类外部干扰力矩要求姿态控制器具有较好的自适应抗扰能力.
许多学者在太阳帆姿态控制设计方面进行了大量研究.文献[6]针对以滑块为执行机构的太阳帆计了2自由度的姿态控制律,不记转动惯量变化设计了前馈+反馈的控制策略.文献[7]同样以滑动质量块作为执行机构,忽略其对转动惯量的影响,分别采用LQR和PID算法为太阳帆设计了双闭环姿态控制器.文献[8-9]都采用顶端小帆方式产生姿态控制力矩,且在控制器设计时皆采用PD控制律,通过选取姿态和转速的反馈增益矩阵实现姿态控制.虽然PID等线性反馈控制方法具有结构简单且应用成熟等特点,但是针对上述帆板-滑块结构的太阳帆,在采用此类方法进行姿控设计时,较难快速选取合适参数,且控制器往往不能获得较强的鲁棒性和自适应能力.
本文采用帆板-滑块结构作为太阳帆姿控执行器,针对该结构工作过程中引起的惯量变化问题,同时考虑航天器所受外部干扰,采用非线性设计方法研究具有强鲁棒性和自适应能力的姿态控制律.然后,考虑执行机构力学特性,解算帆板转角和滑块位置,以实现所提控制策略.
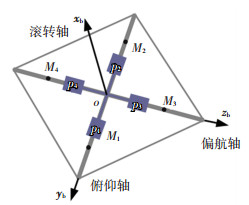
1 问题描述 1.1 姿态动力学与运动学本文以方形太阳帆作为研究对象,为描述其姿态,取太阳帆几何中心o为原点建立本体坐标系,如图 1所示. xb轴沿帆面法线n方向,yb轴沿帆面某一对角线方向,zb轴方向符合右手准则.选用3-2-1转序,采用四元数Q描述太阳帆姿态,则系统运动学与动力学方程分别为
| $ \mathit{\boldsymbol{\dot Q}} = \frac{1}{2}\left[ \begin{array}{l} {q_4}{\mathit{\boldsymbol{I}}_3} + {\mathit{\boldsymbol{q}}^ \times }\\ - {\mathit{\boldsymbol{q}}^{\rm{T}}} \end{array} \right]\mathit{\boldsymbol{\omega }}, $ | (1) |
| $ \mathit{\boldsymbol{J\dot \omega }} + \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }} = {\mathit{\boldsymbol{\tau }}_{\rm{c}}} + {\mathit{\boldsymbol{\tau }}_{\rm{d}}}. $ | (2) |
式中:
干扰力矩主要包括光压干扰力矩τs和引力梯度力矩τg,其中τs=ε0×Fs,ε0为生产工艺导致的质心/压心偏差,Fs为帆面所受太阳光压力.采用理想光学模型,有
| $ {\mathit{\boldsymbol{F}}_{\rm{s}}} = {\left[ {\begin{array}{*{20}{c}} {2{P_{\rm{s}}}A{{\cos }^2}\alpha }&0&0 \end{array}} \right]^{\rm{T}}}. $ |
式中:Ps为一个天文单位处的光压辐射常数,A为太阳帆帆面面积,α为帆面法向量与阳光矢量的夹角,也为太阳帆俯仰角,可通过姿态四元数转换而得.此外,引力梯度力矩由附近天体对太阳帆的引力产生,由于姿态机动时间远小于轨道飞行时间,引力梯度力矩在每个轨道位置可视为常值.
1.2 执行机构动力学帆板-滑块形式的执行机构是文献[5]提出的一类分离式安装的执行机构.长方形帆板pi和质量块Mi(i=1, 2, 3, 4)的安装,如图 1所示,4个帆板/质量块规格一致.工作时,帆板沿对应连接杆转动,连接杆长为l,转角为γi(i=1, 2, 3, 4);质量块沿帆面对角线滑动,记其相对o点的位移为di(i=1, 2, 3, 4).
|
图 1 太阳帆结构 Figure 1 Structure of solar sail |
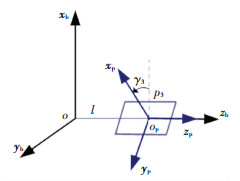
不妨以帆板p3为例,分析移动帆板的工作原理.以帆板质心op为原点建立帆板坐标系oxpypzp,yp轴和zp轴分别平行于帆板两边,xp轴沿帆板法线方向.工作时,p3沿zp轴转动γ3角度,如图 2所示. oxpypzp系与oxbybzb系的变换关系为
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{\rm{b}}}}\\ {{\mathit{\boldsymbol{y}}_{\rm{b}}}}\\ {{\mathit{\boldsymbol{z}}_{\rm{b}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {\gamma _3}}&{\sin {\gamma _3}}&0\\ { - \sin {\gamma _3}}&{\cos {\gamma _3}}&0\\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_{\rm{p}}}}\\ {{\mathit{\boldsymbol{y}}_{\rm{p}}}}\\ {{\mathit{\boldsymbol{z}}_{\rm{p}}}} \end{array}} \right]. $ |
|
图 2 帆板结构 Figure 2 Structure of rotating panel |
在oxpypzp系中,p3反射太阳光获得的光压力为
| $ {\mathit{\boldsymbol{F}}_{{\rm{p3}}}} = 2{P_{\rm{s}}}{A_{\rm{p}}}{\cos ^2}\left( {\alpha + {\gamma _3}} \right){\mathit{\boldsymbol{x}}_{\rm{p}}}, $ |
式中Ap为帆板面积,变换至坐标系oxoyozo中有
| $ {\mathit{\boldsymbol{F}}_{{\rm{p3}}}} = \left[ {\begin{array}{*{20}{c}} {2{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _3}} \right)\cos {\gamma _3}}\\ { - 2{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _3}} \right)\sin {\gamma _3}}\\ 0 \end{array}} \right]. $ |
设op点到o点的距离为l3=lzb,Fp3产生的力矩为
| $ {\mathit{\boldsymbol{\tau }}_{{\rm{p3}}}} = {\mathit{\boldsymbol{l}}_3} \times {\mathit{\boldsymbol{F}}_{{\rm{p3}}}} = \left[ {\begin{array}{*{20}{c}} { - 2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _3}} \right)\sin {\gamma _3}}\\ {2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _3}} \right)\cos {\gamma _3}}\\ 0 \end{array}} \right]. $ |
同理,帆板1、2、4产生的力矩分别为
| $ {\mathit{\boldsymbol{\tau }}_{{\rm{p1}}}} = \left[ {\begin{array}{*{20}{c}} { - 2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _1}} \right)\sin {\gamma _1}}\\ 0\\ { - 2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _1}} \right)\cos {\gamma _1}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{\tau }}_{{\rm{p2}}}} = \left[ {\begin{array}{*{20}{c}} { - 2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _2}} \right)\sin {\gamma _2}}\\ 0\\ {2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _2}} \right)\cos {\gamma _2}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{\tau }}_{{\rm{p4}}}} = \left[ {\begin{array}{*{20}{c}} { - 2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _4}} \right)\sin {\gamma _4}}\\ { - 2l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + {\gamma _4}} \right)\cos {\gamma _4}}\\ 0 \end{array}} \right]. $ |
令γ1=γ2,τp1+τp2=-4lPsApcos2(α+γ1)sinγ1xb;令γ3=γ4,τp3+τp4=-4lPsApcos2(α+γ3)sinγ3xb.可见4块帆板力矩之和只产生滚转轴力矩.俯仰轴和偏航轴控制力矩由滑块滑动提供,结合文献[5]可得执行机构输出的控制力矩为
| $ {\mathit{\boldsymbol{\tau }}_{\rm{c}}} = \left[ {\begin{array}{*{20}{c}} { - 4l{P_{\rm{s}}}{A_{\rm{p}}}\sum\limits_{i = 1, 3} {{{\cos }^2}\left( {\alpha + {\gamma _i}} \right)\sin {\gamma _i}} }\\ { - 2m/{m_{\rm{t}}}\left( {{d_3} + {d_4}} \right){P_{\rm{s}}}A{{\cos }^2}\alpha }\\ {2m/{m_{\rm{t}}}\left( {{d_1} + {d_2}} \right){P_{\rm{s}}}A{{\cos }^2}\alpha } \end{array}} \right]. $ | (3) |
式中m为滑块质量,mt为航天器总质量.
执行机构工作时,由于质量块滑动会引起质心变化,转动惯量J也随之变化.设J=diag(Jxb,Jyb,Jzb),则有
| $ \left\{ \begin{array}{l} {J_{x{\rm{b}}}} = {I_{x{\rm{b}}}} + 2{m_r}d_3^2, \\ {J_{y{\rm{b}}}} = {I_{y{\rm{b}}}} + 2{m_r}d_1^2, \\ {J_{z{\rm{b}}}} = {I_{z{\rm{b}}}} + 2{m_r}\left( {d_1^2 + d_3^2} \right). \end{array} \right. $ | (4) |
式中:mr=m(ms+m)/mt,ms=mt-4m,Ixb、Iyb、Izb分别为忽略质心变化时Jxb、Jyb、Jzb的标称值.三者对时间的微分为
| $ \left\{ \begin{array}{l} {{\dot J}_{x{\rm{b}}}} = 2{m_\text{r}}\left( {{{\dot d}_3}{d_3} + {{\dot d}_4}{d_4}} \right), \\ {{\dot J}_{y{\rm{b}}}} = 2{m_\text{r}}\left( {{d_1}{{\dot d}_1} + {d_2}{{\dot d}_2}} \right), \\ {{\dot J}_{z{\rm{b}}}} = 2{m_\text{r}}\left( {{{\dot d}_1}{d_1} + {{\dot d}_2}{d_2} + {{\dot d}_3}{d_3} + {{\dot d}_4}{d_4}} \right). \end{array} \right. $ | (5) |
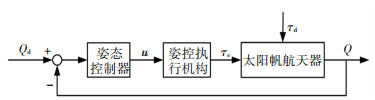
本文控制器设计的目标是对一类采用帆板-滑块执行机构的太阳帆航天器,考虑光压干扰力矩和引力梯度力矩等外部干扰、执行机构导致的转动惯量变化,设计具有较强自适应能力和鲁棒性的姿态控制器;由控制器输出u求解执行机构的运动过程,继而输出控制力矩τc;在τc作用下使太阳帆姿态Q可以快速、准确地跟踪给定的期望姿态Qd.姿态控制系统结构如图 3所示.
|
图 3 太阳帆姿态控制系统结构 Figure 3 Attitude control system for solar sail |
设期望姿态角为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{q}}_{\rm{e}}} = {q_{{\rm{d4}}}}\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_{\rm{d}}}^ \times \mathit{\boldsymbol{q}} - {q_{{\rm{d4}}}}{\mathit{\boldsymbol{q}}_{\rm{d}}}, \\ {q_{{\rm{e4}}}} = \mathit{\boldsymbol{q}}_{\rm{d}}^{\rm{T}}\mathit{\boldsymbol{q}} + {\mathit{\boldsymbol{q}}_4}{q_{{\rm{d4}}}}. \end{array} \right. $ |
| $ {\mathit{\boldsymbol{\omega }}_{\rm{e}}} = \mathit{\boldsymbol{\omega }} - {\mathit{\boldsymbol{\omega }}_{\rm{d}}}. $ |
由式(2)得误差模型为
| $ \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} = - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{\tau }}_d} - \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}}, $ | (6) |
| $ {{\mathit{\boldsymbol{\dot Q}}}_{\rm{e}}} = \frac{1}{2}\left[ \begin{array}{l} \mathit{\boldsymbol{T}}\\ - {\mathit{\boldsymbol{q}}_{\rm{e}}}^{\rm{T}} \end{array} \right]{\mathit{\boldsymbol{\omega }}_{\rm{e}}}. $ | (7) |
式中T=qe4I3+qe×,且‖T‖=1.
为方便控制器设计,首先对太阳帆系统做如下合理假设:
假设1 转动惯量在标称值J0附近变化,其变化量及变化速度有界且已知,即J=J0+ΔJ,‖ΔJ‖≤σJ, σJ≥0,
假设2 外部干扰力矩有界,即‖τd‖≤d,d≥0.
此外给出如下Comparison引理[10]:
引理 函数g,
| $ {{\mathit{\dot V}}_l} \le - a{V_l}\left( t \right) + g\left( t \right), $ |
那么对任意的a有
| $ {{V}_{l}}\le {{\text{e}}^{-a}}{{V}_{l}}\left( 0 \right)+\int\limits_{0}^{t}{{{\text{e}}^{-a\left( t-\tau \right)}}g\left( \tau \right)\text{d}\tau },\forall t\ge 0. $ |
为了使太阳帆姿态控制系统对滑块运动引起的惯量变化具有鲁棒性[11],设计太阳帆滑模姿态控制律.取滑模面:
| $ \mathit{\boldsymbol{s}} = {\mathit{\boldsymbol{\omega }}_{\rm{e}}} + \lambda {\mathit{\boldsymbol{q}}_{\rm{e}}}, \lambda > 0; $ | (8) |
滑模控制器结构为
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{u}}_{\rm{r}}} + {\mathit{\boldsymbol{u}}_{\rm{e}}}, $ | (9) |
式中ur为趋近律,其作用是使系统状态到达滑模面;ue为等效控制律,在系统状态到达滑模面后,使其保持在该流形上.设计ur和ue分别为
| $ {\mathit{\boldsymbol{u}}_{\rm{r}}} = - k\mathit{\boldsymbol{s}} - \left( {b + \hat d + \upsilon } \right){\rm{sign}}\left( \mathit{\boldsymbol{s}} \right), $ | (10) |
| $ {\mathit{\boldsymbol{u}}_{\rm{e}}} = \mathit{\boldsymbol{\omega }} \times {\mathit{\boldsymbol{J}}_0}\mathit{\boldsymbol{\omega + }}{\mathit{\boldsymbol{J}}_0}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} - \lambda {\mathit{\boldsymbol{J}}_0}{{\mathit{\boldsymbol{\dot q}}}_{\rm{e}}}. $ | (11) |
其中:b=σJ(
受投影算法启发,设计自适应律
| $ \dot {\hat d} = \left\{ {\begin{array}{*{20}{c}} {\frac{1}{\eta }\left\| \mathit{\boldsymbol{s}} \right\|, }&{\left\| \mathit{\boldsymbol{s}} \right\| > {s_{\rm{e}}};}\\ {0, }&{\left\| \mathit{\boldsymbol{s}} \right\| \le {s_{\rm{e}}}.} \end{array}} \right. $ | (12) |
定理 考虑式(6)、(7)描述的系统,若满足假设1和假设2,在控制律(9)~(12)的作用下,
姿态误差qe稳定,且‖qe‖≤
证明 设
| $ V = \frac{1}{2}\left( {{s^{\rm{T}}}Js + \eta {{\tilde d}^2}} \right), $ |
对其微分有
| $ \begin{array}{l} \mathit{\dot V} = {s^{\rm{T}}}J\dot s + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{J\dot s + }}\eta \tilde d\dot {\hat d} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{J}}{{\dot \omega }_{\rm{e}}} + \lambda \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \beta }}}_{\rm{e}}}} \right) + \\ \;\;\;\;\frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Js + }}\eta \tilde d\dot {\hat d} = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left( { - \mathit{\boldsymbol{\omega }} \times \mathit{\boldsymbol{J\omega }} + \mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{\tau }}_{\rm{d}}} - } \right.\\ \;\;\;\;\left. {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + \lambda \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \beta }}}_{\rm{e}}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Js}} + \eta \tilde d\dot {\hat d}. \end{array} $ |
当‖s‖>se时, 有
| $ \begin{array}{l} \mathit{\dot V} = {s^{\rm{T}}}\left( { - \mathit{\boldsymbol{\omega }} \times \Delta \mathit{\boldsymbol{J\omega }} - \Delta \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + \lambda \Delta \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \beta }}}_{\rm{e}}} - k\mathit{\boldsymbol{s}} - \left( {b + } \right.} \right.\\ \;\;\;\;\;\left. {\left. {d + \mathit{\boldsymbol{\upsilon }}} \right){\rm{sign}}\left( s \right) + {\tau _{\rm{d}}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\dot Js + \tilde d\left\| \mathit{\boldsymbol{s}} \right\| \le \\ \;\;\;\;\; - k{\left\| \mathit{\boldsymbol{s}} \right\|^2} + \frac{1}{2}\left\| {\mathit{\boldsymbol{\dot J}}} \right\|{\left\| \mathit{\boldsymbol{s}} \right\|^2} + \left( {\left\| {\mathit{\boldsymbol{\dot J}}} \right\| - {\delta _J}} \right)\left\| \mathit{\boldsymbol{s}} \right\| - \\ \;\;\;\;\;\mathit{\boldsymbol{\upsilon }}\left\| \mathit{\boldsymbol{s}} \right\| - \hat d\left\| \mathit{\boldsymbol{s}} \right\| + d\left\| \mathit{\boldsymbol{s}} \right\| + \tilde d\left\| \mathit{\boldsymbol{s}} \right\| \le - k{\left\| \mathit{\boldsymbol{s}} \right\|^2} + \\ \;\;\;\;\;\frac{1}{2}{\delta _j}{\left\| \mathit{\boldsymbol{s}} \right\|^2} - \mathit{\boldsymbol{\upsilon }}\left\| \mathit{\boldsymbol{s}} \right\| + \left( { - \hat d + d} \right)\left\| \mathit{\boldsymbol{s}} \right\| + \tilde d\left\| \mathit{\boldsymbol{s}} \right\| \le \\ \;\;\;\;\; - {k_0}{\left\| \mathit{\boldsymbol{s}} \right\|^2} - \mathit{\boldsymbol{\upsilon }}\left\| \mathit{\boldsymbol{s}} \right\| < 0. \end{array} $ |
可见,在所提控制律作用下,系统状态将沿‖s‖衰减的方向运动,直至‖s‖≤se.
当‖s‖≤se时,取Lyapunov函数
| $ V' = \frac{1}{2}\mathit{\boldsymbol{q}}_{\rm{e}}^{\rm{T}}{\mathit{\boldsymbol{q}}_{\rm{e}}}, $ |
沿系统(6)、(7)对其微分,有
| $ \dot V' = \mathit{\boldsymbol{q}}_{\rm{e}}^{\rm{T}}{{\mathit{\boldsymbol{\dot q}}}_{\rm{e}}} = \frac{1}{2}\mathit{\boldsymbol{q}}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{T}}{\mathit{\boldsymbol{\omega }}_{\rm{e}}}, $ |
滑模面上有s=ωe+λqe,联合T的性质有
| $ \begin{array}{*{20}{c}} {\dot V' = \frac{1}{2}\mathit{\boldsymbol{q}}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{T}}\left( {\mathit{\boldsymbol{s}} - \lambda {\mathit{\boldsymbol{q}}_{\rm{e}}}} \right) \le }\\ { - \frac{\lambda }{2}\mathit{\boldsymbol{q}}_{\rm{e}}^{\rm{T}}{\mathit{\boldsymbol{q}}_{\rm{e}}} + \frac{1}{2}\left\| {{\mathit{\boldsymbol{q}}_{\rm{e}}}} \right\|{s_{\rm{e}}} \le }\\ { - \frac{\lambda }{2}V' + \frac{1}{2}{s_{\rm{e}}}.} \end{array} $ |
由Comparison引理[10]得
| $ {\left\| {{\mathit{\boldsymbol{q}}_{\rm{e}}}} \right\|^2} \le {{\rm{e}}^{ - \lambda /2}}V'\left( 0 \right) + \frac{1}{2}\int_0^t {{{\rm{e}}^{ - \lambda /2\left( {t - \tau } \right)}}{s_{\rm{e}}}{\rm{d}}\tau } , $ |
进一步有
证毕.
2.2 执行机构解算利用姿态控制器输出u可求解帆板的转角与滑块的期望位移,通过帆板的转动和滑块的滑动可获得对应的控制力矩τc,继而实现对姿态系统的控制.由式(3)可知,执行机构工作过程中,4块小帆的角度互相影响,4个滑块的位置也存在耦合关系.对此,本文设计了简单的力矩分配规则,即令γ=γ1=γ3=γ2=γ4,d1=d2,d3=d4,则有
| $ {\mathit{\boldsymbol{\tau }}_{\rm{c}}} = \left[ {\begin{array}{*{20}{c}} { - 8l{P_{\rm{s}}}{A_{\rm{p}}}{{\cos }^2}\left( {\alpha + \gamma } \right)\sin \gamma - 4m/{m_{\rm{t}}}{d_3}{P_{\rm{s}}}A{{\cos }^2}\alpha }\\ {4m/{m_{\rm{t}}}{d_1}{P_{\rm{s}}}A{{\cos }^2}\alpha } \end{array}} \right]. $ | (13) |
对帆板,在太阳帆任务设计中,滚转轴所需控制力矩往往较小,帆板转角也在较小范围内变化.据此,对滚转轴力矩表达式进行小角度线性化,即cosγ=0,sinγ=γ,有τc(1)≈8lPsApγcos2α.记γd为帆板期望转角,则有
| $ {\gamma _{\rm{d}}} \approx \mathit{\boldsymbol{u}}\left( 1 \right)/\left( {8l{P_{\rm{s}}}{A_p}\gamma {{\cos }^2}\alpha } \right), $ |
帆板转角运动过程为
| $ {T_1}\dot \gamma + \gamma = {\gamma _{\rm{d}}}, $ |
式中T1由帆板角度及角速度限幅决定,即
对滑块,令z=[d1d3]T为滑块位置,zd=[d1d d3d]T为其期望位置,由式(13)可得
| $ {\mathit{\boldsymbol{z}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}\left( 3 \right)/\left( {4m/{m_{\rm{t}}}{d_1}{P_{\rm{s}}}A{{\cos }^2}\alpha } \right)}\\ { - \mathit{\boldsymbol{u}}\left( 2 \right)/\left( {4m/{m_{\rm{t}}}{d_3}{P_{\rm{s}}}A{{\cos }^2}\alpha } \right)} \end{array}} \right], $ |
滑块运动采用模型
| $ {T_2}\mathit{\boldsymbol{\dot z}} + \mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{z}}_{\rm{d}}}. $ |
式中T2由最大滑动位置zmax和最大滑动速度żmax决定,即żmax=zmax/T2.
3 数值模拟参考文献[5],本文采用如下太阳帆参数进行数值仿真实验:转动惯量标称值为[6 000 3 000 3 000],Ap=2m2,l=8m,A=1 200 m2,m=2 kg,mt=157 kg.帆板转角和角速度的最大值分别为γmax=80°,
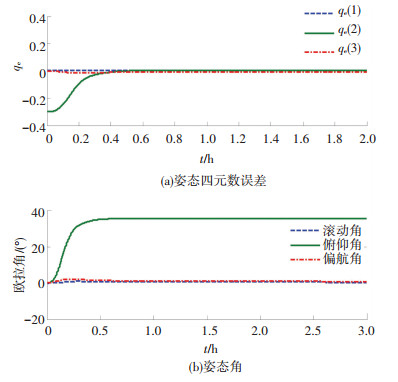
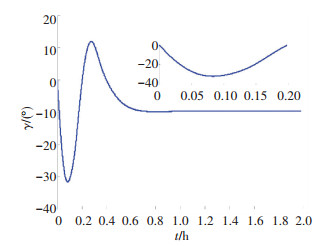
仿真结果如图 4~9所示. 图 4为姿态响应图,由图可知,姿态四元数误差qe趋向于0,太阳帆俯仰角由0°机动至35°时间远小于1 h,机动时间短;角度稳态误差保持在0.01°以内,满足了太阳帆飞行要求. 图 5为4个滑块位移曲线.滑块1、2的最大位移为6.598 m,随着姿态角趋向机动位置,逐渐稳定于3.925 m处以抵抗偏航轴所受干扰.滑块3、4的运动提供了俯仰角机动所需力矩,二者最大位移均为18.442 m;姿态误差收敛后,滑块3、4位置均保持在1.962 m处. 图 6为帆板转动过程,帆板转角最大幅度为31.693°,并稳定在-9.666°以消除滚转轴所受干扰. 图 5、6中的子图还分别显示了滑块和帆板在时间初始段的响应,可见二者运动轨迹平滑无大幅跃变,在实际应用中易于实现.
|
图 4 姿态响应 Figure 4 Response of attitude |

|
图 5 滑块位置 Figure 5 Positions of masses |
|
图 6 帆板角度 Figure 6 Angle of rotating panel |

|
图 7 干扰上界估计 Figure 7 Estimation of disturbance upper bounds |
|
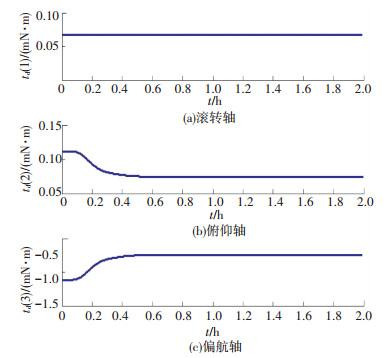
图 8 干扰力矩曲线 Figure 8 Disturbance torque curves |
|
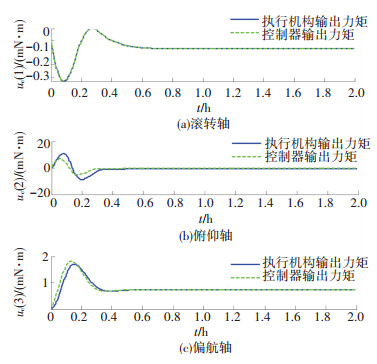
图 9 力矩 Figure 9 Torques |
图 7给出了干扰力矩上界的估计结果图,图 8为干扰力矩示意图,滚动轴干扰力矩为常值,俯仰轴和偏航轴干扰力矩随俯仰角变化. 图 9为控制器输出u和执行机构输出的控制力矩τc. U为执行机构的期望输入,3轴最大幅值分别为0.327 6、6.486、1.827 mN·m,皆在执行机构可实现范围内.此外,各轴控制量曲线缓和,自适应律的加入在抑制干扰的同时,也有效地抑制了滑模控制器中存在的抖振现象.通过滑块位移和帆板转动可求得实际控制力矩τc,如图中实线所示.可见,通过图 5、6所示的帆板转动和滑块滑动,执行机构较好地实现了所需控制力矩.
综上,所提控制策略在考虑光压力矩干扰、引力梯度干扰和转动惯量变化的情况下,有效地实现了太阳帆三轴姿态控制.
4 结论本文采用了一种新型帆板-滑块结构作为太阳帆航天器的姿控执行机构,在此结构下研究了太阳帆姿态控制律设计与实现问题.针对滑块滑动致使太阳帆转动惯量变化问题,设计了鲁棒滑模姿态控制器.同时,考虑了光压力矩和引力梯度力矩两种干扰,设计了自适应律对干扰上界进行估计.最后,解算执行机构,实现所提控制律.仿真结果表明,所提控制方法可使太阳帆姿态较快机动至期望位置,并使控制力矩、帆板角度和滑块位移均保持在适当的幅值范围内,易于实现.
| [1] |
TSUDA Y, MARI O, FUNASE R, et al. Achievement of IKAROS—Japanese deep space solar sail demonstration mission[J]. Acta Astronautica, 2013, 82(2): 183. DOI:10.1016/j.actaastro.2012.03.032 |
| [2] |
MU Junshan, GONG Shengping, LI Junfeng. Coupled control of reflectivity modulated solar sail for GeoSail formation flying[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(4): 740. DOI:10.2514/1.G000117 |
| [3] |
MCKAY R, MACDOALD M, BIGGS J, et al. Survey of highly non-Keplerian orbits with low-thrust propulsion[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(3): 645. DOI:10.2514/1.52133 |
| [4] |
罗超, 郑建华. 采用滑块和RSB的太阳帆姿态控制[J]. 哈尔滨工业大学学报, 2011, 43(3): 95. LUO Chao, ZHENG Jianhua. Solar-sail attitude control based on moving masses and roll stabilizer bars[J]. Journal of Harbin Institute of Technology, 2011, 43(3): 95. |
| [5] |
ADELI S N, LAPPAS V J, WIE B. A scalable bus-based attitude control system forsolar sails[J]. Advances in Space Research, 2011, 48: 1836. DOI:10.1016/j.asr.2011.08.024 |
| [6] |
ROMAGNOLI D, OEHLSCHLAGEL T. High performance two degrees of freedom attitude control for solar sails[J]. Advances in Space Research, 2011, 48(11): 1869. DOI:10.1016/j.asr.2011.04.027 |
| [7] |
张震亚, 韩艳铧, 贾杰. 带移动滑块的太阳帆航天器动力学建模与姿态控制[J]. 航天控制, 2014, 32(5): 29. ZHANG Zhenya, HAN Yanhua, JIA Jie. Dynamics modeling and attitude control of moving-mass based solar sail spacecraft[J]. Aerospace Control, 2014, 32(5): 29. DOI:10.3969/j.issn.1006-3242.2014.05.006 |
| [8] |
ELDAD O, LIGHTSEY G. Propellantless attitude control of a nonplanar solar sail[J]. Journal of Guidance and Dynamics, 2015, 38(8): 1531. DOI:10.2514/1.G001135 |
| [9] |
CHOI M, DAMAREN C J. Structuraldynamics and attitude control of a solar sail using tip vanes[J]. Journal of Spacecraft and Rockets, 2015, 52(6): 1666. |
| [10] |
DING Zhengtao. Nonlinear andadaptive control systems[M]. London: The Institution of Engineering and Technology, 2013: 50.
|
| [11] |
DONG Qi, ZONG Qun, TIAN Bailing, et al. Adaptive-gain multivariable super-twisting sliding mode control for reentry RLV with torque perturbation[J]. International Journal of Robust and Nonli-near Control, 2017, 27(4): 620. DOI:10.1002/rnc.v27.4 |
 2018, Vol. 50
2018, Vol. 50


