2. 中国电子科技集团公司 电子科学研究院, 北京 100041
2. China Academy of Electronics and Information Technology, Beijing100041, China
近年来,由于巨大的军用和民用价值,固定翼无人机的研究得到了各界广泛的关注.无论是单机控制还是机群控制,固定翼无人机控制器的设计都面临着许多挑战,比如无人机内部模型不确定和复杂空气动力学特征带来的外部扰动等问题.正是这些难题的存在,固定翼无人机控制器需要更高的精确性和鲁棒性.因此,一个好的控制方案可以给现有的无人机技术带来巨大的提升.
近些年,许多方法被应用于无人机飞行控制中,例如:PID控制、动态逆、反步法和神经网络控制等.文献[1]针对旋翼无人机设计PID控制器并用神经网络对其扰动进行观测.文献[2]利用反步法对小型无人机进行轨迹跟踪控制.文献[3]针对四旋翼无人机提出近似自适应鲁棒控制器,并用CMAC(cerebellar model articulation controller)方法进行非线性估计.文献[4]利用自适应神经网络对可倾斜旋翼无人机设计轨迹跟踪控制器.文献[5]首先建立无人机四元数模型,然后设计反步控制器进行轨迹跟踪控制并证明了该方法的一致渐近稳定性.文献[6]针对固定翼无人机姿态和速度控制中存在模型不确定和外界干扰问题,设计了基于扩张观测器的反步控制器抑制系统的扰动并提高了无人机的控制性能.虽然这些线性和非线性控制方法都很好地运用在无人机的控制当中,然而在现实飞行中无人机经常受到气动变化、负载变化等干扰的影响,使得控制难度大大提升.目前,滑模控制仍然是一种有效的控制方法解决带有外部扰动以及不确定的非线性问题[7-8].滑模控制被运用在许多领域当中,如高超声速飞行器控制[9-12]及卫星姿态控[13].由于固定翼无人机模型在简化过程中存在较大的不确定、未建模特性以及外界扰动,这使得本身具有强鲁棒性的滑模控制仍然是其主要的选择.
本文基于自适应超螺旋滑模,设计一种新型的自适应多变量干扰观测器对模型中干扰进行有限时间在线、实时、精确估计.相比于传统的干扰观测器,干扰估计的速度与精度明显提升.通过结合自适应多变量干扰观测器与多变量超螺旋滑模控制器,提出了一种有限时间综合控制策略,并将其运用在固定翼无人机的姿态与速度跟踪控制上,获得了满意的结果.在仿真阶段,针对无人机不同的飞行状态分别进行数值仿真,仿真结果表明该综合控制策略的有效性,并为实际的无人机飞行控制提供了有力的支撑.
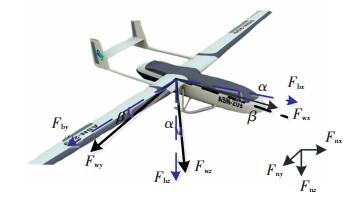
1 无人机建模(UAV modeling)无人机姿态运动涉及惯性坐标系Fn、机体坐标系Fb、气流坐标系Fw. 3个坐标系的关系如图 1所示,其中α为无人机的攻角;β为无人机的侧滑角.在无人机姿态建模过程中,采用基于四元数的姿态误差模型,该方法可以有效的避免欧拉角在描述姿态时存在的奇点问题和复杂的三角运算.
|
图 1 固定翼无人机模型及坐标系 Figure 1 Model and coordinate system of fixed-wing UAV |
无人机动力学方程为
| $ {{\mathit{\boldsymbol{\dot v}}}^{\rm{b}}} = \frac{1}{m}{\mathit{\boldsymbol{f}}_{{\rm{thrust}}}} + \frac{1}{m}\mathit{\boldsymbol{R}}_{\rm{w}}^{\rm{b}}\mathit{\boldsymbol{f}}_{{\rm{aero}}}^{\rm{w}} + \mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}{\mathit{\boldsymbol{g}}^{\rm{n}}} - S\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right){\mathit{\boldsymbol{v}}^{\rm{b}}}, $ | (1) |
| $ \mathit{\boldsymbol{J\dot \omega }}_{\rm{n}}^{\rm{b}} = - \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right)\mathit{\boldsymbol{J\omega }}_{\rm{n}}^{\rm{b}} + \mathit{\boldsymbol{\tau }}, $ | (2) |
| $ {{\mathit{\boldsymbol{\dot q}}}_{{\rm{n,b}}}} = \frac{1}{2}{\mathit{\boldsymbol{R}}_{{\rm{qn}}}}\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}. $ | (3) |
式中:vb为无人机机体坐标系下的速度矢量;Rbn为机体坐标系到惯性坐标系的旋转矩阵;m为无人机的质量;faerow为无人机在气流坐标系所受的气动力;Rwb为气流坐标系到机体坐标系的旋转矩阵;fthrust=[T 0 0]T,其中T为无人机推力;gn为惯性坐标系下的重力加速度;
| $ \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right) = \left[ {\begin{array}{*{20}{c}} 0&{ - {\omega _{\rm{r}}}}&{{\omega _{\rm{q}}}}\\ {{\omega _{\rm{r}}}}&0&{ - {\omega _{\rm{p}}}}\\ { - {\omega _{\rm{q}}}}&{{\omega _{\rm{p}}}}&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{R}}_{\rm{b}}^{\rm{w}} = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\sin \beta }&{\sin \alpha \cos \beta }\\ { - \cos \alpha \sin \beta }&{\cos \beta }&{ - \sin \alpha \sin \beta }\\ { - \sin \alpha }&0&{\cos \alpha } \end{array}} \right], $ |
| $ \mathit{\boldsymbol{f}}_{{\rm{aero}}}^{\rm{w}} = \frac{1}{2}\rho {V_{\rm{a}}}^2b\left[ {\begin{array}{*{20}{c}} { - {C_{\rm{D}}}}\\ {{C_{\rm{Y}}}}\\ { - {C_{\rm{L}}}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{R}}_{{\rm{qn}}}} = \left[ {\begin{array}{*{20}{c}} { - {q_1}}&{ - {q_2}}&{ - {q_3}}\\ {{q_0}}&{ - {q_3}}&{{q_2}}\\ {{q_3}}&{{q_0}}&{ - {q_1}}\\ { - {q_2}}&{{q_1}}&{{q_0}} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{q}}_{{\rm{n}},{\rm{b}}}} = \left[ {\begin{array}{*{20}{c}} {\cos \left( {\frac{\vartheta }{2}} \right)}&{{k^{\rm{T}}}\sin \left( {\frac{\vartheta }{2}} \right)} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{q_0}}&{{q_1}}&{{q_2}}&{{q_3}} \end{array}} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{R}}_{\rm{b}}^{\rm{n}} = \mathit{\boldsymbol{I}} + 2\cos \left( {\frac{\vartheta }{2}} \right)\mathit{\boldsymbol{S}}\left( {{k^{\rm{T}}}\sin \left( {\frac{\vartheta }{2}} \right)} \right) + 2{\mathit{\boldsymbol{S}}^2}\left( {{k^{\rm{T}}}\sin \left( {\frac{\vartheta }{2}} \right)} \right). $ |
其中:b为无人机翼面积, ρ为空气密度, 速度标量Va=‖vrb‖, vrb为无人机相对于风速的速度, ϑ为围绕单位向量k的转动角, 且四元数满足q02+q12+q22+q32=1, I为单位矩阵, CD、CY、CL均为气动力参数,CD=CD0+KCL2,CY=Cββ,CL=CL0+CLαα.
无人机依靠气动力飞行,无人机相对于风速的速度vrb可以定义为
| $ \mathit{\boldsymbol{v}}_{\rm{r}}^{\rm{b}} = {\mathit{\boldsymbol{v}}^{\rm{b}}} - \mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}\mathit{\boldsymbol{v}}_{\rm{w}}^{\rm{n}}. $ | (4) |
其中vwn为惯性坐标系下风速度矢量.定义vrb=[ur vr wr]T,由此得到攻角α, 侧滑角β为
| $ \alpha = {\tan ^{ - 1}}\left( {\frac{{{w_{\rm{r}}}}}{{{u_{\rm{r}}}}}} \right),\;\;\;\;\beta = {\sin ^{ - 1}}\left( {\frac{{{v_{\rm{r}}}}}{{\left\| {v_{\rm{r}}^{\rm{b}}} \right\|}}} \right). $ |
对式(4)求微分,得
| $ \mathit{\boldsymbol{\dot v}}_{\rm{r}}^{\rm{b}} = {{\mathit{\boldsymbol{\dot v}}}^{\rm{b}}} + \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right)\mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}\mathit{\boldsymbol{v}}_{\rm{w}}^{\rm{n}}. $ | (5) |
把式(5)代入式(1),可得无人机速度与气流速度的相对速度的动力学方程为
| $ \begin{array}{l} \mathit{\boldsymbol{\dot v}}_{\rm{r}}^{\rm{b}} = \frac{1}{m}{\mathit{\boldsymbol{f}}_{{\rm{thrust}}}} + \frac{1}{m}\mathit{\boldsymbol{R}}_{\rm{w}}^{\rm{b}}\mathit{\boldsymbol{f}}_{{\rm{aero}}}^{\rm{w}} + \mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}{\mathit{\boldsymbol{g}}^{\rm{n}}} - \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right){\mathit{\boldsymbol{v}}^{\rm{b}}} + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right)\mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}\mathit{\boldsymbol{v}}_{\rm{w}}^{\rm{n}} + \Delta \mathit{\boldsymbol{d}}. \end{array} $ | (6) |
式中Δd为飞行过程中受到的外部干扰.
设目标姿态四元数qd=[±1 0 0 0]T,其中[1 0 0 0]T和[-1 0 0 0]T的数学表示不同,但其表示的物理意义式相同的.由于采用四元数qd表示无人机姿态具有双值性,对控制器的设计会带来不必要的麻烦,因此本文采用姿态误差四元数qe,既可解决双值性所产生的问题.
| $ {\mathit{\boldsymbol{q}}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {1 \mp {\eta _{{\rm{d,b}}}}}\\ {{\mathit{\boldsymbol{\varepsilon }}_{{\rm{d,b}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {1 \mp {q_{{\rm{b,0}}}}}\\ {{q_{{\rm{b,1}}}}}\\ {{q_{{\rm{b,2}}}}}\\ {{q_{{\rm{b,3}}}}} \end{array}} \right]. $ | (7) |
即当qe=0时表示无人机达到所期望的姿态位置.无人机姿态动力学方程可表示为
| $ {{\mathit{\boldsymbol{\dot q}}}_{\rm{e}}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} { - {q_{{\rm{b1}}}}}&{ - {q_{{\rm{b2}}}}}&{ - {q_{{\rm{b3}}}}}\\ {{q_{{\rm{b0}}}}}&{ - {q_{{\rm{b3}}}}}&{{q_{{\rm{b2}}}}}\\ {{q_{{\rm{b3}}}}}&{{q_{{\rm{b0}}}}}&{ - {q_{{\rm{b1}}}}}\\ { - {q_{{\rm{b2}}}}}&{{q_{{\rm{b1}}}}}&{{q_{{\rm{b0}}}}} \end{array}} \right]{\mathit{\boldsymbol{\omega }}_{\rm{e}}}, $ | (8) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} = - \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right)\mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right) - }\\ {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + \mathit{\boldsymbol{\tau }} + \Delta \mathit{\boldsymbol{\tau }}.} \end{array} $ | (9) |
式中速度误差ωe=ωnb-ωd, ωd为期望角速度, Δτ为飞行过程中外部扰动.
方程(6)与方程(8)、(9)共同组成了固定翼无人机速度与姿态的控制模型.
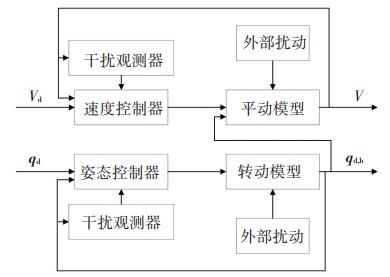
2 控制器设计 2.1 控制目标根据固定翼无人机模型,针对无人机的平动环节和转动环节分别设计控制器,其中转动环节控制无人机的姿态qd, b跟踪上给定姿态qd,即qe=0, 角速度ωnb跟踪期望角速度ωd, 即ωe=0.平动环节控制无人机水平速度ur收敛到期望值ur, d.控制框图如图 2所示.
|
图 2 控制框图 Figure 2 Control block diagram |
考虑到如下多输入多输出非线性系统,假设综合扰动Δ有界.设计自适应滑模干扰观测器,对不确定Δ进行估计.
| $ \mathit{\boldsymbol{\dot x}} = f\left( {\mathit{\boldsymbol{x}},t} \right) + g\left( {\mathit{\boldsymbol{x}},t} \right)\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}, $ | (10) |
式中
通过设计自适应超螺旋滑模观测器估计综合不确定量Δ, 使
| $ \mathit{\boldsymbol{\dot w}} = f\left( {\mathit{\boldsymbol{x}},t} \right) + g\left( {\mathit{\boldsymbol{x}},t} \right)\mathit{\boldsymbol{u}} + \mathit{\boldsymbol{\nu}}. $ | (11) |
定义滑模变量
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{x}} - \mathit{\boldsymbol{w}}, $ | (12) |
对式(12)求微分,得
| $ \mathit{\boldsymbol{\dot s}} = \mathit{\boldsymbol{\dot x}} - \mathit{\boldsymbol{\dot w}} = \mathit{\boldsymbol{ \boldsymbol{\varDelta} }} - \mathit{\boldsymbol{\nu}}, $ | (13) |
设计自适应超螺旋滑模观测器为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\nu}} = {\alpha _1}\frac{\mathit{\boldsymbol{s}}}{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^{\frac{1}{2}}}}} + \mathit{\boldsymbol{\eta }},\\ \mathit{\boldsymbol{\dot\eta }} = {\beta _1}\frac{\mathit{\boldsymbol{s}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}}. \end{array} \right. $ | (14) |
其中自适应增益α1,β1如下分别为
| $ {{\dot \alpha }_1} = \left\{ \begin{array}{l} {\omega _1}\sqrt {\frac{{{\gamma _1}}}{2}} ,\;\;\;\;\left\| \mathit{\boldsymbol{s}} \right\| > {\delta _{\rm{T}}};\\ 0,\;\;\;\;\left\| \mathit{\boldsymbol{s}} \right\| \le {\delta _{\rm{T}}}. \end{array} \right. $ | (15) |
| $ {\beta _1} = {\varepsilon _1}{\alpha _1}. $ | (16) |
式中ω1、γ1、ε1为任意正数,δT为任意小的阈值.
把式(14)代入式(13)可得
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot s}} = - {\alpha _1}\frac{\mathit{\boldsymbol{s}}}{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^{\frac{1}{2}}}}} + {\mathit{\boldsymbol{\eta }}_1},\\ {{\mathit{\boldsymbol{\dot \eta }}}_1} = - {\beta _1}\frac{\mathit{\boldsymbol{s}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}} + \mathit{\boldsymbol{ \boldsymbol{\dot \varDelta} }}. \end{array} \right. $ | (17) |
定理1 在假设
证明 考虑系统(17),设计Lyapunov函数
| $ {V_s} = {V_0} + \frac{1}{{2{\gamma _1}}}{\left( {{\alpha _1} - \alpha _1^ * } \right)^2} + \frac{1}{{2{\gamma _3}}}{\left( {{\beta _1} - \beta _1^ * } \right)^2}, $ | (18) |
其中α1*>0,β1*>0,γ3为某个大于0的常数,
| $ \begin{array}{*{20}{c}} {{V_0} = \left( {\lambda + 4\varepsilon _1^2} \right)\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} + \mathit{\boldsymbol{z}}_2^{\rm{T}}{\mathit{\boldsymbol{z}}_2} - }\\ {2{\varepsilon _1}\left( {\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_2} + \mathit{\boldsymbol{z}}_2^{\rm{T}}{\mathit{\boldsymbol{z}}_1}} \right) = {\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{Pz}}.} \end{array} $ | (19) |
定义
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {\lambda + 4\varepsilon _1^2}&{ - {\varepsilon _1}}\\ { - {\varepsilon _1}}&1 \end{array}} \right]. $ |
可以看出,若λ>0且ε1为实数,则矩阵P正定.
对式(18)求微分,可得
| $ {{\dot V}_s} = {{\dot V}_0} + \frac{1}{{{\gamma _1}}}\left( {{\alpha _1} - \alpha _1^ * } \right){{\dot \alpha }_1} + \frac{1}{{{\gamma _3}}}\left( {{\beta _1} - \beta _1^ * } \right){{\dot \beta }_1}, $ | (20) |
其中
| $ {{\dot V}_0} = {{\mathit{\boldsymbol{\dot z}}}^{\rm{T}}}\mathit{\boldsymbol{Pz}} + {\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{P\dot z}} - \frac{1}{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^{\frac{1}{2}}}}}{\mathit{\boldsymbol{z}}^{\rm{T}}}\mathit{\boldsymbol{Qz}}, $ | (21) |
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {\lambda {\alpha _1} + {\varepsilon _1}\left( {{\varepsilon _1}{\alpha _1} - {\beta _1} + 2{\varepsilon _1}\delta } \right)}&{\frac{1}{2}\left( {{\beta _1} - {\varepsilon _1}{\alpha _1} - \lambda - \varepsilon _1^2} \right) - \delta }\\ {\frac{1}{2}\left( {{\beta _1} - {\varepsilon _1}{\alpha _1} - \lambda - \varepsilon _1^2} \right) - \delta }&{2{\varepsilon _1}} \end{array}} \right]. $ |
为了保证Q正定,可以得到
| $ {\beta _1} = {\varepsilon _1}{\alpha _1}. $ | (22) |
如果
| $ {\alpha _1} > - \frac{{{\varepsilon _1}\left( {4\delta + 1} \right)}}{{2\lambda }} + \frac{{{{\left( {2\delta + \lambda + \varepsilon _1^2} \right)}^2}}}{{6{\varepsilon _1}\lambda }}, $ | (23) |
可以得到Q的最小特征根为
| $ {\lambda _{\min }}\left( \mathit{\boldsymbol{Q}} \right) \ge {\varepsilon _1}. $ | (24) |
结合式(21)~(23)可以得到
| $ {{\dot V}_0} \le - \frac{{{\varepsilon _1}\lambda _{\min }^{\frac{1}{2}}\left( \mathit{\boldsymbol{P}} \right)}}{{2{\lambda _{\min }}\left( \mathit{\boldsymbol{P}} \right)}}V_0^{\frac{1}{2}}. $ | (25) |
把式(25)代入式(20)可得
| $ \begin{array}{l} {{\dot V}_s} \le - \frac{{{\varepsilon _1}\lambda _{\min }^{\frac{1}{2}}\left( \mathit{\boldsymbol{P}} \right)}}{{2{\lambda _{\min }}\left( \mathit{\boldsymbol{P}} \right)}}V_0^{\frac{1}{2}} - \frac{{{\omega _1}}}{{\sqrt {2{\gamma _1}} }}\left| {{\alpha _1} - \alpha _1^ * } \right| - \\ \;\;\;\;\;\;\frac{{{\omega _3}}}{{\sqrt {2{\gamma _3}} }}\left| {{\beta _1} - \beta _1^ * } \right| + \frac{1}{{{\gamma _1}}}\left( {{\alpha _1} - \alpha _1^ * } \right){{\dot \alpha }_1} + \\ \;\;\;\;\;\;\frac{1}{{{\gamma _3}}}\left( {{\beta _1} - \beta _1^ * } \right){{\dot \beta }_1} + \frac{{{\omega _1}}}{{\sqrt {2{\gamma _1}} }}\left| {{\alpha _1} - \alpha _1^ * } \right| + \\ \;\;\;\;\;\;\frac{{{\omega _3}}}{{\sqrt {2{\gamma _3}} }}\left| {{\beta _1} - \beta _1^ * } \right|. \end{array} $ | (26) |
根据柯西不等式可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_s} \le - {\sigma _0}\sqrt {{V_s}} - \left| {{\alpha _1} - \alpha _1^ * } \right|\left( {\frac{1}{{{\gamma _1}}}{{\dot \alpha }_1} - \frac{{{\omega _1}}}{{\sqrt {2{\gamma _1}} }}} \right) - }\\ {\left| {{\beta _1} - \beta _1^ * } \right|\left( {\frac{1}{{{\gamma _3}}}{{\dot \beta }_1} - \frac{{{\omega _3}}}{{\sqrt {2{\gamma _3}} }}} \right),} \end{array} $ | (27) |
式中
为了使系统有限时间收敛,令
| $ \begin{array}{*{20}{c}} { - \left| {{\alpha _1} - \alpha _1^ * } \right|\left( {\frac{1}{{{\gamma _1}}}{{\dot \alpha }_1} - \frac{{{\omega _1}}}{{\sqrt {2{\gamma _1}} }}} \right) - }\\ {\left| {{\beta _1} - \beta _1^ * } \right|\left( {\frac{1}{{{\gamma _3}}}{{\dot \beta }_1} - \frac{{{\omega _3}}}{{\sqrt {2{\gamma _3}} }}} \right) = 0,} \end{array} $ |
由此可以得到自适应增益为
| $ \left\{ \begin{array}{l} {{\dot \alpha }_1} = {\omega _1}\sqrt {\frac{{{\gamma _1}}}{2}} ,\\ {{\dot \beta }_1} = {\omega _3}\sqrt {\frac{{{\gamma _3}}}{2}} = {\varepsilon _1}{{\dot \alpha }_1}. \end{array} \right. $ | (28) |
式中
根据式(27)、(28),可以得到滑模变量s及其导数
| $ {t_s} \le \frac{{2{V^{\frac{1}{2}}}\left( 0 \right)}}{{{\sigma _0}}}. $ | (29) |
定理1得证.
2.3 转动环节控制器设计首先,考虑系统(8),设计虚拟控制指令ωev,使得误差四元数qe趋近于0,根据四元数的性质,只需跟踪后3项即可完成跟踪目标,即eq=[qb, 1 qb, 2 qb, 3]T.因此,系统(8)可以重写为
| $ {{\mathit{\boldsymbol{\dot e}}}_q} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {{q_{{\rm{b}},0}}}&{ - {q_{{\rm{b}},3}}}&{{q_{{\rm{b}},2}}}\\ {{q_{{\rm{b}},3}}}&{{q_{{\rm{b}},0}}}&{ - {q_{{\rm{b}},1}}}\\ { - {q_{{\rm{b}},2}}}&{{q_{{\rm{b}},1}}}&{{q_{{\rm{b}},0}}} \end{array}} \right]{\mathit{\boldsymbol{\omega }}_{{\rm{ev}}}} = \frac{1}{2}{\mathit{\boldsymbol{R}}_q}{\mathit{\boldsymbol{\omega }}_{{\rm{ev}}}}, $ | (30) |
式中ωev=[ωev, 1 ωev, 2 ωev, 3]T为虚拟控制角速度误差指令.
定义快速终端滑模面为
| $ {\mathit{\boldsymbol{s}}_q} = {\mathit{\boldsymbol{e}}_q} + {k_q}\int_0^t {\left[ {{{\left| {{\mathit{\boldsymbol{e}}_q}} \right|}^{{\gamma _{q1}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right) + {{\left| {{\mathit{\boldsymbol{e}}_q}} \right|}^{{\gamma _{q2}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right)} \right]{\rm{d}}\tau } . $ | (31) |
式中sign(·)为符号函数,kq>0,常量γq1>1,0 < γq2 < 1,
| $ {\left| {{\mathit{\boldsymbol{e}}_q}} \right|^{{\gamma _{q * }}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right) = \left[ {\begin{array}{*{20}{c}} {{{\left| {{q_{{\rm{b}},1}}} \right|}^{{\gamma _{q * }}}}{\rm{sign}}\left( {{q_{{\rm{b}},1}}} \right)}\\ {{{\left| {{q_{{\rm{b}},2}}} \right|}^{{\gamma _{q * }}}}{\rm{sign}}\left( {{q_{{\rm{b}},2}}} \right)}\\ {{{\left| {{q_{{\rm{b}},3}}} \right|}^{{\gamma _{q * }}}}{\rm{sign}}\left( {{q_{{\rm{b}},3}}} \right)} \end{array}} \right]. $ |
对式(31)求微分, 得
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot s}}}_q} = \frac{1}{2}{R_q}{\mathit{\boldsymbol{\omega }}_{{\rm{ev}}}} + {k_q}\left[ {{{\left| {{\mathit{\boldsymbol{e}}_q}} \right|}^{{\gamma _{q1}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right) + } \right.}\\ {\left. {{{\left| {{\mathit{\boldsymbol{e}}_q}} \right|}^{{\gamma _{q2}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right)} \right].} \end{array} $ | (32) |
为了使跟踪轨迹快速地达到滑模面,并减小抖震现象,提出一种多变量超螺旋滑模算法,即
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot s}} = - {k_1}\frac{\mathit{\boldsymbol{s}}}{{{{\left\| \mathit{\boldsymbol{s}} \right\|}^{\frac{1}{2}}}}} - {k_2}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{\tilde \omega }},\\ \mathit{\boldsymbol{\dot {\tilde \omega} }} = - {k_3}\frac{\mathit{\boldsymbol{s}}}{{\left\| \mathit{\boldsymbol{s}} \right\|}} - {k_4}s. \end{array} \right. $ | (33) |
把式(33)代入式(32),得到基于超螺旋滑模算法的姿态控制律为
| $ \begin{array}{l} {\mathit{\boldsymbol{\omega }}_{{\rm{ev}}}} = 2{\mathit{\boldsymbol{R}}_q}^{ - 1}\left\{ { - {k_{q1}}\frac{{{\mathit{\boldsymbol{s}}_q}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_q}} \right\|}^{\frac{1}{2}}}}} - {k_{q2}}{s_q} + {{\mathit{\boldsymbol{\tilde \omega }}}_q} - } \right.\\ \;\;\;\;\;\;\left. {{k_q}\left[ {{{\left| {{\mathit{\boldsymbol{e}}_q}} \right|}^{{\gamma _{q1}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right) + {{\left| {{\mathit{\boldsymbol{e}}_q}} \right|}^{{\gamma _{q2}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_q}} \right)} \right]} \right\},\\ \;\;\;\;\;\;{{\mathit{\boldsymbol{\dot {\tilde \omega} }}}_q} = - {k_{q3}}\frac{{{\mathit{\boldsymbol{s}}_q}}}{{\left\| {{\mathit{\boldsymbol{s}}_q}} \right\|}} - {k_{q4}}{\mathit{\boldsymbol{s}}_q}. \end{array} $ | (34) |
然后,设计控制器τ,使得角速度误差跟踪上期望的虚拟角速度误差为
| $ {\mathit{\boldsymbol{e}}_\omega } = {\mathit{\boldsymbol{\omega }}_{\rm{e}}} - {\mathit{\boldsymbol{\omega }}_{{\rm{ev}}}}. $ | (35) |
eω的动力学方程为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot e}}}_\omega } = {{\mathit{\boldsymbol{\dot \omega }}}_{\rm{e}}} - {{\mathit{\boldsymbol{\dot \omega }}}_{{\rm{ev}}}} = {\mathit{\boldsymbol{J}}^{ - 1}}\left[ { - \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right)\mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + \mathit{\boldsymbol{\tau }}} \right] - {{\mathit{\boldsymbol{\dot \omega }}}_{{\rm{ev}}}} + \Delta \mathit{\boldsymbol{\tau }}. \end{array} $ | (36) |
在实际中难以得到虚拟控制的导数
控制器设计采用与上文相似的方法,定义快速终端滑模面为
| $ {\mathit{\boldsymbol{s}}_\omega } = {\mathit{\boldsymbol{e}}_\omega } + {k_\omega }\int_0^t {{{\left| {{\mathit{\boldsymbol{e}}_\omega }} \right|}^{{\gamma _{\omega 1}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_\omega }} \right) + {{\left| {{\mathit{\boldsymbol{e}}_\omega }} \right|}^{{\gamma _{\omega 2}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_\omega }} \right){\rm{d}}\tau } . $ | (37) |
对式(37)求导,得
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_\omega } = {\mathit{\boldsymbol{J}}^{ - 1}}\left[ { - \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right)\mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right) - \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + \mathit{\boldsymbol{\tau }}} \right] + \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{\eta\tau }} - {{\mathit{\boldsymbol{\dot \omega }}}_{{\rm{ev}}}} + {k_\omega } \times \left[ {{{\left| {{\mathit{\boldsymbol{e}}_\omega }} \right|}^{{\gamma _{\omega 1}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_\omega }} \right) + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left| {{\mathit{\boldsymbol{e}}_\omega }} \right|}^{{\gamma _{\omega 2}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_\omega }} \right)} \right]. \end{array} $ | (38) |
将式(33)代入式(38),得滑模控制率为
| $ \begin{array}{l} \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right)\mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right) + \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + \mathit{\boldsymbol{J}}\left\{ {{{\mathit{\boldsymbol{\dot \omega }}}_{{\rm{ev}}}} - } \right.\\ \;\;\;\;\;\;{\mathit{\boldsymbol{k}}_{\omega 1}}\frac{{{\mathit{\boldsymbol{s}}_\omega }}}{{{{\left\| {{\mathit{\boldsymbol{s}}_\omega }} \right\|}^{\frac{1}{2}}}}} - {k_{\omega 2}}{\mathit{\boldsymbol{s}}_\omega } + {{\mathit{\boldsymbol{\tilde \omega }}}_\omega } - \mathit{\boldsymbol{\eta\tau }} - {k_\omega } \times \\ \;\;\;\;\;\;\left. {\left[ {{{\left| {{\mathit{\boldsymbol{e}}_\omega }} \right|}^{{\gamma _{\omega 1}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_\omega }} \right) + {{\left| {{\mathit{\boldsymbol{e}}_\omega }} \right|}^{{\gamma _{\omega 2}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{e}}_\omega }} \right)} \right.} \right\}, \end{array} $ | (39) |
其中
根据系统(6),设计固定翼无人机推力T,使得速度ur跟踪期望指令ur, d.
定义跟踪误差为
| $ {e_{\rm{r}}} = {u_{\rm{r}}} - {u_{{\rm{r,d}}}}. $ | (40) |
快速终端滑模面为
| $ \begin{array}{l} {s_{\rm{r}}} = {e_{\rm{r}}} + {k_{\rm{r}}}\int_0^t {{{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}1}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right)} + \\ \;\;\;\;\;\;\;\;\;{\left| {{e_{\rm{r}}}} \right|^{{\gamma _{{\rm{r}}2}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right){\rm{d}}\tau , \end{array} $ | (41) |
式中kr>0,常量γr1>1,0 < γr2 < 1.
对式(41)求微分, 得
| $ \begin{array}{l} {{\dot s}_{\rm{r}}} = {{\dot e}_{\rm{r}}} + {k_{\rm{r}}}\left[ {{{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}1}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right) + {{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}2}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right)} \right] = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]\left[ {\frac{1}{m}{f_{{\rm{thrust}}}} + \frac{1}{m}\mathit{\boldsymbol{R}}_{\rm{w}}^{\rm{b}}\mathit{\boldsymbol{f}}_{{\rm{aero}}}^{\rm{w}} + \mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}{\mathit{\boldsymbol{g}}^{\rm{n}}} - } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right){\mathit{\boldsymbol{v}}^{\rm{b}}} + \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right)\mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}\mathit{\boldsymbol{v}}_{\rm{w}}^{\rm{n}}} \right] - {{\mathit{\boldsymbol{\dot u}}}_{{\rm{r,d}}}} - \nu d + \\ \;\;\;\;\;\;{k_{\rm{r}}}\left[ {{{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}1}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right) + {{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}2}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right)} \right]. \end{array} $ | (42) |
将式(33)代入式(42),得滑模控制律为
| $ \begin{array}{l} T = m\left\{ { - \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]\left[ {\frac{1}{m}\mathit{\boldsymbol{R}}_{\rm{w}}^{\rm{b}}\mathit{\boldsymbol{f}}_{{\rm{aero}}}^{\rm{w}} + \mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}{\mathit{\boldsymbol{g}}^{\rm{n}}} - } \right.} \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right){\mathit{\boldsymbol{v}}^{\rm{b}}} + {\rm{S}}\left( {\omega _{\rm{n}}^{\rm{b}}} \right)R_{\rm{n}}^{\rm{b}}v_{\rm{w}}^{\rm{n}}} \right] + {{\dot u}_{{\rm{r,d}}}} - \nu d - \\ \;\;\;\;\;\;{k_{{\rm{r1}}}}\frac{{{s_{\rm{r}}}}}{{{{\left\| {{s_{\rm{r}}}} \right\|}^{\frac{1}{2}}}}} - {k_{{\rm{r2}}}}{s_{\rm{r}}} + {{\tilde \omega }_{\rm{r}}} - \left[ {{{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}1}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right) + } \right.\\ \;\;\;\;\;\;\left. {\left. {{{\left| {{e_{\rm{r}}}} \right|}^{{\gamma _{{\rm{r}}2}}}}{\rm{sign}}\left( {{e_{\rm{r}}}} \right)} \right]} \right\}, \end{array} $ | (43) |
其中
考虑非线性系统(6)、(8)、(9),假设变
| $ {\mathit{\Theta }_\omega } = \frac{1}{2}\mathit{\boldsymbol{R}}~{\mathit{\boldsymbol{e}}_\omega }, $ |
| $ {\mathit{\Theta }_\tau } = {\mathit{\boldsymbol{J}}^{ - 1}}\left[ { - \mathit{\boldsymbol{S}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right)\mathit{\boldsymbol{J}}\left( {{\mathit{\boldsymbol{\omega }}_{\rm{e}}} + {\mathit{\boldsymbol{\omega }}_{\rm{d}}}} \right) - \mathit{\boldsymbol{J}}{{\mathit{\boldsymbol{\dot \omega }}}_{\rm{d}}} + {\mathit{\boldsymbol{e}}_\tau }} \right], $ |
| $ \begin{array}{l} {\mathit{\Theta }_T} = \frac{1}{m}{\left[ {\begin{array}{*{20}{c}} {{e_T}}&0&0 \end{array}} \right]^{\rm{T}}} + \frac{1}{m}\mathit{\boldsymbol{R}}_{\rm{w}}^{\rm{b}}\mathit{\boldsymbol{f}}_{{\rm{aero}}}^{\rm{w}} + \mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}{\mathit{\boldsymbol{g}}^{\rm{n}}} - \mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right){\mathit{\boldsymbol{v}}^{\rm{b}}} + \\ \;\;\;\;\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{\omega }}_{\rm{n}}^{\rm{b}}} \right)\mathit{\boldsymbol{R}}_{\rm{n}}^{\rm{b}}\mathit{\boldsymbol{v}}_{\rm{w}}^{\rm{n}}. \end{array} $ |
证明 定义eω=ωe-ωev;eτ=τ-τv;eT=T-Tv,其中τv为期望的气动力矩;Tv为期望的推力.把式(34)、(39)、(43)分别代入式(33)整理可得
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_i} = - {k_{i1}}\frac{{{\mathit{\boldsymbol{s}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}} - {k_{i2}}{s_i} + {{\mathit{\boldsymbol{\tilde \omega }}}_i} + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_j},\\ {{\mathit{\boldsymbol{\dot {\tilde \omega} }}}_i} = - {k_{i3}}\frac{{{\mathit{\boldsymbol{s}}_i}}}{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}} - {k_{i4}}{\mathit{\boldsymbol{s}}_i}. \end{array} \right. $ | (44) |
定义
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot s}}}_i} = - {k_{i1}}\frac{{{\mathit{\boldsymbol{s}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}} - {k_{i2}}{\mathit{\boldsymbol{s}}_i} + {\mathit{\boldsymbol{z}}_i},\\ {{\mathit{\boldsymbol{\dot z}}}_{\rm{i}}} = - {k_{i3}}\frac{{{\mathit{\boldsymbol{s}}_i}}}{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}} - {k_{i4}}{\mathit{\boldsymbol{s}}_i} + {\vartheta _j}. \end{array} \right. $ | (45) |
式中
定义李雅普诺夫方程为
| $ {V_s} = 2{k_{i3}}\left\| {{\mathit{\boldsymbol{s}}_i}} \right\| + {k_{i4}}{\mathit{\boldsymbol{s}}_i}^{\rm{T}}{\mathit{\boldsymbol{s}}_i} + \frac{1}{2}\mathit{\boldsymbol{z}}_i^{\rm{T}}{\mathit{\boldsymbol{z}}_i} + {\mathit{\boldsymbol{\zeta }}^{\rm{T}}}\mathit{\boldsymbol{\zeta }}. $ | (46) |
式中
对式(46)求微分,可得
| $ \begin{array}{l} \dot V = - \left( {{k_{i1}}{k_{i3}} + \frac{1}{2}k_{i1}^3} \right){\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^{\frac{1}{2}}} - \left( {{k_{i3}}{k_{i2}} + } \right.\\ \;\;\;\;\;\;\left. {2k_{i1}^2{k_{i2}}} \right)\left\| {{\mathit{\boldsymbol{s}}_i}} \right\| - {k_{i1}}\frac{{{\vartheta _j}^{\rm{T}}{\mathit{\boldsymbol{s}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}} - \\ \;\;\;\;\;\;\left( {{k_{i2}}{k_{i4}} + k_{i2}^3} \right){\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^2} - {k_{i2}}{\mathit{\boldsymbol{s}}_i}^{\rm{T}}{\vartheta _j} - \\ \;\;\;\;\;\;\left( {{k_{i1}}{k_{i4}} + \frac{5}{2}{k_{i1}}k_{i2}^2} \right){\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^{\frac{3}{2}}} + k_{i1}^2\frac{{{\mathit{\boldsymbol{s}}_i}^{\rm{T}}{\mathit{\boldsymbol{z}}_i}}}{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}} + \\ \;\;\;\;\;\;2k_{i2}^2{s_i}^T{z_i} + 3{k_{i1}}{k_{i2}}\frac{{{\mathit{\boldsymbol{s}}_i}^{\rm{T}}{\mathit{\boldsymbol{z}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}} - {k_{i2}}{\left\| {{\mathit{\boldsymbol{z}}_i}} \right\|^2} + \\ \;\;\;\;\;\;\frac{{{k_{i1}}}}{2}\frac{{\left( {{\mathit{\boldsymbol{s}}_i}^{\rm{T}}{\mathit{\boldsymbol{z}}_i}} \right)\left( {{\mathit{\boldsymbol{z}}_i}^{\rm{T}}{\mathit{\boldsymbol{s}}_i}} \right)}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{5}{2}}}}} - {k_{i1}}\frac{{{\mathit{\boldsymbol{z}}_i}^{\rm{T}}{\mathit{\boldsymbol{z}}_i}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}} + 2{\mathit{\boldsymbol{z}}_i}^{\rm{T}}{\vartheta _j}. \end{array} $ | (47) |
利用Cauchy-Schwarz不等式
| $ \begin{array}{l} \dot V \le - \left( {{k_{i1}}{k_{i3}} + \frac{1}{2}k_{i1}^3} \right){\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^{\frac{1}{2}}} - \\ \left( {{k_{i3}}{k_{i2}} + 2k_{i1}^2{k_{i2}}} \right)\left\| {{\mathit{\boldsymbol{s}}_i}} \right\| + 2{d_i}\left\| {{\mathit{\boldsymbol{z}}_i}} \right\| - \\ \left( {{k_{i1}}{k_{i4}} + \frac{5}{2}{k_{i1}}k_{i2}^2} \right){\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^{\frac{3}{2}}} + {k_{i2}}{d_i}\left\| {{\mathit{\boldsymbol{s}}_i}} \right\| + \\ k_{i1}^2\left\| {{\mathit{\boldsymbol{z}}_i}} \right\| - \left( {{k_{i2}}{k_{i4}} + k_{i2}^3} \right){\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^2} + \\ 2k_{i2}^2\left\| {{\mathit{\boldsymbol{s}}_i}} \right\| \cdot \left\| {{\mathit{\boldsymbol{z}}_i}} \right\| + 3{k_{i1}}{k_{i2}}{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^{\frac{1}{2}}}\left\| {{\mathit{\boldsymbol{z}}_i}} \right\| - \\ {k_{i2}}{\left\| {{\mathit{\boldsymbol{z}}_i}} \right\|^2} + \frac{{{k_{i1}}}}{2}\frac{{{{\left\| {{\mathit{\boldsymbol{z}}_i}} \right\|}^2}}}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}} + {k_{i1}}{d_i}{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|^{\frac{1}{2}}}. \end{array} $ | (48) |
定义
| $ \dot V = - \frac{1}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}}{\mathit{\boldsymbol{o}}^{\rm{T}}}\mathit{\boldsymbol{Po}} - {\mathit{\boldsymbol{o}}^{\rm{T}}}\mathit{\boldsymbol{Qo}}. $ | (49) |
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {{k_{i2}}\left( {{k_{i3}} - {d_i}} \right) + 2k_{i1}^2{k_{i2}}}&0&0\\ 0&{{k_{i2}}{k_{i4}} + k_{i2}^3}&{ - k_{i2}^2}\\ 0&{ - k_{i2}^2}&{{k_{i2}}} \end{array}} \right], $ |
| $ \begin{array}{l} \mathit{\boldsymbol{P}} = \\ \left[ {\begin{array}{*{20}{c}} {\frac{1}{2}k_{i1}^3 + {k_{i1}}\left( {{k_{i3}} - {d_i}} \right)}&0&{ - \frac{1}{2}k_{i1}^2 - {d_i}}\\ 0&{{k_{i1}}{k_{i4}} + \frac{5}{2}{k_{i1}}k_{i2}^2}&{ - \frac{3}{2}{k_{i1}}{k_{i2}} - }\\ {\frac{1}{2}k_{i1}^2 - {d_i}}&{ - \frac{3}{2}{k_{i1}}{k_{i2}}}&{\frac{1}{2}{k_{i1}}} \end{array}} \right]. \end{array} $ |
如果参数满足
| $ {k_{i1}} > \sqrt 2 {d_i},\;\;\;\;{k_{i2}} > 0, $ |
| $ {k_{i3}} > \max \left\{ {3{d_i} + \frac{{2d_i^2}}{{k_{i1}^2}},\frac{{ - 2k_{i1}^2{k_{i2}} + {k_{i2}}{d_i}}}{{{k_{i2}}}}} \right\}, $ |
| $ {k_{i4}} > \frac{{{{\left( {3k_{i1}^2{k_{i2}} + 6{k_{i2}}{d_i}} \right)}^2}}}{{k_{i1}^2{k_{i3}} - 2d_i^2 - 3k_{i1}^3{d_i}}} + 2k_{i2}^2, $ |
可以得到Q>0, P>0,从而式(49)可以重写为
| $ \dot V = - \frac{1}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}}{\mathit{\boldsymbol{o}}^{\rm{T}}}\mathit{\boldsymbol{Po}} \le - \frac{1}{{{{\left\| {{\mathit{\boldsymbol{s}}_i}} \right\|}^{\frac{1}{2}}}}}{\lambda _{\min }}\left( \mathit{\boldsymbol{P}} \right){\left\| \mathit{\boldsymbol{o}} \right\|^2}. $ |
定义
| $ \mathit{\boldsymbol{R}} = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} {4{k_{i3}} + k_{i1}^2}&{{k_{i1}}{k_{i2}}}&{ - {k_{i1}}}\\ {{k_{i1}}{k_{i2}}}&{2{k_{i4}} + k_{i2}^2}&{ - {k_{i2}}}\\ { - {k_{i1}}}&{ - {k_{i2}}}&2 \end{array}} \right]. $ |
可以得到
| $ \dot V \le - g{V^{\frac{1}{2}}}, $ | (50) |
式中
选择合适的参数ki1, ..., ki4,滑模面si及其导数
| $ {t_s} \le \frac{{2{V^{\frac{1}{2}}}\left( 0 \right)}}{g}. $ | (51) |
为了验证本文所提出方法的正确性,对无人机模型式(6)、(8)、(9)作为被控对象进行仿真.无人机详细参数选自文献[14], 在此简述该无人机的一些关键参数为
| $ \bar c = 0.76\;{\rm{m}},b = 1.37\;{{\rm{m}}^2},m = 20.64\;{\rm{kg}}, $ |
| $ {I_{xx}} = 1.607\;3\;{\rm{kg/}}{{\rm{m}}^2},{I_{yy}} = 7.5085\;{\rm{kg/}}{{\rm{m}}^2}, $ |
| $ {I_{zz}} = 7.186\;5\;{\rm{kg/}}{{\rm{m}}^2},{J_{xz}} = - 0.561\;44\;{\rm{kg/}}{{\rm{m}}^2}. $ |
自适应干扰观测器与超螺旋滑模控制器参数为
ω1=20, γ1=4, ε1=4, kq=0.5, kq1=0.2, kq2=0.1, kq3=0.01, kq4=0.025, γq1=1, γq2=0.5, kω=5, kω1=3.5, kω2=2, kω3=0.5, kω4=0.2, γω1=1, γω2=0.5, kr=3, kr1=1.5, kr2=1;kr3=0.2;kr4=0.1, γr1=1, γr2=0.5.
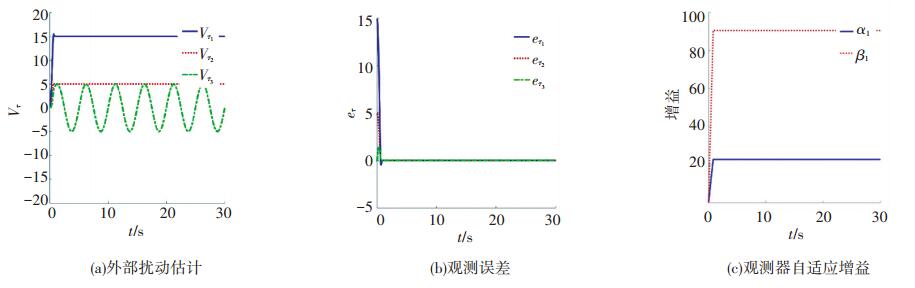
自适应滑模干扰观测器阈值δT=10-3,初始角速度ωnb=[0.2 0.1 0.3]T, 期望角速度ωd=[0 0 0.5]T, 单位:rad/s;初始四元数选取qd, b=[0.8 0.346-0.346 0.346]T,期望四元数qd=[1 0 0 0]T;初始速度10 m/s,期望速度分别为30 m/s及(10+t)m/s.在飞行过程中对固定翼无人机模型施加外界扰动,其中转动环节施加的外界扰动Δτ=[15 5 5sin(2πt/5)]T,平动环节施加的外部扰动Δd=[6sin(3πt/5) 0 0]T,仿真效果如图 3~8所示.
|
图 3 干扰观测器估计转动环节外部扰动,观测误差及增益 Figure 3 The disturbance of rotation, observation error and adaptive gains under disturbance observer |
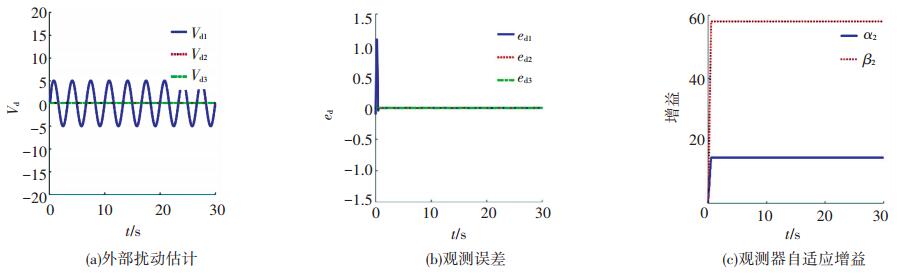
|
图 4 干扰观测器估计平动环节外部扰动,观测误差及增益 Figure 4 The disturbance of translation, observation error and adaptive gains under disturbance observer |
|
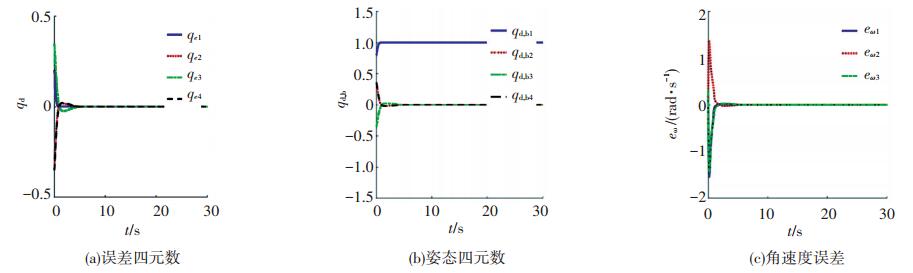
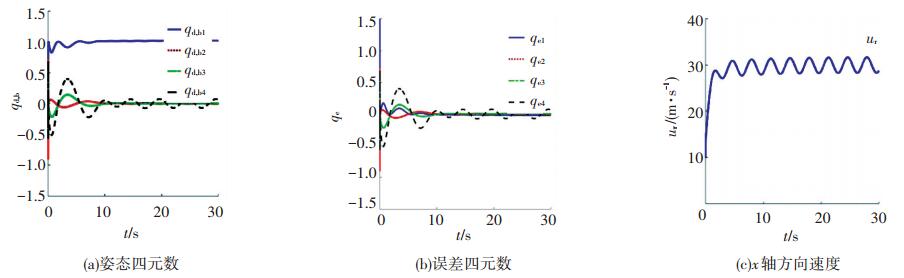
图 5 姿态误差四元数、姿态四元数、角速度误差曲线 Figure 5 Curve of quaternion attitude error, quaternion attitude and angular velocity error |
|
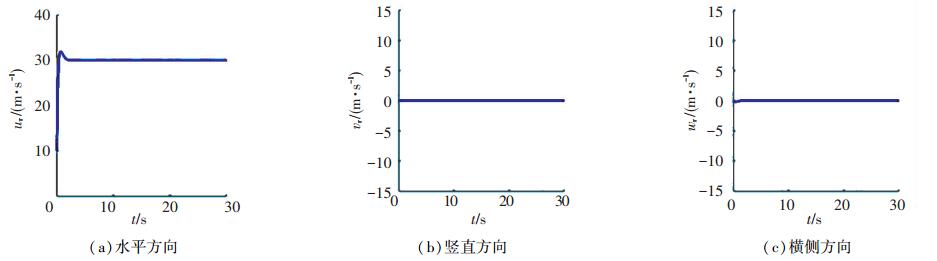
图 6 无人机平飞速度曲线 Figure 6 Speed curve of UAV in level flight |
|
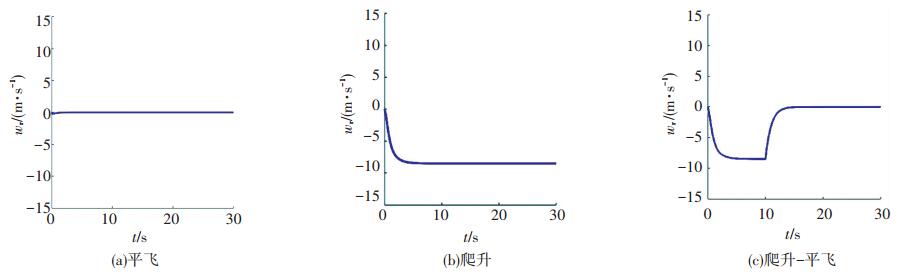
图 7 无人机平飞、爬升、爬升-平飞阶段沿z轴方向速度曲线 Figure 7 Speed curve of UAV in level, climbing, climbing to level flight along the z-axis |
|
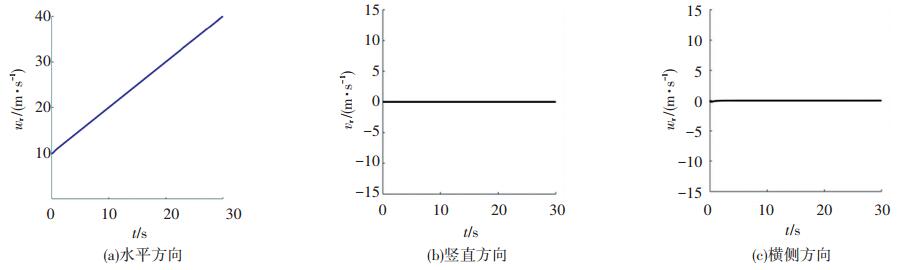
图 8 无人机加速度平飞速度曲线 Figure 8 Speed curve of UAV in accelerated flight |
由图 3、4可以看出,自适应滑模干扰观测器精确迅速的观测外部扰动,估计误差在很短的时间内达到平衡点附近.在超螺旋滑模控制律的作用下,无人机的姿态和角速度很快收敛到期望值如图 5所示.由图 5(a)中姿态四元数跟踪误差曲线和图 5(b)中姿态四元数跟踪曲线可以看出,固定翼无人机姿态在2 s左右达到期望指令,并且相对于传统的滑模控制,抖震现象减弱,但没有完全消除,这是滑模控制器固有的缺陷.由图 5(c)可以看出,姿态角速度误差在很短时间内收敛到零,虽然在稳定阶段存在微小抖震现象,但是总体控制幅度小于1.5 rad/s,该控制律满足实际工程中的需求.
无人机速度控制效果如图 6~8所示,从图中可以看出超螺旋滑模控制算法可以精确地、有效的跟踪期望指令.其中图 7水平速度跟踪指令为常值,改变攻角α,可以得到不同的纵向飞行状态,从图 8中可以看出,控制策略对无人机加速度飞行也有良好的控制效果,无人机速度能精确的跟踪上期望加速度指令.
为了验证该综合控制策略的有效性,故在同等条件下进行一组PID控制仿真实验,如图 9所示.从图中可以明显看出,PID控制器不能让带扰动的固定翼无人机姿态和速度收敛到期望指令.从而反映了本文所提出的综合控制策略对扰动有着很好的抑制作用,并且能精确快速的跟踪预期指令.
|
图 9 PID控制下的姿态与速度曲线 Figure 9 UAV attitude and the speed curve by PID |
1) 主要研究了固定翼无人机的速度和姿态在外界干扰及不确定影响下的控制问题.针对无人机在飞行环境下存在不确定和外部干扰的情况,提出了自适应多变量干扰观测器,对外部干扰进行有限时间精确估计.
2) 结合多变量超螺旋滑模控制器,设计了一种综合控制策略对固定翼无人机速度和姿态进行控制,不仅有效地解决了模型中不确定和干扰的估计问题还对无人机的期望指令进行了精确的跟踪.
3) 通过对固定翼无人机不同飞行状态的仿真验证,得出设计的综合控制策略在不确定及外界扰动的综合影响的情况下能够实现对固定翼无人机的姿态与速度指令的快速稳定跟踪.
| [1] |
EFE M Ö. Neural network assisted computationally simple PID control of a quadrotor UAV[J]. IEEE Transactions on Industrial Informatics, 2011, 7(2): 354. DOI:10.1109/TII.2011.2123906 |
| [2] |
JUNG D, TSIOTRAS P. Bank-to-turn control for a small UAV using backstepping and parameter adaptation[J]. IFAC Proceedings Volumes, 2008, 41(2): 4406. DOI:10.3182/20080706-5-KR-1001.00742 |
| [3] |
NICOL C, MACNAB C, RAMIREZ S. Robust adaptive control of a quadrotor helicopter[J]. Mechatronics, 2011, 21(6): 927. DOI:10.1016/j.mechatronics.2011.02.007 |
| [4] |
DUCARD G, HANS P G. Stability analysis of a dynamic inversion based pitch rate controller for an unmanned aircraft[C]//IEEE International Conference on Intelligent Robots and Systems.France, NJ: IEEE Press, 2008: 360. DOI: 10.1109/IROS.2008.4651117
|
| [5] |
TAYEBI A. Unit quaternion-based output feedback for the attitude tracking problem[J]. IEEE Transactions on Automatic Control, 2008, 53(6): 1516. DOI:10.1109/TAC.2008.927789 |
| [6] |
费爱玲, 李柠, 李少远. 固定翼无人机的自抗扰反步控制[J]. 控制理论与应用, 2016, 33(10): 1296. FEI Ailing, LI Ning, LI Shaoyuan. Active disturbance rejection back-stepping control of fixed-wing unmanned aerial vehicle[J]. Control Theory & Applications, 2016, 33(10): 1296. |
| [7] |
EDWARDS C, SPURGEON S K. Sliding mode control: theory and applications[M]. [S.l.]: Crc Press, 1998.
|
| [8] |
BRANDTSTADTET H. Sliding mode control of electromechanical systems[J]. Control Engineering Practice, 2000, 38: 586. |
| [9] |
DONG Qi, ZONG Qun, TIAN Bailing, et al. Adaptive disturbance observer-based finite-time continuous fault-tolerant control for reentry RLV[J]. International Journal of Robust & Nonlinear Control, 2017, 27(18): 4275. DOI:10.1002/rnc.3796 |
| [10] |
DONG Qi, ZONG Qun, TIAN Bailing, et al. Adaptive-gain multivariable super-twisting sliding mode control for reentry RLV with torque perturbation[J]. International Journal of Robust & Nonlinear Control, 2016, 27(4): 620. DOI:10.1002/rnc.3589 |
| [11] |
DONG Qi, ZONG Qun, TIAN Bailing, et al. Integrated finite-time disturbance observer and controller design for reusable launch vehicle in reentry phase[J]. Journal of Aerospace Engineering, 2017, 30(1): 04016076. DOI:10.1061/(ASCE)AS.1943-5525.0000670 |
| [12] |
ZONG Qun, DONG Qi, WANG Fang, et al. Super twisting sliding mode control for a flexible air-breathing hypersonic vehicle based on disturbance observer[J]. Science China Information Sciences, 2015, 58(7): 1. DOI:10.1007/s11432-015-5350-6 |
| [13] |
穆朝絮, 孙长银, 钱承山. 基于干扰观测器的卫星姿态误差四元数模糊滑模控制[J]. 东南大学学报(自然科学版), 2012, 42(5): 886. MU Chaoxu, SUN Changyin, QIAN Chengshan. Error quaternion fuzzy sliding mode control of attitude for spacecraft based on disturbance observer[J]. Journal of Southeast University(Natural Science Edition), 2012, 42(5): 886. |
| [14] |
PHILLIPS K, CAMPA G, GURURAJAN S, et al. Parameter identification for application within a fault-tolerant flight control system[C]//2009 AIAA Atmospheric Flight Mechanics Conference. Chicago, NJ: AIAA, 2009: 5723. DOI10.2514/6.2009-5723
|
 2018, Vol. 50
2018, Vol. 50


